扩展功能
文章信息
- 覃文文
- QIN Wen-wen
- 基于部分随机用户均衡的可变信息板选址双层规划模型
- A Bi-level Programming Model for Variable Message Signs Locating Based on Partial Stochastic User Equilibrium
- 公路交通科技, 2016, 33(11): 126-133
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 126-133
- 10.3969/j.issn.1002-0268.2016.11.019
-
文章历史
- 收稿日期: 2015-12-30
VMS作为一种群体式的交通流诱导信息发布系统,其布局和信息发布对出行质量起着关键性的影响,合理布设VMS具有重要意义[1]。目前,VMS诱导下的路径选择行为一直是学术界广泛关注的热点。钟石泉等[2]研究了图形VMS发布路况信息下不同因素对驾驶员诱导服从行为的影响。徐天东等[3]基于实时交通数据,利用经验分析法与probit模型量化了不同VMS信息内容对驾驶员在途转移行为的影响。尚华艳等[4]采用元胞传输模型分析了路径选择概率变化与VMS位置之间的关系。姜桂艳等[5]应用仿真模拟方法,探讨了拥挤条件下VMS发布诱导信息对驾驶行为的影响。上述研究多为VMS布局已知,在小范围路网内对VMS诱导下的路径选择行为进行建模仿真,较少关注VMS选址问题,特别是考虑交通系统对VMS选址建模的不确定性影响。Chiu等[6]假定所有出行者拥有完全信息,能预期其他出行者路径选择行为,建立了上层为最大化信息发布收益的VMS最优布点、下层为用户动态最优的交通分配模型。该模型涉及多个VMS候选方案的评估,计算量过大,难以应用于大规模城市路网。随后,Chiu等[7]进一步考虑了随机事故与ATIS共存情况下的动态VMS最优选址问题,发现同时部署VMS与ATIS比相继安装两个系统效益更好。上述研究主要考虑突发事故影响下的VMS布局优化,考虑因素较为单一,未能将交通系统的不确定性作为一个整体纳入VMS选址模型中,以更好地切合实际情况。
综上分析,VMS选址方案是在一个不确定性的路网环境中进行VMS的最佳布局,而这种不确定性主要体现在:(1)交通需求的不确定性,即用户出行的随机性;(2)道路交通状态的不确定性,如路段突发交通事故等;(3)认知的不确定性,即VMS信息发布的不完全和出行者对信息的认知偏差,导致出行者做出违背信息诱导的路径选择行为。本文从以上3个层面,引入信息论中熵的概念,通过部署VMS,以信息熵衡量VMS消除影响区域内的不确定性程度,使用行程时间的期望和标准差量化不确定决策中的风险,基于部分随机用户平衡描述VMS诱导下的出行者路径选择行为,建立VMS选址规划模型,并设计模型的求解算法。
1 问题描述在整个路网中,只有VMS影响的区域为信息透明的区域,出行者能够通过VMS发布的信息准确了解前方局部路网的交通状况,并决定是否响应VMS的信息诱导,做出符合自身利益的路径选择。可在Logit模型的基础上,建立VMS诱导下的出行者信息响应模型来描述诱导服从率对于出行者路径选择行为的影响。而在VMS影响之外的区域路网,则为没有信息指引的区域,出行者只能根据行车经验、习惯性等因素进行路径选择,此时,可采用Logit模型来描述路网上的随机行为。
2 模型构建考虑一个不确定路网环境的交通网络G=(N, A),其中, N为所有节点的集合;A为所有路段的集合;A为所有VMS影响路段的集合;(i, j)为网络中的有向路段,(i, j)∈A,i,j∈N;R为所有起点的集合,r∈R;S为所有终点的集合,r∈R;Krs为OD对r-s之间有效路径的集合,k∈Krs;Ω为OD需求与路段通行能力随机抽样形成的不确定情景集合;ω为Ω集合中任一需求与供给情景的实现;qrsω为ω情景下OD对r-s之间的OD需求量;pω为ω情景发生概率;xijω为ω情景下路段(i, j)的流量;tijω(xijω)为ω情景下路段(i, j)所需的行程时间,假设其只与该路段上的流量和实际通行能力有关;ck, rsω为ω情景下OD对r-s之间路径k的阻抗;δij, krs为路径与路段流量关系的布尔变量,若路段(i, j)在OD对r-s之间路径k上,其值为1,否则为0;fk, rsω为ω情景下的OD对r-s之间路径k的流量。
其中,假定OD需求服从截尾正态分布Q~TN (qrs, γqrs),qrs为OD对r-s之间的需求均值,γ为需求抽样的扰动因子;路段通行能力Cij服从均匀分布Cij~(φijCij, Cij),Cij为路段(i, j)的通行能力上界,φij为路段(i, j)的通行能力受到交通事故、道路维护等外界因素影响的下降水平系数,φij∈[0,1]。
2.2 信息熵的估计研究表明,VMS的收益不仅体现在缩短行程时间上,对减少交通状况的不确定性也有突出贡献[8]。因此,考虑到城市交通网络处于一个随机干扰环境中,路段的交通状态具有不确定性与实时性,本文将利用信息熵衡量影响区域内VMS消除的不确定性程度,即局部路网产生的信息熵越大,越需要部署VMS消除路段交通状态的不确定性。基于以上思路,定义VMS覆盖的路段为有效影响路段,VMS影响区域信息熵的估计公式为:
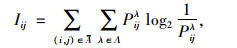
|
(1) |
式中,Iij为路段(i, j)上的VMS所覆盖区域产生的信息熵;Pijλ为有效影响路段(i, j)上λ情景发生的概率。
考虑4种路段交通情景的集合Λ={λ1=顺畅(V/C≤0.6);λ2=稍有拥堵(0.6 < V/C≤0.8);λ3=拥堵(0.8 < V/C≤1);λ4=严重拥堵(V/C > 1)}。其中,V为路段流量;C为路段通行能力。估计任一交通情景的发生概率pλ的基本步骤是:
Step 1:初始化。确定OD需求概率分布函数和路段通行能力概率分布函数。
Step 2:令抽样次数t=1。
Step 3:随机生成本轮OD需求量和路段通行能力值。
Step 4:采用随机用户平衡配流模型,将交通量加载到路网上,获得有效影响路段(i, j)的V/C比值hijt。
Step 5:如果hijt∈(0, 0.6],则λij1=λij1+1;如果hijt∈(0.6, 0.8],则λij2=λij2+1;如果hijt∈(0.8, 1],则λij3=λij3+1;如果hijt∈(1, +∞],则λij4=λij4+1。
Step 6:如果t小于抽样规模T,则t=t+1;返回Step 3。
Step 7:如果t=T,则停止,计算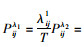
文献[9-10]以诱导交通量最大化为目标研究了VMS选址问题,但未能将VMS诱导下的路径选择行为纳入选址模型中进行集成分析,这就使得选址方案与出行者之间缺乏反馈机制。交通管理者做出选址方案决策,其结果能够影响并引导交通流分布到交通负荷水平较低的道路,但不能直接决定路网中的出行者都服从信息诱导;反过来,出行者可选择是否对VMS发布的信息做出响应,改变自己原有的出行路径,这将直接关系到VMS选址方案的实施能否获得良好的收益,并对交通管理者的决策产生一定影响。因此,VMS选址模型的建立要考虑出行者的诱导服从行为。
根据上述讨论,设u为VMS影响区域内出行的起点,V为VMS影响区域内出行终点的集合,Kuv为起点u与讫点v之间的路径集合。在VMS影响区域建立出行者信息响应模型,引入诱导服从率E∈[0,1]来表征出行者信息响应特性,E为0或1时表示所有出行者都会忽略或服从VMS的信息诱导。具体模型如下:
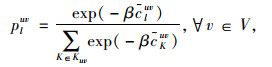
|
(2) |
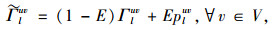
|
(3) |
式中,pluv为起点u与讫点v之间出行者服从信息诱导后选择路径l的概率;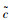
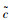
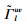
VMS选址方案的决策过程是典型的领导者-跟随者双层规划问题,交通管理者对城市路网部署VMS后,驾驶员根据VMS发布的前方路况信息,结合自身经验与利益,选择出行路径。在VMS选址的双层规划模型中,上层模型从领导者的角度出发,提出布局方案,下层模型从跟随者的角度出发,调整出行行为;上层模型再根据下层模型反馈的信息,做出符合全局最优的决策,模型结构见图 1。
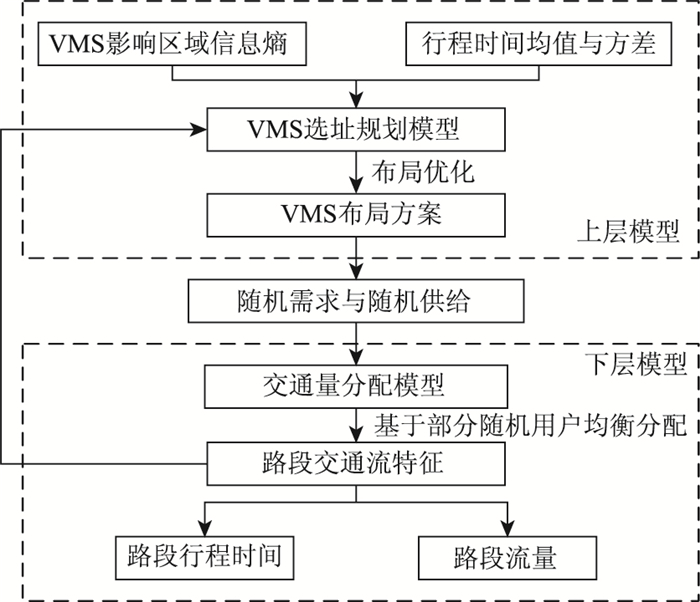
|
| 图 1 模型结构 Fig. 1 Model structure |
| |
2.4.1 上层模型
考虑到随机需求强度和随机通行能力下降对VMS选址结果造成的较大差异,决策者也将面临很大的决策风险。为了降低选址方案对不确定性的敏感度,采用行程时间的期望和标准差量化不确定决策中的风险,希望模型处理不确定性的风险值最小,以提高模型鲁棒性。上层模型包含两个目标函数:一个是最小化VMS影响区域产生的信息熵;另一个是最小化所有需求与供给情景发生下的路网总行程时间均值和标准差。具体模型如下。
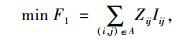
|
(4) |
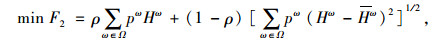
|
(5) |
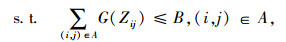
|
(6) |
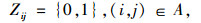
|
(7) |
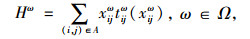
|
(8) |
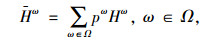
|
(9) |
式中, ρ(0≤ρ≤1)为权重因子;Hω为需求和供给情景ω时的路网总行程时间;Hω为路网总行程时间的期望值;G(Zij)为路段(i, j)配置VMS的投资函数;B为整个路网配置VMS的预算总额;Zij是0-1变量,当路段(i, j)设置有VMS时,Zij=1,反之,Zij=1。
2.4.2 下层模型下层模型为部分随机用户均衡模型[12]。在VMS影响区域内,部分随机用户均衡是指服从信息诱导的出行者能够调整原有路径选择行为,其他出行者则保持原有的路径选择行为,实现新的随机用户均衡;而VMS影响区域之外,则仍然遵循基于Logit的随机用户均衡模型[12]。具体模型如下。
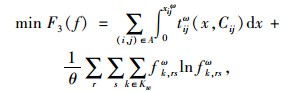
|
(10) |
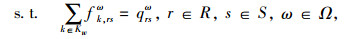
|
(11) |
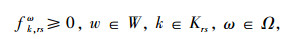
|
(12) |
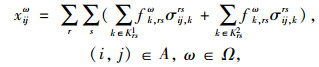
|
(13) |
式中,tijω(x, Cij)为ω情景下关于流量x和路段(i, j)通行能力的行程时间函数;θ为模型参数;Krs1为进行VMS诱导时路径流量经过VMS所在路段的路径集,显然有Krs1⊆Krs,从而未经过VMS所在路段的路径集为Krs2=Krs-Krs1。
3 模型求解算法针对多目标优化的VMS选址问题,最佳方法是求得问题的Pareto解集,然后根据决策人的偏好程度从Pareto解集中选择其中一组解作为解决方案[13]。因此,采用基于Monte Carlo模拟的NSGA-Ⅱ算法[13]求解双层规划模型,对于下层模型,首先根据文献[15]确定交通网络中任意OD对之间的有效路径集,然后基于Dial算法的基本框架,设计考虑VMS诱导的流量加载算法,并将此算法嵌入相继平均法(Method of Successive Averages, MSA)中,用于求解下层模型的随机交通分配问题。
3.1 下层模型求解 3.1.1 VMS诱导下的流量加载算法原有的Dial算法需要进行起讫点间的正反两次最短路径搜索,计算过程较为复杂。因此,基于Dial算法的基本框架,设计了能反映VMS诱导下的出行者路径选择行为的流量加载算法。定义s(·)为相应节点到终点s的最小阻抗,具体算法过程如下。
Step 1:初始化。对OD对r-s之间属于有效路径的路段进行标号处理,用lij=1表示;lij=0则表示该路段不属于有效路径的路段。
Step 2:对于每个路段(i, j),按式(14)计算路段似然值,其中tij为路段(i, j)的行程时间。
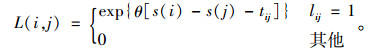
|
(14) |
Step 3:从终点s开始逆序计算路段权重W(i, j),当j到达起点r时,停止权重计算。其中定义downi为路段起点为i的路段终点集合(即为i所有的下游节点集合),具体计算公式为:
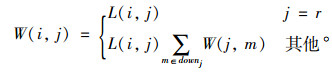
|
(15) |
Step 4:从起点r开始顺序计算i节点到下游各相邻节点j选择路段(i, j)的概率P(i, j):
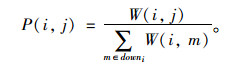
|
(16) |
Step 5:正向加载路段流量。对OD起点r,将qrsω分配到有效路径组成的网络上,其中定义upi为路段终点为i的路段起点集合(即为i所有的上游节点集合),有:
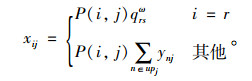
|
(17) |
Step 6:VMS影响区域内的流量加载。采用式(2)~(3)对VMS影响区域内的路段流量进行重新分配。且有:
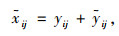
|
(18) |
式中,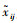
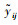
不难看出,上述算法首先实现的是正向路段流量加载的Dial算法,之后在VMS影响区域内嵌入出行者信息响应模型,重新调整影响区域内的流量,从而真正实现了静态网络中考虑VMS诱导的出行者路径选择行为的流量加载算法。
3.1.2 VMS诱导下的MSA算法为了求解考虑拥挤效应的用户均衡随机配流问题,可运用MSA算法实现路段出行时间为随机变量的交通分配。算法的具体步骤如下。
Step 1:初始化。基于自由流行程时间{tij(0)},利用3.1.1中描述的加载算法执行一次流量分配,产生路段的初始交通量{xijω, 1},令迭代次数n=1。
Step 2:更新路段行程时间tijω, n=tij(xijω, n-1), ∀i, j。
Step 3:寻找迭代方向。在现有路段行程时间{tijω, n}的基础上,利用3.1.1中所述算法执行一次流量加载,得到新的路段流量{zijω, n}。
Step 4:计算各路段的交通量:
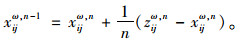
|
(19) |
Step 5:收敛性检查。若满足式(20)的收敛准则,算法终止,其中ε为预先给定的收敛精度参数;否则令n=n+1,并转至Step 2。
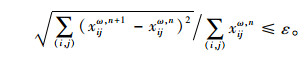
|
(20) |
由资金约束条件(6)生成VMS初始可行解集,代入部分随机用户均衡配流模型中,根据所有OD随机需求和路段随机供给的交通分配结果计算上层规划的目标函数,得到种群中每个个体(VMS选址方案)的适应度,并进行选择、交叉、变异及非支配排序等步骤,最终获得VMS选址问题的Pareto最优解集。算法流程如图 2所示。
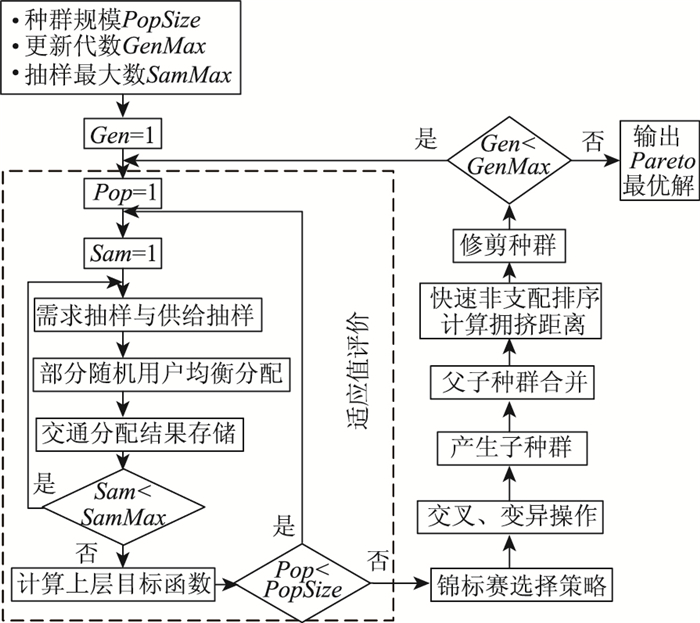
|
| 图 2 基于Monte Carlo的NSGA-Ⅱ算法流程图 Fig. 2 Flowchart of NSGA-Ⅱ algorithm based on Monte Carlo |
| |
4 算例分析
以图 3所示的简单路网为例,对上述模型及求解算法进行验证。假设VMS候选集合V={ V2, V5, V15, V20, V29, V34},V2的有效影响路段为{15, 16, 17, 18, 19},V5的有效影响路段为{20, 21, 22, 37, 38, 39},V15的有效影响路段为{17, 18, 19, 20, 21, 22},V20的有效影响路段为{23, 24, 25, 26, 27},V29的有效影响路段为{31, 32, 33, 34, 35, 36},V34的有效影响路段为{37, 38, 39, 40, 41}。表 1为简单路网的相关参数,包括路段自由流行程时间、通行能力上限。
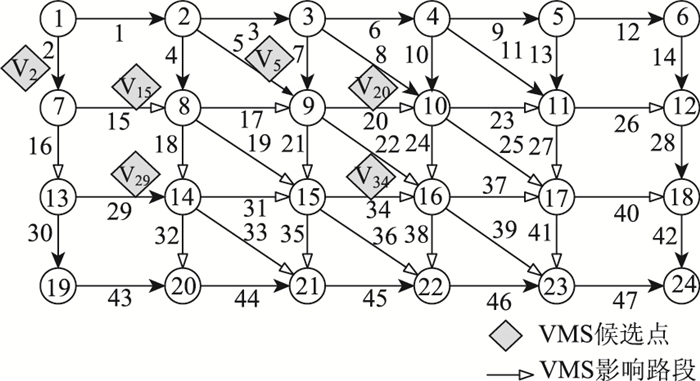
|
| 图 3 简单路网 Fig. 3 Simple road network |
| |
| 路段 | 节点顺序 | 自由流行程时间/h | 通行能力上限/ (veh·h-1) |
| 1 | 1→2 | 0.05 | 1 000 |
| 2 | 1→7 | 0.04 | 1 000 |
| 3 | 2→3 | 0.05 | 800 |
| 4 | 2→8 | 0.04 | 700 |
| 5 | 2→9 | 0.06 | 600 |
| 6 | 3→4 | 0.05 | 700 |
| 7 | 3→9 | 0.04 | 500 |
| 8 | 3→10 | 0.06 | 300 |
| 9 | 4→5 | 0.05 | 200 |
| 10 | 4→10 | 0.04 | 500 |
| 11 | 4→11 | 0.06 | 200 |
| 12 | 5→6 | 0.05 | 900 |
| 13 | 5→11 | 0.04 | 200 |
| 14 | 6→12 | 0.04 | 700 |
| 15 | 7→8 | 0.05 | 400 |
| 16 | 7→13 | 0.04 | 200 |
| 17 | 8→9 | 0.05 | 300 |
| 18 | 8→14 | 0.04 | 500 |
| 19 | 8→15 | 0.06 | 300 |
| 20 | 9→10 | 0.05 | 800 |
| 21 | 9→15 | 0.04 | 500 |
| 22 | 9→16 | 0.05 | 200 |
| 23 | 10→11 | 0.05 | 200 |
| 24 | 10→16 | 0.04 | 500 |
| 25 | 10→17 | 0.06 | 300 |
| 26 | 11→12 | 0.05 | 800 |
| 27 | 11→17 | 0.04 | 200 |
| 28 | 12→18 | 0.04 | 800 |
| 29 | 13→14 | 0.05 | 800 |
| 30 | 13→19 | 0.04 | 700 |
| 31 | 14→15 | 0.05 | 200 |
| 32 | 14→20 | 0.04 | 500 |
| 33 | 14→21 | 0.06 | 300 |
| 34 | 15→16 | 0.05 | 600 |
| 35 | 15→21 | 0.04 | 500 |
| 36 | 15→22 | 0.06 | 300 |
| 37 | 16→17 | 0.05 | 400 |
| 38 | 16→22 | 0.04 | 500 |
| 39 | 16→23 | 0.06 | 500 |
| 40 | 17→18 | 0.05 | 800 |
| 41 | 17→23 | 0.04 | 500 |
| 42 | 18→24 | 0.04 | 500 |
| 43 | 19→20 | 0.05 | 600 |
| 44 | 20→21 | 0.05 | 700 |
| 45 | 21→22 | 0.05 | 800 |
| 46 | 22→23 | 0.05 | 900 |
| 47 | 23→24 | 0.05 | 1 000 |
4.1 模型参数
假设VMS投资函数为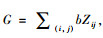
已有研究表明有限的小样本也能产生近似于最优的解[16],因此,本文设定抽样规模为50次,需求均值q1,24=1 500 veh/h,需求抽样扰动因子γ=0.3,各路段下降水平系数均为φij=0.7。
4.2 计算结果分析应用NSGA-Ⅱ算法求出参数ρ=0.8,θ=0.01,β=0.1,诱导服从率E为不同值时的Pareto最优VMS选址解集及对应的路网总行程时间的期望值(Expected Total Travel Time, ETTT),如表 2所示。
| 参数组合 | ρ=0.8,θ=0.01,β=0.1,E=0.4 | ρ=0.8,θ=0.01,β=0.1,E=0.6 | ρ=0.8,θ=0.01,β=0.1,E=0.8 | ρ=0.8,θ=0.01,β=0.1,E=0.1 | |||||||||||||||||
| 个体序号 | A | B | C | D | E | A | B | C | D | E | A | B | C | D | E | A | B | C | D | E | |
| 选址方案 | V2, V29 | V20, V29 | V2, V29, V34 | V29, V34 | V15, V34 | V20, V29 | V2, V29 | V2, V29, V34 | V29, V34 | V20, V29 | V2, V29 | V2, V20 | V2, V29, V34 | V2, V34 | V15, V34 | V2, V15, V34 | V20, V29 | V29, V34 | |||
| 目标值 | F1 | 10.999 | 9.142 | 18.580 | 10.925 | 14.847 | 9.241 | 11.179 | 17.317 | 9.859 | 9.316 | 10.792 | 14.304 | 18.261 | 15.645 | 15.698 | 22.420 | 9.814 | 10.030 | ||
| F2 | 1.023 | 1.064 | 1.009 | 1.052 | 0.998 | 1.082 | 1.023 | 0.994 | 1.058 | 1.046 | 1.038 | 1.027 | 1.012 | 1.024 | 1.028 | 1.012 | 1.118 | 1.030 | |||
| ETTT | 0.528 | 0.497 | 0.503 | 0.503 | 0.494 | 0.505 | 0.503 | 0.511 | 0.498 | 0.513 | 0.518 | 0.514 | 0.486 | 0.506 | 0.553 | 0.514 | 0.510 | 0.488 | |||
对表 2进行初步分析,发现有些选址方案(如V2, V29和V20, V29)在不同参数组合的随机情景下都被选中,这是由于在随机需求与随机供给条件下,本文模型很好地降低出行环境的动态变化给选址带来的敏感性影响,得到稳健性VMS选址方案,决策者可综合考虑VMS建设、运营与维护成本等因素,在规划实践中将路段2,20,29作为规划方案的重点选择对象部署VMS。
为了进一步分析诱导服从率E对路网运行质量的影响,图 2显示了E取不同值时的VMS最优解集分布。不难发现,当E值增大到0.6时,不同E取值下的Pareto前沿面整体都在往下移动,分布在Pareto前沿面上的个体ETTT值呈下降趋势,这可以解释为交通网络中部署的VMS发挥了诱导作用,随着出行者对VMS发布信息服从程度的逐步上升,有效地降低了整体网络的ETTT值。而随着E值的进一步增大,Pareto前沿面整体往上移动,ETTT值有上升趋势,此时,过多的出行者接受VMS诱导,极易形成集聚反应,将会恶化交通网络的运行状况。
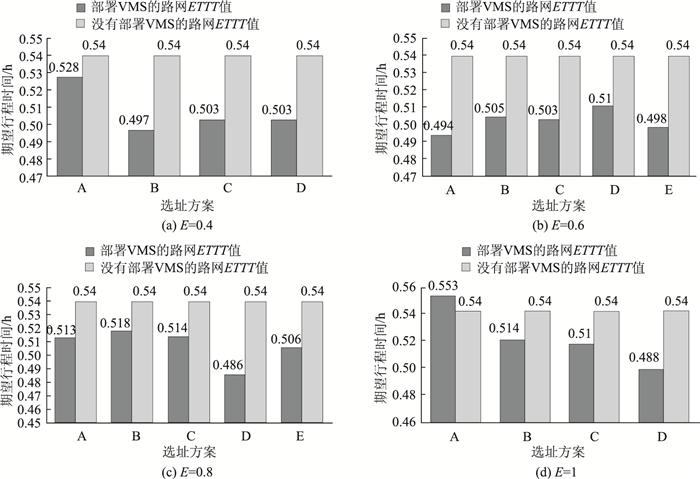
图 4显示了不同E值的选址方案ETTT值与没有部署VMS的路网ETTT值的比较情况。其中,在没有部署VMS的路网中,考虑了相同抽样条件的随机需求与随机供给情景下求解得到的ETTT值为0.54 h。
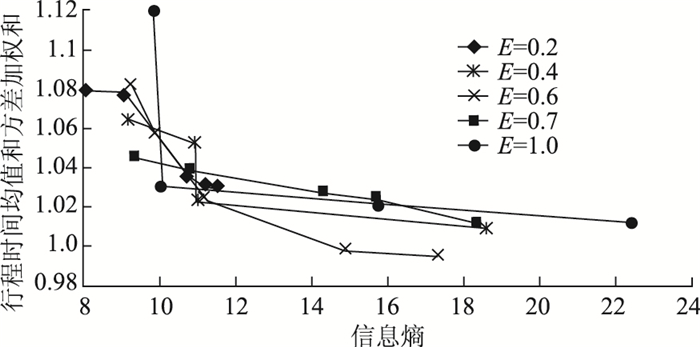
|
| 图 4 E为不同值时的最优解集分布对比 Fig. 4 Comparison of distributions of optimal solution under different E values |
| |
从图 5中清晰可见,当E=1时,个体序号A的ETTT值大于没有部署VMS的路网ETTT值,这说明随着E值越接近1,VMS对路网运行质量的改善作用呈下降趋势,并可能出现比不发布诱导信息还差的局面。对比没有部署VMS的路网,所有选址方案的ETTT值平均下降了2.37%。当E=0.6时,通过部署VMS平均降低了网络总行程时间的3.78%;当E=0.4和E=0.8时,平均降低的网络总行程时间分别为3.22%和3.26%。
|
| 图 5 路网中有无VMS的ETTT值对比 Fig. 5 Comparison of ETTT values between VMS installed and uninstalled in network |
| |
5 结论
本文基于Monte Carlo模拟技术刻画了随机需求和随机供给情景下的路网交通状态,采用出行者信息响应模型描述了路网中出行者的路径选择行为,建立了VMS影响区域信息熵、路网总行程时间均值与标准差加权和最小的双目标VMS选址规划模型。最后采用基于Dial算法的MSA均衡分配和NSGA-Ⅱ算法对模型进行了优化求解,以一个24个节点的简单路网进行了算例分析,验证了本文所提模型及算法的有效性。
需要说明的是,文中采用的各种函数及参数仍需进一步利用实际数据进行标定,以使模型结果更切合实际应用。此外,本文采用的Monte Carlo法虽然具有能够描述复杂多样的系统行为的优点,但其计算量随着网络规模增加而急剧增加。如何设计一套Monte Carlo法结合启发式算法的混合求解算法,在保证解质量的前提下提高求解速度将是下一步研究的重点。
| [1] | 戢晓峰, 覃文文. 考虑局部排队延误的VMS选址双层规划模型[J]. 交通运输系统工程与信息 , 2014, 14 (6) : 194-200 JI Xiao-feng, QING Wen-wen. Bi-level Programming Model for VMS Layout Considering Local Queuing Delay[J]. Journal of Transportation Systems Engineering and Information Technology , 2014, 14 (6) : 194-200 |
| [2] | ZHONG Shi-quan, ZHOU Li-zhen, MA Shou-feng, et al. Effects of Different Factors on Drivers' Guidance Compliance Behaviors under Road Condition Information Shown on VMS[J]. Transportation Research Part A:Policy and Practice , 2012, 46 (9) : 1490-1505 |
| [3] | XU Tian-dong, SUN Li-jun, PENG Zhong-ren. Empirical Analysis and Modeling of Drivers' Response to Variable Message Signs in Shanghai, China[J]. Transportation Research Record , 2011, 2243 : 99-107 |
| [4] | 尚华艳, 黄海军, 高自友. 基于元胞传输模型的可变信息标志选址问题研究[J]. 物理学报 , 2007, 56 (8) : 26-3 SHANG Hua-yan, HUANG Hai-jun, GAO Zi-you. Locating the Variable Message Signs by Cell Transmission Model[J]. Acta Physica Sinica , 2007, 56 (8) : 26-3 |
| [5] | 姜桂艳, 郑祖舵, 白竹, 等. 拥挤条件下可变信息板交通诱导信息对驾驶行为的影响[J]. 吉林大学学报:工学版 , 2006, 36 (2) : 183-187 JIANG Gui-yan, ZHENG Zu-duo, BAI Zhu, et al. Simulation-based Assessment of Variable Message Signs Route Guidance Information under Congestion Condition[J]. Journal of Jilin University:Engineering and Technology Edition , 2006, 36 (2) : 183-187 |
| [6] | CHIU Y C, HUYNH N, MAHMASSANI H S. Determining Optimal Locations for VMS's under Stochastic Incident Scenarios[C]//Transportation Research Board 80th Annual Meeting. Washington, D. C.:TRB, 2001. |
| [7] | CHIU Y C, HUYNH N. Location Configuration Design for Dynamic Message Signs under Stochastic Incident and ATIS Scenarios[J]. Transportation Research Part C:Emerging Technologies , 2007, 15 (1) : 33-50 |
| [8] | LAM W H K, CHAN K S. A Model for Assessing the Effects of Dynamic Travel Time Information via Variable Message Signs[J]. Transportation , 2001, 28 (1) : 79-99 |
| [9] | 袁舒平, 漆凯, 关积珍. 考虑诱导信息影响的可变信息标志优化选址研究:北京南站为例[J]. 交通运输系统工程与信息 , 2011, 11 (S1) : 228-233 YUAN Shu-ping, QI Kai, GUAN Ji-zhen. Research on the Location Choice of the Optimal Variable Messages Signs in Consideration of the Effect of Traffic Guidance Information:Case Study of the Road Area of Beijing South Railway Station[J]. Journal of Transportation Systems Engineering and Information Technology , 2011, 11 (S1) : 228-233 |
| [10] | 杨远舟, 毛宝华, 张笑杰, 等. 基于路径诱导的高负荷路网微循环组织研究[J]. 系统仿真学报 , 2010, 22 (7) : 1580-1584 YAN Yuan-zhou, MAO Bao-hua, ZHANG Xiao-jie, et al. Study on Traffic Micro-circulation Organization in Heavy Traffic Networks Based on Route Guidance[J]. Journal of System Simulation , 2010, 22 (7) : 1580-1584 |
| [11] | FISK C. Some Developments in Equilibrium Traffic Assignment[J]. Transportation Research Part B:Methodological , 1980, 14 (3) : 243-255 |
| [12] | 蒲云, 刘海旭. 基于部分随机用户平衡的可靠性网络设计[J]. 西南交通大学学报 , 2011, 46 (2) : 321-325 PU Yun, LIU Hai-xu. Reliable Network Design Based on Partial Stochastic User Equilibrium[J]. Journal of Southwest Jiaotong University , 2011, 46 (2) : 321-325 |
| [13] | 陈大山, 孙剑, 李克平. 基于SPEA2的城市快速路速度引导多目标优化[J]. 公路交通科技 , 2015, 32 (9) : 128-132 CHEN Da-shan, SUN Jian, LI Ke-ping. Multi-object Optimization of Urban Expressway Speed Guidance Based on SPEA2[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (9) : 128-132 |
| [14] | DEB K, PRATAP A, AGARWAL S, et al. A Fast Elitist Multi-objective Genetic Algorithms:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation , 2002, 6 (2) : 182-197 |
| [15] | 四兵峰, 张好智, 高自由. 求解Logit随机网络配流问题的改进Dial算法[J]. 中国公路学报 , 2009, 22 (1) : 78-83 SI Bing-feng, ZHANG Hao-zhi, GAO Zi-you. Improved Dial's Algorithm for Logit-based Stochastic Traffic Metwork Assignment Problem[J]. China Journal of Highway and Transport , 2009, 22 (1) : 78-83 |
| [16] | LAGUNA M. Applying Robust Optimization to Capacity Expansion of One Location in Telecommunications with Demand Uncertainty[J]. Management Science , 1998, 44 (11) : 101-110 |
 2016, Vol. 33
2016, Vol. 33
