扩展功能
文章信息
- 骆勇鹏, 黄方林, 伍彦斌, 鲁四平, 苏泽平
- LUO Yong-peng, HUANG Fang-lin, WU Yan-bin, LU Si-ping, SU Ze-ping
- 基于逐步回归分析和Bootstrap重抽样的铁路钢桁桥不确定参数识别
- Identification of Uncertain Parameters of Railway Steel Truss Bridge Based on Stepwise Regression and Bootstrap Resampling
- 公路交通科技, 2016, 33(11): 104-110
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 104-110
- 10.3969/j.issn.1002-0268.2016.11.016
-
文章历史
- 收稿日期: 2016-03-30
目前结构设计分析往往都是在模型、参数等因素已经确定的情况下,采用确定性的方法进行仿真分析。由于结构尺寸误差、材料特性等存在一定的不确定性,这些不确定性又使结构响应具有变异性,导致研究人员难以准确地对结构的实际特性进行分析与判断[1]。因此,如何准确量化这些不确定性成为当前工程界迫切需要解决的问题之一[2]。目前,不确定性分析方法中应用较为广泛的是基于概率的分析方法,如随机模型修正[3]和蒙特卡罗法[4]等。随机模型修正对应于多组测试值,认为结构响应是分布范围,修正参数结果为分布参数或者概率密度函数[5]。该方法通常假设不确定性参数为服从某种概率分布的随机变量,通过构建一个反问题来求得结构参数的概率统计特征[6]。其在每个迭代优化过程都需要进行不确定性的正反向分析,因此需要较高的计算成本。同时,由于考虑了不确定性,优化过程容易出现病态的优化问题,导致无法收敛的情况。为了简化随机模型修正过程,文献[7]提出将随机模型修正分解为一系列确定性修正过程,通过大量确定性样本来反演得到大量参数,从而进行概率统计分析。该方法概念简单,使得复杂工程结构的随机模型修正问题更容易实现。
然而,在实际工程结构中,由于现场测试条件及测试成本等因素的限制,往往仅能获得少量的样本数据,不足以形成有效的分布,无法为不确定性参数识别提供有效的概率信息。若是人为假定不确定性参数服从某种概率分布,当此假设与现实不符时,可能导致错误的计算结果。为了解决该问题,笔者结合响应面模型修正和Bootstrap重抽样技术,提出一种改进的不确定性参数识别方法。该方法首先采用逐步回归分析(Stepwise Regression,SR)建立表达参数与响应之间的复杂关系的响应面模型。然后采用Bootstrap抽样技术对有限的实测数据进行重新抽样,得到大量符合原始数据特征的Bootstrap样本。以Bootstrap样本为输入,结合响应面模型构造优化反演过程来计算各个Bootstrap样本所对应的一组参数,进而基于大量样本数据统计得到不确定性参数的均值和标准差。采用以一组试验钢板和一座铁路钢桁桥来验证所提方法的可行性与可靠性。
1 基于SR的响应面模型修正方法响应面模型修正是通过对样本数据进行回归分析,以显式多项式逼近目标函数与设计变量之间的复杂隐式函数关系,得到简化的结构模型,代替初始有限元模型,然后在此基础上进行迭代修正[8-9]。常用二次多项式响应面如式(1)所示。
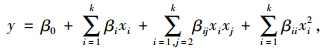
|
(1) |
式中, β0,βi,βii,βij是待定系数;xi为参数主效应;xixj为参数之间的相互效应。
随着变量数和多项式展开阶次的增加,响应面模型中的待定系数急剧增加。然而,并不是所有展开项都对响应量具有显著影响,因此有必要将次要项剔除,从而在保证计算精度的前提下有效地减少待定系数,提高计算效率。为此,笔者引入逐步回归分析方法进行响应面拟合。该方法引入或者剔除一个变量都称为逐步回归的一步,每一步都要进行F检验,以保证在引人新变量前回归方程中只含有对y影响显著的变量,而不显著的变量已被剔除。
假设回归方程中引入了L项,则其中的第i项的显著性可由下式衡量:
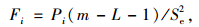
|
(2) |
式中,Pi为偏回归平方和;Se2为残差平方和;L为已引入的展开项数;m为样本数。
首先确定显著水平α,然后确定引入多项式的临界值FL1和剔除临界值FL2。在考虑全部自变量对y的显著程度大小,若其Fi值大于引入临界值FL1,则说明此变量是显著的,需引入回归方程。己被引入回归方程的变量在引入新变量后也可能造成显著性下降,从而需要从回归方程中剔除出去。因此引入后需要重新计算各展开项的Pi,并确定具有最小偏回归平方和的展开项的F检验值,若该值大于FL2,则说明该展开项是显著的,需要保留在回归方程中;反之,则剔除[10-12]。
在得到响应面模型后,需要对其精度检验。目前常用的3种准则的表达式如下:
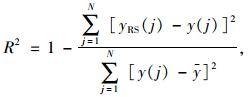
|
(3) |
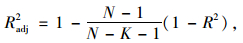
|
(4) |
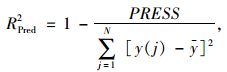
|
(5) |
式中,yRS为响应面模型计算结果;y为有限元计算结果;N为设计空间上检验点的数量;y为有限元计算结果的平均值;K为回归方程的项数;PRESS为预测残差平方和,是对模型拟合设计空间样本程度的衡量。当3种精度检验值都接近于1且差异较小时,可以认为所建立的响应面模型可以很好地拟合样本且具有较好的预测能力。
最后,以得到响应面模型代替有限元模型进行修正,因此有限元模型修正可转化为以下的优化问题:
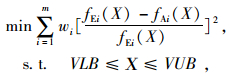
|
(6) |
式中, X为设计参数;fE为试验值;fA为分析值;wi为权重系数;VLB和VUB是参数设计空间范围。
2 不确定性参数识别流程在实际工程结构中,由于现场测试条件及测试成本等因素的限制,往往仅能获得少量的样本数据,不足以形成有效的分布,无法为不确定性参数识别提高准确的概率信息。美国斯坦福大学Efron教授于1979年提出的Bootstrap法可有效解决该问题。Bootstrap法是一种基于试验观测数据的模拟再抽样来分析不确定性的工具,它运用模拟再抽样技术代替理论分析,采用试验观测数据的统计特征代替真实母体的特征。在摆脱了传统统计方法中对于分布假定依赖的条件下,基于有限的试验观测数据模拟再抽样出大量符合原数据特征的模拟样本,从而为不确定性分析提供了足够的样本,然后在此基础上进行统计推断[13-14]。为此,笔者结合响应面模型修正和Bootstrap重抽样技术,提出一种新的不确定性参数识别方法。所提方法的计算流程如下:
(1) 假设结构的实测响应X=(X1, X2, …, Xn)是来自总体F、容量为n的样本, x=(x1, x2, …, xn)是一个已知的原生样本。根据该样本即可构造原生样本的经验分布函数,如式(7)所示。
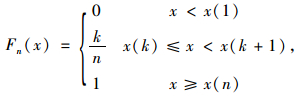
|
(7) |
式中,k为x(1), x(2),…, x(n)中不大于x(k)的样本个数,1≤k < n-1, 其中x(1)≤x(2)≤…≤x(n)是x1, x2, …, xn由小到大排序后的统计量。
(2) 相继地、独立地从Fn中抽取容量为n的Bootstrap样本x1*, x2*, …, xn*。
(3) 为快速地进行响应计算和参数反演,先通过试验设计和逐步回归分析方法建立表达设计参数与响应之间复杂关系的前i阶模态频率的响应面模型yi。并根据式(6)构造优化目标函数。
(4) 将步骤(2)抽样得到的bootstrap样本分别代入优化目标函数,采用序列二次规划算法反演得到第j个设计参数值的n个值Pj1*, Pj2*, …, Pjn*。构造统计量。
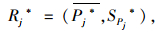
|
(8) |
式中,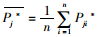
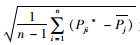
(5) 独立重复步骤(2)至步骤(4) B次,得到B个Rj*统计量值,最后根据式(9)和式(10)即可计算第j个参数的均值和标准差。
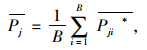
|
(9) |
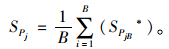
|
(10) |
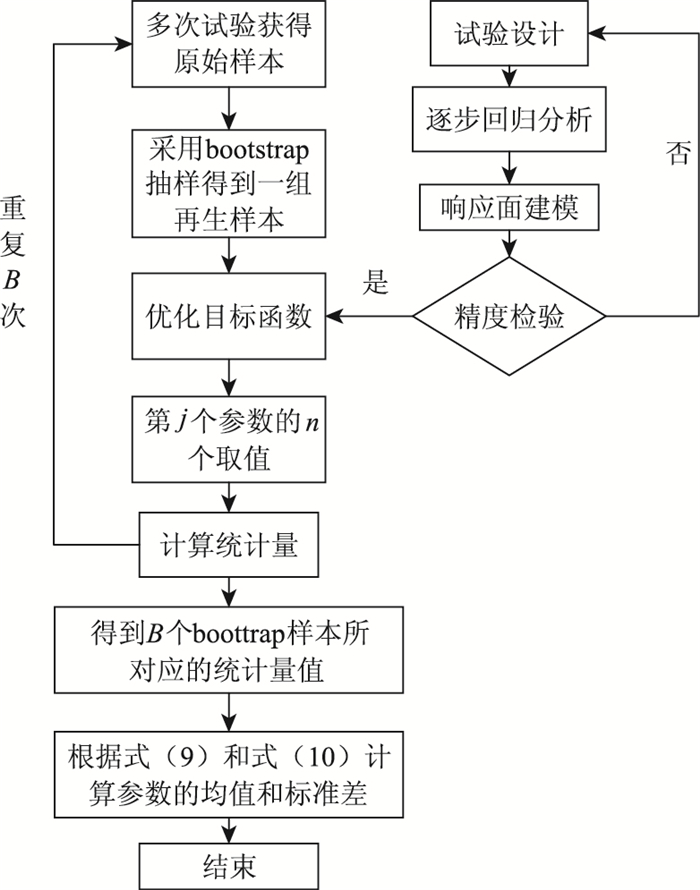
综上所述所提方法的计算流程如图 1所示。
|
| 图 1 所提方法的计算流程图 Fig. 1 Flowchart of calculation by proposed method |
| |
3 钢板试验验证
以33块具有相同名义尺寸及材料参数的钢板为研究对象。钢板的名义尺寸为564 mm× 110 mm × 1.45 mm,弹性模量、剪切模量、质量密度的名义取值分别为210, 83 GPa及7 860 kg/m3。采用Shell单元建立钢板的初始有限元模型,有限元模型的物理参数取名义尺寸及材料参数的名义取值。
为了预测参数的不确定性,在自由-自由边界条件下,采用锤击法对这33块钢板进行模态试验,得到33块钢板的前5阶模态频率值及其统计特征值,如表 1所示[15]。假设模态频率的变异性是由材料参数不确定性所引起的,采用所提方法识别钢板的不确定性参数。
| f1 | f2 | f3 | f4 | f5 | |
| 区间 | [23.94, 24.4] | [66.5, 67.53] | [76.24, 78.91] | [131.31, 133.03] | [156.31, 160.94] |
| 均值 | 24.12 | 66.92 | 77.65 | 131.97 | 158.8 |
| 标准差 | 0.11 | 0.25 | 0.57 | 0.42 | 0.97 |
以钢板的材料参数E和G作为修正参数,研究表明,待修正参数的初始区间范围(不确定性大小)对参数区间的最终估计精度影响很小,可设置较大[7]。考虑到钢材材料参数通常具有5%的变异性,结合相关文献钢板单轴拉伸试验结果,确定参数E,G的初始区间分别为[199.5,220.5]、[78.85,87.15]。采用中心复合设计确定试验点并计算试验点所对应的响应,如表 2所示。为提高修正效率,采用逐步回归分析方法拟合前5阶模态频率的响应面模型,式(11)为第1阶模态频率的响应面模型表达式。
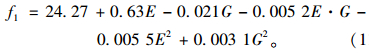
|
(11) |
| 序号 | E | G | f1/Hz | f2/Hz | f3/Hz | f4/Hz | f5/Hz |
| 1 | 0.85 | 0.85 | 24.87 | 69.14 | 78.41 | 137.06 | 160.83 |
| 2 | 0.50 | 0.50 | 24.27 | 67.49 | 76.34 | 133.80 | 156.61 |
| 3 | 0.50 | 0.50 | 24.27 | 67.49 | 76.34 | 133.80 | 156.61 |
| 4 | 0.50 | 0.00 | 24.31 | 67.81 | 73.42 | 134.92 | 151.11 |
 |  |  |  |  |  | 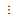 | 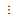 |
| 12 | 1.00 | 0.50 | 25.15 | 70.11 | 76.41 | 139.43 | 157.19 |
| 13 | 0.15 | 0.15 | 23.66 | 65.79 | 74.23 | 130.46 | 152.31 |
由于样本数量较小,难以准确估计实测频率的统计特征值,为此以实测得到的33组模态频率值作为原始样本,采用Bootstrap重抽样技术,每次生成1组前5阶模态频率,每阶模态频率有33个取值,结合响应面模型,构建确定性的优化反问题,计算得到33组材料参数取值,经统计分析可计算每组材料参数的均值和标准差。重复抽样1 000次可计算得到1 000组材料参数的均值和标准差。根据式(9)和式(10)估计得到E和G的均值和标准差,如表 3所示。为了方便比较分析,表 3中还列出了随机模型修正法[15]及改进的随机模型修正法[7]的识别结果。从表 3可知所提方法预测的弹性模量和剪切模量值与分别采用随机模型修正法[15]及改进的随机模型修正法[7]得到的预测值的误差很小,符合钢材材料特性取值。频率预测均值结果如表 4所示。由表 4可知所提方法的频率预测均值误差比随机模型修正法[15]及改进的随机模型修正法[7]的误差来得小。从表 5的频率标准差比较结果可知,3种方法修正后的预测频率标准差均有所改善,但误差仍然较大,因此如何提高标准差的修正精度仍是一个亟待解决的问题。根据图 2和图 3可知,所提方法预测频率分布范围与实测分布范围较为接近,验证了所识别的不确定性参数取值的准确性。
| 预测值 | 随机模型修正 | 改进的随机模型修正 | 所提方法 | |||||
| E | G | E | G | E | G | |||
| 均值 | 209.6 | 83.8 | 209.2 | 84.9 | 206.7 | 85.4 | ||
| 标准差 | 1.6 | 1.22 | 2.14 | 1.09 | 1.02 | 0.95 | ||
| 模态 | 实测值 | 随机模型修正法 | 改进的随机模型修正法 | 所提方法 | |||||
| 修正后/Hz | 误差/% | 修正后/Hz | 误差/% | 修正后/Hz | 误差/% | ||||
| 1 | 24.12 | 24.23 | 0.47 | 24.21 | 0.37 | 24.09 | -0.12 | ||
| 2 | 66.92 | 67.04 | 0.18 | 66.93 | 0.01 | 66.87 | -0.07 | ||
| 3 | 77.65 | 76.67 | 1.25 | 77.41 | 0.31 | 77.65 | 0 | ||
| 4 | 131.97 | 131.93 | 0.03 | 131.62 | 0.27 | 132.38 | 0.31 | ||
| 5 | 158.8 | 156.86 | 1.22 | 158.31 | 0.31 | 159.01 | -0.13 | ||
| 模态 | 实测值 | 随机模型修正法 | 改进的随机模型修正法 | 所提方法 | |||||
| 修正后/ Hz | 误差/ % | 修正后/ Hz | 误差/ % | 修正后/ Hz | 误差/ % | ||||
| 1 | 0.11 | 0.10 | -9.09 | 0.12 | 10.91 | 0.08 | -27.27 | ||
| 2 | 0.25 | 0.24 | -4.00 | 0.34 | 36.00 | 0.18 | -28.00 | ||
| 3 | 0.57 | 0.53 | -7.02 | 0.49 | -14.04 | 0.42 | -26.31 | ||
| 4 | 0.42 | 0.47 | 11.90 | 0.66 | 57.14 | 0.29 | -30.79 | ||
| 5 | 0.97 | 1.04 | 7.22 | 0.98 | 0.82 | 0.74 | -23.33 | ||
|
| 图 2 预测和实测的钢板前3阶模态频率散点图(单位:Hz) Fig. 2 Scattergram of predicted and measured first 3 orders mode frequencies (unit:Hz) |
| |
|
| 图 3 预测和实测的第3,4,5阶模态频率散点图(单位:Hz) Fig. 3 Scattergram of predicted and measured 3rd, 4th, 5 order mode frequencies (unit:Hz) |
| |
4 既有铁路钢桁架桥不确定性参数识别
南京长江大桥是我国首座自行设计和建造的公铁两用桥梁。上部结构由10孔钢梁组成,浦口岸第1孔为128 m的简支钢桁梁,其余9孔为3联3等跨160 m的连续钢桁梁。为了验证所提方法在复杂土木工程结构不确定性参数识别上应用的可行性及可靠性,以南京长江大桥中间联为研究对象,根据实测频率值反演结构参数的统计特征值。文献[16]详细介绍了该桥的振动测试,本文不再赘述。
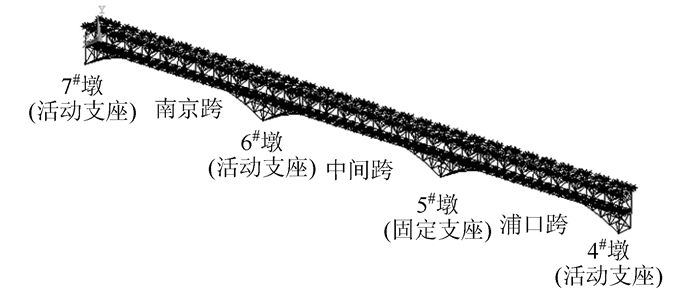
南京长江大桥中间联的有限元模型采用几种不同单元类型来模拟不同的结构构件,采用三维梁单元beam4模拟主桁杆件、铁路纵梁等,采用质量单元mass21加在模型的上、下平联相关节点上来考虑铁路轨枕和无缝钢轨等构件对结构的影响。模型中的Beam44梁单元4 395个,Mass21质量单元552个,梁截面类型51种,节点总数1 597个。有限元模型如图 4所示。
|
| 图 4 有限元模型图 Fig. 4 Finite element model |
| |
研究表明,钢材的弹性模量受环境因素(尤其是温度因素)的影响会产生一定程度的变化[6]。同时,铁路轨枕和无缝钢轨等构件对结构的影响采用等效质量来考虑,具有较大的不确定性。因此本次识别以主桁杆件的弹性模量E、公路桥面及公路纵梁质量M1、钢轨及轻轨等效质量M2这3个参数作为不确定性参数。初始材料参数取值如表 6所示。
| 结构参数 | 初始值 | 上下限 |
| E/GPa | 210 | 190~230 |
| M1/kg | 11 256.8 | 7 880~14 633 |
| M2/kg | 540.5 | 378~702 |
为模拟不同时段的模态频率值,笔者假设3个参数的实际均值为E=203.6 GPa, M1=8 503.9 kg, M2=534.8 kg,这3个参数分别具有3%,10%,10%的不确定性,采用拉丁超立方抽样抽取30个样本并计算样本所对应的模态频率值作为模拟实测模态频率值。30组前5阶模态频率的概率统计特征值如表 7所示。
| 频率 | 修正值 | 实测值 | 相对误差 | |||||
| 均值 | 标准差 | 均值 | 标准差 | 均值 | 标准差 | |||
| V1 | 0.603 5 | 0.008 7 | 0.604 4 | 0.013 2 | -0.16 | -34.55 | ||
| V2 | 1.392 5 | 0.016 2 | 1.392 6 | 0.026 4 | 0.00 | -38.40 | ||
| V3 | 2.127 5 | 0.013 7 | 2.123 3 | 0.024 4 | 0.20 | -43.75 | ||
| H1 | 1.068 3 | 0.005 4 | 1.072 7 | 0.009 0 | -0.41 | -39.29 | ||
| H2 | 1.145 4 | 0.005 9 | 1.141 9 | 0.006 8 | 0.30 | -12.65 | ||
采用中心复合设计进行试验设计,然后在样本点上进行有限元分析得到样本数据,最后计算各展开项的贡献值,确定引入和剔除的界限值,在逐步回归分析过程中剔除对响应影响不显著的展开项,得到前5阶模态频率响应面模型。限于篇幅,本文给出竖向第1阶频率响应面模型表达式如式(12)所示。
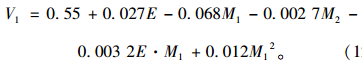
|
(12) |
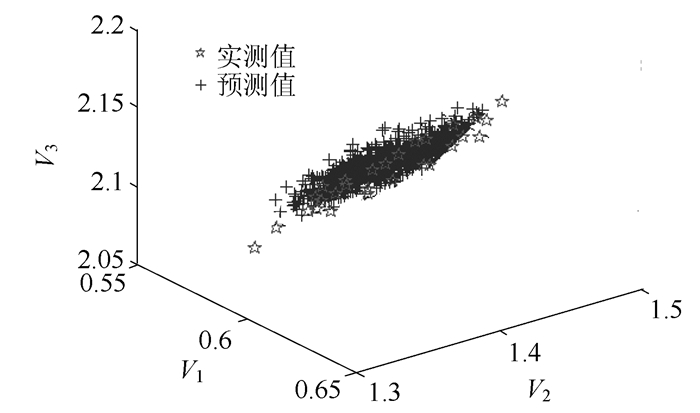
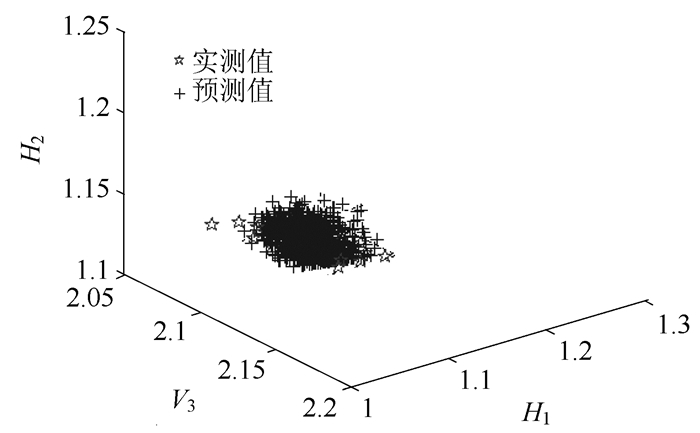
按照所提方法识别得到3个材料参数均值的标准差,如表 8所示。从表 8可以看出,预测与实测的材料参数统计特征值(均值和标准差)非常接近,误差较小,这说明所提方法可以准确地识别不确定性参数的统计特征值。表 7为预测和实测的频率统计特征值(均值和标准差)的比较结果,从结果比较可得,预测频率的均值与实测频率的均值基本一致,最大误差仅为-0.41%。从图 5和图 6可以看出,预测频率分布与实测频率分布吻合程度良好,这说明所提方法具有较高的识别精度。
| 参数 | 初始值 | 实测值 | 预测值 | |||||
| 均值 | 标准差 | 均值 | 标准差 | 均值 | 标准差 | |||
| E/GPa | 210.00 | 16.53 | 203.6 | 2.39 | 203.32 | 2.37 | ||
| M1/kg | 11 256.8 | 2 790.15 | 8 503.9 | 493.78 | 8 510.03 | 407.27 | ||
| M2/kg | 540.5 | 133.87 | 534.8 | 31.53 | 535.51 | 11.52 | ||
|
| 图 5 实测和预测的前3阶竖向模态频率散点图(单位:Hz) Fig. 5 Scattergram of predicted and measured first 3 orders vertical mode frequencies (unit:Hz) |
| |
|
| 图 6 预测和实测的竖向第3阶及横向前2阶模态频率散点图(单位:Hz) Fig. 6 Scattergram of predicted and measured 3 order vertical and first 2 orders horizontal mode frequencies (unit:Hz) |
| |
5 结论
提出一种基于逐步回归分析和Bootstrap重抽样的不确定性参数识别方法。以一组钢板试验和铁路钢桁架桥算例来验证所提方法的可行性及可靠性,得到以下几点结论。
(1) 所提方法将不确定性量化过程分解为一系列确定性的模型修正过程,简化了不确定性正反分析过程且可准确地识别不确定性参数的概率统计特征值。
(2) 采用逐步回归分析方法进行响应面拟合可在保证计算精度的前提下有效地减少待定系数。用响应面模型代替有限元模型进行计算,通过确定性优化反演可快速识别不确定性参数取值,提高了计算效率。
(3) 引入Bootstrap重抽样技术,通过对实测的多组频率进行重抽样得到符合原始数据特征的Bootstrap样本,解决了小样本数据下无法准确获得响应的统计特征值和概率分布问题。
| [1] | 侯立群, 赵雪峰, 欧进萍, 等. 结构损伤诊断不确定性方法研究进展[J]. 振动与冲击 , 2014, 33 (18) : 50-58 HOU Li-qun, ZHAO Xue-feng, OU Jin-ping, et al. A Review of Nondeterministic Methods for Structural Damage Diagnosis[J]. Journal of Vibration and Shock , 2014, 33 (18) : 50-58 |
| [2] | BECK J L, KATAFYGIOTIS L S. Updating Models and Their Uncertainties. I:Bayesian Statistical Framework[J]. Journal of Engineering Mechanics , 1998, 124 (4) : 455-461 |
| [3] | STEENACKERS G, GUILLAUME P. Finite Element Model Updating Taking into Account the Uncertainty on the Modal Parameters Estimates[J]. Journal of Sound and Vibration , 2006, 296 (4) : 919-934 |
| [4] | MARES C, MOTTERSHEAD J E, FRISWELL M I. Stochastic Model Updating:Part1-Theory and Simulated Example[J]. Mechanical Systems and Signal Processing , 2006, 20 (7) : 1674-1695 |
| [5] | 万华平.结构动力不确定性及其随机模型修正方法研究[D].长沙:中南大学, 2014. WAN Hua-ping. Study on Uncertainty in Structural Dynamics and Stochastic Model Updating[D]. Changsha:Central South University, 2014. |
| [6] | 姜东, 费庆国, 吴邵庆. 基于区间分析的不确定性结构动力学模型修正方法[J]. 振动工程学报 , 2015, 28 (3) : 352-358 JIANG Dong, FEI Qing-guo, WU Shao-qing. Updating of Structural Dynamics Model with Uncertainty Based on Interval Analysis[J]. Journal of Vibration Engineering , 2015, 28 (3) : 352-358 |
| [7] | 方圣恩, 林友勤, 夏樟华. 考虑结构参数不确定性的随机模型修正方法[J]. 振动、测试与诊断 , 2014, 34 (5) : 832-837 FANG Sheng-en, LIN You-qin, XIA Zhang-hua. Stochastic Model Updating Considering Uncertainties of Structural Parameters[J]. Journal of Vibration, Measurement & Diagnosis , 2014, 34 (5) : 832-837 |
| [8] | REN W X, FANG S E, DENG M Y. Response Surface-Based Finite Element Model Updating Using Structural Static Response[J]. Journal of Engineering Mechanics , 2011, 137 (4) : 248-257 |
| [9] | 韩建平, 骆勇鹏. 基于响应面的刚构-连续组合梁桥有限元模型静动力修正[J]. 公路交通科技 , 2013, 30 (11) : 53-61 HAN Jian-ping, LUO Yong-peng. Response Surface Based Finite Element Model Updating for a Rigid Frame Continuous Composite Girder Bridge Using Static and Dynamic Test Data[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (11) : 53-61 |
| [10] | 骆勇鹏, 黄方林, 廖明皓, 等. 基于逐步回归分析的既有铁路钢桁架桥有限元模型修正[J]. 铁道科学与工程学报 , 2015, 12 (5) : 1111-1115 LUO Yong-peng, HUANG Fang-lin, LIAO Ming-hao, et al. Existing Railway Steel Truss Bridge Finite Element Model Updating Based on Stepwise Regression[J]. Journal of Railway Science and Engineering , 2015, 12 (5) : 1111-1115 |
| [11] | 杨绿峰, 杨显峰, 余波, 等. 基于逐步回归分析的随机响应面法[J]. 计算力学学报 , 2013, 30 (1) : 88-93 YANG Lü-feng, YANG Xian-feng, YU Bo, et al. Improved Stochastic Response Surface Method Based on Stepwise Regression Analysis[J]. Chinese Journal of Computational Mechanics , 2013, 30 (1) : 88-93 |
| [12] | 周纪芗. 实用回归分析方法[M]. 上海: 上海科学技术出版社, 1990 . ZHOU Ji-xiang. Practical Methods for Regression Analysis[M]. Shanghai: Shanghai Science & Technology Press, 1990 . |
| [13] | EFRON B, TIBSHIRANI R. An Introduction to Bootstrap[M]. New York: Chapman & Hall Ltd., 1993 . |
| [14] | HALL P. Theoretical Comparison of Bootstrap Confidence Intervals[J]. Annals of Statistics , 1988, 16 (3) : 927-953 |
| [15] | HUSAIN N A, KHODAPARAST H H, OUYANG H J. Parameter Selections for Stochastic Uncertainty in Dynamic Models of Simple and Complicated Structures[C]//Proceedings of the 10th International Conference on Recent Advances in Structural Dynamics. Southampton:University of Southampton, 2010. |
| [16] | 何旭辉, 余志武, 陈政清. 既有铁路钢桁梁桥基准有限元模型建立与验证[J]. 振动与冲击 , 2007, 26 (12) : 117-121 HE Xu-hui, YU Zhi-wu, CHEN Zheng-qing. Establishment and Verification of the Baseline 3D Finite-element Model of Existing Railway Steel Truss Bridge[J]. Journal of Vibration and Shock , 2007, 26 (12) : 117-121 |
 2016, Vol. 33
2016, Vol. 33
