扩展功能
文章信息
- 魏家乐
- WEI Jia-le
- 自锚式悬索桥空缆线形计算方法研究
- Study on Calculation Method of Free Cable Shape for Self-anchored Suspension Bridge
- 公路交通科技, 2016, 33(11): 93-98
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 93-98
- 10.3969/j.issn.1002-0268.2016.11.014
-
文章历史
- 收稿日期: 2016-02-24
主缆空缆线形的准确计算和精确控制是悬索桥施工的关键,一旦主缆施工架设完毕,最终的主缆线形及内力能否达到设计要求即基本确定。在后期施工过程中主缆线形及内力完全取决于结构体系中的结构自重、施工荷载作用(包含温度),后期的索力和标高基本没有调整余地。因此,悬索桥主缆在安装完毕自重作用下的空缆线形的计算分析和精确控制就成为保证悬索桥施工过程成功控制的关键[1-3]。
对于自锚式悬索桥,一般采取先梁后缆的施工顺序,空缆状态线形分析控制是一个极其复杂的问题,包括主缆无应力长度的准确计算和下料、主缆初始垂度的计算和控制、塔顶主索鞍的初始预偏量计算、索夹预偏量的计算、加劲梁安装时纵向压缩补偿量的计算和安装控制等等。主缆各索段无应力索长和索夹预偏量的计算由成桥合理状态的有应力索长和索夹位置反算而得。索鞍预偏是为了保证桥塔受力安全而通过调整空缆状态索塔两侧主缆水平分力大小而采取的措施。主缆在加劲梁锚固位置需计算加劲梁压缩量而进行预先补偿得到。这些量计算确定后,自锚式悬索桥的空缆线形也随即确定。
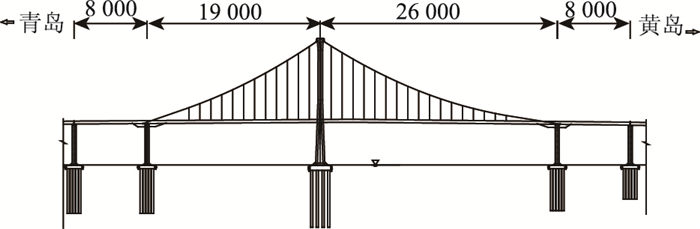
1 工程背景及有限元模型的建立大沽河航道桥是青岛海湾大桥三座通航孔桥之一,是其跨径最大的控制性工程,结构形式为独塔空间索面自锚式悬索桥,跨径布置为(80+190+260+80)=610 m。主跨及边跨为悬吊结构,主缆主跨矢跨比为1/12.53,边跨矢跨比为1/18.04。主缆为两根空间缆,横桥向中心间距在塔顶为2.5 m,在主跨侧后锚面为6.5 m,在边跨侧后锚面为7.8 m。桥型布置图如图 1所示。
|
| 图 1 桥型布置示意(单位:cm) Fig. 1 Layout of bridge (unit:cm) |
| |
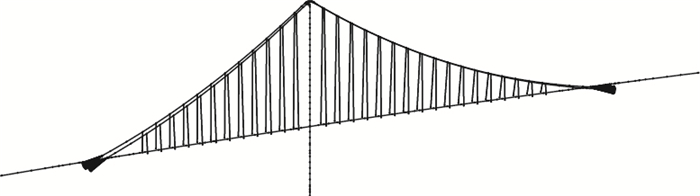
采用空间有限元程序MIDAS/Civil建立有限元模型进行结构分析,模型共有单元540个,节点602个,结构离散图如图 2所示,模型包含索塔、加劲梁、主缆和吊索等构件,其中索塔及加劲梁采用梁单元进行模拟,主缆和吊索采用只受拉索单元模拟。对于边界条件:索塔塔底直接与大地固结,辅助墩和过渡墩墩顶处对加劲梁采用与实际支座约束方向一致的一般支撑模拟;主缆散索各锚固点与加劲梁之间采用刚性连接,主缆与塔顶之间在不同施工阶段根据实际情况采用多种弹簧进行连接,主缆和吊索之间共用节点,吊索与加劲梁之间采用刚性连接。以下对空缆线形、主缆无应力长度、塔顶主索鞍的预偏量、索夹预偏量、散索鞍预偏量及主缆在加劲梁上锚点坐标等的有限元分析展开论述。
|
| 图 2 桥梁有限元模型 Fig. 2 FE model of bridge |
| |
2 空缆线形的有限元计算方法 2.1 非线性有限元法
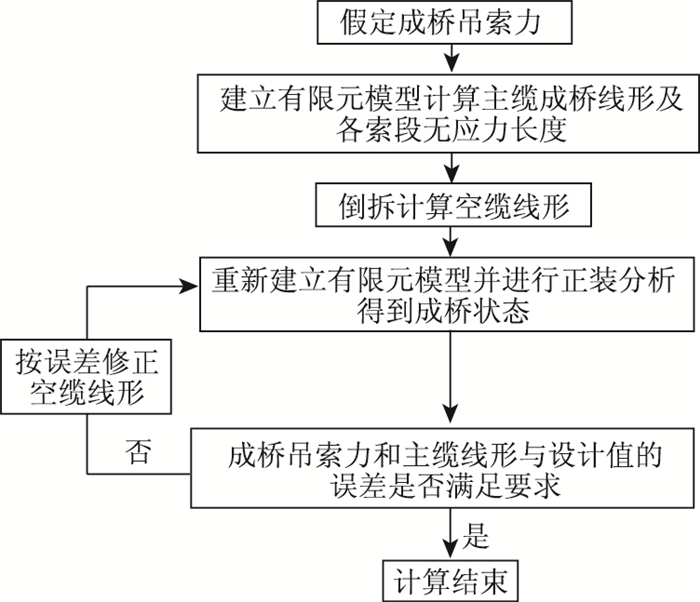
按照综合倒装-正装-无应力状态法的施工控制方法进行计算。通过建立非线性有限元模型,已知成桥吊索力,计算主缆成桥线形及各索段无应力长度,倒拆得到近似的空缆线形(包含索鞍、索夹的预偏量等),通过模拟施工过程正装计算得到成桥状态的结构几何形状参数,将其与设计成桥状态几何形状参数进行比较,若误差不满足精度要求,则修改空缆线形及索鞍、索夹的坐标,重复上述计算过程,直到满足精度要求为止[4]。最终就可以得到包含主缆无应力长度、索鞍及索夹预偏量等的精确空缆线形。有限元计算流程如图 3所示。
|
| 图 3 有限元计算流程图 Fig. 3 Flowchart of FE calculation |
| |
青岛海湾大桥大沽河航道桥主缆空缆线形计算结果如表 1所示。此空缆线形包含了塔顶索鞍预偏、索夹预偏、散索套预偏、加劲梁锚点预偏等信息。
| 索夹编号 | 纵坐标 | 横坐标 | 竖坐标 |
| 后锚面中心 | K26+465.466 | -3.900 | 54.011 |
| 散索套 | 480.828 | -3.753 | 59.832 |
| B1 | 515.677 | -3.266 | 73.787 |
| B2 | 527.524 | -3.100 | 79.081 |
| B3 | 539.392 | -2.934 | 84.671 |
| B4 | 551.291 | -2.767 | 90.561 |
| B5 | 563.225 | -2.600 | 96.758 |
| B6 | 575.173 | -2.433 | 103.267 |
| B7 | 587.156 | -2.265 | 110.094 |
| B8 | 599.174 | -2.097 | 117.244 |
| B9 | 611.213 | -1.928 | 124.723 |
| B10 | 623.274 | -1.759 | 132.537 |
| B11 | 635.379 | -1.590 | 140.692 |
| B12 | 647.519 | -1.420 | 149.193 |
| 索鞍中心 | 659.620 | -1.288 | 156.720 |
| Z1 | 671.924 | -1.351 | 149.998 |
| Z2 | 684.223 | -1.452 | 142.304 |
| Z3 | 696.48 | -1.553 | 134.957 |
| Z4 | 708.694 | -1.653 | 127.950 |
| Z5 | 720.872 | -1.754 | 121.278 |
| Z6 | 733.015 | -1.853 | 114.935 |
| Z7 | 745.108 | -1.953 | 108.913 |
| Z8 | 757.196 | -2.052 | 103.208 |
| Z9 | 769.228 | -2.151 | 97.812 |
| Z10 | 781.229 | -2.249 | 92.719 |
| Z11 | 793.196 | -2.348 | 87.925 |
| Z12 | 805.116 | -2.446 | 83.424 |
| Z13 | 817.035 | -2.544 | 79.210 |
| Z14 | 828.926 | -2.641 | 75.278 |
| Z15 | 840.789 | -2.739 | 71.624 |
| Z16 | 852.641 | -2.836 | 68.243 |
| Z17 | 864.471 | -2.933 | 65.129 |
| 散索套 | 907.094 | -3.284 | 56.110 |
| 后锚面中心 | 923.269 | -3.250 | 53.350 |
2.2 关键细节的有限元模拟方法
在自锚式悬索桥计算时,主缆在塔顶主索鞍处一般采用IP点进行模拟计算,在散索鞍至锚固点一般也以中心索股代替实际散索情况进行计算,如此简单模拟计算对于桥梁设计以及成桥阶段计算来讲基本可行。但在实际不同的施工阶段,主缆在主索鞍上的切点是不断变化的,散索鞍至锚固点索股的
合力并不一定作用于中心索股,因此对于实际桥梁施工控制来讲则会产生不可忽略的较大误差,导致主缆在主索鞍及散索鞍附近坐标偏差较大。因此,为了准确计算自锚式悬索桥空缆线形,从而对桥梁进行精确控制,必须精确模拟主索鞍与主缆切点及散索鞍至锚固点的散索问题。在该桥实际控制中,提出了如下有限元模拟方法,该方法在实桥控制中取得了良好的效果,实测空缆状态各点坐标与计算值吻合非常好。
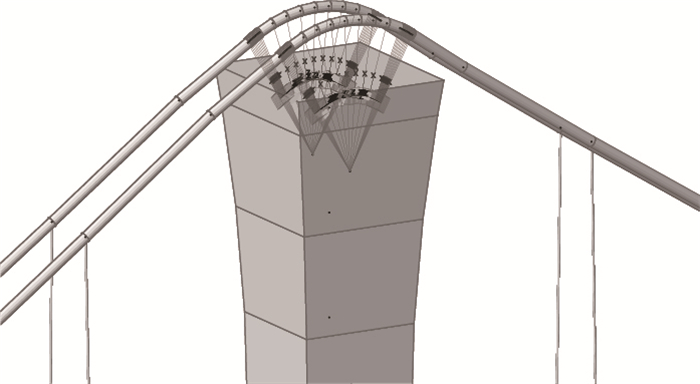
(1) 精确模拟主索鞍与主缆切点,如图 4所示:在主索鞍圆心建立节点与塔顶节点相连(不同施工阶段连接方式不同),将索鞍处主缆分成多段单元,索鞍顶点处单元长度可较长,主缆与索鞍切点附近则精细划分(单元长度5~10 mm可满足工程精度要求),该区段范围进行估算保证切点变化不超出该范围,再从索鞍圆心节点建立只受压弹簧与主缆各节点相连。在不同施工阶段下,主缆切点将发生变化(例如空缆状态切点比成桥状态偏高)。当主缆切点向上变化时,切点以下弹簧出现拉力,则自动失效,依然存在压力的最下方弹簧节点即为切点;当主缆切点向下变化时,初始切点以下弹簧出现压力,最下方弹簧节点即为切点。
|
| 图 4 主索鞍与主缆切点变化模拟 Fig. 4 Simulation of tangent point of saddle and cable |
| |
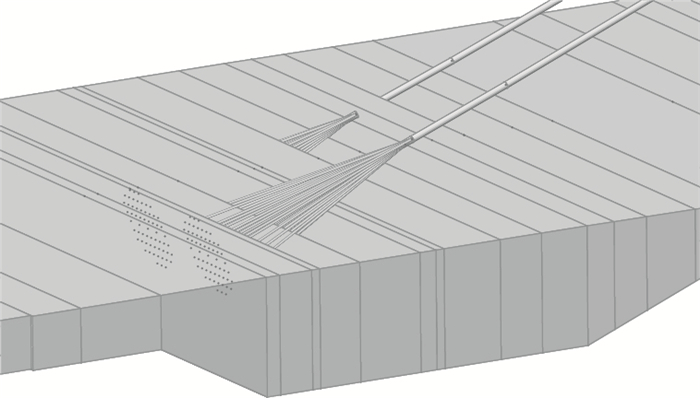
(2) 精确模拟主缆散索,如图 5所示:主缆在散索鞍处分散成若干索股后锚固于加劲梁上,各索股空间锚固角度均不相同,按照实际散开的索股参数模拟即可。在设计成桥状态,各散索索股合力作用于中心索股;而在空缆状态及其他施工阶段,由于缆形缆力的变化,各散索索股分力重新平衡反过来影响了主缆在散索点附近坐标的变化。
|
| 图 5 主缆散索模拟 Fig. 5 Simulation of main splayed cable |
| |
3 主缆无应力长度的计算与修正方法
为了使成桥状态的结构线形和内力均达到设计要求,保证施工质量,主缆无应力长度的计算准确性在整个施工控制中具有决定性的作用[5-7]。
3.1 主缆无应力长度的计算方法主缆无应力长度是指索股在设计温度下,截面应力为零时的长度。主缆有应力长度则是主缆受力后的表现长度。不难看出,有应力长度跟主缆所受荷载大小有关,在不同的荷载量作用下的有应力长度是不同的;而无应力长度是一个常量,无论荷载如何变化,其值均保持恒定不变。自锚式悬索桥在施工控制过程中,主缆的无应力长度是通过成桥状态下有应力长度扣除各项荷载变形得到的,该值是索股加工长度的依据。
(1) 主缆有应力索长计算
由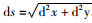
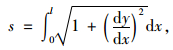
|
而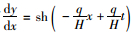
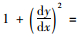
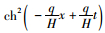
这样就可以解得索段有应力索长为:
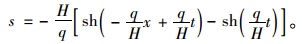
|
(1) |
(2) 主缆的弹性伸长量计算
在悬索中任取一微分单元ds,有: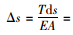
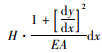
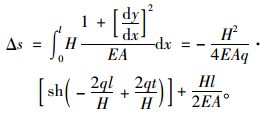
|
(2) |
(3) 主缆无应力长度计算
对于每一段单元有:
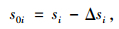
|
(3) |
因而可积分得到主缆无应力总长度为:
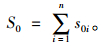
|
(4) |
上述公式中:S0为主缆无应力总长度; s0为索段无应力长度; s为索段有应力索长; Δs为索段伸长量; ds为索段x坐标处的微分单元; dx、dy分别是索段x坐标处的水平及竖向增量; l为索段两端点跨度; t为索段两端点高差; q为索段的单位质量; T为索段的轴向索力; H为索段的水平分力; A为主缆的截面面积; E为主缆钢丝的弹性模量。
通过有限元模型计算时,在进行成桥平衡状态分析得到主缆成桥线形和主缆张力后,扣除伸长量即得到无应力索长。
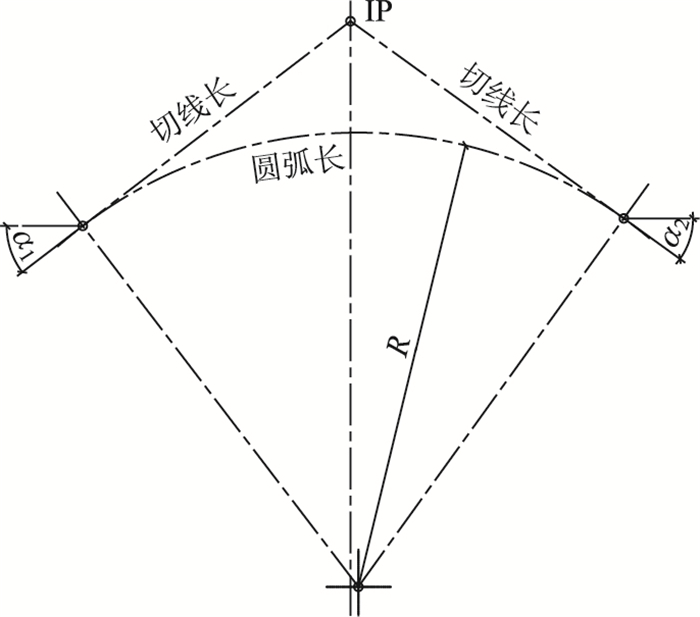
3.2 索股长度修正计算主缆无应力长度求解得到理论计算值后,每根索股的无应力长度则需要进行修正计算。由于主缆一般采用中心索股进行计算,索股长度计算在塔顶采用IP尖点而非沿索鞍弯曲, 如图 6所示。因此对于中心索股仅需要对塔顶索鞍处进行长度修正计算[8]。相对于中心索股的主缆其他索股,由于在塔顶索鞍处弯曲半径不同、散索后锚固跨空间差异以及垂度差别的影响,需要逐段进行修正计算。将主缆按控制点分为锚固点到散索鞍段、边跨曲线段、塔顶索鞍曲线段和中跨曲线段分别计算,然后将各段的无应力索长相加得出全桥主缆各束股的计算长度[9]。
|
| 图 6 塔顶索鞍圆弧处索长修正示意图 Fig. 6 Schematic diagram of revision of cable length at circular segment of saddle of pylon top |
| |
(1) 锚固点到散索鞍索长。由于该区段索股在横竖向都进行散开,同时每一层索股离开散索鞍的脱离点都不相同,因此该区段索股长度的计算比较复杂。根据该区段的中心索股长度,先对锚垫板到散索鞍的各索股空间关系进行索股长度修正,再根据不同层脱离点位置进行修正。
(2) 散索鞍到主索鞍切点段索长。该区段索股互相平行,但由于散索鞍到主索鞍切点的主缆转角发生变化,因此相对于中心索股,其他索股长度应进行相应修正。
(3) 主索鞍座索段的索长。该区段索股均为同心圆,因此其他索股依据中心索股长度按照几何关系修正即可。
(4) 中跨主索鞍两切点间索长计算。计算方法与边跨散索鞍到主索鞍切点段索长修正方法相同。
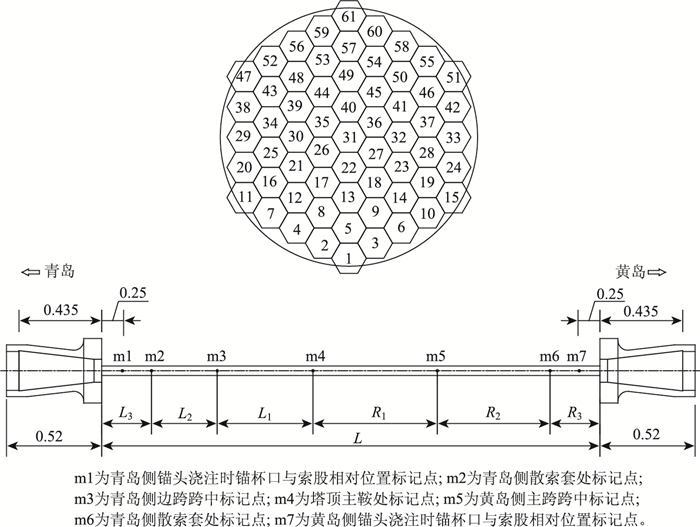
图 7为主缆索股编号及标记点示意图,表 2为主缆部分索股无应力索长计算结果。
|
| 图 7 主缆索股编号及标记位置(单位:m) Fig. 7 Strands number and relevant marker positions (unit:m) |
| |
| 索股编号 | L3 ① | L2 ② | L1 ③ | R1 ④ | R2 ⑤ | R3 ⑥ | L |
| 1 | 17.360 | 88.398 | 115.089 | 150.100 | 118.324 | 17.263 | 506.534 |
| 29 | 17.220 | 88.377 | 115.193 | 150.181 | 118.284 | 17.207 | 506.462 |
| 31 | 17.202 | 88.377 | 115.193 | 150.181 | 118.284 | 17.095 | 506.332 |
| 33 | 17.186 | 88.377 | 115.193 | 150.181 | 118.284 | 17.217 | 506.438 |
| 61 | 17.429 | 88.356 | 115.297 | 150.261 | 118.244 | 17.312 | 506.899 |
在主缆索股制造时,按照上述计算结果对标记点进行标记,以便缆索安装时进行控制。如果个别索股安装索力测试装置,则应在L3和R3段增加索股长度进行补偿。L3和R3还包括无应力长度预留量(该桥为5 cm),在索股架设时采用调整垫板通过索长预留量进行线形调整,保证空缆线形最大限度满足要求。在该桥实际控制中,调整垫板实际厚度均在(50±5) mm,说明计算数据非常准确。
4 主索鞍预偏量计算由于空缆状态时,若主索鞍位于索塔中心线,主、边跨水平力差异巨大,这对此时仅有较小的主缆竖向分力作用下的索塔受力极为不利。将主索鞍向边跨侧偏移一定的距离(一般情况吊杆安装张拉时主跨主缆水平分力增量较大),使空缆状态时索鞍两侧主缆水平分力相等,主索鞍在纵桥向相对于索塔中心线偏移的距离就是索鞍预偏量[10-12]。
在有限元模型中,主缆空挂状态下,解除主缆与塔顶连接的纵桥向约束,主缆自动寻找平衡状态,使得索鞍两侧主缆水平分力相等,此时主缆节点发生偏向边跨的位移,该值即为索鞍预偏量。在该索鞍预偏状态下的主缆线形才是空缆线形。注意,此时索塔偏心受压,将发生较小的纵桥向位移,因此索鞍中心点位置为索鞍预偏量与塔顶偏移量之和。
5 索夹预偏量计算对于空间缆,相对于成桥状态,空缆状态索夹的坐标和横向转角都发生了一定的变化,而空缆状态主缆位置已经确定,在主缆上通过纵桥向坐标即可确定索夹位置。因此,索夹预偏包含纵桥向坐标预偏和横桥向角度预偏。纵桥向坐标预偏较易计算,求得空缆线形,缆上吊点位置即索夹位置,实际控制时通过吊点纵坐标即找到索夹安装位置。而索夹角度预偏则难以计算,目前国内外对自锚式悬索桥的索夹横向预偏角度的研究经验和文献资料尤为缺乏[13],通常可通过模型试验进行实测确定。
对于有限元分析,得到空缆线形即得到索夹坐标,但是由于桁架或索单元扭转问题无法计算,因此索夹横向偏转角度则计算不出来。这里给出近似计算方法如下:将主缆索单元替换为相同截面特性的梁单元,并在索夹节点处建立虚拟刚臂,通过吊杆的张拉,主缆单元带动虚拟刚臂出现横向偏转,此偏转角度即为索夹横向偏转角度,按此值进行索夹的角度预偏,从而保证成桥时索夹与吊杆处于同一平面。表 3为空缆状态时索夹的坐标及预偏角度计算结果。在实桥控制时,应注意对加劲梁架设造成的吊点纵桥向坐标偏差进行修正。
| 边跨 | 主跨 | |||||
| 索夹编号 | 纵坐标/m | 横向预偏角度/(°) | 索夹编号 | 纵坐标/ m | 横向预偏角度/(°) | |
| B1 | 515.677 | 2.1 | 索塔中心 | 659.980 | ||
| B2 | 527.524 | 1.8 | Z1 | 671.924 | 1.5 | |
| B3 | 539.392 | 1.7 | Z2 | 684.223 | 1.3 | |
| B4 | 551.291 | 1.5 | Z3 | 696.480 | 1.1 | |
| B5 | 563.225 | 1.5 | Z4 | 708.694 | 1.0 | |
| B6 | 575.173 | 1.4 | Z5 | 720.872 | 0.8 | |
| B7 | 587.156 | 1.4 | Z6 | 733.015 | 0.6 | |
| B8 | 599.174 | 1.4 | Z7 | 745.108 | 0.5 | |
| B9 | 611.213 | 1.5 | Z8 | 757.196 | 0.4 | |
| B10 | 623.274 | 1.5 | Z9 | 769.228 | 0.3 | |
| B11 | 635.379 | 1.5 | Z10 | 781.229 | 0.3 | |
| B12 | 647.519 | 1.6 | Z11 | 793.196 | 0.3 | |
| 索塔中心 | 659.980 | - | Z12 | 805.116 | 0.4 | |
| Z13 | 817.035 | 0.6 | ||||
| Z14 | 828.926 | 1.0 | ||||
| Z15 | 840.789 | 1.6 | ||||
| Z16 | 852.641 | 2.8 | ||||
| Z17 | 864.471 | 4.9 | ||||
6 结论
(1) 综合倒装-正装-无应力状态法的施工控制方法,可在成桥平衡状态基础上精确计算主缆空缆线形,保证在与桥梁施工相同的正装模型上最终主缆线形与设计线形一致。
(2) 施工阶段计算必须精确模拟主索鞍与主缆切点的变化以及散索鞍至锚固点的散索情况,否则主缆在主索鞍及散索鞍附近坐标与实际情况偏差较大。
(3) 主缆无应力索长通过在成桥平衡状态主缆各索段长度基础上扣除弹性伸长量计算得到,中心索股需对主索鞍曲线索段进行修正,其他索股还需对散索段和主边跨曲线段进行修正计算。
(4) 主索鞍预偏通过空缆状态解除索鞍纵桥向约束使得索鞍自由滑动偏出索塔中心线一定位移求得,此时两侧主缆水平分力相等,桥塔受力安全。
(5) 索夹预偏包含纵桥向坐标预偏和横向角度预偏。索夹坐标预偏通过空缆状态索夹节点坐标得到,横向角度预偏则需要进行模型试验或采用单元替换方式计算得到。
| [1] | 王鹏, 吴迅. 悬索桥空缆线形计算[J]. 结构工程师 , 2005, 21 (6) : 22-27 WANG Peng, WU Xun. Analysis of Cable Shape of Suspension Bridge at Cable Finished Stage[J]. Structural Engineers , 2005, 21 (6) : 22-27 |
| [2] | 唐茂林, 沈锐利, 强士中. 大跨度悬索桥丝股架设线形计算的精确方法[J]. 西南交通大学学报 , 2001, 36 (3) : 303-307 TANG Mao-lin, SHEN Rui-li, QIANG Shi-zhong. An Accurate Calculation Method for Erecting Curves of Wire Strands of Long Suspension Bridges[J]. Journal of Southwest Jiaotong University , 2001, 36 (3) : 303-307 |
| [3] | 李小珍, 胡大琳, 陈祥宝. 大跨度悬索桥施工状态的计算机仿真分析[J]. 中国公路学报 , 1998, 11 (4) : 67-72 LI Xiao-zhen, HU Da-lin, CHEN Xiang-bao. Computer Simulation Analysis of Long Span Suspension Bridge's Construction State[J]. China Journal of Highway and Transport , 1998, 11 (4) : 67-72 |
| [4] | 魏家乐.大节段吊装施工的自锚式悬索桥施工控制仿真分析及关键技术[D].西安:长安大学, 2010. WEI Jia-le.Simulation and Key Technologies for Construction Control of Self-anchor Suspension Bridge with Large Segment Hoisting Construction[D].Xi'an:Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220896.htm |
| [5] | 向中富, 徐君兰, 代正宏. 悬索桥施工控制分析的恒定无应力索长迭代法[J]. 重庆交通学院学报 , 2000, 19 (3) : 16-21 XIANG Zhong-fu, XU Jun-lan, DAI Zheng-hong. The Alternate Calculation Method of Constant Cable-length in Non-stress for the Structural Analysis of Suspension Bridges[J]. Journal of Chongqing Jiaotong University , 2000, 19 (3) : 16-21 |
| [6] | 潘永仁, 范立础. 悬链线单元在悬索桥主缆下料长度计算中的应用[J]. 工程施工 , 1998 (3) : 20-24, 46 PAN Yong-ren, FAN Li-chu. Application of Catenary Element to Calculating the Fabrication Length of the Main Cable of Suspension Bridges[J]. Structural Engineers , 1998 (3) : 20-24, 46 |
| [7] | 李子奇, 樊燕燕. 自锚式悬索桥主缆无应力长度的计算分析研究[J]. 城市道桥与防洪 , 2007, 12 (12) : 91-94, 119 LI Zi-qi, FAN Yan-yan. Calculation Analysis and Study of Un-stressing Length of Main Cable for Self-anchored Suspension Bridge[J]. Urban Roads Bridges & Flood Control , 2007, 12 (12) : 91-94, 119 |
| [8] | JAYARAMAN H B, KNUDSON W C. A Curved Element for the Analysis of Cable Structures[J]. Computers and Structures , 1981, 14 (3) : 325-333 |
| [9] | 张哲. 混凝土自锚式悬索桥[M]. 北京: 人民交通出版社, 2005 . ZHANG Zhe. The Concrete Self-anchor Suspension Bridge[M]. Beijing: China Communications Press, 2005 . |
| [10] | 魏群, 严斌, 姜华. 大跨悬索桥主缆空缆线形的有限元分析与探讨[J]. 水利电力机械 , 2007, 29 (12) : 19-22, 27 WEI Qun, YAN Bin, JIANG Hua. FEA of the Main Cable of Large Span Suspension Bridge[J]. Water Conservancy & Electric Power Machinery , 2007, 29 (12) : 19-22, 27 |
| [11] | 李俊, 李雪红, 李枝军, 等. 独塔自锚式悬索桥主缆线形的计算方法[J]. 南京工业大学学报:自然科学版 , 2014, 36 (1) : 77-82 LI Jun, LI Xue-hong, LI Zhi-jun, et al. Calculation Method for Main Cable Curve on Single-pylon Self-anchored Suspension Bridge[J]. Journal of Nanjing University of Technology:National and Science Edition , 2014, 36 (1) : 77-82 |
| [12] | 狄谨, 武隽. 自锚式悬索桥主缆线形计算方法[J]. 交通运输工程学报 , 2004, 4 (3) : 38-43 DI Jin, WU Jun. Calculation Methods for Cable Curve of Self-anchored Suspension Bridge[J]. Journal of Traffic and Transportation Engineering , 2004, 4 (3) : 38-43 |
| [13] | 黄海云, 张俊平, 刘爱荣, 等. 空间索面自锚式悬索桥主缆横向位移及索夹横向偏转角的试验研究[J]. 公路工程 , 2009, 34 (2) : 41-44, 100 HUANG Hai-yun, ZHANG Jun-ping, LIU Ai-rong, et al. Testing Study on Lateral Displacement of Main Cable and Lateral Deflection Angle of Cable Clamp in the Self-anchored Suspension Bridge with Spatial Cable System[J]. Highway Engineering , 2009, 34 (2) : 41-44, 100 |
 2016, Vol. 33
2016, Vol. 33
