扩展功能
文章信息
- 袁明, 袁晟, 颜东煌
- YUAN Ming, YUAN Sheng, YAN Dong-huang
- 预应力混凝土箱梁塑性损伤分析
- Analysis on Plastic Damage of Prestressed Concrete Box Girder
- 公路交通科技, 2016, 33(11): 86-92
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 86-92
- 10.3969/j.issn.1002-0268.2016.11.013
-
文章历史
- 收稿日期: 2015-12-30
随着我国交通量的不断增加,在役公路桥梁的运营荷载大大超出了设计荷载等级,加之环境等自然因素的不断侵蚀作用,现有桥梁安全事故时有发生。混凝土梁桥在既有桥梁中占据了大量的比例,在日益增长的交通荷载与腐蚀环境因素作用下,既有混凝土桥梁均出现不同程度的损伤和裂缝,预应力混凝土箱梁结构具有诸多优势,而腹板开裂问题则是其一直存在且亟待解决的问题[1-2],这些病害直接影响到桥梁的整体刚度和承载力。对混凝土梁桥开裂损伤及承载能力的准确模拟能够为现有桥梁的安全评估与维修加固等措施提供一定的理论依据。
对于一般的混凝土结构设计,多是以弹性分析为主,而并未对其开裂后的非线性特性做过多考察。针对混凝土结构的非线性模拟方法,目前主要是采用刚塑性极限方法、弹塑性截面方法和非线性有限元分析方法等[3]。非线性有限元方法在复杂结构受力状态下的结构内力与变形发展, 以及裂缝的形成与发展等方面具有一定的适用性以及分析精度。在此,常用的混凝土本构模型主要有弥散裂缝模型、塑性损伤模型以及弹性断裂模型[4]。文献[5]的研究结果表明,弥散裂缝模型的受压弹塑性本构相对比较简单,且仅适合于由受拉开裂引起的低围压混凝土构件;塑性损伤将非关联硬化引入混凝土弹塑性本构中,对单向受力、循环受力及动态受力等情况都适用;两种模型都能对单调荷载作用下混凝土结构的宏观反应进行准确的模拟;由于预应力的存在,预应力筋与混凝土的黏结处存在高度非线性,塑性损伤模型在此具有较好的收敛性及适用性。目前,将非线性有限元与混凝土塑性损伤模型相结合用以分析预应力混凝土箱梁非线性响应的研究成果相对较少。
为了准确模拟预应力混凝土箱梁在单调荷载作用下的极限承载能力及其开裂损伤状态,本文采用非线性有限元方法, 基于塑性损伤模型, 对某预应力混凝土试验箱梁进行数值分析, 并将模拟结果与试验数据进行对比验证。研究结果表明将损伤因子引入预应力混凝土箱梁的非线性分析方法可行,且能准确地获取结构抗弯抗剪性能及破坏特征,单调荷载作用下有无损伤因子对结构极限承载能力有较大的影响, 而采用何种损伤因子计算方法对结果影响不大。
1 混凝土塑性损伤模型塑性损伤模型是由Lubliner等提出,并由Lee和Fenves进行了改进和发展[5],用以模拟混凝土、砂浆等准脆性材料在反复荷载作用下的力学行为。该模型采用有效应力和硬化变量来描述,表达式为:
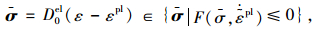
|
(1) |
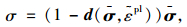
|
(2) |
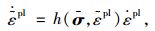
|
(3) |
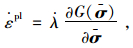
|
(4) |
式(1)定义了有效应力和弹性应变之间的关系,σ为有效应力张量; D0el为初始(无损伤)
弹性刚度; 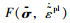
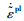
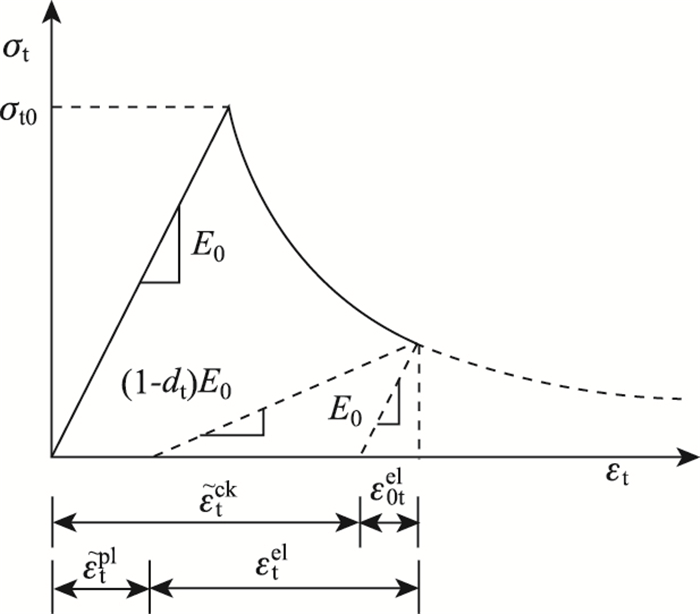
单轴受拉时,在达到失效应力σt0之前为线弹性,用弹性模量E0(初始弹性模量)来描述其力学行为,之后为软化阶段,同时伴随着刚度的退化,描述为后续的破坏应力和开裂应变的关系。如图 1所示,由
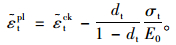
|
(5) |
|
图 1 混凝土单轴受拉应力应变曲线
Fig. 1 Stress-strain curve of concrete under uniaxial tension
注:σt, σt0-混凝土受拉应力和弹性最大受拉应力;ε0tel,εelt-无损伤的混凝土受拉弹性应变和考虑损伤的混凝土受拉弹性应变;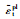 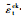 |
| |
单轴压缩时,在达到初始屈服应力σc0之前为线弹性,之后为强化阶段,直到极限应力σcu,然后为软化阶段。其中硬化数据由非弹性应变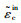
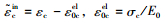
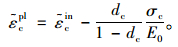
|
(6) |
|
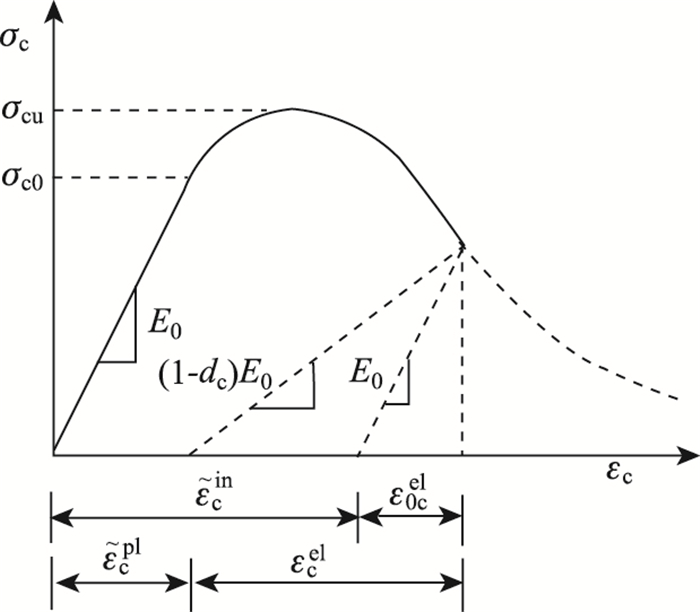
图 2 混凝土单轴受压应力应变曲线
Fig. 2 Stress-strain curve of concrete under uniaxial compression
注:σc, σc0, σcu-混凝土受压应力、弹性最大受压应力及最大受压应力;ε0cel,εelc-无损伤的混凝土受压弹性应变和考虑损伤的混凝土受压弹性应变;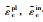 |
| |
因此,受拉受压的应力-应变关系可分别表示为:
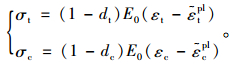
|
(7) |
该模型以损失指标dc和dt来分别描述混凝土在受压、受拉时损伤引起的弹性刚度退化,即
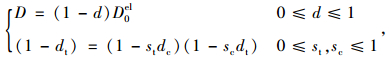
|
(8) |
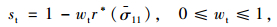
|
(9) |
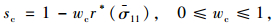
|
(10) |
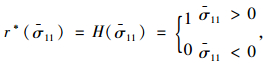
|
(11) |
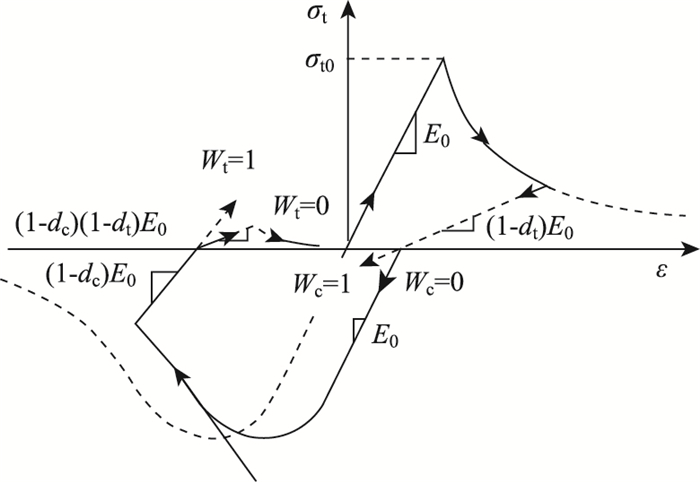
式中st,sc为应力反向刚度恢复时的应力状态函数;wc和wt为权重因子,与材料特性有关,用来描述材料在反向荷载作用下刚度的恢复程度,默认刚度恢复系数Wt=1(受压刚度完全恢复),Wc=0(受拉刚度不恢复),如图 3所示。
|
| 图 3 单轴循环荷载作用下应力-应变关系 Fig. 3 Stress-strain relationship under uniaxial cyclic loading 注:dc, dt-混凝土受压、受拉损伤因子。 |
| |
由式(1)~(11)即可得出以损失指标dc和dt来分别描述混凝土在受压、受拉时损伤引起的弹性刚度退化的塑性损伤模型。
2 模型参数选取 2.1 应力-应变曲线为了将模型应用于实际模拟分析中,结合混凝土结构设计规范给出了该模型应力-应变关系具体参数的确定方法。CDP模型的应力-应变关系选用规范[6]给出的混凝土本构关系,弹性阶段的应力应变关系通过定义材料的杨氏模量E和极限弹性应力σt0(σc0)来实现,非弹性阶段的应力-应变关系采用规范提供的混凝土应力-应变关系确定。受拉与受压状态下的表达式分别为:
受拉状态下:
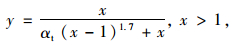
|
(12) |
式中x=ε/εt,y=σ/ft,αt为单轴受拉应力应变曲线下降段参数值。
受压状态下:
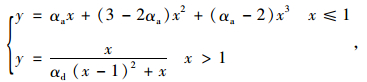
|
(13) |
式中, x=ε/εc,y=σ/fc,αa和αd分别为单轴受压应力应变曲线上升段及下降段参数值。
对于描述模型弹性阶段的杨氏模量的取值问题,由于混凝土受压初始阶段以及受拉阶段可认为混凝土处于弹性阶段,考虑到CDP模型采用的是等向强化模型,根据规范提供的混凝土本构关系,以受压应力应变曲线为例,取0.7σc时的割线模量作为混凝土初始弹性模量,泊松比采用规范推荐值0.2。
2.2 损伤因子国内外学者就其损伤因子的计算采用了不同的方法[7-10]且都取得了很好的结果,由于文献[9]中相关参数未做明确规定,本文采用文献[9]和文献[10]中公式计算损伤因子, 并与无损伤因子分别用于计算。
方法1:文献[9]中单轴受压和受拉时损伤因子计算公式分别为:
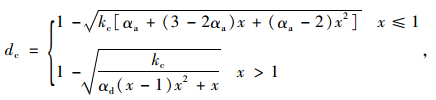
|
(14) |
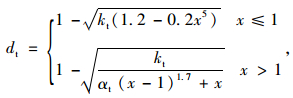
|
(15) |
式中,kc=fc/(εcE0),kt=ft/(εtE0)。
方法2:文献[10]中单轴受压和受拉时损伤因子计算公式:
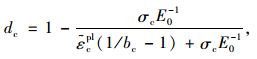
|
(16) |
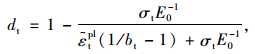
|
(17) |
式中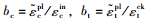
损伤塑性模型对于参数的取值对计算结果的收敛性影响很大,关于膨胀角φ和黏滞系数μ的取值都值得反复推敲。Abaqus手册[3]中默认采用36.31°,文献[11]建议膨胀角φ取35°,并指出其值对结果影响不大。文献[12]研究表明,黏滞系数取值过大,结构有变“刚”的趋势,会增大其极限承载力,取值过小收敛将会很困难,本文取为0.001取得较为理想的结果。
| φ | ε | σb0/σc0 | Kc | μ |
| 35 | 0.1 | 1.16 | 0.667 | 0.001 |
| 注:φ为膨胀角;ε为流动势偏移量;σb0/σc0为双轴极限抗压强度与单轴受压极限强度之比;Kc为拉伸子午面上与压缩子午面上的第二应力不变量之比;μ为黏滞系数。 | ||||
3 数值分析 3.1 预应力混凝土箱梁模型
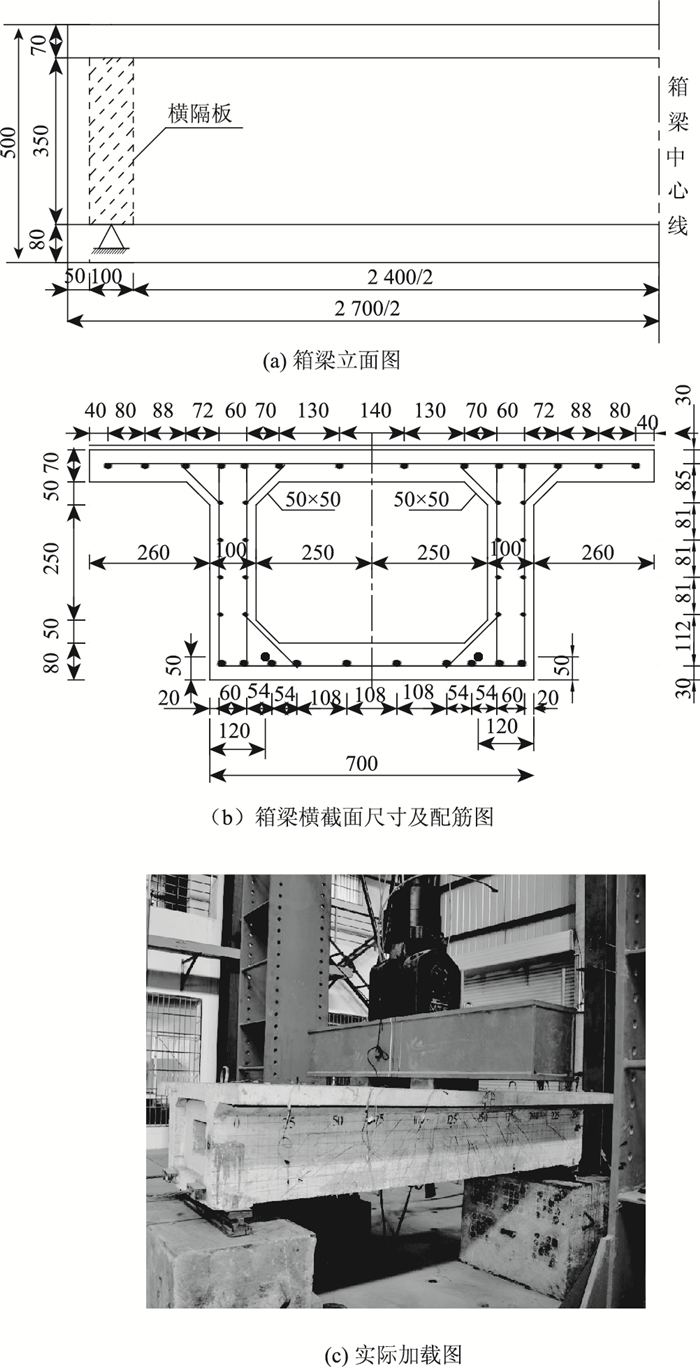
试验梁具体截面尺寸及钢筋详细配置如图 4所示,浇注混凝土强度等级采用C50,采用GMA无收缩自流密实型混凝土外加剂和42.5号水泥进行预应力孔道压浆,比例为1:4,其水灰比1:0.26。考虑到实际桥梁受力要求,试验梁按弯曲破坏进行设计并配筋。箍筋采用直径为6 mm的HRB400钢筋;顶板普通纵向筋采用直径8 mm的HRB400钢筋;腹板普通纵向筋采用直径6 mm的HRB400钢筋;底板按照要求布置于直径10 mm的HRB400钢筋;构造筋使用直径6 mm的R235钢筋;纵向预应力筋使用直径为15.2 mm (1×7)的钢绞线,距离箱梁底部50 mm,一次超张拉锚固,预应力值取为1 116 MPa。
|
| 图 4 箱梁截面尺寸(单位:mm) Fig. 4 Cross-section dimensions of box girder (unit: mm) |
| |
3.2 有限元模型
基于abaqus按实际尺寸建立精细化数值模型,混凝土和普通钢筋及预应力筋分别采用C3D8R单元和T3D2单元建立分离式模型,并采用ABAQUS的“嵌入”方法进行自由度耦合,模拟钢筋与混凝土间的相互作用。此方法模拟钢筋与混凝土的黏结滑移尚显不足。
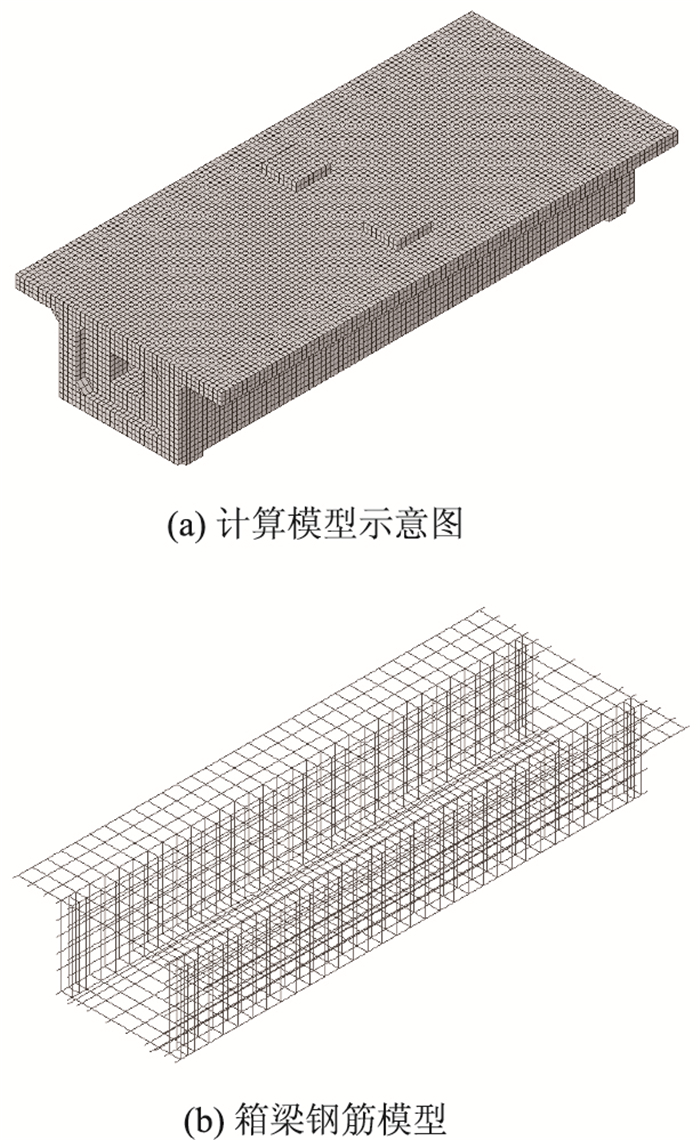
同时计算模型中设置了刚性垫块,建立参考点与加载面耦合起来,以防止加载点与支座处因为应力集中导致局部损坏。从试验结果来看,横隔板具有足够的强度而未出现裂缝,因此给其定义为弹性材料。试验梁有限元模型如图 5所示。
|
| 图 5 箱梁有限元模型 Fig. 5 Finite element model of box girder |
| |
计算中采用的钢筋参数见表 2,预应力筋采用弹性材料,其弹模取195 MPa。基于试验数据,钢筋采用2折线强化模型,强化段弹性模量取初始弹性模量的1/100。混凝土材料取C50,初始弹性模量取为29.47 GPa,泊松比取为0.2,受压屈服强度σc0=22.68 MPa,极限抗压强度σcu=32.4 MPa,极限抗拉强度σt0=2.64 MPa,其软化段数据根据第2节公式(12)~(15)确定,其余具体参数如前所述。
| 钢筋类别 | 构造钢筋 | 纵筋及箍筋 | ||
| 直径/mm | 6 | 6 | 8 | 10 |
| 屈服强度/MPa | 326 | 463 | 481 | 474 |
| 极限强度/MPa | 459 | 682 | 673 | 651 |
| 初始弹性模量/GPa | 210 | 200 | 200 | 200 |
3.3 分析结果
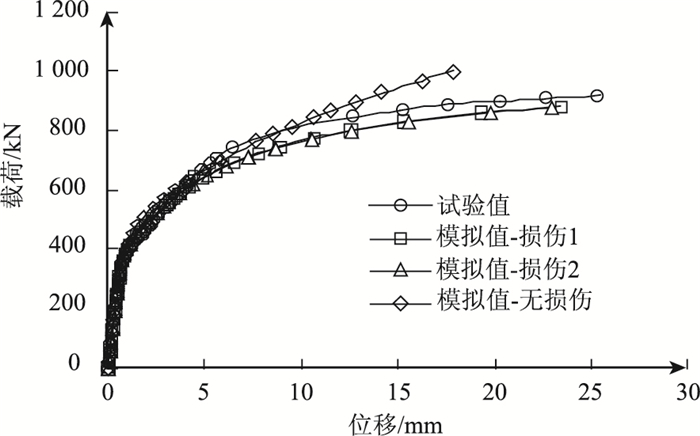
计算主要模拟跨中单向荷载作用下试验梁极限承载力及其开裂损伤状态,将采用方法1、方法2以及无损本构数据计算得到的荷载-位移曲线与试验得到的荷载-位移曲线进行对比,如图 6所示。从图中可以看出,方法1与方法2计算所得曲线基本重合且与试验测得的曲线在弹性段及强化段初期吻合较好,后期刚度较实际偏低,这是因为钢筋强化段与实际存在差别,但后期曲线变化趋势基本一致。计算开裂荷载为330 kN,试验开裂荷载为350 kN,达到试验值的94.3%。方法1计算所得极限承载力为879.9 kN (顶板混凝土达到极限抗压强度),达到实际梁体承载力918 kN的95.8%,方法2计算所得极限承载力为875.84 kN,达到试验值的95.4%;而未添加损伤因子的计算结果则显示其极限承载力明显高于试验值,且后期变化趋势与试验结果并不吻合。这说明塑性损伤模型在单向荷载作用下的结构计算中,损伤因子的取舍对计算结果影响较大,加损伤因子能更好地模拟实际结构,且计算结果可靠度高,至于采用常用的哪种损伤因子计算方法,结果显示并无太大区别,反复荷载作用下的结构响应及区别还有待进一步研究。
|
| 图 6 计算荷载-位移曲线与试验曲线对比图 Fig. 6 Comparison of load displacement between calculated curves and experimental curve |
| |
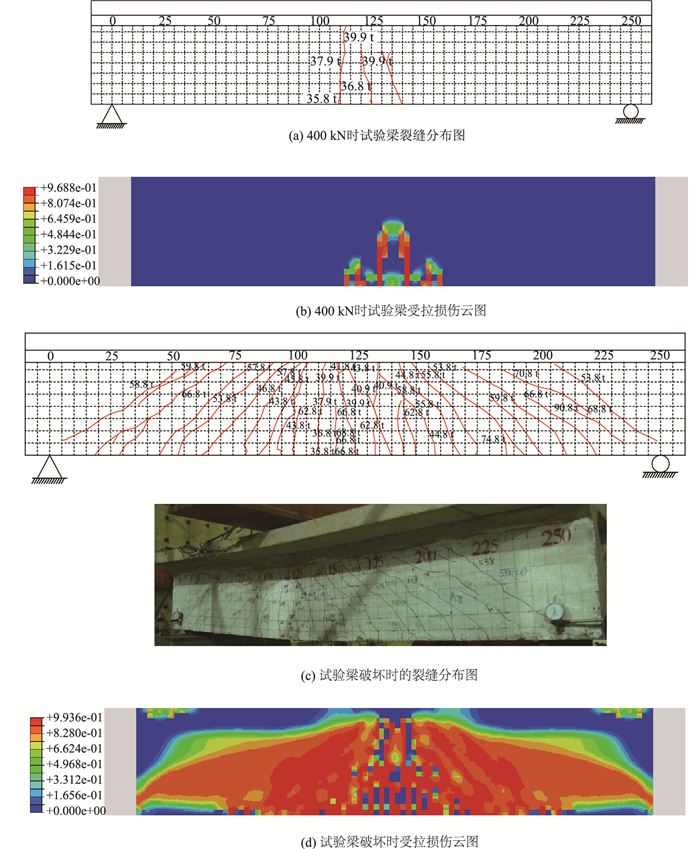
对于裂缝,塑性损伤模型无法显示积分点上裂缝的发展,但由于混凝土开裂后即出现拉伸损伤,故可根据拉伸损伤值来表示裂缝分布区域。以下选取方法1计算结果与试验结果进行对比分析如图 7所示, 图中分别列举了施加400 kN及试验梁破坏时梁体损伤与试验裂缝分布对比图。
|
| 图 7 计算受拉损伤云图与试验裂缝分布对比图 Fig. 7 Comparison of calculated nephogram of tensile damage and experimental crack distribution |
| |
从图 7中可以看出,拉伸损伤位置与试验梁实际开裂位置吻合得较好。由图(a)与(b)可知,试验及计算模拟表明箱梁最先于跨中出现弯曲裂缝,并随着荷载增加,裂缝开始倾斜,计算结果也出现斜向损伤值;由图(c)与(d)可知箱梁破坏时出现大量弯曲裂缝及斜裂缝,而裂缝分布区域与拉伸损伤区域吻合较好。
5 结论本文基于混凝土塑性损伤模型的基本理论与规范所示混凝土本构关系,采用非线性有限元对预应力混凝土箱梁进行了承载力计算及塑性损伤分析,主要得出以下结论:
(1) 在规范提供的本构基础上,引入损伤因子的塑性损伤模型对预应力混凝土箱梁的非线性分析方法可行,且能准确获取结构抗弯抗剪性能及其破坏失效过程。
(2) 单调荷载作用下有无损伤因子对结果影响较大,采用哪种损伤因子计算方法对结果影响不明显,以损伤因子表征结构损伤发展切实可行。
(3) 同时也存在不能定量得知单元开裂比例,膨胀角、黏滞系数等参数的设置需根据试验结果来选择等不足之处,重复荷载作用下预应力混凝土箱梁结构的响应亦有待进一步研究。
| [1] | 钟新谷. 预应力混凝土连续箱梁桥裂缝防治与研究[J]. 铁道科学与工程学报 , 2006, 3 (3) : 7-14 ZHONG Xin-gu. Analysis and Prevention of the Cracks in Continuous Prestressed Concrete Box-girder Bridges[J]. Journal of Railway Science and Engineering , 2006, 3 (3) : 7-14 |
| [2] | 王国亮, 谢峻, 傅宇方. 在用大跨度预应力混凝土箱梁桥裂缝调查研究[J]. 公路交通科技 , 2008, 25 (8) : 52-56 WANG Guo-liang, XIE Jun, FU Yu-fang. Investigation Research on Crack of Long-span Prestressed Concrete Box Girder Bridges in Service[J]. Journal of Highway and Transportation Research and Development , 2008, 25 (8) : 52-56 |
| [3] | 徐秉业, 刘信声. 结构塑性极限分析[M]. 北京: 中国建筑工业出版社, 1985 . XU bing-ye, LIU Xin-sheng. Analysis on Plastic Limit of Structure[M]. Beijing: China Architecture and Building Press, 1985 . |
| [4] | 江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005 . JIANG Jian-jing, LU Xin-zheng, YE Lie-ping. Finite Element Analysis of Concrete Structures[M]. Beijing: Tsinghua University Press, 2005 . |
| [5] | ABAQUS Inc. ABAQUS User's Manual[M]. s.l:Ver. 6.7. ABAQUS Inc., 2007. |
| [6] | GB50010-2002, 混凝土结构设计规范[S]. GB50010-2002, Code for Design of Concrete Structures[S]. |
| [7] | 张劲, 王庆扬, 胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构 , 2008, 38 (8) : 127-130 ZHANG Jin, WANG Qing-yang, HU Shou-ying, et al. Parameters Verification of Concrete Damaged Plastic Model of ABAQUS[J]. Building Structure , 2008, 38 (8) : 127-130 |
| [8] | 郭明. 混凝土塑性损伤模型损伤因子研究及其应用[J]. 土木工程与管理学报 , 2011, 28 (3) : 128-132 GUO Ming. Research and Application of Damage Factor in Concrete Plastic-damage Model[J]. Journal of Civil Engineering and Management , 2011, 28 (3) : 128-132 |
| [9] | 曹明. ABAQUS损伤塑性模型损伤因子计算方法研究[J]. 交通标准化 , 2012 (2) : 51-54 CAO Ming. Research on Damage Plastic Calculation Method of ABAQUS Concrete Damaged Plasticity Model[J]. Transportation Standardization , 2012 (2) : 51-54 |
| [10] | BIRTEL V, MARK P. Parameterised Finite Element Modelling of RC Beam Shear Failure[C]//Proceedings of the 19th Annual International ABAQUS Users' Conference. Boston:[s. n.] 2006:95-108. |
| [11] | CHEN G M. Shear Behaviour and Strength of RC beams Shear-strengthened with Externally Bonded FRP Reinforcement[D]. Hong Kong:Hong Kong Polytechnic University, 2010. http://ira.lib.polyu.edu.hk/handle/10397/2537 |
| [12] | 彭小婕, 于安林, 方有珍. 混凝土损伤塑性模型的参数分析[J]. 苏州科技学院学报:工程技术版 , 2010, 23 (3) : 40-43 PENG Xiao-jie, YU an-lin, FANG You-zhen. An Analysis on Parameters for Concrete Damage Plasticity Model[J]. Journal of Suzhou University of Science and Technology:Engineering and Technology Edition , 2010, 23 (3) : 40-43 |
 2016, Vol. 33
2016, Vol. 33
