扩展功能
文章信息
- 李英超, 王树青, 石云
- LI Ying-chao, WANG Shu-qing, SHI Yun
- 基于不完备、含噪声模态参数的梁式结构损伤识别
- Identification of Damage in Beam Structures Based on Incomplete and Noise-polluted Modal Data
- 公路交通科技, 2016, 33(11): 76-85
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 76-85
- 10.3969/j.issn.1002-0268.2016.11.012
-
文章历史
- 收稿日期: 2016-01-29
2. 中国海洋大学 工程学院, 山东 青岛 266100
2. School of Engineering, Ocean University of China, Qingdao Shandong 266100, China
桥梁往往是交通运输的咽喉,一旦发生事故将造成不可估量的损失和社会影响。因此,及时监测桥梁结构的损伤,建立系统的安全评估体系,对于保障结构的安全运行至关重要[1]。基于振动测试的结构损伤诊断技术已成为该领域研究的一大重点[2-3]。近20年,学者们提出了很多种损伤识别方法,如模型修正法、敏感性分析法、神经网络法、遗传算法和模态应变能法等[4]。对比各类方法,模型修正法具有两大优点:(1)可同时识别损伤位置和损伤程度;(2)修正后的有限元模型可用于结构的安全评估[5]。然而传统的模型修正方法在实际应用中尚存在很多问题,如设计参数型方法需要迭代计算,其收敛性不能保证,而矩阵型方法通常缺乏物理意义,另外各类方法受实测信息量的影响均较大[6]。
针对传统模型修正方法的缺陷,Hu等[7]提出了交叉模型交叉模态(Cross-model Cross-mode,CMCM)方法。该方法综合了设计参数型方法和矩阵型方法的优点,计算过程无需迭代,且物理意义明确。另外,该方法最大的优点是不需要振型配对,即可以用有限的低阶实测模态构建更多的修正方程,从而能够求解更多的未知数。然而试验研究发现,该方法在实际应用中仍存在一些关键问题需要解决,如测量噪声影响下“病态”系统的求解问题和实测模态空间不完备问题等[8]。
线性“病态”系统在数学中最常用的求解方法是正则化方法。最早的正则化方法是由Tikhonov[9]提出的,它通过正则化参数的选择来控制解的振荡和方程的拟合程度。吴颉尔[10]对各种正则化方法进行了深入的对比研究,针对不同规模的“病态”系统推荐了适用的正则化方法。虽然正则化方法在理论上比较成熟,但在模型修正实际应用中仍然存在一些问题,如对于不同的方法、不同的问题,同一算法表现出的收敛性却不同,很难选择一种通用的方法[11]。因此,需要专门针对CMCM方程的特点,探讨对其适用的正则化求解方法。
解决实测模态空间不完备问题,最常用的手段是模态扩阶/模型缩阶,然而该过程往往会引入振型二次误差,从而导致损伤的漏判或误判。围绕CMCM方法,王俊荣[12]提出了一种实测模型从自由度修正法,该方法可有效避免扩阶/缩阶误差,可实现对有限元模型和实测模态的同时修正,然而在实际应用中其收敛性仍不能保证。Wang等[13-14]发展了一种基于频率信息的模态应变能迭代法,该方法可有效地避免振型的噪声误差和扩阶误差,且收敛性较好。本文借鉴该思路,给出了基于频率的迭代修正法用于处理实测模态空间不完备问题。
本文通过数值和试验算例将CMCM方法应用到桥梁结构的损伤识别中。重点针对测量噪声下“病态”系统的求解问题和实测模态不完备问题展开研究。结合CMCM方程组的求解特点,提出一种基于TSVD正则化[15-16]求解的模型修正过程,并通过算例验证该正则化方法的适用性。采用Guyan扩阶[17]和基于频率的迭代修正法两种技术来处理实测模态空间不完备问题,通过探讨优缺点,提出一种两阶段损伤识别过程,从而利用不完备、含噪声的模态参数识别桥梁结构的损伤。
1 基本理论 1.1 基于CMCM方法的损伤识别方法[7]在以下公式中,有“*”标记的表示与损伤结构相关的参数,无“*”标记的表示与无损伤结构相关的参数。
假定损伤结构的刚度矩阵K*和质量矩阵M*可表示为对无损伤结构刚度矩阵K和质量矩阵M的修正,即:
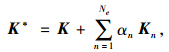
|
(1) |
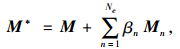
|
(2) |
式中,Kn和Mn为结构有限元模型第n个单元在整体坐标系下的刚度矩阵和质量矩阵;αn和βn为待求的刚度和质量修正系数,当-1≤αn < 0时表示该单元有损伤;Ne为待识别损伤的单元个数。
结构损伤前后特征值λi,λj*和特征向量Φi,Φj*的关系为:

|
(3) |
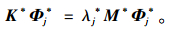
|
(4) |
用Φi的转置(Φi)T左乘式(4)得:
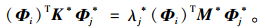
|
(5) |
将式(1)和式(2)代入式(5)得:
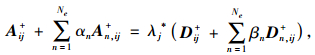
|
(6) |
式中,Aij+=(Φi)TKΦj*;An, ij+=(Φi)TKnΦj*;Dij+=(Φi)TMΦj*;Dn, ij+=(Φi)TMnΦj*。
将式(6)变形:
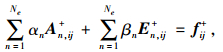
|
(7) |
式中,En, ij+=-λj*Dn, ij+,fij+=-Aij++λj*Dij+。
利用该方法进行损伤识别时,可假定结构质量不变,即M*=M。此时式(7)可写为:

|
(8) |
用Ni阶有限元模态和Nj阶实测模态,可以构建包含Nt=Ni×Nj个线性方程,将其写为矩阵形式:
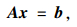
|
(9) |
式中,A为由An, ij+组成的Nt×Ne阶矩阵;x为包含Ne个修正系数αn(n=1, 2, 3, …, Ne)的列向量;b为由fij+组成的Nt×1阶列向量。求解式(9),即可实现对结构损伤的识别。
由于该方法采用了无损伤结构模态和有损伤结构模态的交叉乘积,方程组数目通常多于待识别单元的数目,即方程组为超定系统,可采用奇异值分解(SVD)法来寻求最小二乘解。对式(9)的系数矩阵A做奇异值分解:
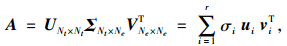
|
(10) |
式中,UNt×Nt和VNe×Ne为酉矩阵;ΣNt×Ne=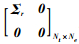
于是,方程组(9)的解xLS可写为:
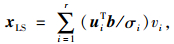
|
(11) |
式中,uiTb称为系数矩阵A的离散傅里叶系数[16]。
1.2 TSVD正则化求解方法“病态”性是各类模型修正方法面临的通病,CMCM方法也不例外。实测模态的测量噪声经常会导致最小二乘解远远偏离真实值,从而引起损伤的误判。
方程组的病态性及受噪声污染程度可以通过系数矩阵A的奇异值曲线(SVD曲线)和离散傅里叶系数曲线(Picard曲线)来衡量[14]。当SVD曲线在Picard曲线上方时,表示该方程组受噪声污染不严重;当完全位于下方或重合时即受噪声污染严重;介于两者之间时为一般严重。当方程组受噪声污染不严重或一般严重时,可利用一定的正则化方法来近似求解。
Tikhonov[9]正则化方法将最小二乘解‖b-Ax‖2和最小范数解‖x‖2平衡考虑:
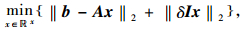
|
(12) |
式中,δ为正则化参数;I为单位矩阵。当δ较大时,可以保证‖x‖2值不会发生“振荡”,但可能会导致解不满足Ax=b;反之,如果δ较小,虽然能得到满足方程组的解,但该解会严重偏离真实值。根据这一原则,式(9)的正则解可写为:
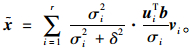
|
(13) |
正则化参数δ的作用是过滤掉小奇异值对解的贡献,从而使解稳定。
截断奇异值分解(TSVD)法[16]直接舍弃小奇异值对解的贡献,即取过滤因子为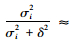
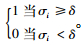
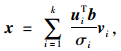
|
(14) |
式中k为截断数。
TSVD正则化方法的关键是截断数k的选择。对于截断数k∈(1, r),曲线ln (‖x‖2)和曲线ln (‖b-Ax‖2)的形状通常呈L型,其角点正好使得最小二乘解和最小范数解得到平衡,因此可通过该曲线的最大曲率来确定角点,从而来确定截断数k[16]。
1.3 实测模态空间不完备问题处理方法在模态测试中,受传感器数目的限制,实测模态往往是空间不完备的,本文介绍两种处理方法。
1.3.1 Guyan扩阶法[17]将结构的刚度矩阵K写为:
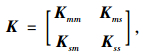
|
(15) |
式中,下标m表示与主自由度(测试自由度)相关的元素;s表示与从自由度(未测试自由度)相关的元素。
实测空间不完备振型可以通过转换矩阵得到扩展:
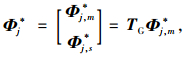
|
(16) |
式中,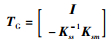
参考Wang等[13-14]提出的模态应变能迭代法,本文给出基于频率的迭代修正法。该方法由于只利用实测频率信息,可有效避免实测模态噪声和扩阶误差对损伤识别的影响,另外可同时实现对实测模态的扩阶和结构损伤的识别。具体步骤如下:
(1) 用初始有限元模型的刚度矩阵K(1)和质量矩阵M(1)计算振型Φj(1);
(2) 令实测模态Φj*(1)=Φj(1);
(3) 用Φj*(1)和实测频率信息λj*构建CMCM方程组,并进行求解,结果记为x(1);
(4) 用式(1)、式(2)对有限元模型进行修正,修正后的刚度矩阵和质量矩阵分别记为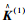
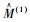
(5) 将修正后的模型作为下次修正的基准模型,令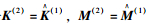
当迭代次数为m时,损伤识别结果为x=
对于CMCM方程组的解x=[α1 α2 … αNe]T,当-1≤αj < 0时表示第j单元有损伤。但是受振型扩阶和测量噪声的影响,修正解(损伤指标)α在非损伤单元位置上同样可能会出现非零解。因此将各单元的损伤指标α作为随机变量,并假定同样符合正态分布,利用统计假设检验[18],将αc=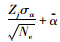
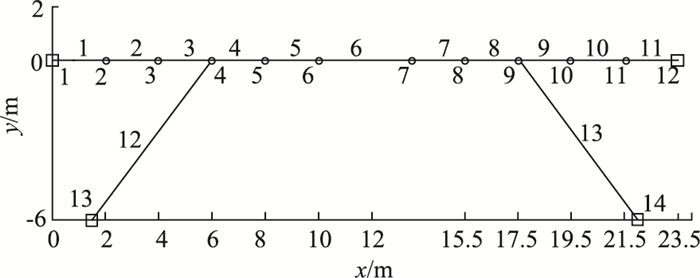
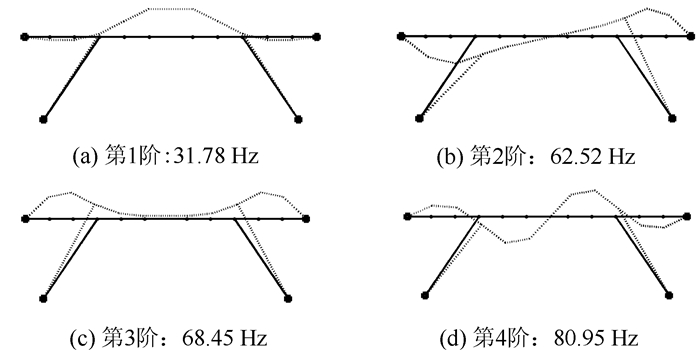
本文采用文献[19]中介绍的二维斜腿刚架桥模型进行数值研究。桥梁总长为23.5 m,材料密度为7 850 kg/m3,弹性模量为2.0×1011N/m2。横梁和腿柱分别选用美国AISC宽翼缘H型钢W36×135和W14×145。应用MATLAB编程,建立该结构的有限元模型,共包含14个节点,13个二维梁单元,如图 1所示。由于与文献[19]研究目的不同,本文将节点1和节点12简化为固定铰支座,将节点13和节点14简化为固定支座,因此该模型共有32个自由度。通过特征值分解,获得该模型的模态参数,如表 1和图 2所示。
|
| 图 1 桥梁结构有限元模型 Fig. 1 FE model of bridge structure |
| |
| 阶次 | FE模型(无损伤) | 损伤模型 | ||
| f/Hz | f/Hz | MAC/% | ||
| 1 | 31.78 | 30.08 | 99.96 | |
| 2 | 62.52 | 61.92 | 99.95 | |
| 3 | 68.45 | 67.59 | 99.91 | |
| 4 | 80.95 | 78.88 | 99.92 | |
| 注:MAC为实测模态与修正后有限元模型模态的置信度,下同。 | ||||
|
| 图 2 有限元(无损伤)模型振型图 Fig. 2 Mode shapes of FE (undamaged) model |
| |
结构的损伤通过单元刚度的折减来模拟。假定结构有单元4、单元6和单元9同时发生了损伤,损伤程度分别为30%,20%和15%。通过特征值分解得到损伤结构的模态参数。由于实际测试中仅能获得有限的低阶模态,因此本算例中假定仅前4阶模态可用,如表 1所示。
另外,为验证方法的适用性,分3种工况进行损伤识别研究:(1) 假定实测模态空间完备且不含噪声,用于检验CMCM方法的适用性;(2) 假定实测模态空间完备但包含噪声,探讨实测模态含噪声条件下CMCM病态方程组的求解问题;(3) 假定实测模态不完备且包含噪声,探讨Guyan扩阶和实测频率迭代修正法的适用性。最后,通过对比分析,给出两阶段损伤识别过程,并通过算例进行验证。
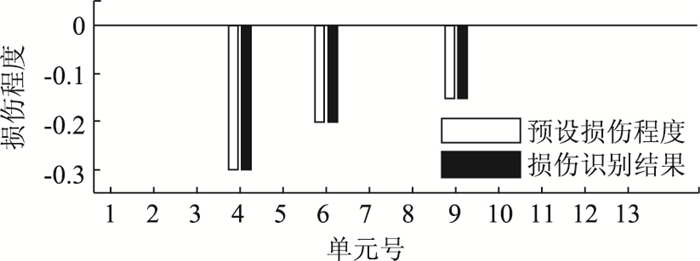
2.2 损伤识别 2.2.1 工况1:实测模态空间完备且不含噪声将结构的全部13个单元作为损伤识别的对象,利用结构损伤前后的前4阶模态构建16个CMCM方程,方程数大于未知数个数,利用式(11)所示SVD方法对方程组进行求解,结果如图 3所示。可以看出,当实测模态空间完备且不含噪声时,CMCM方法可以利用前4阶模态准确识别结构损伤。
|
| 图 3 工况1损伤识别结果 Fig. 3 Damage identification result of Case 1 |
| |
2.2.2 工况2:实测模态空间完备但包含噪声
根据模态测试经验,在有多测点信号相互校验的情况下,再借助一定的定阶消噪方法,模态频率的识别精度通常较高,测量噪声主要对模态振型产生较大影响。因此,文献[6-8]中只在振型上添加噪声,噪声添加方式为ϕi, j=ϕi, j(1+εRi, j),其中ε为噪声水平;Ri, j为均值为0、方差为1的高斯随机数;ϕi, j为对应于第i个自由度的第j阶振型值, 即在通过数值模拟获得的实测模态振型基础上添加一定水平的高斯白噪声。
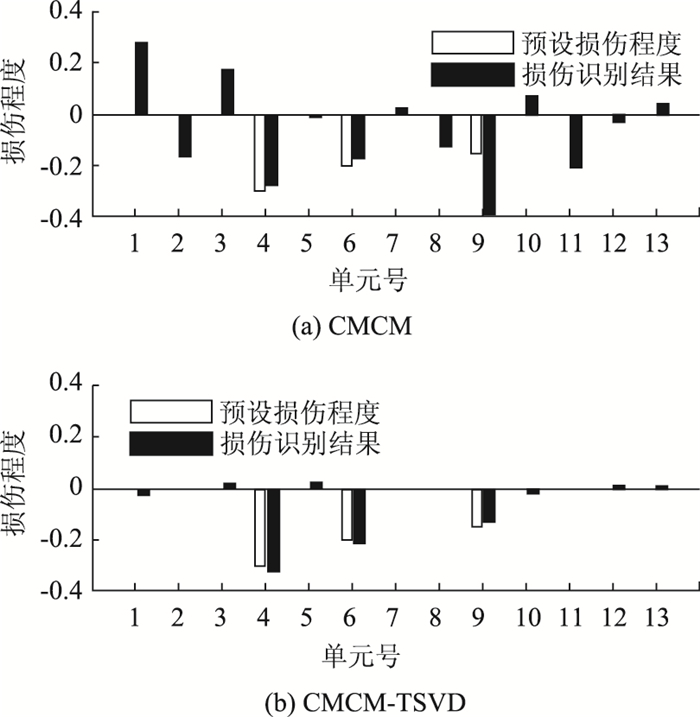
首先,假定噪声水平为1%。与工况1相同,构建16个CMCM方程,然后利用SVD法进行求解,结果如图 4(a)所示。可见,在测量噪声的影响下,结果远远偏离了真实解:(1) 损伤位置出现了误诊,如单元2,8和11;(2) 单元4,6和9的损伤程度识别误差较大。
|
| 图 4 工况2损伤识别结果(1%噪声水平) Fig. 4 Damage identification result of Case 2(1% noise level) |
| |
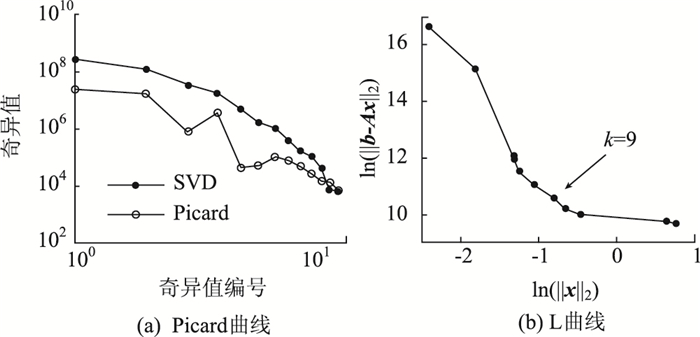
图 5(a)为CMCM方程的Picard曲线,可以看出,在噪声影响下,方程组的系数矩阵从第12个奇异值开始不能满足离散Picard条件。结合CMCM方程组求解特点,采用TSVD正则化方法进行求解。该系统的L曲线如图 5(b)所示,该曲线角点左侧第一个值对应k=9,将此作为截断数,然后根据式(14)求得该方程组的正则解,如图 4(b)所示。可以看出,基于TSVD正则化求解的CMCM方法(以下简称CMCM-TSVD方法)可以较准确地识别出单元4,6和9的损伤。
|
| 图 5 Picard和L曲线(工况2:1%噪声) Fig. 5 Picard and L curves (Case 2: 1% noise level) |
| |
为进一步探讨该方法的噪声鲁棒性,将损伤结构实测模态的噪声水平分别设为0.5%,1%,3%,5%和10%,然后分别利用CMCM方法和CMCM-TSVD方法进行损伤识别,结果如图 6所示。结合损伤阈值,提取各噪声水平下的损伤定位结果,如表 2所示。

|
| 图 6 工况2损伤识别结果(不同噪声水平) Fig. 6 Damage identification result of Case 2(different noise levels) |
| |
| 噪声水平/% | 0.5 | 1 | 3 | 5 | 10 | |
| CMCM方法 | 损伤指标阈值 | -0.054 | -0.063 | -0.042 | ||
| 损伤位置 | 4, 6, 8, 9 | 2, 4, 6, 8, 9, 11 | 无效 | 2, 4, 6, 8, 10, 11 | 无效 | |
| CMCM-TSVD方法 | 损伤指标阈值 | -0.054 | -0.055 | -0.065 | -0.050 | -0.062 |
| 损伤位置 | 4, 6, 9 | 4, 6, 9 | 4, 6, 8, 9 | 4, 6, 9, 10 | 2, 4, 6, 9, 10 | |
对比发现,利用传统的CMCM方法会出现对损伤的漏判(5%噪声时),并且损伤指标会出现小于-1的情况,失去物理意义(3%和10%噪声时)。而CMCM-TSVD方法体现出更强的鲁棒性,当实测模态噪声水平高达10%时,仍能够定位出预设损伤位置,无漏判情况发生。但随着噪声水平的提高,该方法对损伤程度的识别误差不断增大,如图 7所示。另外,当噪声水平较高时,也可能会出现虚假损伤。

|
| 图 7 不同噪声水平下的损伤识别误差 Fig. 7 Identification error of damage at different noise levels |
| |
2.2.3 工况3:实测模态空间不完备且包含噪声
假定在模态测试中仅能够获得2~11节点的y向振动信号,即仅能识别到10个自由度的振型值。本文采用Guyan扩阶方法和基于频率的迭代修正法对该问题进行对比研究。为模拟实际情况,同样将实测模态分别添加0.5%,1%,3%,5%和10%共5种噪声水平进行研究。
(1) 利用Guyan扩阶
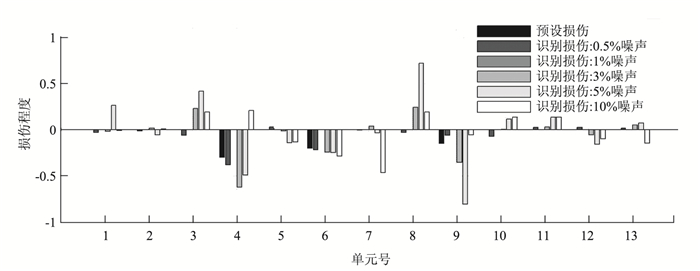
利用Guyan扩阶后的模态构建CMCM方程组,并采用TSVD方法进行求解(该过程简写为Guyan-CMCM-TSVD),结果如图 8所示。结合损伤阈值,提取各噪声水平下的损伤定位结果,如表 3所示。
|
| 图 8 工况3损伤识别结果(不同噪声水平) Fig. 8 Damage identification result of Case 3(different noise levels) |
| |
| 噪声水平/% | 0.5 | 1 | 3 | 5 | 10 |
| 指标指标阈值 | -0.066 | -0.064 | -0.065 | -0.061 | -0.05 |
| 损伤位置 | 4,6,9 | 4,6, 9,10 | 4,6,9 | 4,5,6,9,12 | 4,5,6,7,9,12,13 |
可见,该过程能有效地识别损伤位置,无漏判情况发生;但受振型扩阶和噪声的影响,会出现虚假损伤。另外由图 7对比结果看出,该工况对损伤程度的识别误差明显高于工况2,这说明Guyan扩阶会影响CMCM-TSVD方法对损伤程度的识别精度。
(2) 利用基于频率的迭代修正法
本部分尝试只用频率信息采用1.3.2介绍的迭代修正法进行损伤识别。
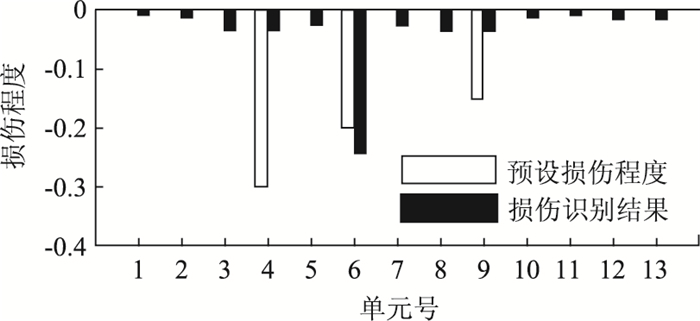
①将全部13个单元作为损伤识别对象,利用前4阶实测频率对无损伤模型进行迭代修正,结果发现很难收敛,当迭代次数为1 000次时,损伤识别结果如图 9所示,只有单元6的损伤得到准确识别,而其他单元的解偏离真值。主要原因是该过程中只有4个有效实测数据,而构建的方程需要求解13个刚度修正系数和全部4阶的模态振型,共计141个未知数,比较困难。
|
| 图 9 基于频率的迭代修正法损伤识别结果 Fig. 9 Damage identification result by iterative updating method based on frequencies |
| |
②假定损伤位置已确定,即将单元4、单元6和单元9作为损伤识别对象,经8次迭代,结果如图 11(a)所示,损伤程度得到精确的识别。原因是该过程未使用任何实测模态信息,从而避免了测量噪声以及扩阶造成的误差。

|
| 图 11 第Ⅱ阶段损伤识别结果(不同损伤定位情况) Fig. 11 Damage identification result of stage Ⅱ (for different damage locations) |
| |
2.2.4 两阶段损伤识别过程
对比工况2和工况3损伤识别结果可以看出,(1) 利用Guyan-CMCM-TSVD过程不会出现损伤漏判,但会有虚假损伤出现;另外,对损伤程度的识别误差较大。(2) 实测模态迭代修正法的收敛性受信息量影响较大,但在损伤位置得到初步定位的条件下,该方法可以较准确地识别损伤。
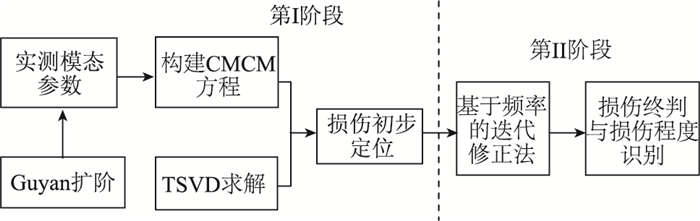
鉴于以上两种过程的优缺点,本文尝试采用一种两阶段过程对结构进行损伤识别,流程图如图 10所示。
|
| 图 10 两阶段损伤识别过程流程图 Fig. 10 Flowchart of 2-stage damage identification process |
| |
为验证该过程的有效性,将工况2中表 2和工况3中表 3所示结果作为第Ⅰ阶段的损伤定位结果。在此基础上,针对不同噪声水平下的损伤定位情况,采用基于频率的迭代修正法进行第Ⅱ阶段的损伤识别,结果如图 11所示。可见,即便在第Ⅰ阶段初步定位中出现虚假损伤,经过第Ⅱ阶段的迭代修正仍然可以很精确地识别出损伤的位置和程度,如图 11(b)~(f)所示。
3 悬臂梁试验算例悬臂结构是桥梁经常采用的结构形式之一。为验证本文所采用方法的有效性,对某悬臂梁物理模型开展损伤识别研究。
3.1 模型介绍该梁几何尺寸如图 12(b)所示,材料为钢材,弹性模量为2×1011 Pa,密度为7 850 kg/m3。其有限元模型如图 12(d)所示,共有11个节点,10个单元,节点1固定,(忽略梁的轴向变形)每个节点2个自由度,共20个自由度。通过特征值分解得到该梁有限元模型的模态频率和振型,如表 2所示。

|
| 图 12 悬臂梁模型 Fig. 12 Cantilever beam model |
| |
模态测试共包括无损伤和有损伤两种工况。其中损伤通过切割单元2来模拟,切割宽度为20 mm (约0.35倍的截面宽度),如图 12(a)所示。传感器布置方案如图 12(a)~(b)所示,只能测得各节点处切向自由度的加速度信号。测试仪器如图 12(c)所示。试验中,采用力锤敲击单元10的中间部位,模拟冲击激励,采集加速度响应信号,采样频率为200 Hz。采用文献[20]提出的基于定阶消噪的Prony方法识别各工况的模态参数,结果如表 3所示。对比发现,有限元模型和实测无损伤模型的前3阶频率相差较大。文献[21]将该梁的边界条件进行了模型修正,修正效果较好,因此本文不再重复该过程,直接将修正后的模型作为无损伤结构开展损伤识别研究。
| 阶次 | 初始FE模型 | 修正后FE模型 | 物理模型 | ||||
| 无损伤工况 | 损伤工况 | ||||||
| f/Hz | f/Hz | f/Hz | MAC/% | f/Hz | MAC/% | ||
| 1 | 9.060 | 8.018 | 8.018 | 99.985 | 7.93 | 99.88 | |
| 2 | 56.779 | 50.999 | 50.999 | 99.878 | 50.933 | 99.72 | |
| 3 | 159.017 | 143.88 | 143.88 | 99.663 | 143.5 | 99.40 | |
3.2 损伤识别
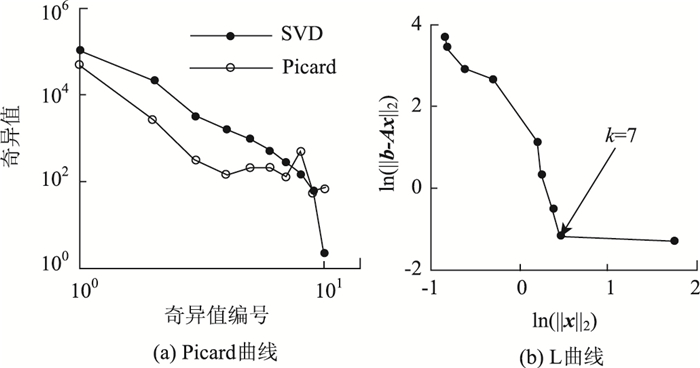
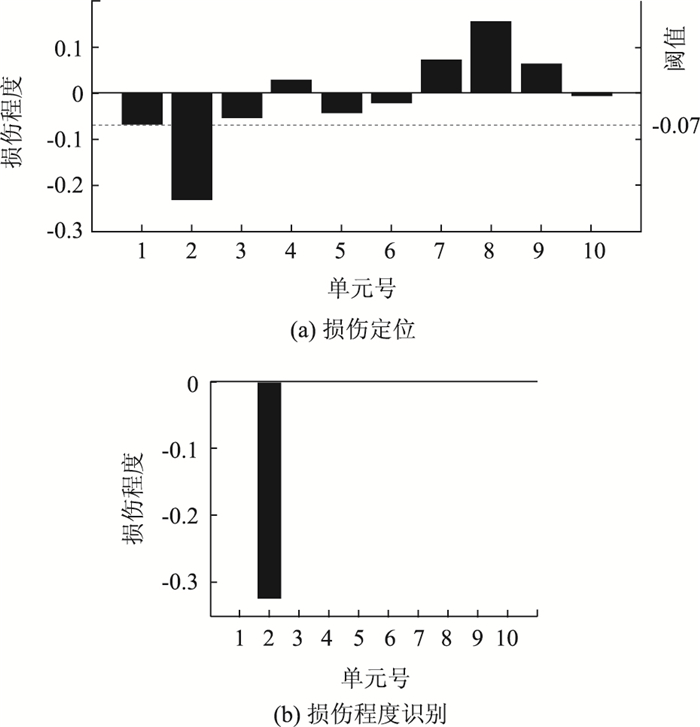
第Ⅰ阶段:首先利用Guyan法将实测的前3阶模态进行扩阶,然后用前3阶实测模态和前10阶有限元模态构建30个CMCM方程。绘出该方程组系数矩阵的Picard曲线和L曲线,如图 13所示。利用TSVD方法进行求解,截断数k=7,结果如图 14(a)所示。结合损伤阈值,可以将损伤定位到单元2。
|
| 图 13 Picard和L曲线(悬臂梁算例) Fig. 13 Picard and L curves (for cantilever beam case) |
| |
|
| 图 14 悬臂梁损伤识别结果 Fig. 14 Damage identification result of cantilever beam |
| |
第Ⅱ阶段:将单元2作为第Ⅱ阶段的损伤识别对象,利用前3阶频率信息采用迭代修正法进行识别,结果如图 14(b)所示,损伤程度为-0.325,与实际损伤程度基本相符。
4 结论基于模型修正的损伤识别方法在桥梁结构的实际应用中仍存在很多问题,本文针对实测模态不完备和测量噪声影响下“病态”方程的求解问题进行了探讨,并分别对一个斜腿刚架桥数值模型和一个悬臂梁物理模型进行了数值和试验研究,结论如下:
(1) CMCM-TSVD方法比传统的CMCM方法具有更强的噪声鲁棒性。该方法不会出现损伤漏判,但随着噪声水平的提高会有虚假损伤出现。
(2) Guyan扩阶和测量噪声均会影响CMCM-TSVD方法对损伤程度的识别精度。
(3) 基于频率的迭代修正法可以有效地避免测量噪声和扩阶误差对损伤识别的影响,但受实测信息量的影响,待识别的单元数不能太多。
(4) 通过探讨优缺点,提出了两阶段损伤识别过程:首先利用Guyan扩阶和CMCM-TSVD方法进行损伤的初步定位,然后利用基于频率的迭代修正法进行损伤的精确识别。数值计算和试验研究表明,利用该两阶段模型修正过程可准确地识别结构损伤。
| [1] | 宗周红, 钟儒勉, 郑沛娟, 等. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J]. 中国公路学报 , 2014, 27 (12) : 46-57 ZONG Zhou-hong, ZHONG Ru-mian, ZHENG Pei-juan, et al. Damage and Safety Prognosis of Bridge Structures Based on Structural Health Monitoring:Progress and Challenges[J]. China Journal of Highway and Transport , 2014, 27 (12) : 46-57 |
| [2] | ALVANDI A, CREMONA C. Assessment of Vibration-based Damage Identification Techniques[J]. Journal of Sound and Vibration , 2006, 292 (1/2) : 179-202 |
| [3] | 杨小森, 闫维明, 陈彦江, 等. 基于振动信号统计特征的损伤识别方法[J]. 公路交通科技 , 2013, 30 (12) : 99-106 YANG Xiao-sen, YAN Wei-ming, CHEN Yan-jiang, et al. Damage Detection Method Based on Statistics Characteristics of Vibration Signal[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (12) : 99-106 |
| [4] | 宋子收, 周奎, 李胡生, 等. 基于曲率模态和小波系数差的损伤识别[J]. 公路交通科技 , 2010, 27 (11) : 61-66 SONG Zi-shou, ZHOU Kui, LI Hu-sheng, et al. Damage Identification Based on Curvature Mode and Difference of Wavelet Coefficients[J]. Journal of Highway and Transportation Research and Development , 2010, 27 (11) : 61-66 |
| [5] | SIMOEN E, ROECK G D, LOMBAERT G, et al. Dealing with Uncertainty in Model Updating for Damage Assessment:A Review[J]. Mechanical Systems and Signal Processing , 2015, 56/57 : 123-149 |
| [6] | WANG S, LI Y, LI H. Structural Model Updating of an Offshore Platform Using the Cross Model Cross Mode Method:An Experiment Study[J]. Ocean Engineering , 2015, 97 : 57-64 |
| [7] | HU S L J, LI H, WANG S. Cross-model Cross-mode Method for Model Updating[J]. Mechanical Systems and Signal Processing , 2007, 21 (4) : 1690-1703 |
| [8] | 李英超.基于模态参数识别的海洋平台结构模型修正技术研究[D].青岛:中国海洋大学, 2012. LI Ying-chao. Study on Finite Element Model Updating for Offshore Platform Structures Based on Modal Parameter Identification[D]. Qingdao:Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012506632.htm |
| [9] | TIKHONOV A N. Solution of Incorrectly Formulated Problems and the Regularization Method[J]. Soviet Mathematics Doklady , 1963 (5) : 1035-1038 |
| [10] | 吴颉尔.正则化方法及其在模型修正中的应用[D].南京:南京航空航天大学, 2007. WU Jie-er. Regularization Method and Its Application in Finite Element Model Updating[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10287-2009053496.htm |
| [11] | 肖庭延, 于慎根, 王彦飞. 反问题的数值解法[M]. 北京: 科学出版社, 2003 . XIAO Ting-yan, YU Shen-gen, WANG Yan-fei. Numerical Solution of Inverse Problem[M]. Beijing: Science Press, 2003 . |
| [12] | 王俊荣.海洋平台结构物损伤检测与模型修正方法研究[D].青岛:中国海洋大学, 2009. WANG Jun-rong. Study on Damage Detection and Model Updating for Offshore Platform Structures[D]. Qingdao:Ocean University of China, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10423-2009160410.htm |
| [13] | WANG S. Iterative Modal Strain Energy Method for Damage Severity Estimation Using Frequency Measurements[J]. Structural Control and Health Monitoring , 2013, 20 (2) : 230-240 |
| [14] | WANG S Q, LI H J. Assessment of Structural Damage Using Natural Frequency Changes[J]. Acta Mechanica Sinica , 2012, 28 (1) : 118-127 |
| [15] | MARES C, FRISWELL M I, MOTTERSHEAD J E. Model Updating Using Robust Estimation[J]. Mechanical Systems & Signal Processing , 2002, 16 (1) : 169-183 |
| [16] | FRISWELL M I, MOTTERSHEAD J E, AHMADIAN H. Finite-element Model Updating Using Experimental Test Data:Paramterization and Regularization[J]. Philosophical Transactions:Mathematical, Physical and Engineering Sciences , 2001, 359 (1778) : 169-186 |
| [17] | 张德文. 模型修正与破损诊断[M]. 北京: 科学出版社, 1999 . ZHANG De-wen. Model Updating and Damage Detection[M]. Beijing: Science Press, 1999 . |
| [18] | 贾俊平, 何晓群, 金勇进. 统计学[M]. 北京: 中国人民大学出版社, 2015 . JIA Jun-ping, HE Xiao-qun, JIN Yong-jin. Statistics[M]. Beijing: China Renmin University Press, 2015 . |
| [19] | WANG S. Model Updating and Parameters Estimation Incorporating Flexible Joints and Boundary Conditions[J]. Inverse Problems in Science and Engineering , 2014, 22 (5) : 727-745 |
| [20] | 包兴先.基于模型定阶和信号消噪的海洋平台结构模态参数识别研究[D].青岛:中国海洋大学, 2010. BAO Xing-xian. Model Order Determination and Noise Removal for Modal Parameter Estimation of Offshore Platform Structures[D]. Qingdao:Ocean University of China, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011030150.htm |
| [21] | 李英超, 张敏, 李华军. 利用不完备实测模态修正杆系结构约束边界条件[J]. 工程力学 , 2013, 30 (1) : 288-294 LI Ying-chao, ZHANG Min, LI Hua-jun. Model Updating for Constraint Boundary Conditions of Member Structures Using Incomplete Measured Modes[J]. Engineering Mechanics , 2013, 30 (1) : 288-294 |
 2016, Vol. 33
2016, Vol. 33
