扩展功能
文章信息
- 贺君, 刘玉擎, 李传习, 张玉平
- HE Jun, LIU Yu-qing, LI Chuan-xi, ZHANG Yu-ping
- 钢-混凝土组合简支梁桥温度影响因素及分布模式
- Temperature Influencing Factors and Distribution Mode of Simply Supported Steel-concrete Composite Girder Bridge
- 公路交通科技, 2016, 33(11): 63-68
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 63-68
- 10.3969/j.issn.1002-0268.2016.11.010
-
文章历史
- 收稿日期: 2016-01-11
2. 同济大学 土木工程学院, 上海 200092
2. School of Civil Engineering, Tongji University, Shanghai 200092, China
桥梁周围大气温度、太阳辐射、风速等环境因素导致结构温度产生时间、空间变化。钢-混凝土组合梁桥,由于日、年温度变化,将产生温度变形、应力以及二次内力,使得适应温度变形的支座与伸缩系统设计较为复杂,尤其对于城市桥梁中广泛采用的钢-混凝土曲线组合梁桥[1]。因此合理的桥梁结构温度荷载模型,成为准确计算结构的温度效应以及有效评估温度作用结构安全性的关键前提。
桥梁温度作用研究开始于20世纪50,60年代,集中于简单结构的一维热传递分析[2]。70,80年代,开始建立二维有限元模型,研究气候条件、截面几何形状、桥梁位置、材料特性等对混凝土箱梁、混凝土-钢组合桥梁时变温度以及截面温度分布的影响[3-4]。Fu[5]建立二维热分析模型对I-型、单箱、双箱截面钢-混凝土组合桥进行参数分析,结果表明桥面板悬臂长度与梁高的比值为截面温度分布的重要影响因素。Tindal [6]提出冬季、夏季简化的温度荷载模型,并通过有限元参数分析研究钢-混凝土组合斜桥温度效应,最终提出相关设计建议。
温度变化引起的应力、变形将影响桥梁结构的力学行为以及耐久性能,得到许多学者的关注[7-8]。Kennedy [7]指出温度应力将导致混凝土桥面开裂,进而引起桥面结构内的钢筋锈蚀,影响其耐久性能。除去温度应力,桥梁设计中必须考虑环境温度引起的桥梁变形。合理预测温度变形至关重要,因为不仅关系桥梁支座以及伸缩装置的设计,而且影响桥梁下部结构墩台的设计[8]。
本文以钢-混凝土组合桥梁为例,建立桥梁截面热传递理论模型,通过有限元热分析得到温度时变曲线,采用验证的有限元模型进行参数分析,研究桥梁曲率、季节、桥面板厚度、悬臂长度以及梁高对截面有效温度、竖向、横向温度梯度的影响;最终,组合箱型截面升温、降温情况下,竖向正、负温差分布模式,并与AASHTO[9],EC[10]等规范规定的温度分布模式进行比较,研究成果可为钢-混凝土组合桥梁温度荷载设计及温度效应评估提供参考。
1 温度场理论 1.1 热传导微分方程桥梁结构温度场通过经典的热传递偏微分方程确定,假定桥梁内部不存在热源,控制方程如下:
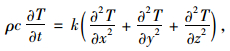
|
(1) |
式中,k为热传导率;c为材料的比热;ρ为材料的密度;T为任意点(x, y, z)的温度;t为时间。对于曲线桥梁,温度分布不仅随时间t变化,而且随不同截面变化。控制方程求解需要提供边界条件与初始条件。
1.2 热边界条件本文考虑第2、3类边界(式2)条件[11]:即边界热通量已知,边界热通量与环境温度同结构表面温度差值成比例关系;对控制方程式(1)进行求解。
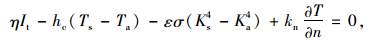
|
(2) |
式中,η为太阳辐射吸收率;It为结构表面太阳辐射总量,计算需考虑太阳与桥梁结构的相对位置,太阳高度角,大气清晰度,风速等条件[4, 5, 12]。hc为桥梁结构表面与周边大气对流系数,与截面几何形状、表面粗糙程度以及风速有关;Ts为桥梁结构表面温度;Ta为大气环境温度,通常通过实测得到;ε为材料发射率;σ为Stefan-Boltzmann常数,取5.67 W/(m2·K4);Ks为桥梁结构表面开氏温度;Ka为大气环境开氏温度;kn为材料热传导系数。
1.3 钢-混凝土界面热接触条件假定钢与混凝土界面处于理想热接触状态[13],即接触界面,钢翼缘板顶面的温度与热流量同与之接触的混凝土板底面的温度与热流量相等,如下:
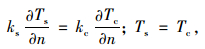
|
(3) |
式中,下标s和c分别为钢与混凝土表面,n为接触面的法向方向。
1.4 初始条件由于实测温度传感器布置有限,通常难以得到桥梁结构截面完全精确的温度分布。因此,可以通过假定截面温度为初始时刻环境温度,且均匀分布,同时施加实测的环境温度以及太阳辐射量作为边界条件进行初步计算,得到非均匀分布的截面温度为初始条件[14]。
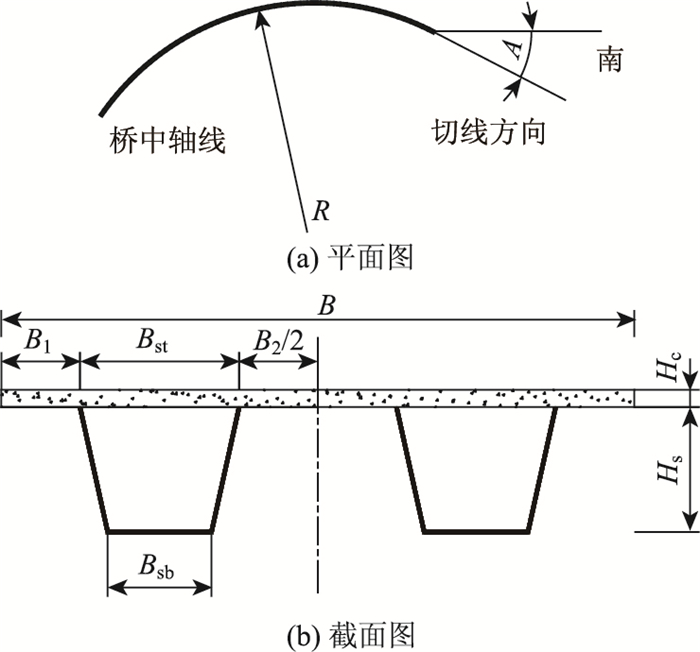
2 研究对象及有限元分析 2.1 研究对象桥以一座跨径为40 m的钢箱梁-混凝土桥面板组合简支梁桥为例,研究钢-混凝土组合箱梁的温度分布模式。该桥中轴线的曲率半径R为420 m。组合截面梁高(Hs+Hc)为1.65 m,桥面宽B为7.2 m,混凝土桥面厚度Hc为0.2 m, 悬臂板宽度B1为0.9 m,钢箱梁顶、底宽度Bst, Bsb分别为1.8,1.2 m,两钢箱梁间距B2为1.8 m。桥面采用水泥混凝土铺装,桥梁整体布置如图 1所示。跨中截面,混凝土桥面与钢腹板、底面布置温度传感器测试组合截面的温度分布。
|
| 图 1 桥梁布置 Fig. 1 Bridge layout |
| |
2.2 有限元模型
本文采用通用有限元软件ANSYS[15]进行热传导微分方程求解。建立整个桥梁的三维模型进行热传递分析,研究复杂环境条件下桥梁温度分布模式。为了进行比较,同时建立二维截面简化模型。由于钢腹板与底板厚度较小,假定温度沿厚度方向为常数。3D模型中,混凝土桥面板,钢腹板与底板分别采用实体单元Solid 90与板壳单元Shell132模拟;2D模型中,采用平板单元plane 77模拟;通过边界表面单元Surf 152 (3D)和Surf 151 (2D)施加热传递边界条件,如图 2所示的实测温度、太阳辐射量。
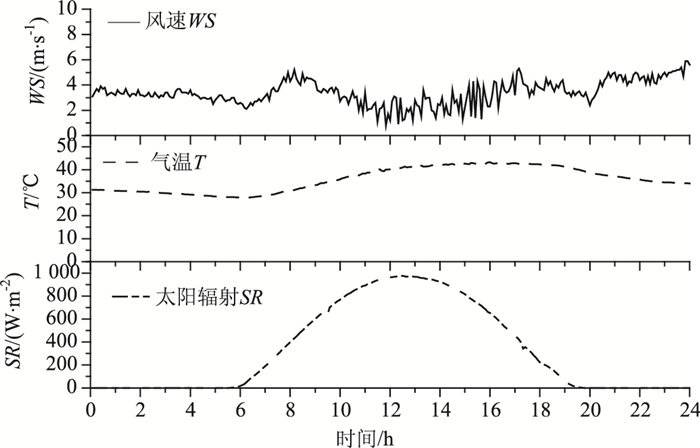
|
| 图 2 2012-8-1桥址附近风速、气温、太阳辐射实测数据 Fig. 2 Wind speed, ambient temperature and solar radiation near bridge on Aug. 1, 2012 |
| |
通常混凝土桥面板的厚度为15~30 cm,温度梯度沿厚度方向变化明显,合理划分模型单元为准确获得温度模式的关键因素之一。通过单元网格敏感性分析得到混凝土厚度方向多于4层单元,且纵向桥单元长宽比小于5,能较好得到非线性温度梯度。热传导瞬态分析结果准确程度与时间步长相关,时间步长太大可能丢失重要峰值信息,时间步长太小计算时间大幅增加。数值计算表明时间步长为1 h,能够得到满意的结果。
极端气象条件,包括强太阳辐射、环境高温,以及低风速,将产生截面较大温差。本文选取距离桥址位置3 km处气象站点,2012年8月1日的环境温度、太阳辐射以及风速作为热传递环境参数(图 2),代入式(2)计算边界条件,输入3D和2D有限元模型。钢与混凝土材料的热力学特性分别为:钢热传导系数取46 W/(m·℃);热容取486 J/(kg·℃);热吸收与辐射率分别取0.7与0.9。混凝土热传导系数取1.5 W/(m·℃);热容取960 J/(kg·℃);热吸收与辐射率分别取0.6与0.8。
2.3 有限元分析结果(1) 温度时变历程
通过有限元热传导分析,得到截面不同位置温度随时间变化趋势。图 3为2012年8月1日,混凝土板顶面与钢梁底面实测温度时变曲线同三维与二维有限元计算结果比较。混凝土板顶面温度达到最高(46 ℃)发生在下午14:00左右,而钢梁底面最高温度(42 ℃)发生在17:30左右。
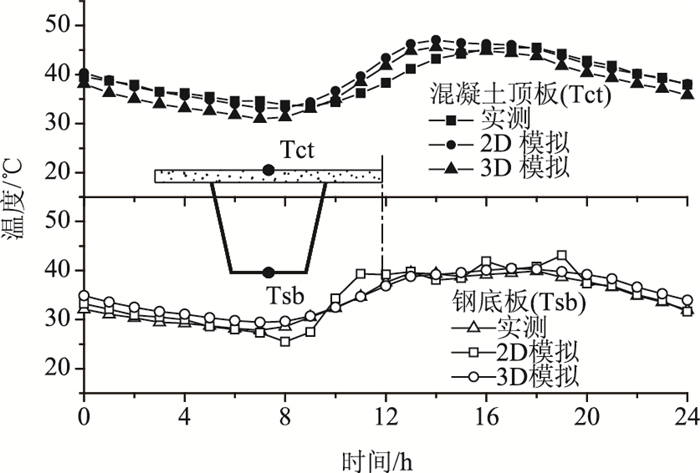
|
| 图 3 截面温度时程曲线实测与模拟比较 Fig. 3 Comparison of sectional temperature curves between simulation and measurement |
| |
三维与二维模型均能较好地体现温度随时间的变化规律,三维模型更好地与实测结果吻合。当桥梁截面沿纵向一致,由于纵向热传递量很小,二维模型能够满足精度要求。
(2) 截面温度分布
桥梁截面实测温度分布同三维有限元计算结果比较如图 4所示,仅以清晨6:00与下午14:00的比较结果为例。清晨6:00截面温度分布均匀,大致与环境温度相等,可以选择为计算初始时刻。下午16:00,混凝土桥面板出现明显的温度梯度,而钢梁沿高度方向温度变化不大。同样,三维有限元模型截面温度分布与实测结果基本吻合,有效验证有限元模型与参数的合理性。
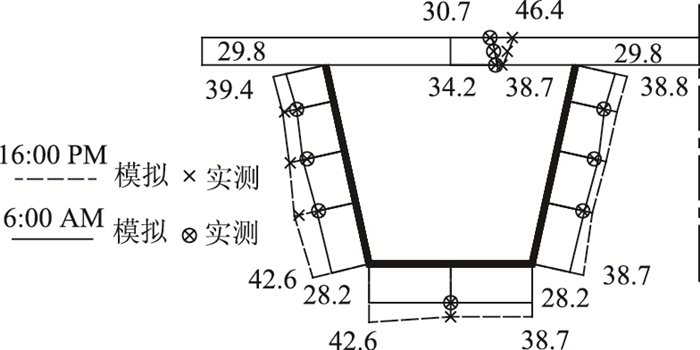
|
| 图 4 截面温度分布实测与模拟比较(单位:℃) Fig. 4 Comparison of sectional temperature distributions between simulation and measurement (unit:℃) |
| |
3 参数分析
钢-混凝土组合桥梁的温度分布受地理位置、环境条件、材料参数以及桥梁布置等因素影响,本文采用上节验证的有限元模型进行定量的参数分析,研究桥梁曲率R、季节、桥面板厚度Hc、钢梁高度Hs;桥面板悬臂长度B1对截面有效温度Teff与梯度温度Tvd, Thd的影响。
桥梁截面温度随时间和位置变化,但截面的平均温度Teff通常用来控制桥梁的纵向位移,见式(4):
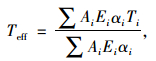
|
(4) |
式中i为截面沿竖向的分层;Ai, Ei, αi, Ti分别为第i层的面积、弹性模量、热膨胀系数、温度。
桥梁截面温度分布通常较为复杂,沿竖向和横向呈现非线性分布,将产生不均匀变形,如果受到约束,导致额外的附加应力,对结构的安全及耐久性带来隐患,因此桥梁的温度梯度,尤其沿高度方向的竖向温度梯度得到了广泛的研究。为简化分析,便于比较不同参数对温度分布的影响,本文定义竖向Tvd与横向Thd温差,见式(5)、(6):
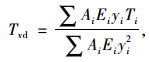
|
(5) |
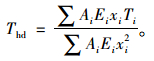
|
(6) |
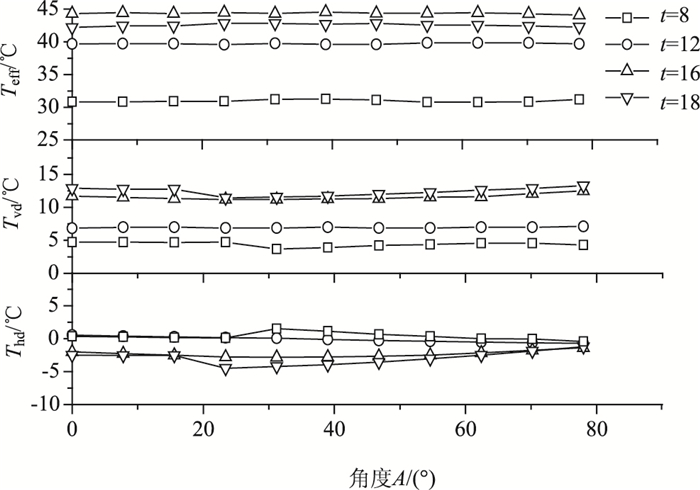
曲线桥梁沿桥轴方向,不同截面太阳辐射角度不一致,因此可能产生纵向的温度梯度。为评价曲率对温度的影响,将研究对象桥曲率半径减小至120 m,桥长与截面尺寸不变,以最不利的夏季环境输入有限元模型进行热传递分析,得到沿桥长方向不同截面Teff,Tvd,Thd,如图 5所示。结果表明:曲率对截面有效温度几乎不影响,可以忽略;曲率对竖向梯度温差影响较小,仅在钢腹板受到太阳直射的时刻(t=8, 18)。曲率对横向度温差影响明显,当一侧钢腹板受到太阳直射(t=8),钢腹板迅速升温,产生较大正温差,当t=18,另一侧钢腹板直射,产生较大负温差。由于曲率仅对横向温度梯度影响明显,通过限制桥梁曲率减小横向温差。
|
| 图 5 曲率影响 Fig. 5 Effect of curvature |
| |
3.2 季节影响
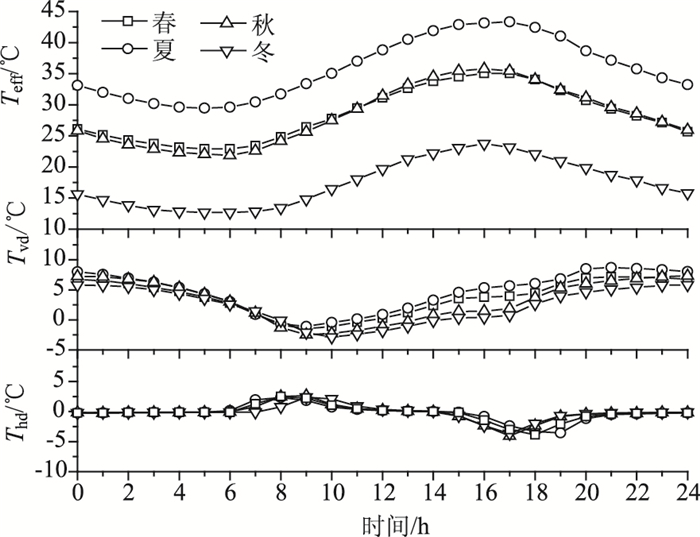
环境条件依季节而变,本文选取春、夏、秋、冬四季中各一天的温度、太阳辐射以及风速作为热传递边界条件输入分析模型,得到不同季节截面Teff,Tvd,Thd,如图 6所示。季节对截面有效温度影响明显,夏季气温高,太阳辐射强,截面有效温度最高,相反冬季气温低,太阳辐射弱,截面有效温度最低。同样,季节对截面竖向温差影响显著,最大竖向正、负温差分别出现在夏季与冬季,由于太阳辐射为温度梯度的主要影响因素,且最大竖向正温差出现在日落以后,因为钢梁降温比混凝土板迅速。季节对截面横向温差绝对值几乎没有影响,仅影响最大温差出现的时刻(日出、日落时刻左右),由于不同季节日出、日落时间不同。
|
| 图 6 季节影响 Fig. 6 Effect of seasons |
| |
3.3 桥面板悬臂长度影响
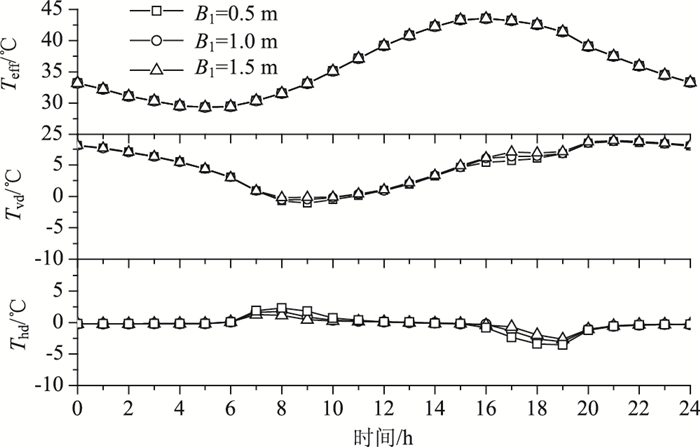
桥面板悬臂长度影响钢腹板太阳直射的区域。选取不同悬臂板长度(B1=1, 1.5, 2 m),研究悬臂长度对截面温度分布影响。钢梁几何尺寸保持不变,夏季天气条件作为环境输入参数。得到不同桥面悬臂长度Teff,Tvd,Thd,如图 7所示。桥面板悬臂长度几乎不影响截面有效温度。悬臂长度对截面竖向温差影响仅发生在腹板太阳直射时间(8:00-10:00;16:00-18:00),悬臂板越短,腹板阴影区域越小,接受太阳辐射越多,因此竖向温差越小。同样,悬臂长度对截面横向温差影响在日出、日落时刻附近显著,悬臂板越短,腹板太阳辐射越大,横向温差越明显。
|
| 图 7 桥面板悬臂长度影响 Fig. 7 Effect of deck overhang length |
| |
3.4 桥面板厚度影响
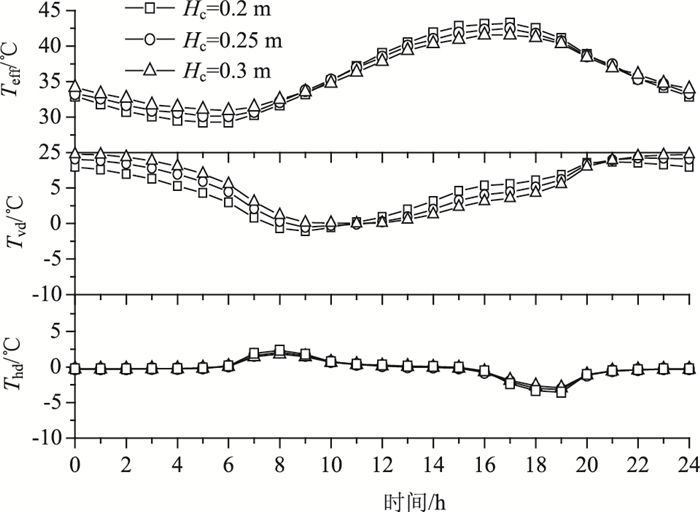
桥面板选取不同厚度(Hc=0.2, 0.25, 0.3 m)的混凝土板,研究其厚度对组合截面温度分布的影响。钢梁几何尺寸保持不变,夏季天气条件作为环境输入参数。得到不同桥面板厚度Teff,Tvd,Thd,如图 8所示。桥面板厚度对截面有效温度有一定影响。因为混凝土表面吸收太阳辐射,当桥面板厚度增加,表面区域与整个桥面板体积的比例减小,加权有效温度降低。桥面板厚度对截面竖向温差影响显著,随着桥面板厚度增加,竖向正温差增加,而负温差减小。同样,桥面板厚度影响截面横向温差,但程度小于竖向温差,随桥面板厚度增加,横向正、负温差均略有减小。
|
| 图 8 桥面板厚度影响 Fig. 8 Effect of deck thickness |
| |
3.5 钢梁高度影响
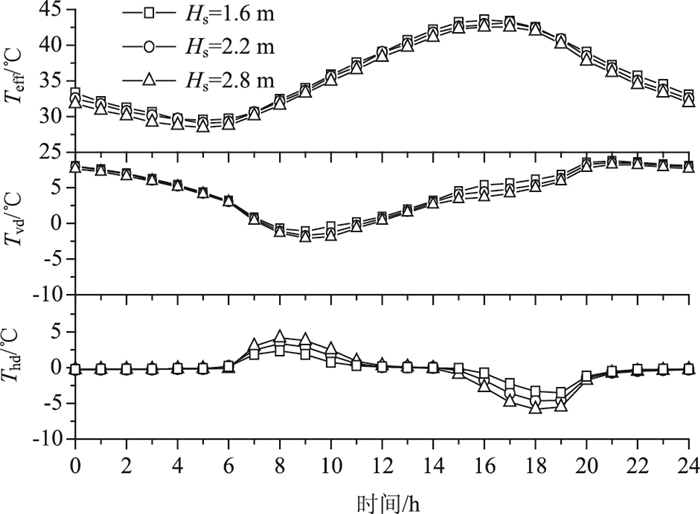
不同钢梁高度直接影响钢腹板太阳辐射的区域,选取不同高度钢梁(Hs=1.6, 2.2, 2.8 m),研究其对组合截面温度分布的影响。混凝土桥面板几何尺寸保持与对象桥不变,夏季天气条件作为环境输入参数。得到不同钢梁高度Teff,Tvd,Thd,如图 9所示。钢梁高度对截面有效温度几乎不影响。钢梁高度对截面竖向温差影响仅发生在腹板太阳直射时间(8:00-12:00; 14:00-18:00),钢梁高度越大,腹板阴影区域越小,接受太阳辐射越多,因此竖向温差越小。同样,钢梁高度对截面横向温差影响在日出、日落时刻附近显著,钢梁高度越大,腹板太阳辐射面积越大,横向温差越明显。
|
| 图 9 钢梁高度影响 Fig. 9 Effect of height of steel girder |
| |
4 温度分布模式
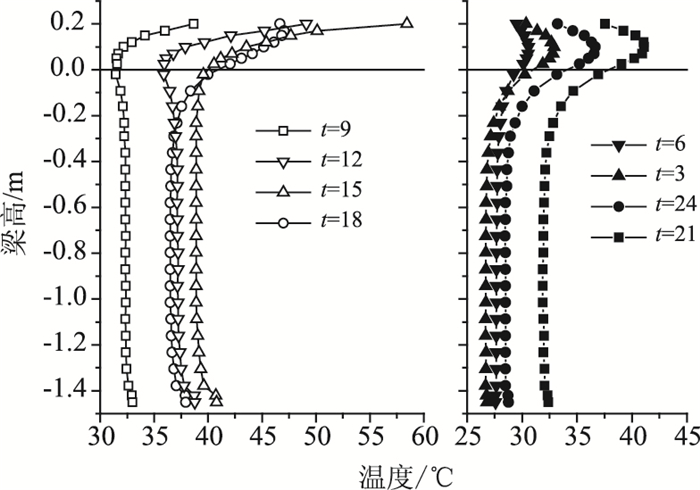
钢-混凝土组合截面横向、竖向温度分布为确定温度梯度荷载的主要因素。为简化分析,横向温度梯度按欧洲规范(2003)[10]规定取线性分布。竖向温度梯度依据有限元分析结果,取截面宽度方向平均温度沿高度方向的分布,如图 10所示,其中x轴(y=0)取钢-混凝土界面。截面竖向温度分布随时间变化,日出之前(7:00),温度分布较为均匀,最大竖向正、负温差分布出现在下午15:00和凌晨1:00。
|
| 图 10 竖向温度分布 Fig. 10 Vertical temperature distribution |
| |
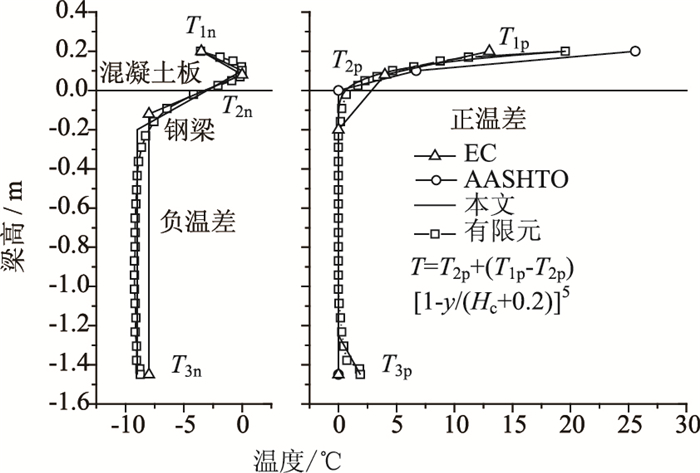
依据有限元分析结果,提出升温与降温情况下,竖向正、负温差分布模式,如图 11所示。
|
| 图 11 竖向温度梯度模式比较 Fig. 11 Comparison of vertical temperature gradient mode |
| |
T1n, T2n, T3n, 分别为降温情况下混凝土顶板最低温度、混凝土板中部温度、钢梁底板平均温度。
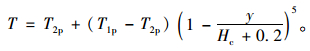
|
(7) |
式中,T1p, T2p, T3p,分别为升温情况下混凝土顶板最高温度、钢腹板中部平均温度、钢梁底板平均温度;由于太阳辐射受到地面反射,通常T3p稍大于T2p。Hc为混凝土板的厚度。
将提出的温度模式与AASHTO,EC规范进行比较,结果表明,正温度梯度,AASHTO规范偏于保守,而EC规范偏于危险;负温度梯度,EC规范温差值小于有限元模拟值,偏不安全,AASHTO未明确给出负温度梯度,本文提出的温度梯度同有限元模拟值吻合较好,可供参考。
本文提出的温度分布模式基于研究对象桥(简支组合箱梁桥)当地的气象数据,且桥面为水泥混凝土铺装,对于地域、桥梁结构体系、截面形式以及桥面铺装类型(如沥青材料)等因素对温度模式的影响有待进一步研究,逐步完善组合桥梁温度荷载模型。
5 结论(1) 组合截面有效温度对桥梁曲率不敏感,竖向和横向温差受桥梁曲率影响,尤其在日出、日落附近时刻。
(2) 组合截面最大有效温度出现在夏季高温与太阳辐射强的晴天,相反最小有效温度出现在冬季低温与太阳辐射弱的阴天。
(3) 混凝土板厚度越小,截面有效温度越高,横向温差越大,由于实际桥面厚度仅为15~30 cm,混凝土桥面板厚度影响相对有限;
(4) 混凝土桥面板悬臂长度以及钢梁的高度对组合截面的横向温度梯度影响显著,悬臂长度与钢梁高度之比越小,横向温差越大。悬臂长度与钢梁高度对截面有效温度及竖向温差的影响可以忽略。
(5) 横向温度梯度仅在日出、日落附近时刻,腹板受到太阳直射的情况下需要考虑,其他时刻可以忽略。混凝土板沿宽度方向分布相对均匀,因此,可以采用有效温度、线性横向温差以及非线性竖向温差对截面温度分布进行描述。
(6) 提出适用本桥的钢-混凝土组合截面升温、降温情况下,竖向正、负温差分布模式,并与AASHTO,EC等规范规定模式进行比较,提出的温度梯度模式需要通过更多的组合结构桥梁(考虑地域、桥梁截面形式等综合因素)的数值模拟与实测结果进行验证。
| [1] | 刘玉擎. 组合结构桥梁[M]. 北京: 人民交通出版社, 2005 . LIU Yu-qing. Steel-concrete Hybrid Bridge[M]. Beijing: China Communications Press, 2005 . |
| [2] | ZUK W. Thermal Behavior of Composite Bridges Insulated and Uninsulated Highway Research Record 76[R]. Washington, D.C.:National Research Council, 1965:231-253. |
| [3] | PRIESTLEY M J. Thermal Gradients in Bridges:Some Design Considerations[J]. New Zealand Engineering , 1972, 27 (7) : 228-233 |
| [4] | ELBADRY M M, GHALI A. Temperature Variations in Concrete Bridges[J]. Journal of Structural Engineering , 1983, 109 (10) : 2355-2374 |
| [5] | FU H C, NG S F, CHEUNG M S. Thermal Behavior of Composite Bridges[J]. Journal of Structural Engineering , 1990, 116 (12) : 3302-3323 |
| [6] | TINDAL T T, YOO C H. Thermal Effects on Skewed Steel Highway Bridges and Bearing Orientation[J]. Journal of Bridge Engineering , 2003, 8 (8) : 57-65 |
| [7] | KENNEDY J, SOLIMAN M. Temperature Distribution in Composite Bridges[J]. Journal of Structural Engineering , 1987, 113 (3) : 475-482 |
| [8] | ROEDER C W. Proposed Design Method for Thermal Bridge Movements[J]. Journal of Bridge Engineering , 2003, 8 (1) : 12-19 |
| [9] | AASHTO. AASHTO LRFD Bridge Design specifications:6th ed.[S]. Washington, D.C.:American Association of State Highway and Transportation Officials. 2012. |
| [10] | EUROCODE 1, Actions on Structures, Part 1-5:General Actions-Thermal Actions[S]. |
| [11] | NODA N, HETNARSKI R B, TANIGAWA Y. Thermal Stresses[M].2nd ed. New York: Taylor & Francis, 2003 . |
| [12] | THRELKELD J L. Thermal Environmental Engineering[M]. Englewood Cliff, NJ: Prentice-Hall Inc, 1970 . |
| [13] | TONG M, THAM L G, AU F T K, et al. Numerical Modelling for Temperature Distribution in Steel Bridges[J]. Computers and Structures , 2001, 79 (6) : 583-593 |
| [14] | KONG B, CAI C S, KONG X. Thermal Behaviors of Concrete and Steel Bridges after Slab Replacements with GFRP Honeycomb Sandwich Panels[J]. Engineering Structure , 2013, 56 : 2041-2051 |
| [15] | ANSYS Inc. ANSYS Theory Manual for Version 15.0[M]. Pittsburgh, US: Swanson Analysis Systems, Inc., 2013 . |
 2016, Vol. 33
2016, Vol. 33
