扩展功能
文章信息
- 刘丽芬, 武贤慧
- LIU Li-fen, WU Xian-hui
- 基于改进层次分析法的城市道路横断面评价方法
- An Evaluation Method of Urban Road Cross-section Based on Improved AHP
- 公路交通科技, 2016, 33(11): 50-56
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 50-56
- 10.3969/j.issn.1002-0268.2016.11.008
-
文章历史
- 收稿日期: 2016-06-20
2. 西安市政设计研究院有限公司, 陕西 西安 710068;
3. 长安大学建工学院, 陕西 西安 710064
2. Xi'an Municipal Engineering Design & Research Institute Co., Ltd., Xi'an Shaanxi 710068, China;
3. School of Civil Engineering, Chang'an University, Xi'an Shaanxi 710064, China
道路横断面是城市道路设计中的一项核心内容,它直接影响道路的使用功能和节能环保,决定了一条道路的整体景观,并影响一个城市的建设特色和品位,也是设计师设计理念、风格、品味的重要展示。
近几年,随着城市建设的快速发展,城市化水平的不断提高,机动车保有量呈井喷式增长,城市建设与土地供给矛盾日益突显,城市道路建设者和设计师需要破解两大难题:一是空间资源最大有效化利用问题,二是如何科学合理地解决人、车、路之间的矛盾问题[1]。城市道路横断面设计的评价涉及到大量指标,包括交通规划与管理领域的复杂模型数据和道路设计施工的工程设计参数[2-3], 且各个区域都有其道路发展的脉络和历史沿革,这就为评价掺杂了许多人为因素和偶然因素。因此城市道路横断面的选型更需要一个客观的、科学的工程评价体系支撑。
目前在横断面方案的评价方法上,还存在许多主观判断和模糊概念。在模糊综合评价方法中,体现评价体系是否科学有效的一项工作就是权重矩阵的构建,在工程建设领域主要利用专家打分法等主观性方法构建权重矩阵[4-5]。一般在公路、铁路等外部资料较难获取的情况下,专家打分法较为准确。但市政道路横断面承载着交通功能、景观功能、空间需求、市政设施布置以及防灾减灾等诸多要求,专家打分法不是很客观。因此,层次分析法或模糊重构EDA模型等评价方法开始应用[6-8]。层次分析法(AHP)是从定性分析到定量分析综合集成的一种典型的系统工程方法,其在实用中存在的主要问题是如何构造、检验和修正判断矩阵的一致性问题和计算判断矩阵各要素的权重。目前已提出的处理方法的主要问题是主观性强、修正标准对原判断矩阵而言不能保证是最优的或只对判断矩阵的个别元素进行修正,但至今尚没有一个统一的修正模式,实际应用AHP时多数是凭经验和技巧进行修正,缺乏相应的科学理论和方法指导。如何针对横断面复杂的影响因素,对层次分析法进行改进, 使其更具客观性,还需进一步深入研究。基于此,本文分析了城市道路横断面设计的影响因素,构建了包括交通需求、道路设计、环境及人性化要求子项目在内的横断面设计评价指标体系,基于模糊数学隶属度的理论,采用改进的层次分析法建立了城市道路横断面方案的模糊综合评判模型。
1 城市道路横断面设计影响因素分析 1.1 传统横断面设计横断面各组成部分的宽度以及车道数主要是根据设计小时交通量来确定,并选择合理的交通组织及横断面布置方案[9]。设计小时交通量根据预测的远景交通量以及本道路的设计服务水平等来确定,如图 1所示。
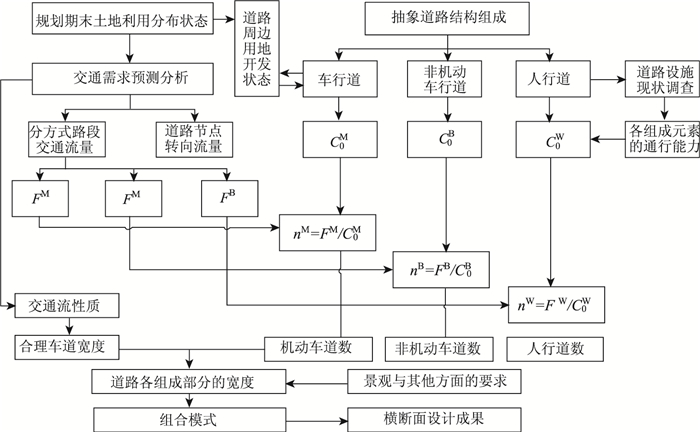
|
| 图 1 道路横断面设计基本流程 Fig. 1 Flowchart of designing road cross-section |
| |
我国《城市道路工程设计规范》(CJJ37-2012)将横断面分为以下5种形式:单幅路、两幅路、三幅路、四幅路以及特殊形式的横断面,各种横断面分别适用于不同的交通需求特征和道路空间特征[10]。
道路横断面作为道路各项功能发挥的载体,在设计时应为各功能提供充足的空间[11],即横断面的各组成部分分配空间应合理。但由于道路的功能不同,各功能部分所需要的空间大小也不同,如何合理地分配各部分所需要的空间,是道路横断面设计的关键。道路横断面空间功能主要包括主体功能、附属功能、其他功能等,如图 2所示。这些功能需求对横断面设计产生了重要影响。
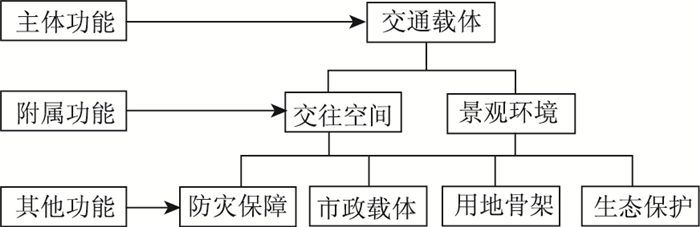
|
| 图 2 城市道路功能 Fig. 2 Urban road functions |
| |
1.2 交通功能对道路横断面设计的影响分析
城市道路系统规划应满足城市客、货运车流和人流的安全与畅通。城市道路横断面交通功能主要通过空间划分和交通组织方式体现,主要包括:设计速度、道路通行能力、路权划分,特别是机动车道宽度、非机动车道宽度及人行道宽度的合理划分,交叉口进口道横断面空间划分、交叉口形式的布置,人行过街方式的选择,各种交通隔离措施的应用等。
1.3 空间及景观功能对道路横断面设计的影响分析附属功能主要包括交往空间及景观环境, 主要体现在人文功能及景观功能两方面。通过无障碍设施的安全性和连续性、沿线单位出入口的行人组织、公交专用道及港湾式公交站的设置,人行过街设施的设置等,体现出以人为本的人文设计理念;道路横断面是景观功能的集成与体现,横断面各部分尺寸、比例及协调性,绿化形式及绿化效果、道路铺装的整体效果、外露构筑物的选型、材料及装饰等都对城市道路的景观起到了重要影响。
1.4 其他功能对道路横断面设计的影响分析道路的其他功能包括市政载体、防灾保障、用地骨架及生态保护。在道路红线宽度内,包括了地下设计管线、照明、电力、交通管理设施等公用设施,横断面设计中应考虑管线及各种公共设施布设的科学性和合理性;地下道路应合理设置逃生通道及防火设施;横断面宽度及形式应与两侧土地性质相匹配;横断面设计应对现状植被及行道树进行合理生态保护。
2 城市道路横断面方案评价指标体系构建在影响横断面设计的诸多因素中,交通需求、道路空间设计、环境和人性化要求是主导因素,本文将这些因素作为评价指标。
2.1 交通需求因素交通需求因素主要从市政道路的交通功能实现方面进行指标的选取,其中包括对方案中可能产生的交通量、机动车和非机动车通行过程中互相可能产生的影响、车辆在运行时产生的延误等交通运营特征的指标选取,以及设计断面的通行能力等方面。
2.2 道路空间设计因素道路空间设计因素主要从市政道路横断面设计中具体的断面布局来进行指标选取,包括横断面的红线宽度、绿化带宽度、车道数的选取、车道宽度的设计、是否有渠化设计、公交站台的设计以及造价等因素。道路设计指标的选取充分考虑了在市政道路横断面设计中决定横断面形式的各类设计指标。
2.3 环境和人性化因素道路的使用是以人为主体,所以设计中需要充分考虑行人、驾驶员等道路使用者的行为习惯。同时,道路作为城市不可分割的一部分,也对城市景观和人居环境产生一定影响。环境和人性化因素,主要从道路使用者的角度和对环境影响程度出发,以行人过街、非机动车道宽度、二次过街长度作为行人和非机动车通行条件指标,以公交专用道宽度作为公共交通通行条件指标,以地下管线的设置等因素作为对城市现状地下工程的影响指标。
综上所述,构建了城市道路横断面评价指标体系,见图 3。
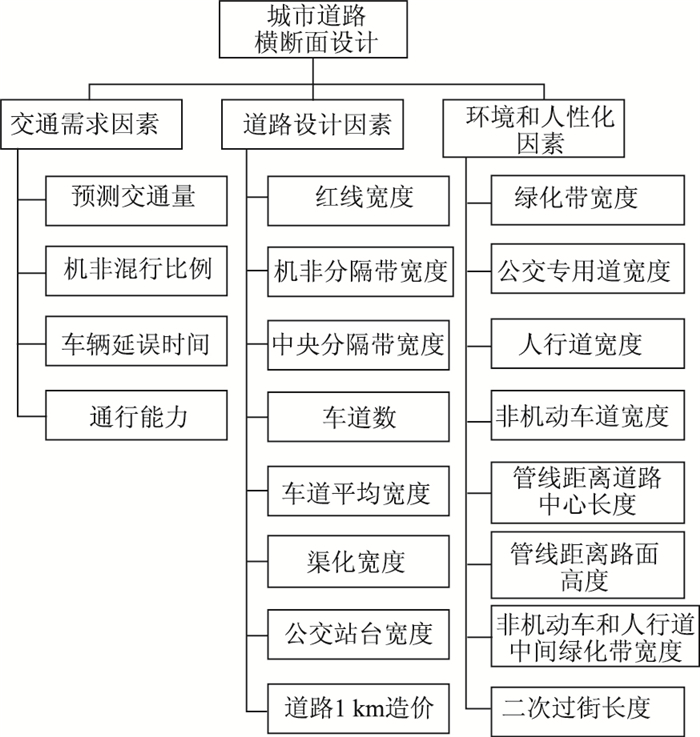
|
| 图 3 横断面评价指标体系 Fig. 3 Evaluation index system of road cross-section |
| |
3 改进的层次分析法基本原理及分析方法 3.1 基本原理
层次分析法是系统工程中对非定量事件做出定性与定量相结合的一种系统分析方法, 特别适用于处理多目标、多层次的复杂大系统问题[12]。在一般评价中, 对于一些无法测量的因素, 只要引入合理的标度, 就可以用这种方法来度量各因素的相对重要性, 从而为决策提供依据。层次分析法中判断矩阵的一致性问题一直是一个难点, 虽然在实际应用中, 可以凭借大致的估计来调整判断矩阵, 但这样毕竟带有主观性和盲目性, 并且调整的过程相当复杂, 往往需多次重新赋值[13]。为此, 本文引入最优传递矩阵, 对AHP法进行改进:不采用传统的专家打分法进行方案评价,而是利用相对隶属度矩阵构建一个权重判断矩阵对方案进行评价。这样在评价开始阶段就满足一致性要求, 直接求出权重值, 避免了后期的一致性检验。
3.2 评价模型 3.2.1 由各评价指标建立各指标的相对隶属度矩阵隶属度属于模糊评价函数中的概念,模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法,其特点是评价结果不是绝对的肯定或否定,而是以一个模糊集合来表示。相对隶属度是设立参考系的隶属度。
根据所研究评价系统的实际情况, 从代表性、系统性和适用性等的角度, 建立模糊综合评价的评价指标体系, 由各评价指标的样本数据建立单评价指标的相对隶属度的模糊评价矩阵[14]。为了尽可能保持各评价指标值的变化信息,对越大越优型指标的标准化处理公式可取为:
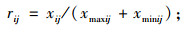
|
(1) |
越小越优型为:
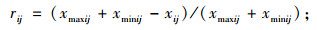
|
(2) |
越中越优型为:
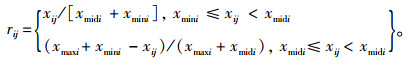
|
(3) |
上述式中:xij为指标值,xmaxij,xminij分别为方案集中第i行的最大值、最小值;rij为标准化后的评价指标值。
从而可得模糊评价矩阵为:
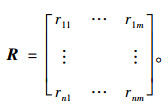
|
(4) |
根据模糊评价矩阵R=(r(i, j))n×m构造用于确定各评价指标权重的判断矩阵B=(bij)n×n。模糊综合评价的实质是一种优选过程, 从综合评价角度看, 若评价指标i1的样本系列{r(i1, j)|j=1~m}与区域统计值和模型预测值的变化程度大于其他方案, 则评价指标i1传递的综合评价信息比其他方案传递的综合评价信息多。基于此, 可用各评价指标与区域均值和模型预测值之间的差值的样本标准差s(i)来反映各评价指标对综合评价的影响程度, 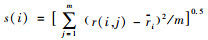
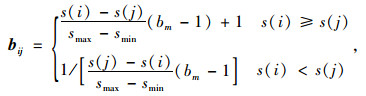
|
(5) |
式中,smin,smax分别为{s(i)|i=1~n}的最小值和最大值; 相对重要性程度参数值bm=min{19, int[smax/smin+0.5]}=19, min和int分别为取小函数和取整函数。
采用规范平均法来计算矩阵的权重向量W。将判断矩阵B的各个列向量先归一化,再平均,得到W的近似解进行一致性检验。
(3) 综合评价值的确定
综合评价值Fq=Rq·WT,R为模糊评价矩阵,W为权重向量,把各评价指标的权重值wi与各方案相应评价指标的相对隶属度值r(i, j)相乘并累加, 可得模糊评价的综合指标值z(j)[15]。
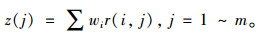
|
(6) |
综合指标值z(j)越大说明第j个方案越优, 据此可进行科学决策。
4 工程实例分析某一市政道路,红线宽度为40 m,横断面设计提出了3个方案,具体参数如表 1所示。
| 序号 | 评价指标 | 横断面方案1 | 横断面方案2 | 横断面方案3 | 区域统计值和模型预测值 | ||||||
| 评价指标值 | 相对隶属度 | 评价指标值 | 相对隶属度 | 评价指标值 | 相对隶属度 | ||||||
| 1 | 红线宽度/m | 40 | 1 | 40 | 1 | 40 | 1 | - | |||
| 2 | 预测交通量/(veh·h-1) | 4 105 | 0.497 | 4 200 | 0.485 | 3 958 | 0.491 | 4 101 | |||
| 3 | 机非混行比例/% | 0.12 | 0.556 | 0.14 | 0.481 | 0.15 | 0.444 | - | |||
| 4 | 车辆延误时间/s | 21 | 0.571 | 24 | 0.510 | 28 | 0.429 | - | |||
| 5 | 通行能力/(veh·h-1) | 5 410 | 0.505 | 5 310 | 0.495 | 5 104 | 0.476 | - | |||
| 6 | 公交专用道宽度/m | 3.5 | 1.000 | 3.5 | 1.000 | 0 | 0.000 | - | |||
| 7 | 非机动车道宽度/m | 3.5 | 0.583 | 3 | 0.500 | 2.5 | 0.417 | - | |||
| 8 | 非机动车和人行道中间绿化带宽度/m | 1.5 | 1.000 | 0 | 0.000 | 0 | 0.000 | - | |||
| 9 | 机非分隔带宽度/m | 2 | 0.571 | 1.5 | 0.429 | 0 | 0.000 | - | |||
| 10 | 中央分隔带宽度/m | 2.5 | 0.833 | 1 | 0.333 | 0.5 | 0.500 | - | |||
| 11 | 双向车道数 | 6 | 0.500 | 6 | 0.500 | 6 | 0.500 | - | |||
| 12 | 车道平均宽度/m | 3.5 | 0.517 | 3.75 | 0.483 | 3.25 | 0.481 | 3.5 | |||
| 13 | 单侧渠化宽度/m | 25 | 0.714 | 15 | 0.429 | 10 | 0.286 | - | |||
| 14 | 绿化率/% | 35 | 0.583 | 25 | 0.417 | 30 | 0.500 | - | |||
| 15 | 人行道宽度/m | 4 | 0.667 | 2 | 0.333 | 3 | 0.500 | - | |||
| 16 | 横坡度/% | 1.5 | 0.625 | 2.5 | 0.375 | 2 | 0.571 | 1.5 | |||
| 17 | 公交港湾宽度/m | 3 | 0.625 | 5 | 0.375 | 0 | 0.000 | 3 | |||
| 18 | 管线距离道路中心长度/m | 15 | 0.571 | 8 | 0.304 | 20 | 0.429 | 15 | |||
| 19 | 道路1 km造价/万元 | 3 250 | 0.495 | 3 450 | 0.518 | 3 850 | 0.462 | 3 310 | |||
| 注:相对隶属度公式见公式(1)、(2)、(3)。 | |||||||||||
该方案评价指标集中,序号11,13,14,15为越大越优型指标,序号3,4为越小越优型指标,2,12,16,17,18,19为越中越优型指标。
横断面模糊评价矩阵为R=
采用规范平均法来计算矩阵的权重向量W。将判断矩阵的各个列向量先归一化,再平均,得到W的近似解进行一致性检验。
W=(0.006 0.012 0.014 0.007 0.261 0.016 0.261 0.083 0.065 0.006 0.008 0.052 0.016 0.036 0.027 0.092 0.027 0.008)。
BW=(0.011 0.013 0.014 0.011 0.325 0.014 0.325 0.052 0.038 0.011 0.011 0.030 0.014 0.022 0.018 0.060 0.018 0.012)T。
最大特征根为:λm=19.875。
计算一致性指标,为
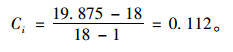
|
又当n=18时,随机性指标Ri为1.613 3,则相对一致性指标:
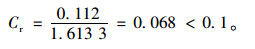
|
因此,一致性可以接受,即B是相容的, 故可用W作为权重向量。
在横断面评价中,本次设计共3个方案(m=3),得到3个方案的评价值,见表 2。
| 方案1 | 方案2 | 方案3 | |
| 预测交通量/(veh·h-1) | 0.003 | 0.003 | 0.003 |
| 机非混行比例/% | 0.007 | 0.006 | 0.005 |
| 车辆延误时间/s | 0.008 | 0.007 | 0.006 |
| 通行能力/(veh·h-1) | 0.004 | 0.004 | 0.003 |
| 公交专用道宽度/m | 0.261 | 0.261 | 0.000 |
| 非机动车道宽度/m | 0.010 | 0.008 | 0.007 |
| 非机动车和人行道中间绿化带宽度/m | 0.261 | 0.000 | 0.000 |
| 机非分隔带宽度/m | 0.048 | 0.036 | 0.000 |
| 中央分隔带宽度/m | 0.054 | 0.022 | 0.033 |
| 双向车道数 | 0.003 | 0.003 | 0.003 |
| 车道平均宽度/m | 0.004 | 0.004 | 0.004 |
| 单侧渠化宽度/m | 0.037 | 0.022 | 0.015 |
| 绿化率/% | 0.010 | 0.007 | 0.008 |
| 人行道宽度/m | 0.024 | 0.012 | 0.018 |
| 横坡度/% | 0.017 | 0.010 | 0.015 |
| 公交港湾宽度/m | 0.058 | 0.035 | 0.000 |
| 管线距离道路中心长度/m | 0.015 | 0.008 | 0.012 |
| 道路1 km造价/万元 | 0.004 | 0.004 | 0.004 |
| 综合评价值F | 0.828 | 0.452 | 0.136 |
在实例中,当道路规划红线宽度相同时,3个设计方案权重较大的指标主要有分隔带的宽度大小、是否有公交港湾等;权重较小的指标主要有车道数和通行能力。这是因为当道路红线宽度确定后,机动车道数目和交叉口间距等因素在各个方案中差异较小,导致路段通行能力相近,故权重较小;在市政道路设计中,单位造价对城市道路横断面方案决策的敏感度较低,权重也较小。据此可得出方案选择应主要考虑人、非机动车、机动车是否分离,是否设置公交专用道和港湾式公交停靠站,路权是否明确,交叉口是否渠化以及横断面布局与管线之间关系是否合适等因素。评价指标的权重值与各方案相应评价指标的相对隶属度值相乘并累加,可得模糊评价的综合指标值,该值越大说明方案的优越性越大。从表 2的结果可以得出,方案1为最优方案。该道路以方案1作为最终方案,道路建成后运营状况良好,体现了评价方法的合理性和实用性。
5 结论(1) 在分析城市道路横断面设计的影响因素的基础上,遴选主要因素构建了包括交通需求、道路设计、环境及人性化要求等子项目在内的横断面设计评价指标体系。
(2) 对大量数据进行量化后,利用相对隶属度矩阵构造权重矩阵,一方面作为一种改进后的横断面模糊评价方法,另一方面可以作为对专家打分法等主观构造权重矩阵方法的验证,适合于市政道路横断面设计与分析评价。
(3) 利用改进的层次分析法,构建量化的权重矩阵,减少了主观因素对方案选择的影响,对城市道路横断面设计方案的比选具有一定的实用性。
| [1] | 徐吉谦. 关于城市道路规划设计几个问题的探讨[J]. 城市道桥与防洪 , 2001 (2) : 1-6 XU Ji-qian. Approach to Several Problems of Urban Road Planning Design[J]. Urban Roads Bridges & Flood Control , 2001 (2) : 1-6 |
| [2] | 李朝阳, 徐循初. 城市道路横断面规划设计研究[J]. 城市规划汇刊 , 2001 (2) : 47-52 LI Zhao-yang, XU Xun-chu. The Study on the Planning and Design of Urban Road Cross-section[J]. Urban Planning Forum , 2001 (2) : 47-52 |
| [3] | 万浴虎.城市道路横断面规划设计方法及应用研究[D].南京:东南大学, 2003. WAN Yu-hu. Research on Design Method and Application of Urban Road Cross-section Planning[D].Nanjing:Southeast University, 2003. |
| [4] | 熊德国, 鲜学福. 模糊综合评价方法的改进[J]. 重庆大学学报:自然科学版 , 2003, 26 (6) : 93-95 XIONG De-guo, XIAN Xue-fu. Improvement of Fuzzy Comprehensive Evaluation Method[J]. Journal of Chongqing University:Natural Science Edition , 2003, 26 (6) : 93-95 |
| [5] | 梁军, 江薇, 李旭宏. 模糊综合评价方法改进及其在交通管理规划中的应用[J]. 交通运输工程学报 , 2002, 2 (4) : 68-72 LIANG Jun, JIANG Wei, LI Xu-hong. An Improvement on Fuzzy Comprehensive Evaluation Method and Its Use in Urban Traffic Planning[J]. Journal of Traffic and Transportation Engineering , 2002, 2 (4) : 68-72 |
| [6] | 偶昌宝, 卓敏. 多级模糊综合评判在城市道路横断面方案评价中的应用[J]. 北方交通 , 2011 (11) : 1-5 OU Chang-bao, ZHUO Min. Application of Multi-level Fuzzy Comprehensive Evaluation in Cross Section Scheme Evaluation of Urban Road[J]. Northern Commu-nications , 2011 (11) : 1-5 |
| [7] | 王晓华, 于明明, 王朝辉. 绿色生态型城市道路横断面优化体系研究[J]. 城市道桥与防洪 , 2013 (1) : 118-121 WANG Xiao-hua, YU Ming-ming, WANG Zhao-hui. Study on Cross Sectional Optimization System of Green Ecotype Urban Road[J]. Urban Roads Bridges & Flood Control , 2013 (1) : 118-121 |
| [8] | 杨静, 石俊刚. 城市道路横断面设计微观评价方法[J]. 科学技术与工程 , 2014, 14 (22) : 299-302 YANG Jing, SHI Jun-gang. A Microcosmic Evaluation Methodology for Cross-section Design of Urban Road[J]. Science Technology and Engineering , 2014, 14 (22) : 299-302 |
| [9] | 文国玮. 城市交通与道路系统规划[M]. 北京: 清华大学出版社, 2001 . WEN Guo-wei. The Urban Traffic and Road System planning[M]. Beijing: Tsinghua University Press, 2001 . |
| [10] | CJJ 37-2012, 城市道路工程设计规范[S]. CJJ 37-2012, Code for Design of Urban Road Engineering[S]. http://www.doc88.com/p-678855336646.html |
| [11] | LEVINSON H S. Street Spacing and Scale[J]. Transportation Research Circular , 2000, C019 : 1-16 |
| [12] | 郭亚军. 综合评价理论与方法[M]. 北京: 科学出版社, 2002 . GUO Ya-jun. Comprehensive Evaluation Theory and Method[M]. Beijing: Science and Technology Press, 2002 . |
| [13] | 彭祖赠, 孙韫玉. 模糊(Fuzzy)数学及其应用[M]. 武汉: 武汉大学出版社, 2003 . PENG Zu-zeng, SUN Yun-yu. Fuzzy Mathematics and Its Application[M]. Wuhan: Wuhan University Press, 2003 . |
| [14] | 李洪兴, 汪培庄. 模糊数学[M]. 北京: 国防工业出版社, 1994 . LI Hong-xing, WANG Pei-zhuang. Fuzzy Mathematics[M]. Beijing: National Defence Industry Press, 1994 . |
| [15] | 刘万里, 雷治军. 关于AHP中判断矩阵校正方法的研究[J]. 系统工程理论与实践 , 1997, 17 (6) : 30-34, 39 LIU Wan-li, LEI Zhi-jun. Study on Rectification Method for the Judgment Matrix in AHP[J]. Systems Engineering-Theory & Practice , 1997, 17 (6) : 30-34, 39 |
 2016, Vol. 33
2016, Vol. 33
