扩展功能
文章信息
- 石陆魁, 周浩, 刘文浩
- SHI Lu-kui, ZHOU Hao, LIU Wen-hao
- 基于流形学习的路面破损图像多特征融合与可视化
- Multi-feature Fusion and Visualization of Pavement Distress Images Based on Manifold Learning
- 公路交通科技, 2016, 33(11): 26-33
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 26-33
- 10.3969/j.issn.1002-0268.2016.11.005
-
文章历史
- 收稿日期: 2015-12-30
2. 河北省大数据计算重点实验室, 天津 300401
2. Hebei Provincial Key Liboratory of Big Data Calculation, Tianjin 300401, China
随着公路交通建设的快速发展,道路维护与管理问题日趋突出。因此,检测路面破损情况对道路维护来说是一项至关重要的工作,而传统的人工检测早已不能满足道路交通发展的要求。随着图像处理技术的不断发展,基于图像处理的路面破损自动检测方法不断涌现。文献[1]提出了用不变矩特征来识别沥青路面破损图像;文献[2]提出了基于混合密度因子的路面破损图像识别方法;文献[3]使用Beamlet变换提取路面裂缝的线性特征后用神经网络进行分类;文献[4]利用中值滤波和Hessian矩阵的多线性滤波器对路面图像预处理后再自动检测路面裂缝;文献[5]使用小波变换结合神经网络检测路面裂缝类别;文献[6-7]提出了利用连通域的方法来提取裂缝;文献[8]提出了用几何特征来识别水泥刻槽;文献[9-10]提出了利用支持向量机来识别路面裂缝;文献[11]提出了利用双相扫描检测来识别三维裂缝。在多数路面破损图像的自动识别中,通常是采用某种方法提取路面图像的特征,然后用BP (Back Propagation)神经网络、支持向量机(Support Vector Machine,SVM)、K近邻(K-Nearest Neighbor,KNN)和极限学习机(Extreme Learning Machine,ELM)[12]等方法进行识别。路面破损图像的特征提取对识别至关重要,是自动检测的关键。
目前,用于描述路面破损的特征主要有二值图像的投影、不变矩、纹理、密度因子等[13]。由于路面破损图像的复杂性、噪声的影响和这些特征的局限性,使用单一特征很难充分描述路面破损图像的全部信息,而且特征的物理意义也不太明显。多种特征的线性组合虽然在一定程度上提高了识别精度,但忽视了非线性的特征信息,丢失了多特征间的内在联系,同时增加了数据的维数,可能会导致维数灾难,这些问题都对分类结果造成了影响。为此引入流形学习对多种特征进行融合[14-16],以获取路面破损图像的本质特征。
流形学习的目标是发现隐藏在高维数据中的低维流形,它在图像处理、数据挖掘、机器学习、模式识别等领域得到了广泛应用[17]。目前,具有代表性的流形学习方法有等距映射法(Isometric Feature Mapping, ISOMAP)[18]、局部线性嵌入法(Locally Linear Embedding, LLE)[19]、拉普拉斯特征映射法(Laplacian Eigenmaps, LE)[20]和局部切空间校正法(Local Tangent Space Alignment,LTSA)[21]等。在多数流形学习算法中,都需要确定样本的k个近邻,为了利用流形学习获得高维数据的本质特征,选择合适的距离措施来选择邻域是非常重要的,4.2中的试验也说明了这一点。
为了较为充分地描述路面破损图像的信息,发掘多种特征之间的内在联系,避免组合多种特征导致的维数灾难问题,本文提出一种基于流形学习的路面破损图像多特征融合方法,使用不同的分类方法对融合后的特征进行分类,以有效地提高路面破损图像的分类精度,实现高维数据的可视化。
1 路面破损图像特征提取方法常见的路面破损情况有横向裂缝、纵向裂缝、网状裂缝、块状裂缝和坑槽等。特征提取是实现路面破损图像自动检测的关键。本文使用投影、混合密度因子和二阶不变矩3种特征提取方法,提取8个路面破损图像特征。
1.1 投影理论路面裂缝的二值图像投影既降低了原始图像的维数,又反映了目标的分布情况。对路面破损图像二值化处理后,分别使用1和0作为破损区域和背景区域的像素值。设路面破损图像的二值图像为G,用g(i, j)表示像素值,大小为M×N,图像G在x轴和y轴上的投影量分别为[13]:
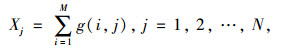
|
(1) |
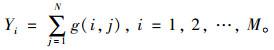
|
(2) |
由于横向裂缝和纵向裂缝在x轴与y轴的投影量最大差值相对较大,其他类别裂缝的最大差值较小,所以把二值图像在x轴与y轴的投影量最大差值作为路面破损图像的特征,记为(C1, C2),其计算公式[13]分别为:
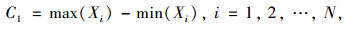
|
(3) |

|
(4) |
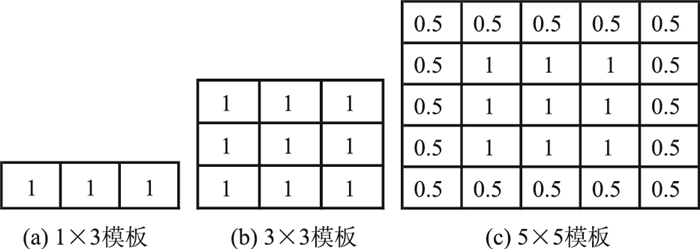
混合破损密度因子[22]是一种基于路面图像子块的方法,文献[2]中提出了破损密度因子分别为1×3,3×3,5×5的模板算子,如图 1所示。扫描0,1子块化后的路面图像,对于0子块,不做处理;对于1子块,使用模板算子与其进行卷积。利用3个模板算子与二值化图像分别进行卷积后得到S1,S3,S5。设原二值化路面图像中1子块的总和为S0,并把S0作为一个路面破损图像特征记为C3,把S0与卷积的计算结果作为路面破损图像的特征,记为(C4, C5, C6),其计算公式如下[2]:
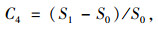
|
(5) |
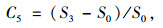
|
(6) |
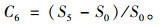
|
(7) |
|
| 图 1 3种大小不同的破损密度因子 Fig. 1 Distress density factors with 3 sizes |
| |
本文利用破损密度因子与二值化处理后的二值矩阵直接进行卷积运算,得到上述4个特征。
1.3 二阶不变矩基于二阶矩的不变矩表示二维目标图像的大小和方向,可以较好地区分网状裂缝和块状裂缝[23]。因此本文选取Hu不变矩的二阶不变矩φ1和φ2作为路面破损图像的特征,记为(C7, C8)。设f(x, y)为图像的二维函数,大小为M×N,其二阶不变矩定义如下[23]:
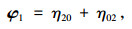
|
(8) |
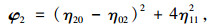
|
(9) |
式中ηpq为归一化的中心矩,计算公式为:
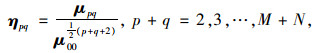
|
(10) |
式中μpq为中心矩。
2 流形学习算法本文利用流形学习实现多种路面破损图像特征的融合和可视化,下面简要介绍试验中用到的几种流形学习算法。
2.1 ISOMAP算法ISOMAP算法的主要思想是用测地线距离来代替欧氏距离,其步骤如下[18]:
(1) 构建邻域图。计算所有样本点之间的距离,选择k个最近邻或某个邻域半径γ内的所有点作为邻域。
(2) 估计测地线距离。若两个样本为近邻,则测地线距离即为输入空间的距离;若样本点为非近邻关系,则测地线距离用邻域图上两点间的最短路径近似。
(3) 应用多维尺度分析法计算d维嵌入。
2.2 LLE算法LLE算法的基本思想是假设每个样本和它的近邻点在一个线性的或者近似线性的局部区域中,其步骤如下[19]:
(1) 确定邻域。采用与ISOMAP算法中相同的方法来确定每个样本的邻域。
(2) 计算重构权值矩阵。重构权值矩阵W可以通过在最小二乘意义下最小化每个样本点重构误差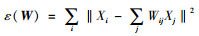
(3) 构造低维嵌入。通过极小化损失函数ε(Y)=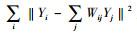
LE算法的主要目标是使得高维空间中距离很近的点在低维空间中也离得很近,其步骤如下[20]:
(1) 构建邻域图。采用与ISOMAP算法中相同的方法来确定每个样本的邻域。
(2) 计算权值矩阵W。利用热核方程或者简单方法确定权值。
(3) 计算低维坐标。通过求解推广的特征值问题来得到低维坐标。
2.4 LTSA算法LTSA算法利用局部邻域的切空间表示样本的邻域,构建样本的局部切空间,最后排列切空间来获取全局的低维坐标。LTSA算法的步骤如下[21]:
(1) 确定邻域。采用与ISOMAP算法中相同的方法来确定每个样本的邻域。
(2) 构建局部切空间。利用奇异值分解中心化后的邻域矩阵,得到局部切空间坐标。
(3) 获取全局低维嵌入坐标。排列局部坐标获得全局最优的低维嵌入坐标。
3 基于流形学习的多特征融合在路面破损图像自动识别中,通常通过组合多种特征来提高识别精度。组合多种特征一方面增加了特征数据的维数,另一方面丢失了多种特征之间的内在联系。因此,有必要对路面破损图像识别中的多种特征进行内在融合,发现其物理意义,而不是简单地进行线性组合。
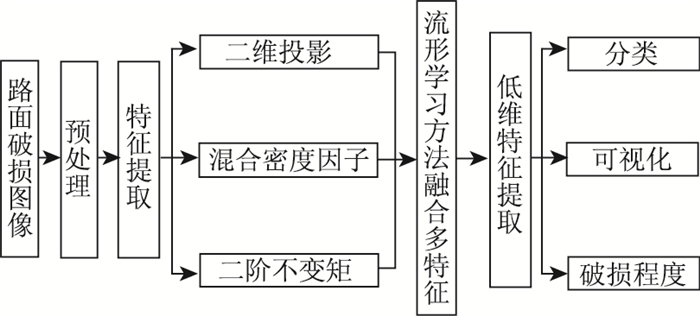
多种特征组合后的数据可以看作是嵌入在高维空间中的低维流形,利用流形学习可以发现其内在结构。为此,将特征融合与流形学习相结合,提出了一种基于流形学习的多特征融合方法。该方法利用流形学习将组合后的高维特征数据映射到低维空间中,提取路面破损图像的本质特征,实现多种特征的内在融合,并对融合后的低维特征进行裂缝识别,最后利用低维特征实现路面破损图像的可视化。基于流形学习的多特征融合模型如图 2所示。
|
| 图 2 基于流形学习的多特征融合模型 Fig. 2 Multi-feature fusing model based on manifold learning |
| |
为了得到有利于路面破损图像自动检测的特征,在该模型中需要对路面破损图像做下列处理。
(1) 预处理。利用直方图均衡化对图像进行增强,然后使用中值滤波对路面破损图像去噪,再经过二值化处理得到二值化图像。
(2) 特征提取。利用不同的路面破损图像特征提取方法对预处理后的二值化图像提取特征。该模型中分别应用投影理论、混合密度因子、二阶不变矩3种特征提取方法从预处理后的二值图像中提取特征,得到2个投影特征、4个密度因子特征和2个二阶不变矩特征,将这8个特征组成特征向量,记为C=(C1, C2, C3, C4, C5, C6, C7, C8)。对待处理的图像提取特征,得到包含N个样本的数据集T={T1, T2, …, TN},每个Ti都是1个八维的特征向量。
(3) 多特征融合。利用流形学习方法提取路面破损图像的本质特征,将八维的多特征数据映射为二维特征,流形学习方法可以使用ISOMAP、LLE、LE和LTSA等。后面的试验表明用LE算法提取数据的低维特征识别效果最好,同时用相交距离选择邻域比用欧式距离选择邻域更加有效。从直方图相交算法得到相交距离的定义如下:
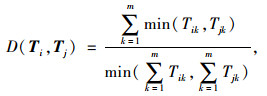
|
(11) |
式中,Ti, Tj∈T为数据集中的样本点;Tik和Tjk分别为第i个和第j个样本的第k个属性;m为特征向量中的特征个数,在试验中m=8。
获得低维特征后可以完成下列任务:
(1) 识别路面破损图像的类别。可以利用ELM,KNN,SVM和BP神经网络等分类器以融合后的低维特征作为输入参数,识别破损类别。
(2) 路面破损图像的可视化。将融合后的低维特征映射到低维空间中,实现高维数据的可视化,分析每个特征的物理含义。
(3) 分析路面破损程度。路面破损图像可视化后,根据每个特征的物理含义和其在裂缝类别分布图中的分布情况,可以定性分析路面图像的破损程度。
4 结果与讨论为了验证所提方法的有效性,在实际采集的路面破损图像数据集上进行测试。数据集中包含360幅路面破损图像,分为4类,分别为横向裂缝、纵向裂缝、网状裂缝和块状裂缝,每类都包含90幅图像。在试验中首先对每幅图像进行预处理,预处理过程包括直方图均衡化、中值滤波和二值化,预处理后得到360幅二值图像作为后续试验数据。
试验包括4部分:多种特征组合对识别精度的影响、不同流形学习方法的比较及参数选择、基于流形学习的多特征融合有效性验证、路面破损图像的可视化分析。在试验中使用三折交叉验证法进行测试,将数据集分成3组,其中1组作为测试集,另外两组作为训练集,轮流进行,取3次测试的平均值作为最终结果。
4.1 多种特征组合对识别精度的影响为了验证多种特征组合后能否提高分类精度,首先对预处理后的图像分别提取投影特征、混合密度因子特征和二阶不变矩特征,然后用不同分类方法对单一特征进行识别,再对3种特征进行不同方式的组合后分类,分类方法包括ELM,KNN,SVM和BP神经网络,结果如表 1所示。试验中,ELM的隐含层参数h=21;KNN的近邻个数k=5;SVM模型类型采用v-SVC模型,核函数采用径向基核函数(Radial Basis Function,RBF),参数n=0.4,g=0.008 4;BP神经网络迭代1 000次,学习率η=0.1。
| 特征组合方式 | ELM | KNN | SVM | BP |
| 投影 | 85.83 | 85.83 | 84.72 | 70.27 |
| 混合密度因子 | 85.83 | 82.77 | 84.44 | 71.38 |
| 二阶不变矩 | 78.33 | 73.89 | 77.22 | 53.06 |
| 投影+混合密度因子 | 89.16 | 87.50 | 87.76 | 73.88 |
| 投影+二阶不变矩 | 87.50 | 85.83 | 85.56 | 71.56 |
| 混合密度因子+二阶不变矩 | 87.22 | 85.83 | 87.78 | 71.94 |
| 三类特征组合 | 89.72 | 87.50 | 88.33 | 76.11 |
| 注:“投影+混合密度因子”表示将投影特征和混合密度因子特征组合作为特征数据。 | ||||
从表 1可以看出,使用ELM,SVM和BP神经网络分类器对单类特征的分类精度低于两两组合的精度,而3种特征组合的精度又高于两两组合的结果;KNN分类器对投影特征和混合密度因子特征分别与不变矩组合的分类精度和单独使用投影特征分类结果相同,但3种特征组合的分类精度要高于其他特征组合方式的结果。由此说明,可以通过组合多种路面破损图像特征来提高分类精度。
4.2 不同流形学习方法的比较及参数选择流形学习算法中有两个参数需要确定,一个是邻域参数k,另一个是本征维数d。在此,用试验来确定这两个参数,同时比较不同流形学习方法融合多种特征的效果。
首先,比较不同邻域参数k对流形学习方法的影响,并估计本征维数d,以LE算法为例来说明。利用LE算法对组合3种特征得到的八维数据进行融合,选取d=2和d=3,用KNN分类器对二维和三维特征分别进行裂缝类别识别,结果如表 2所示。试验中,KNN分类器的近邻个数为5,执行LE算法时采用相交距离选择邻域,k∈[3, 12]。
| k | d=2 | d=3 | k | d=2 | d=3 |
| 3 | 93.06 | 93.06 | 8 | 94.72 | 95.00 |
| 4 | 94.17 | 93.33 | 9 | 94.44 | 95.00 |
| 5 | 95.00 | 94.44 | 10 | 94.72 | 95.00 |
| 6 | 93.33 | 93.61 | 11 | 94.17 | 94.72 |
| 7 | 93.61 | 94.44 | 12 | 94.44 | 94.44 |
从表 2中可以看出,邻域参数k在取值范围内都获得了较好的结果,而且维数d=2和d=3相差不大。因此,k可以在3~12之间选择,d可以选择2。在后面的试验中,LE算法中k=5。同样可得到ISOMAP算法中k=11,LLE算法中k=10,由于LTSA邻域参数小于23时出现奇异矩阵,所以LTSA算法中取k=25。
为了比较不同的流形学习算法融合多特征的效果,采用ISOMAP,LLE,LE和LTSA这4种流形学习算法分别对组合3种特征得到的八维数据进行融合,本征维数d取2和3。同时为了比较采用不同距离措施选择邻域对分类结果的影响,在流形学习方法中分别使用欧氏距离和相交距离选择邻域。用KNN分类器对多种流形学习方法提取的特征进行分类,比较其结果,试验结果如表 3所示。在试验中,KNN分类器的近邻个数为5。
| 维数+距离 | ISOMAP | LLE | LE | LTSA |
| 2+欧氏距离 | 85.28 | 85.27 | 86.67 | 79.72 |
| 2+相交距离 | 90.28 | 83.06 | 95.00 | 81.39 |
| 3+欧氏距离 | 89.17 | 88.06 | 87.50 | 86.67 |
| 3+相交距离 | 90.56 | 88.06 | 94.44 | 88.06 |
| 注:“2+欧式距离”表示执行流形学习方法时用欧式距离选择邻域,d=2。 | ||||
表 3中的试验结果表明,整体上4种流形学习方法中选择相同的维数d,使用相交距离选择邻域比欧氏距离具有更高的识别精度;在距离措施相同的条件下,采用三维特征的识别精度要高于二维的。不管采用哪种距离措施和选择几维数据作为特征,多数情况下利用LE算法融合多种特征的识别精度均高于其他流形学习方法,而且也远高于3种特征组合后直接分类的结果。同时LE算法使用相交距离选择邻域,d=2时,识别精度与三维非常相近。
结合表 2和表 3,在后面的试验中采用LE算法对多特征进行融合,低维维数d选取2,用相交距离选择邻域。
4.3 基于流形学习的多特征融合为了进一步验证所提方法的有效性,首先利用LE方法从3种特征组合后的八维数据中提取出二维特征,然后使用上述4种分类器识别破损类别,最后计算各个类别的召回率、查准率、F值和总的分类精度。试验中各参数选择与4.1和4.2中相同,结果如表 4~表 7所示。
| 算法 | 横向 | 纵向 | 网状 | 块状 |
| ELM | 90.00 | 88.89 | 92.22 | 85.56 |
| LE+ELM | 96.67 | 94.44 | 95.56 | 94.44 |
| KNN | 91.11 | 85.56 | 93.33 | 80.00 |
| LE+KNN | 96.67 | 93.33 | 95.56 | 94.44 |
| SVM | 91.11 | 86.67 | 93.33 | 82.22 |
| LE+SVM | 96.67 | 92.22 | 92.22 | 93.33 |
| BP | 74.18 | 85.56 | 82.22 | 64.18 |
| LE+BP | 93.33 | 88.89 | 94.44 | 84.76 |
| 注:“LE+ELM”表示采用LE算法融合特征,使用ELM分类器识别裂缝类别,下同。 | ||||
| 算法 | 横向 | 纵向 | 网状 | 块状 |
| ELM | 91.82 | 90.35 | 91.35 | 85.36 |
| LE+ELM | 98.92 | 96.63 | 97.70 | 88.95 |
| KNN | 87.52 | 94.21 | 91.33 | 79.75 |
| LE+KNN | 97.85 | 96.66 | 94.48 | 92.14 |
| SVM | 87.65 | 92.96 | 91.32 | 83.52 |
| LE+SVM | 93.60 | 98.81 | 96.47 | 86.77 |
| BP | 94.75 | 72.83 | 64.27 | 86.13 |
| LE+BP | 100.00 | 89.80 | 85.18 | 88.95 |
| 算法 | 横向 | 纵向 | 网状 | 块状 |
| ELM | 90.44 | 89.46 | 91.75 | 85.16 |
| LE+ELM | 97.70 | 95.48 | 96.61 | 91.48 |
| KNN | 89.14 | 89.36 | 92.31 | 79.29 |
| LE+KNN | 97.15 | 94.91 | 95.01 | 93.09 |
| SVM | 89.09 | 89.65 | 92.29 | 82.43 |
| LE+SVM | 95.04 | 95.38 | 94.29 | 89.87 |
| BP | 82.76 | 78.64 | 71.98 | 72.70 |
| LE+BP | 96.47 | 89.08 | 89.55 | 86.31 |
| ELM | KNN | SVM | BP | |
| 直接分类 | 89.72 | 87.50 | 88.33 | 76.11 |
| LE降维 | 95.28 | 95.00 | 94.72 | 91.39 |
表 4~表 7中的试验结果表明,与组合3种特征直接分类相比,经过LE算法降维融合后,4种类别的路面裂缝具有更高的召回率、查准率和分类精度,尤其是极大地提高了纵向裂缝和块状裂缝的召回率、横向裂缝和网状裂缝的查准率。经过LE算法融合后得到的二维特征数据具有更强的鲁棒性,采用4种分类器都能得到较高的识别精度。
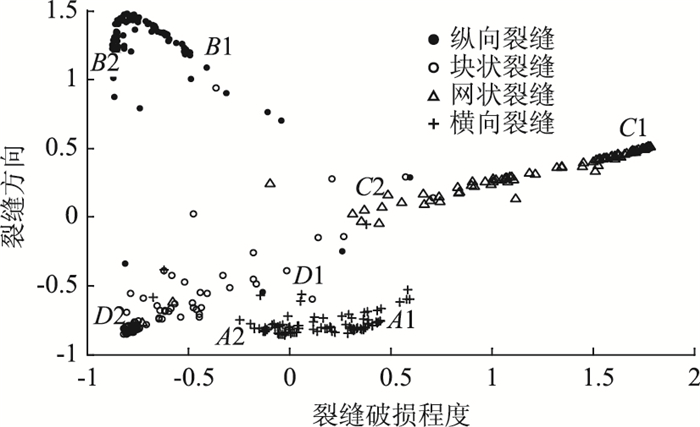
4.4 路面破损图像的可视化在试验中,使用LE算法对提取的3种路面破损图像特征组合成的八维特征向量进行融合,得到一个全新的二维特征向量,将此二维特征向量映射到二维空间中,得到如图 3所示的4类路面裂缝分布图。
|
| 图 3 路面裂缝类别分布图 Fig. 3 Distribution diagram of pavement crack categories |
| |
在图 3中,4个类别的裂缝分别处于不同的区域中。通过对照二维分布图和路面破损图像可以看出,第1维特征(水平方向坐标)可以表示裂缝的破损程度和多向裂缝线条的复杂程度,随着水平方向坐标的增大,裂缝由块状逐渐变成网状,裂缝数越来越多,并且裂缝随着坐标值的增大其破损程度也增大。点D2,D1,C2,C1对应的路面图像为图 4(a)~(d)。第2维特征(垂直方向坐标)表示裂缝方向,随着坐标值的增大,裂缝类别由横向裂缝逐渐向纵向裂缝变化,如点A2,A1,B2,B1,其对应的路面图形为图 4(e)~(h)。从路面破损图像的二维分布图不但可以看出图像所属的破损类别,而且可以看出路面的破损程度,因此可以利用第1维特征来定性分析路面的破损程度,当达到一定的阈值后再具体计算其破损面积、大小等。

|
| 图 4 裂缝走向和破损程度分析图例 Fig. 4 Instances of crack direction and distress analysis |
| |
5 结论
路面破损情况检测为道路维护工作提供了重要依据。由于路面破损种类多样,图像噪音复杂,很难用单一特征来充分描述路面破损图像的信息。针对路面破损图像识别中特征提取方法的多样性和线性特征组合的高维度问题,提出了一种基于流形学习的路面破损图像多特征融合方法,利用流形学习方法将多种特征融合在一起,实现了路面破损图像的可视化。试验结果表明,利用流形学习方法融合3种特征后提高了各类裂缝的召回率、查准率,尤其是极大地提高了纵向裂缝和块状裂缝的召回率、横向裂缝和网状裂缝的查准率,从而极大地提高了识别精度。以LE算法利用4种流形学习方法融合多种特征,得到了最好的结果。利用LE算法融合后得到的二维特征具有更强的鲁棒性,采用4种分类器都能得到较高的识别精度。利用LE算法融合多种特征时使用相交距离选择邻域比欧氏距离具有更高的识别精度。同时,通过可视化二维特征得到了特征的物理含义,为破损程度的定性分析提供了一个简单的依据。下一步的工作是将所提出的多特征融合方法应用在实际的路面破损图像检测系统中,检测其效果。
| [1] | 初秀民, 王荣本, 储江伟, 等. 基于不变矩特征的沥青路面破损图像识别[J]. 吉林大学学报:工学版 , 2003, 33 (1) : 1-7 CHU Xiu-min, WANG Rong-ben, CHU Jiang-wei, et al. Asphalt Pavement Surface Distress Image Recognition Based on Moment Invariant Feature[J]. Journal of Jilin University:Engineering and Technology Edition , 2003, 33 (1) : 1-7 |
| [2] | 肖旺新, 严新平, 张雪. 基于混合密度因子的路面破损自动识别研究[J]. 交通运输工程与信息学报 , 2005, 3 (2) : 19-26 XIAO Wang-xin, YAN Xin-ping, ZHANG Xue. Research on the Automatic Pavement Distress Recognition Based on Synthetical Distress Density Factor[J]. Journal of Transportation Engineering and Information , 2005, 3 (2) : 19-26 |
| [3] | YING L, SALARI E. Beamlet Transform-Based Technique for Pavement Crack Detection and Classification[J]. Computer-Aided Civil and Infrastructure Engineering , 2010, 25 (8) : 572-580 |
| [4] | FUJITA Y, HAMAMOTO Y. A Robust Automatic Crack Detection Method from Noisy Concrete Surfaces[J]. Machine Vision and Applications , 2011, 22 (2) : 245-254 |
| [5] | NEJAD F M, ZAKERI H. An Expert System Based on Wavelet Transform and Radon Neural Network for Pavement Distress Classification[J]. Expert Systems with Applications , 2011, 38 (6) : 7088-7101 |
| [6] | 于泳波, 李万恒, 张劲泉, 等. 基于图像连通域的桥梁裂缝提取方法[J]. 公路交通科技 , 2011, 28 (7) : 90-93 YU Yong-bo, LI Wan-heng, ZHANG Jin-quan, et al. Bridge Cracks Extraction Method Based on Image Connected Domain[J]. Journal of Highway and Transportation Research and Development , 2011, 28 (7) : 90-93 |
| [7] | 马荣贵, 徐琨, 刘飞飞. 高速公路路面裂缝识别算法研究[J]. 交通信息与安全 , 2014, 32 (2) : 90-94 MA Rong-gui, XU Kun, LIU Fei-fei. Highway Surface Crack Image Identifying Algorithm[J]. Journal of Transport Information and Safety , 2014, 32 (2) : 90-94 |
| [8] | 荣婧, 潘玉利. 基于图像的水泥刻槽路面裂缝识别方法[J]. 公路交通科技 , 2012, 29 (3) : 45-50 RONG Jing, PAN Yu-li. Digital Image Based Crack Detection of Grooved Cement Concrete Pavement[J]. Journal of Highway and Transportation Research and Development , 2012, 29 (3) : 45-50 |
| [9] | OLIVEIRA H, CORREIA P L. Automatic Road Crack Detection and Characterization[J]. IEEE Transactions on Intelligent Transportation Systems , 2013, 14 (1) : 155-168 |
| [10] | 沈照庆, 彭余华, 舒宁. 一种基于SVM的路面影像损伤跨尺度识别方法[J]. 武汉大学学报:信息科学版 , 2013, 38 (8) : 993-997 SHEN Zhao-qing, PENG Yu-hua, SHU Ning. A Road Damage Identification Method Based on Scale-span Image and SVM[J]. Geomatics and Information Science of Wuhan University , 2013, 38 (8) : 993-997 |
| [11] | 孙朝云, 赵海伟, 李伟, 等. 基于双相扫描检测的路面三维裂缝识别方法[J]. 中国公路学报 , 2015, 28 (2) : 26-32 SUN Zhao-yun, ZHAO Hai-wei, LI Wei, et al. 3D Pavement Crack Identification Method Based on Dual-phase Scanning Detection[J]. China Journal of Highway and Transport , 2015, 28 (2) : 26-32 |
| [12] | HUANG G B, ZHOU H, DING X, et al. Extreme Learning Machine for Regression and Multiclass Classification[J]. IEEE Transactions on Systems, Man, & Cybernetics Part B:Cybernetics , 2012, 42 (2) : 513-529 |
| [13] | ZUO Y X, WANG G Q, ZUO C C. The Segmentation Algorithm for Pavement Cracking Images Based on the Improved Fuzzy Clustering[J]. Applied Mechanics and Materials , 2013, 319 : 362-366 |
| [14] | RADUCANU B, DORNAIKA F. A Supervised Non-linear Dimensionality Reduction Approach for Manifold Learning[J]. Pattern Recognition , 2012, 45 (6) : 2432-2444 |
| [15] | SUN B Y, ZHANG X M, LI J, et al. Feature Fusion Using Locally Linear Embedding for Classification[J]. IEEE Transactions on Neural Networks , 2010, 21 (1) : 163-168 |
| [16] | 胡建中, 吴瑶, 谢小欣. 一种基于LLE特征融合的故障识别方法[J]. 中国机械工程 , 2013, 24 (24) : 3345-3348 HU Jian-zhong, WU Yao, XIE Xiao-xin. A Method for Fault Recognition Based on LLE Feature Fusion[J]. China Mechanical Engineering , 2013, 24 (24) : 3345-3348 |
| [17] | CRIMINISI A, SHOTTON J, KONUKOGLU E. Decision Forests:A Unified Framework for Classification, Regression, Density Estimation, Manifold Learning and Semi-Supervised Learning[J]. Foundations and Trends in Computer Graphics and Vision , 2012, 7 (2/3) : 81-227 |
| [18] | TENENBAUM J B, DE SILVA V, LANGFORD J C. A Global Geometric Framework for Nonlinear Dimensionality Reduction[J]. Science , 2000, 290 (5500) : 2319-2323 |
| [19] | ROWEIS S T, SAUL L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science , 2000, 290 (5500) : 2323-2326 |
| [20] | BELKIN M, NIYOGI P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation[J]. Neural Computation , 2003, 15 (6) : 1373-1396 |
| [21] | ZHANG Z Y, ZHA H Y. Principal Manifolds and Nonlinear Dimensionality Reduction via Local Tangent Space Alignment[J]. Journal of Shanghai University , 2004, 26 (4) : 406-424 |
| [22] | 肖旺新, 张雪, 黄卫, 等. 路面破损自动识别的一种新算法[J]. 公路交通科技 , 2005, 22 (11) : 75-78 XIAO Wang-xin, ZHANG Xue, HUANG Wei, et al. One New Algorithm of Automatic Classification for Pavement Distress[J]. Journal of Highway and Transportation Research and Development , 2005, 22 (11) : 75-78 |
| [23] | 刘国海, 蒋志佳. 基于改进ART-2网络和不变矩的高压瓷瓶裂缝识别[J]. 器仪表学报 , 2009, 30 (7) : 1420-1425 LIU Guo-hai, JIANG Zhi-jia. Recognition of Porcelain Bottle Crack Based on Modified ART-2 Network and Invariant Moment[J]. Chinese Journal of Scientific Instrument , 2009, 30 (7) : 1420-1425 |
 2016, Vol. 33
2016, Vol. 33
