扩展功能
文章信息
- 常连玉, 陈海燕
- CHANG Lian-yu, CHEN Hai-yan
- 无车承运人运力资源组织优化研究
- Study on Optimal Organization of Transport Resources for No-car Operating Carrier
- 公路交通科技, 2016, 33(10): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 152-158
- 10.3969/j.issn.1002-0268.2016.10.024
-
文章历史
- 收稿日期: 2016-03-02
2. 交通运输部管理干部学院, 北京 065201
2. Management Institute, Ministry of Transport, Beijing 065201, China
无车承运人是指公路货运市场以承运人的名义承揽货源,与货主方签订运输合同,然后无车承运人将货源外包给实际承运人,并与实际承运人签订运输合同,由实际承运人按照无车承运人的要求完成运输服务[1]。无车承运人模式的典型特征在于“承运人”,即区别于普通货运中介,它需要承担运输合同约定的法律责任,而“无车”是指一般不从事具体的运输业务,主要从事运输组织、货物分拨、运输方式和运输线路的选择等工作。一方面由无车承运人与分散的、规模较小的运输企业或运输个体签署合作协议,由这些分散的、规模较小的运输企业或运输个体作为实际承运人,承担实际运输任务,无车承运人则负责提供货运任务,车辆的组织调配和信息技术支持。另一方面,无车承运人则以其名义负责寻找货源,与货主签署运输合同,并承担承运人的权利和义务。这种运输组织模式比较适合货源相对集中,而运输企业力量相对薄弱、分散的运输市场,无车承运人通过联合小、散、弱的运输企业形成稳定合作关系,从而可以更好地满足货主(托运人)的需求,也同时可以为运输企业争取更合理的运价,有利于运输企业专注于运输环节,实现了专业化分工,提升运输市场的运作效率。在“互联网+”背景下,无车承运人利用信息技术平台整合车源和货源,进行有效匹配和高效运作,通过网络产生用户黏性,以运力整合和增值服务创造价值;通过合理组织资源和精细组织,低成本、高质量及高效率完成客户专业化与个性化的需求,为客户提供完整物流解决方案或供应链优化方案。
当前,我国物流企业中绝大部分是传统货运企业,物流运作水平不高,总体规模不大、组织化程度低,尤其是占市场主体90%以上的公路货运业户呈现典型的“多、小、散、弱”结构特点,导致全社会货源、运力、站场等物流资源集约利用不足、整体运作效率不高。无车承运人模式能够有效对接车、货资源,提升物流运作效率,降低车辆空驶率,提高组织化程度,降低社会和企业的物流成本。为此,交通运输部也将发展无车承运人作为推动运输服务提质增效升级的重点工作内容[2]。无车承运人在我国尚属新鲜事物,成熟的运作模式和成功经验较少,在推动无车承运人模式发展的过程中,要解决的核心问题就是无车承运人在承揽货源的基础上,利用科学的方法对其掌握的大量分散、差异化的运力资源进行高效组织配置,与货主个性化的运输需求进行合理匹配,这是降低运输成本,发挥无车承运人模式优势的关键。近年来,学术界对运力资源优化整合的运输系统决策问题逐渐有较多的关注,并且取得了一系列有价值的研究成果,但目前的研究主要集中在运输车辆调度、车辆路径优化、路径和调度的混合问题等方面。Alireza围绕多车场多周期和车辆容量及运行时间限制下,构建了总运输成本最小的模型[3]。侯爽在多车场协同工作背景下,针对多车场车辆路径问题和多车场车辆任务优化调度问题成本最优模型,提出了“先指派, 后优化”的多阶段启发式算法,结论证明模型及算法能够有效降低运输空驶率[4]。Repoussis的研究以降低运输总成本为目标,在运输需求已知的前提下,构建了车辆运行最优运输路线模型,优化了迭代禁忌搜索算法进行求解[5]。Subramanian针对混合车型车辆路径优化问题,设计根据不同车型确定最优车队构成并通过线路优化模型以实现总成本最优,并利用基于启发式的混合整数规划算法求解了360个客户运输优化问题,验证了模型的有效性[6]。Huth建立了在动态物流网络中,基于运力限制下车辆路径优化和物流资源调度的整合数学模型[7]。在多目标运力资源优化组织模型研究方面,Lin建立了企业物流资源与服务匹配导向下的多目标决策模型[8]。彭大衡、房巧红等基于机会约束下,建立了机会约束多目标规划模型,对资源组织情况进行优化,并通过算例对目标结构下的最优决策进行求解[9-10];分别针对物流车辆调度的单车、多车物流合乘匹配问题,以及在运输过程中的服务需求换乘和路网时变情况,构建了4类模型,并主要采用蚁群算法求解,通过算例证明模型能够降低车辆运输成本[11]。王旭提出面向物流任务的跨组织边界物流资源优化组织策略,建立以时间、成本、质量和服务为目标函数的包括车辆在内物流资源选择组织模型,并采用算法对模型进行求解[12]。
综上所述,现有文献主要是基于车辆路径优化(Vehicle Routing Problem,VRP)和车辆排程(Vehicle Scheduling Problem,VSP)扩展延伸发展起来,所构建的模型的目标函数更多考虑整体运输成本最低,缺少对无车承运人多方参与主体的分类研究,并且以研究单车场同质车辆(同一型号、载重量等)问题为主,而缺少对多车场异质车辆问题的研究。无车承运人的运力资源优化组织是一个复杂的系统工程,其运力资源和货源分布具有地理分散性、资源不平衡性、运力复杂性、主体相对独立性等特点。在对无车承运人运力资源进行优化的过程中,首先需要兼顾多主体利益,即无车承运人、运输车队(一般为服务于无车承运人的中小型企业)、货主三方要实现效益最大化。其次要符合运输市场实际情况,充分考虑分散的运力车型、载重能力等参差不齐,运价的形成和盈利模式,以及综合运输成本构成等情况。第三要结合无车承运人在对运力资源进行整合的同时也对货源分布进行整合,实现车货最优匹配。本文以此为出发点,构建带有机会约束条件无车承运人运力资源优化配置数学模型,为决策者提供参考,进而设计了微粒子群和神经网络混合智能算法进行求解,给出算例加以验证,该方法能够很好适应无车承运人运力和货运分散、个体独立、运力异构、整合增值等特点。
1 运力资源组织优化模型 1.1 问题描述将无车承运人运力资源组织优化问题定义为:某无车承运人在某一特定时期内在整个运输市场上主要为n个运输需求企业提供运输服务,这些运输需求企业共有A类货物需要运往特定目的地,运输距离分别为La,无车承运人与运输需求企业i谈判的第a(a∈A)类货物运输价格为pia,无车承运人合理安排运输车队j将运输需求企业i的货物a采用k种运输方式运送至目的地,无车承运人按照与车队j协定的价格Pj与该车队进行结算,该价格与pia之间一般存在差价,无车承运人达到其收益R的最大化。
1.2 基本假设本文在构建无车承运人运力资源组织优化模型时基于以下假设:
(1) 无车承运人在运输市场上可组织到一定规模的运力资源;
(2) 在货物装载过程中,均按照规定进行合理配装;
(3) 货物的运输均可按照运输需求企业的要求在指定的时间内运送至指定的目的地;
(4) 各种货物的货运量矩阵及起点和终点之间的距离矩阵均为已知。
1.3 模型构建无车承运人组织模式的关键是与运输需求企业签订运输合同,通过合理组织与无车承运人开展合作的运输车队或者企业的运力资源完成整个运输服务过程,因此无车承运人资源的组织优化涉及到运输市场上的3个主体:无车承运人、运输需求企业及运输车队或运输企业。无车承运人在取得货源的前提下,合理选择运输车队或企业进行价格谈判,通过与运输需求企业谈判的运输价格和与运输车队谈判的运输价格之间的差价赚取利润,并且期望利润最大化;对运输需求企业而言,其目的就是选择某种运输服务将货物在规定的时间内运至目的地;运输车队在买方市场的环境下,其目的是保证利润在一定的可接受水平内。因此,构建运力资源组织优化模型如下所示。
目标函数:
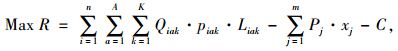
|
(1) |
约束条件:
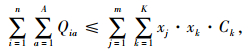
|
(2) |
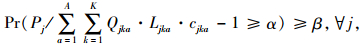
|
(3) |
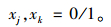
|
(4) |
模型中,R为无车承运人的收益;i为货物运输需求企业,n为货物运输需求企业总数;A为货物的种类数;K为运力类型总数;Qiak为货物运输需求企业i使用k种运力运输a类货物的需求量;Qia为运输需求企业i需要运输的a类货物的总量;piak为无车承运人针对采用k种运力运输a类货物向货物运输需求企业i收取的价格;Liak为货物运输需求企业i使用k种运力运输a类货物的运输距离;j为与无车承运人签订运输合作协议的车队或者运输企业;Ljka为车队j采用运输k种运力运输a类货物的实际运输距离;cjka为车队j采用运输k种运力运输a类货物运输价格;m为车队或者运输企业总数;Pj为无车承运人与j车队的结算价格;xj为逻辑变量,若无车承运人选取j车队合作,xj值则取1,否则取0;C为无车承运人的日常运营成本;Ck为k种运力的运输能力;xk为逻辑变量,α为车队j的利润率;β为置信水平。
式(1)为模型的目标函数,表示无车承运人的收益R最大化;式(2)为运力的容量限制,表示各类货物的载运量总和不超过各种运力的运输能力的总和;式(3)为机会约束条件,表示车队j的利润率不低于α的概率,不小于置信水平β;式(4)为对逻辑变量xj和xk的定义。
2 算法设计本文构建的模型为一个带有机会约束条件的非线性规划问题。考虑到微粒子群算法具有可实现且具有较小的调整参数、收敛速度快、解的质量高、鲁棒性较好等优点,而神经网络算法具有很强的非线性拟合能力、可映射任意复杂的非线性关系、学习规则简单等优点,因此采用微粒子群和神经网络混合智能算法求解该模型[13-15],具体算法步骤如下所示。
第1步:利用随机模拟为下列不确定函数U产生输入输出数据:(xt, yk),t,k分别为输入、输出神经元的个数。利用线性函数转换法对xt,yk分别进行归一化处理,以归一化后的输入输出数据作为训练样本。
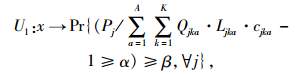
|
(5) |
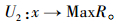
|
(6) |
第2步:利用以上训练样本训练一个BP神经网络以逼近不确定函数U1和U2。
第3步:在d维问题空间上对微粒群进行初始化。设定群体规模为popsize,在决策向量Qjka的可行域中产生一个随机数,归一化后利用神经网络计算网络的仿真输出值并进行反归一化,然后检验该随机数的可行性,即判断Qjka是否满足
第4步:利用训练好的神经网络计算每个归一化后微粒的网络仿真输出值,并进行反归一化,即计算MaxR作为每个微粒的适应值。
第5步:对每一个微粒将其最好适应值与全局所经历的最好适应值进行比较,较好者作为当前的全局最好位置,并再按照式(7)和式(8)对速度和位置进行更新。
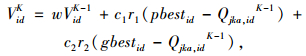
|
(7) |
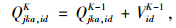
|
(8) |
式中,Vidk为k次迭代后整个种群最优粒子的速度;w为惯性权重因子;c1和c2分别为认知学习因子和社会学习因子;r1和r2都是[0, 1]内均匀分布的随机数;pbestid是每个粒子当前找到的最优粒子位置;gbestid是整个种群当前所找到的最优粒子位置。
第6步:对更新后的微粒再次进行归一化处理,利用神经网络计算网络的仿真输出值并进行反归一化,检验微粒的可行性。若为可行解,则接受,否则保持原位置不变。
第7步:如果完成K次迭代,则输出模型最优值,否则返回第4步。
3 实例分析 3.1 数据准备以浙江省某无车承运人为例,采用本文构建的运力资源组织优化模型对运输车队和运力类型的选择进行仿真模拟。在运输市场上,该无车承运人承运的5家货主企业需要其将4类货物分别运往5个不同的目的地,该无车承运人有7家运输车队可供其选择进行合作完成该项运输业务,每个车队具有多种类型的运力可使用。在原运输市场中,由于运力资源分散、且货主企业对运力进行选择具有随机性和路径依赖性,运力资源的组织往往达不到最优,造成运力资源浪费的问题,现通过无车承运人的模式对运力资源的优化调整以提高其使用效率。根据调查,各企业需运输的货物种类、目的地、运输距离等信息如表 1所示,7家运输车队的运力资源情况如表 2所示。
| 企业 | 货物种类 | 目的地 | ||||
| D1 | D2 | D3 | D4 | D5 | ||
| E1 | a | 24/132 | 15/264 | 36/67 | — | 27/58 |
| b | — | 28/264 | — | 54/158 | 18/58 | |
| c | 34/132 | 69/264 | 17/67 | 85/158 | — | |
| d | 18/132 | 25/264 | 21/67 | 46/158 | 71/58 | |
| E2 | b | 11/94 | — | 21/213 | 34/68 | 45/117 |
| d | 33/94 | 18/173 | 25/213 | — | 55/117 | |
| E3 | a | 41/235 | 32/62 | 19/86 | 24/115 | 34/151 |
| b | — | 19/62 | 57/86 | 34/115 | 29/151 | |
| d | 61/235 | — | 24/86 | 53/115 | 11/151 | |
| E4 | a | — | 52/142 | 24/34 | — | 37/129 |
| b | 21/204 | 67/142 | 31/34 | 46/67 | — | |
| c | 28/204 | 37/142 | 51/34 | 10/67 | 24/129 | |
| E5 | a | 37/53 | 43/121 | — | — | 22/207 |
| b | 16/53 | 27/121 | 41/90 | 22/129 | 74/207 | |
| c | — | 61/121 | 38/90 | 42/129 | 21/207 | |
| 注:a/b分别为运输量和运输距离,单位分别为t和km。 | ||||||
| 车队 | 车型 | |||
| V1 | V2 | V3 | V4 | |
| A | 8/3/(5/7/2/4/8) | 17/10/(5/7/2/4/8) | 25/0/(5/7/2/4/8) | 35/4/(5/7/2/4/8) |
| B | 8/4/(1/5/9/14/11) | 17/5/(1/5/9/14/11) | 25/5/(1/5/9/14/11) | 35/10/(1/5/9/14/11) |
| C | 8/8/(2/9/14/5/7) | 17/0/(2/9/14/5/7) | 25/12/(2/9/14/5/7) | 35/9/(2/9/14/5/7) |
| D | 8/6/(11/7/15/2/4) | 17/14/(11/7/15/2/4) | 25/9/(11/7/15/2/4) | 8/0/(11/7/15/2/4) |
| E | 8/5/(14/2/6/8/4) | 17/9/(14/2/6/8/4 | 25/6/(14/2/6/8/4) | 35/9/(14/2/6/8/4) |
| F | 8/0/(4/9/18/11/7) | 17/12/(4/9/18/11/7) | 25/9/(4/9/18/11/7) | 35/6/(4/9/18/11/7) |
| G | 8/9(5/19/14/7/3) | 17/7/(5/19/14/7/3) | 25/11/(5/19/14/7/3) | 35/5/(5/19/14/7/3) |
| 注:8/3/(5/7/2/4/8)分别为运力的载重、运力数量、车队到企业1的距离、车队到企业2的距离、车队到企业3的距离、车队到企业4的距离、车队到企业5的距离,单位分别为t, veh, km, km, km, km, km。其他项以此类推。 | ||||
由调查所得的不同吨位车型运输费用情况,可以得到单位运输费用函数F(x),单位为t·km,其中x为货运量,单位为t。
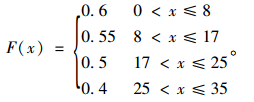
|
(9) |
按照微粒子群和神经网络混合智能算法,设置个参数值为:c1=c2=2,惯性权重w=0.4,最大迭代次数为K=100,训练样本50个,粒子种群规模10,神经元3个,隐形神经元15个,输出神经元3个。根据模型计算,将车队预期利润率设置为5%时,运力资源组织优化的结果如表 3所示。
| 车队 | 车型 | |||
| V1 | V2 | V3 | V4 | |
| A | 2辆:E3aD1(8)+E3dD5(8) | 7辆:E3aD2(32)+E3bD2(19)+E3bD5(29)+E3dD3(17)+E3dD4(17)+E3dD5(3)+E4aD5(2) | — | 4辆:E3aD1(33)+E3bD3(32)+E3dD1(36)+E3dD3(1)+E3dD4(36) |
| B | 4辆:E1aD3(16)+E1aD5(8)+E1dD5(8) | 6辆:E1aD2(15)+E1bD2(2)+E1bD4(19)+E1cD3(17)+E1cD4(15)+E1dD1(17)+E1dD3(17)+E2dD2(1) | 8辆:E1aD1(24)+E1aD3(20)+E1aD5(19)+E1bD2(25)+E1bD5(18)+E1dD2(25)+E1dD3(4)+E2bD5(10)+E2dD5(3)+E3aD3(19)+E3aD4(24)+E3bD3(25)+E3dD3(6) | 9辆:E1bD2(1)+E1bD4(35)+E1cD1(34)+E1cD2(69)+E1cD4(70)+E1dD1(1)+E1dD4(35)+E3aD5(34)+E3bD4(34) |
| C | — | — | 2辆:E1dD5(50) | 5辆:E4aD2(35)+E4aD5(35)+E4bD2(35)+E4bD3(31)+E4cD3(35) |
| D | 2辆:E4bD2(7)+E4cD4(8) | 3辆:E4aD2(17)+E4cD2(17)+E4cD3(16) | 9辆:E4aD3(24)+E4bD1(21)+E4bD2(25)+E4bD4(46)+E4cD1(28)+E4cD2(20)+E4cD4(2)+E4cD5(24)+E5bD4(22)+E5cD3(1) | 3辆:E2bD5(35)+E5bD5(70) |
| E | — | 4辆:E2bD1(11)+E2bD3(17)+E2dD2(17)+E2dD5(17)+E5bD1(3) | 2辆:E2dD3(25)+E3dD1(25) | 3辆:E2bD4(34)+E2dD1(33)+E2dD5(35) |
| F | — | 1辆:E1dD4(11) | — | — |
| G | 6辆:E5aD2(8)+E5bD1(8)+E5bD2(8)+E5bD3(8)+E5bD5(4)+E5cD4(7)+E5cD5(4) | 3辆:E5aD1(17)+E5cD2(17)+E5cD5(17) | 3辆:E5aD1(20)+E5aD5(22)+E5bD1(5)+E5bD2(19)+E5cD2(9) | 5辆:E5aD2(35)+E5bD3(33)+E5cD2(35)+E5cD3(37)+E5cD4(35) |
| 注: E3aD1(8)+E3dD5(8)分别为运输需求企业、货物种类、目的地及货物运输量,单位为t。其他项以此类推。 | ||||
3.3 结果分析
(1) 车队A安排13辆货车,其中2辆V1型货车、7辆V2型货车、4辆V4型货车,运力共计275 t,有效运力使用率为99.3%;车队B安排27辆货车,其中4辆V1型货车、6辆V2型货车、8辆V3型货车、9辆V4型货车,运力共计684 t,有效运力使用率为98.0%;车队C安排7辆货车,其中2辆V3型货车、5辆V4型货车,运力共计225 t,有效运力使用率为98.2%;车队D安排17辆货车,其中2辆V1型货车、3辆V2型货车、9辆V3型货车、3辆V4型货车,运力共计397 t,有效运力使用率为96.5%;车队E安排9辆货车,其中4辆V2型货车、2辆V3型货车、3辆V4型货车,运力共计223 t,有效运力使用率为97.3%;车队F安排1辆V2型货车,运力共计17 t,有效运力使用率为64.7%;车队G安排17辆货车,其中6辆V1型货车、3辆V2型货车、3辆V3型货车、5辆V4型货车,运力共计349 t,有效运力使用率为99.7%。
(2) 无车承运人的利润为11 526.95元,利润率为6.76%。车队A的运输成本为17 547.95元,利润率为5.26%;车队B的运输成本为45 262.4元,利润率为5.52%;车队C的运输成本为8 129.6元,利润率为5.41%;车队D的运输成本为54 527.6元,利润率为5.57%;车队E的运输成本为14 762.8元,利润率为5.16%;车队F的运输成本为955.9元,利润率为5.23%;车队G的运输成本为19 293.3元,利润率为5.45%。
4 结论(1) 无车承运人通过整合货源,并对运力进行合理组织,开展与运输需求企业及运输企业之间的协作,能够提供高质量的运输服务,有效提高运输组织化程度,降低运输车辆空驶率,降低物流成本,可以降低能源消耗,减少污染物排放,对交通运输业节能减排具有重要意义。
(2) 针对无车承运人全程收费、通过合理调度收取运费差价的盈利模式以及与运输需求企业和运输企业之间进行运价谈判的特点,综合考虑运输成本、运输车型等因素,构建了带有机会约束条件无车承运人运力资源优化配置模型。
(3) 案例计算结果分析表明,通过合理组织,7个车队的平均有效运力使用率为93.39%,平均利润率达5.37%,不仅能够保证无车承运人和运输企业利润在一定的可接受范围内,而且能够降低运输成本,对科学组织运力资源,具有重要的应用价值。
(4) 无车承运人的运力资源优化配置受运输价格、供需双方、运输过程等多重因素的影响,在今后的研究中,将考虑运输市场价格波动、运输过程时间窗要求等因素对运力资源配置结果的影响。
| [1] | 董娜. 无车承运人的优势分析和发展建议[J]. 交通标准化 , 2011, 12 (24) : 87-90 DONG Na. Superiority and Advice of Non-Car Operating Carrier[J]. Transportation Standardization , 2011, 12 (24) : 87-90 |
| [2] | 杨传堂.坚持五大发展理念推进结构性改革为全面建成小康社会当好先行[EB/OL]. (2015-12-28)[2016-02-28]. http://www.moc.gov.cn/zhuanti/2016jiaotonggongzuo_HY/201512/t20151228_1966865.html. |
| [3] | RAHIMI-VAHED A, CRAINIC T G, GENDREAU M, et al. A Path Relinking Algorithm for a Multi-Depot Periodic Vehicle Routing Problem[J]. Journal of Heuristics , 2013, 19 (3) : 497-524 |
| [4] | 侯爽.多车场整车任务调度问题研究[D].济南:山东大学, 2012. HOU Shuang. Research on Multi-depot Vehicle Scheduling Problem with Full Car Load[D].Jinan:Shandong University, 2012. |
| [5] | REPOUSSIS P P, TARANTILIS C D. Solving the Fleet Size and Mix Vehicle Routing Problem with Time Windows via Adaptive Memory Programming[J]. Transportation Research Part C:Emerging Technologies , 2010, 18 (5) : 695-712 |
| [6] | SUBRAMANIAN A, PENNA P H V, UCHOA E, et al. A Hybrid Algorithm for the Heterogeneous Fleet Vehicle Routing Problem[J]. European Journal of Operational Research , 2012, 221 (2) : 285-295 |
| [7] | HUTH T, MATTFELD D C. Integration of Vehicle Routing and Resource Allocation in a Dynamic Logistics Network[J]. Transportation Research Part C:Emerging Technologies , 2009, 17 (2) : 149-162 |
| [8] | LIN Zi-kui, CHEN Lei. Notice of Retraction Multi-target Optimization Model of Logistics Resources Allocation[C]//2009 International Conference on Machine Learning & Cybernetics. Washington, D.C.:IEEE, 2009:2587-2592. |
| [9] | 胡青蜜, 胡志华, 陶莎. 二级轴辐式零担物流网络设计的资源均衡利用问题[J]. 公路交通科技 , 2013, 30 (4) : 124-131 HU Qin-mi, HU Zhi-hua, TAO Sha. Resource Balanced Usage Problem for Bi-level Hub-and-spoke LTL Logistics Network Design[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (4) : 124-131 |
| [10] | 房巧红, 陈功玉. 再制造逆向物流网络的机会约束目标规划模型[J]. 工业工程与管理 , 2010, 15 (1) : 74-81 FANG Qiao-hong, CHEN Gong-yu. Chance-constrained Goal Programming Model for Remanufacturing Reverse Logistics Network[J]. Industrial Engineering and Management , 2010, 15 (1) : 74-81 |
| [11] | 邵增珍.物流匹配问题的调度模型和算法研究[D].济南:山东师范大学, 2013. SHAO Zeng-zhen. Research on Scheduling Model and Algorithms of Logistics Matching Problem[D].Jinan:Shandong Normal University, 2013. http://www.cnki.com.cn/article/cjfdtotal-jfyz201311009.htm |
| [12] | 王旭, 田帅辉, 王振锋. 面向物流任务的跨组织边界物流资源优化配置[J]. 计算机集成制造系统 , 2012, 18 (2) : 389-395 WANG Xu, TIAN Shuai-hui, WANG Zhen-feng. Inter-organizational Boundaries' Logistics Resource Optimized Allocation Oriented to Logistics Task[J]. Computer Integrated Manufacturing Systems , 2012, 18 (2) : 389-395 |
| [13] | 肖宁. 求解随机机会约束规划的混合智能算法[J]. 计算机工程与应用 , 2010, 46 (22) : 43-46 XIAO Ning. Solving Stochastic Chance-constrained Programming Problems with Hybrid Intelligent Algorithm[J]. Computer Engineering and Applications , 2010, 46 (22) : 43-46 |
| [14] | HONG S P, KIM Y H. A Genetic Algorithm for Joint Replenishment Based on the Exact Inventory Cost[J]. Computers Operations Research , 2009, 36 (1) : 167-175 |
| [15] | 刘志雄, 梁华. 粒子群算法中随机数参数的设置与实验分析[J]. 控制理论与应用 , 2010, 27 (11) : 1489-1496 LIU Zhi-xiong, LIANG Hua. Parameter Setting and Experimental Analysis of the Random Number in Particle Swarm Optimization Algorithm[J]. Control Theory & Applications , 2010, 27 (11) : 1489-1496 |
 2016, Vol. 33
2016, Vol. 33
