扩展功能
文章信息
- 彭怀军, 秦勇, 张尊栋, 杨艳芳
- PENG Huai-jun, QIN Yong, ZHANG Zun-dong, YANG Yan-fang
- 基于遗传算法的二元覆盖模型在交通警力部署中的应用
- Application of Dual Coverage Model Based on Genetic Algorithm in Traffic Police Deployment
- 公路交通科技, 2016, 33(10): 125-130
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 125-130
- 10.3969/j.issn.1002-0268.2016.10.019
-
文章历史
- 收稿日期: 2015-09-10
2. 北方工业大学 城市道路交通智能控制技术北京市重点实验室, 北京 100144
2. Beijing Key Lab of Urban Intelligent Traffic Control Technology, North China University of Technology, Beijing 100144, China
在交通日益拥堵的城市里,维护交通秩序、疏导拥堵交通路段、快速处理交通事故是交警日常勤务管理工作中的重要工作[1]。然而基层交通警力不足是我国交通管理部门面临的普遍问题,如何在有限的警力条件下科学合理地配置警力、快速有效地调度警力一直是我国各级交通管理部门探索的问题[2-3]。交通警力优化部署问题是交通管理中交警勤务管理工作的难点,现有国内外研究中针对交通警力资源部署的模型和算法成果并不多见。
出警时间是衡量城市交警响应快慢的主要指标,很多城市交管部门向公众公布了最快出警时间。在最小的警力资源配置下,合理部署警力和划分责任范围才能保障区域内出警时间能达到相关的规定,提高公众服务满意度。将出警时间作为依据进行警力部署,可以应用经典的二元覆盖模型解决交通警力部署问题。集合覆盖模型(Set Covering Location Model, SCLM)和最大覆盖模型(Maximum Covering Location Model, MCLM)是两类基本覆盖模型[4],其覆盖函数是二元化的,因此属于二元覆盖模型[5-6]。根据警力资源是否有最大数量限制,可将交通警力部署问题分成无资源限制和资源受限的两类警力部署问题,本文应用SCLM和MCLM来解决这两类问题。
常见的优化算法中,单纯形法、梯度法、分枝定界法等属于确定性的优化算法,目的是求得全局最优解,但受计算效率的影响,对大规模优化问题明显不足。遗传算法具有鲁棒性强、简单易行、计算速度快、可求出较好质量近似解的特点,被不少专家应用在求解SCLM和MCLM中[7-11]。
本文在介绍SCLM和MCLM在交通警力部署问题中的应用后,分析了最大覆盖模型应用的限定条件,然后应用遗传算法求解两种模型,并应用北京市交通警力部署案例进行实例验证。
1 应用于交通警力部署的二元覆盖模型 1.1 模型参数说明在交通警力部署问题中,将城市路网定义为网络空间N(C, R),C和R分别为N的节点(路口)集合和边(路段)集合,路口节点数记为m=|C|。设P为可部署交通警力地点的集合,本文中警力部署地点只可在任意一个路口上,因此有P=C。定义Dc为警力在规定出警时间内能达到的覆盖距离,dij为路口i到可部署警力的地点j之间的最短距离(∀i∈C, ∀j∈P)。
模型用到的变量定义如下:

|
wi为路口i的警力需求量或权重(如路口交通事件量、路口等级等);
p为可部署的最大警力数量。
1.2 模型假设为了简化计算分析,模型应用中提出以下假设:
(1) 将出警时间作为警力部署的依据,忽略交通事故分布、工作量等其他影响因素。
(2) 假定需要出警需求点和警力部署地点都只在路口上。
(3) 不考虑区域特点、重点保障道路等情况,假设所有地区出警时间要求一致。
(4) 假设出警速度一致,不考虑道路条件和不同时段实际交通拥堵状态的影响。
(5) 只考虑主干道,忽略次干道和低级别道路。
(6) 假定覆盖函数是限定0-1变量的二元化的函数,需求要么被覆盖,要么不被覆盖。当dij≤DC时,则认为路口i被地点j部署的警力覆盖;dij>DC时,则路口i不被地点j部署的警力覆盖。
1.3 集合覆盖模型SCLM最早由Roth[12]和Toregas [13]提出,用于解决应急型公共服务设施选址问题。无资源限制的警力部署问题实际是一种集合覆盖问题,是寻找最小警力资源部署点的集合,使得每个路口节点至少被1个警力在规定的出警时间内覆盖。解决这一问题的SCLM可以表示为:
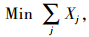
|
(1) |
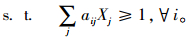
|
(2) |
目标函数(1)是要找到最佳的警力部署集合使得部署的警力总数最少;约束条件(2)表示每个路口都能被至少1个警力所覆盖。
1.4 最大覆盖模型MCLM最早由Church和Velle在1974年提出[14]。资源受限的警力部署问题实际是一种最大覆盖问题,是在有限的警力资源下如何进行警力部署,使得在规定的出警时间内覆盖尽可能多的路口。解决这一问题的MCLM可以表示为:
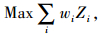
|
(3) |
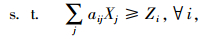
|
(4) |
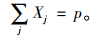
|
(5) |
目标函数(3)是要找到1个警力部署集合使得路口总覆盖量最大,不考虑需求量或权重时,wi=1。约束条件(4)表示如果某路口被覆盖,该路口至少需要被1个警力所覆盖,其中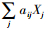
在MCLM中限定了可部署的最大警力数量p,接下来研究p的约束条件。
假设p是递增变量,当p增加到一定值p′,可使得所有需求点都被覆盖。此时,在∀i条件下,都有Zi=1,目标函数(3)为固定值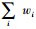
由于当p≥p′时,Zi=1,则约束条件(4)与SCLM的约束条件(2)一致。由于假定p是变量,约束条件(5)与SCLM目标函数(1)一致。可见,p′是使所有需求点都被覆盖的最小设施数量,这正是SCLM求的结果:
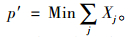
|
(6) |
在交通警力部署应用中,应将SCLM求得的全覆盖最小警力资源数与可部署的警力数量相比较,如果可部署的警力数量较少,可以应用MCLM求解,否则需应用SCLM求得的结果。
2 应用遗传算法求解模型 2.1 遗传算法介绍遗传算法(Genetic Algorithm,GA)是模拟生物进化过程的随机搜索优化算法,最早由J.Holland教授于1975年提出[15]。GA将问题的变量编码为染色体,再利用选择、交叉和变异3个基本算子进行运算来交换染色体信息,生成符合优化目标的染色体,再进行解码得到优化结果[16]。GA基本运算流程如图 1所示,具体过程如下:

|
| 图 1 遗传算法流程图 Fig. 1 Flowchart of genetic algorithm |
| |
(1) 染色体编码:根据问题对变量进行编码,设定染色体长度;
(2) 种群初始化:设置进化代数计数器g=0,随机生成设定的M个个体作为初始种群Pg=0;
(3) 适应度计算:对种群Pg中各个体进行解码,并根据适应度函数F(x)计算的每个个体的适应度;
(4) 选择运算:根据选择概率ps和各个体的适应度,通过选择算子选取优良个体进行下一代繁衍,实现基因的优胜劣汰;
(5) 交叉运算:根据交叉概率pc对种群两两个体进行基因交换,形成新个体;
(6) 变异运算:对新个体以一定的变异概率pm进行基因值的变异操作,最终生成下一代种群Pg+1;
(7) 终止条件判断:根据遗传代数或适应度提升情况判断是否满足条件,如果满足条件,则终止计算,以进化过程中具有最大适应度的个体作为最优解输出,否则跳转到步骤(3)进行下一代运算。
2.2 GA算法实现的关键问题决策变量的编解码、适应度函数的设计和约束条件的处理是SCLM和MCLM优化算法实现的关键问题。下面从这3个角度阐述GA实现中的处理方法。
(1) 决策变量的编解码
编解码是为了便于算法的计算机编程处理而进行的信息格式转换,为了编程计算方便,一般将编码设计成长二进制的形式。编解码的设计影响到最优解搜索和解码计算效率,对算法的收敛性和运行效率有很大影响。在GA中,要将问题的变量编码为染色体,在计算适应度和输出最优解时进行解码处理。
在SCLM和MCLM中,决策变量Xj和Zi均为0-1变量,每种决策变量的数量为路口节点数量m,将所有变量组成一个长二进制,直接用于算法流程中。
(2) 适应度函数的设计
适应度函数也称评价函数,在GA迭代过程中,用其求得可行解的适应度作为可行解的择优指标,通过优胜劣汰寻找最优解。适应度函数在迭代过程中调用,计算越简单越能提升算法总体效率。由于在选择运算过程中要进行个体比较排序,适应度函数要具有单调一致、非负、最大化和计算量小的特点。
在本文的算法实现中,SCLM的适应度函数为: 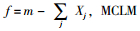
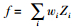
(3) 约束条件的处理
约束条件的处理是优化算法研究的热点内容,也是处理实际问题经常遇到的难题,目前还没有适合各类约束的普适性方法。在应用中,常用处理约束条件的方法有限定搜索方向法、改变迭代算法、可行解变换法、罚函数法。其中,前3种算法常处理一些简单的约束条件,罚函数法则是应用最广的一种方法。在罚函数法中, 罚函数及惩罚因子设计是难点,既要体现出不可行解对约束条件的不满足程度而加快算法收敛,又具有较高的计算效率。
在本文GA的算法实现中,SCLM的约束条件(2)采用罚函数法进行处理,算法迭代过程中,不满足约束条件的个体通过惩罚因子淘汰。而在MCLM中有两个约束条件(4)和(5),很难设计两个条件不满足程度的罚函数,同时用两个罚函数处理时出现不能收敛的现象,因此需要进行算法改进。
2.3 求解MCLM的GA算法改进求解MCLM的GA算法实现中,由于难以处理两个约束条件,本文研究中对算法进行了优化改进。
虽然MCLM中决策变量Xj与SCLM相同,但根据约束条件(5),实际Xj只有组合数Cmp个可行解。为了提高编解码效率,本文结合约束条件(5)对Xj用自然二进制码进行编码,每个节点的二进制编码长度为log2m向上舍入取整,决策变量Xj总编码为长度p×log2m。解码时,需要将大于m的编码减去一个值映射成有效的路口节点编号,通过增加部分解的搜索频次减少无效解的约束条件处理,从而提高算法效率。
MCLM的约束条件(4)在实现中处理方法比较特殊,决策变量Zi是结合定义与目标函数(3)由决策变量Xj的值计算出来的。模型中,通过Xj可求出覆盖次数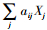
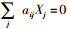
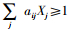
算法实现中,用约束条件(4)和决策变量Xj计算出Zi,既减少了编码长度,也处理了约束条件,大大提升了算法效率。
3 实例分析 3.1 试验环境及数据说明为了验证算法的有效性,本文应用Matlab 2014a编程实现GA算法,并在CPU Intel Xeon E5-2643 3.30 GHz、内存64 G的Win Server 2008 R2 64位操作系统上运行。
试验数据是北京市海淀区和西城区二环到四环的主要路口和道路(包含成府路和学院路部分路口)的路网数据,数据中包含106个路口节点,181条边(边长为实际道路长度)。这部分路网属于城市道路的核心区域,路口分布比较均匀,没有特别长的路段,比较适合只按照到达时间的单一条件进行警力部署。
试验中假定路口发生事故后交警要在规定3 min内到达。根据北京市交通道路的平均交通状况,假定交警车辆行驶速度为30 km/h,则交警有效的覆盖半径为1.5 km。为简化模型计算,假定事故发生和警力部署位置都按照路口来计算,因此本试验中的需求和部署点是所有的路口节点。
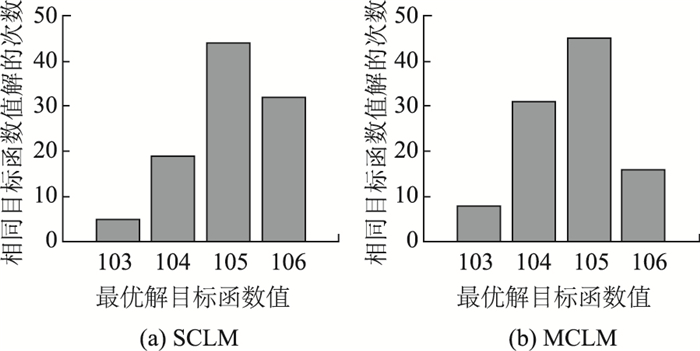
3.2 试验结果与分析由于GA每次计算结果不完全一致,试验中,对SCLM和MCLM(限定警力资源数p=17)的算法各运行100次,记录每次运行结果的目标函数值,形成两种模型的运行结果统计图,如图 2所示。
|
| 图 2 SCLM和MCLM的运行结果统计图 Fig. 2 Statistical operation results of SCLM and MCLM |
| |
由图 2可以看出:
(1) SCLM的最优解目标函数为17,MCLM(p=17)的最优解目标函数为106;
(2) GA求得的解不是唯一的,可见GA求解具有不稳定性;
(3) GA求得的所有解接近最优解。
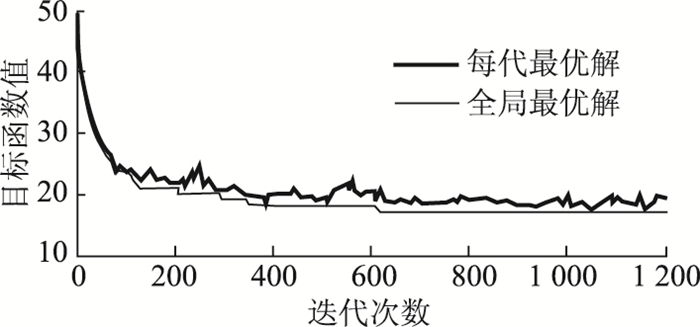
将每次迭代过程中的最优目标函数值记录下来绘制成迭代进程图,如图 3和图 4所示。
|
| 图 3 SCLM的迭代进程图 Fig. 3 Iterative process of SCLM |
| |
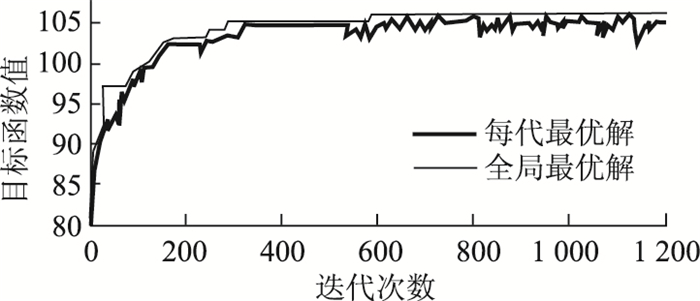
|
| 图 4 MCLM(p=17)的迭代进程图 Fig. 4 Iterative process of MCLM (p=17) |
| |
将SCLM与MCLM(p=17)计算最优结果按照选址路口和覆盖路口范围进行对比,如表 1所示。
| 集合覆盖模型 | 最大覆盖模型 | ||
| 选址路口 | 覆盖路口 | 选址路口 | 覆盖路口 |
| 17 | 16, 17, 18, 19, 49, 52, 56, 60, 90, 91, 93 | 60 | 17, 18, 19, 49, 50, 52, 53, 56, 57, 60, 61, 64, 65 |
| 22 | 22, 23, 78, 99, 101 | 22 | 22, 23, 78, 79, 99 |
| 31 | 30, 31, 32, 33 | 31 | 30, 31, 32, 33 |
| 34 | 34, 35, 92, 94 | 92 | 34, 35, 90, 91, 92, 93, 94 |
| 38 | 1, 2, 8, 9, 37, 38, 39 | 38 | 1, 2, 8, 9, 37, 38 |
| 41 | 11, 40, 41, 44, 46, 47 | 40 | 10, 11, 39, 40, 41, 44, 46, 47 |
| 42 | 13, 14, 42, 43, 45 | 42 | 12, 13, 14, 42, 43, 45 |
| 58 | 3, 4, 5, 48, 50, 5153, 54, 55, 57, 58, 59, 61, 62, 63, 65, 66, 67 | 59 | 3, 4, 5, 48, 51, 5455, 58, 59, 62, 63, 66, 67 |
| 71 | 20, 21, 64, 71, 72, 74, 75 | 21 | 20, 21, 71, 74 |
| 77 | 6, 7, 68, 69, 70, 73, 76, 77 | 77 | 6, 7, 68, 69, 70, 72, 73, 75, 76, 77 |
| 80 | 10, 24, 79, 80 | 24 | 24, 80, 102 |
| 82 | 12, 26, 81, 82 | 25 | 25, 26, 81 |
| 84 | 27, 28, 29, 83, 84, 85 | 84 | 27, 28, 29, 82, 83, 84, 85 |
| 88 | 15, 86, 87, 88, 89 | 88 | 15, 16, 86, 87, 88, 89 |
| 96 | 36, 95, 96, 97, 98 | 98 | 36, 95, 96, 97, 98 |
| 103 | 100, 102, 103 | 100 | 100, 101, 103 |
从表 1可以看出,选址路口有8个是重合的,其余基本上是相近的,每个路口覆盖的范围也都近似,可见两模型求得结果是相近的。
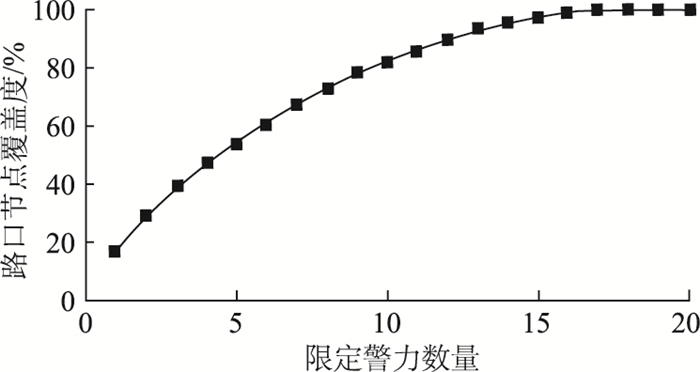
将限定警力资源数p从1一直到20改变,重复计算MCLM最优的覆盖结果,得到路口节点覆盖度与限定警力资源数量的关系,如图 5所示。
|
| 图 5 MCLM限定警力数量与覆盖度的关系 Fig. 5 Relationship between limited number of police and coverage in MCLM |
| |
可以看出,随着限定警力资源数量的增大,覆盖度增大趋势变缓,当限定警力资源数量大于等于17时,覆盖度达到最大值100%。前面试验结果中,SCLM求得的最优解为17个路口节点,这正是MCLM中覆盖度达到100%的限定警力资源数量临界值。这说明试验结果与式(6)结果是一致的。
4 结论本文应用二元覆盖的两类基本覆盖模型SCLM和MCLM来解决无资源限制和资源受限的两类交通警力部署问题,并采用遗传算法对两种覆盖模型进行了求解。以北京部分路网数据对模型的算法进行了验证和分析。根据试验结果,GA求解具有不稳定性,每次求得的解与最优解可能存在一定的偏差,但这种偏差是有限的。
试验结果表明,MCLM的限定警力数量不是任意大,不能大于SCLM求得的最小警力数量。在资源受限的交通警力部署应用中,应先用SCLM求出全覆盖下的最小警力资源数。再与限定的警力数量进行对比,如果限定的警力数量较少,则应用MCLM求解;如果限定的警力数量大,则直接应用SCLM求解结果,不必部署所有的警力。
| [1] | 张准民, 周云金, 王时杰, 等. 探索和建立交通管理"责任区"勤务模式[J]. 上海公安高等专科学校学报 , 2002, 12 (5) : 51-52 ZHANG Zhun-min, ZHOU Yun-jin, WANG Shi-jie, et al. Probe into and Establish the "Responsibility Area" Duty Model of Traffic Administration[J]. Journal of Shanghai Public Security Academy , 2002, 12 (5) : 51-52 |
| [2] | 张湛. 北京市高峰勤务机制实施效果分析[J]. 道路交通与安全 , 2010, 10 (5) : 46-48 ZHANG Zhan. The Evaluation of "Rush Hour Traffic Policing Mode"[J]. Road Traffic & Safety , 2010, 10 (5) : 46-48 |
| [3] | 张兵. 高峰交通勤务工作的实践探索与理性思考[J]. 公安研究 , 2014 (4) : 26-30 ZHANG Bing. Practice Exploration and Rational Thinking of Peak Traffic Service WOrk[J]. Policing Studies , 2014 (4) : 26-30 |
| [4] | DASKIN M. Network and Discrete Location:Models, Algorithms and Applications[J]. Journal of the Operational Research Society , 1996, 48 (7) : 763 |
| [5] | BERMAN O, KRASS D, DREZNER Z. The Gradual Covering Decay Location Problem on a Network[J]. European Journal of Operational Research , 2003, 151 (3) : 474-480 |
| [6] | 张宗祥, 杨超, 陈中武. 基于服务质量的多目标逐渐覆盖问题研究[J]. 公路交通科技 , 2013, 30 (10) : 92-97 ZHANG Zong-xiang, YANG Chao, CHEN Zhong-wu. Multi-objective Gradual Covering Problem Based on Service Quality[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (10) : 92-97 |
| [7] | BEASLEY J E. An Algorithm for Set Covering Problem[J]. European Journal of Operational Research , 1987, 31 (19) : 85-93 |
| [8] | BEASLEY J E, CHU P C. A Genetic Algorithm for the Set Covering Problem[J]. European Journal of Operational Research , 1994, 94 (2) : 392-404 |
| [9] | GROSSMAN T, WOOL A. Computational Experience with Approximation Algorithms for the Set Covering Problem[J]. European Journal of Operational Research , 1997, 101 (1) : 81-92 |
| [10] | BERMAN O, KRASS D. The Generalized Maximal Covering Location Problem[J]. Computers & Operations Research , 2002, 29 (6) : 563-581 |
| [11] | AYTUG H, SAYDAM C. Solving Large-scale Maximum Expected Covering Location Problems by Genetic Algorithms:A Comparative Study[J]. European Journal of Operational Research , 2002, 141 (3) : 480-494 |
| [12] | ROTH R. Computer Solutions to Minimum-cover Problems[J]. Operations Research , 1969, 17 (3) : 455-465 |
| [13] | TOREGAS C, SWAIN R, REVELLE C, et al. The Location of Emergency Service Facilities[J]. Operations Research , 1971, 19 (2) : 93-95 |
| [14] | RICHARD C, VELLE C R. The Maximal Covering Location Problem[J]. Papers in Regional Science , 1974, 32 (1) : 101-118 |
| [15] | HOLLAND J H. Adaptation in Nature and Artificial Systems[M]. Ann Arbor: University of Michigan Press, 1975 . |
| [16] | 於昊, 陈峻, 王炜, 等. 基于遗传算法的停车设施选址规划[J]. 公路交通科技 , 2000, 17 (6) : 53-55 YU Hao, CHEN Jun, WANG Wei, et al. Genetic Algorithm Based Method for Parking Facility Planning[J]. Journal of Highway and Transportation Research and Development , 2000, 17 (6) : 53-55 |
 2016, Vol. 33
2016, Vol. 33
