扩展功能
文章信息
- 陈娇娜, 张生瑞, 靳引利
- CHEN Jiao-na, ZHANG Sheng-rui, JIN Yin-li
- 高速公路行程时间可靠性模型参数估计方法比较分析
- Comparative Analysis of Parameter Evaluation Methods for Expressway Travel Time Reliability Model
- 公路交通科技, 2016, 33(10): 118-124
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 118-124
- 10.3969/j.issn.1002-0268.2016.10.018
-
文章历史
- 收稿日期: 2015-11-26
2. 长安大学 电子与控制工程学院, 陕西 西安 710064
2. School of Electrical and Control Engineering, Chang'an University, Xi'an Shaanxi 710064, China
高速公路行程时间可靠性是指在高速公路上给定的起终点之间,出行者能在规定时间内顺利完成出行的概率[1]。高速公路行程时间可靠性能有效地衡量高速公路路网的不确定性,是微观出行决策的重要考虑因素和评价出行服务水平及道路运行效率的关键指标[2]。
柏喜红等[3]从路、人、环境和技术4个方面分析了高速公路行程时间可靠性的影响因素,并总结了数理统计、缓冲时间、行程延误、行程时间分布宽度和斜度4个角度的评价指标及适用性。降雨[4-5]、雾天[6]、冰雪[7]、交通事故[8]等条件下对行程时间可靠性影响的研究相继开展。Bell等[9]认为,当交通量较大时,路径行程时间服从正态分布,当交通量不大时,服从对数正态分布。Arezoumandi[10]分析了伽马分布、最大极值分布、log-logistic概率分布、对数正态分布及威布尔分布与18 h行程时间数据的拟合程度,认为可变限速情形下行程时间的分布服从对数正态分布。陈琨等[11]使用北京市浮动车数据,分别用正态分布、对数正态分布、伽马分布和威布尔分布对路段行程时间的概率密度函数进行了曲线拟合,结果表明对数正态分布的拟合效果最佳。尹志鹏[12]基于对数正态分布,采用标准差、缓冲指数和拥挤频率来评价旅行时间可靠性。浮动车数据[13]、车检器数据[14]和收费数据[15]被应用于高速公路路段行程时间预测研究。
虽然在行程时间分布模型方面的研究不断深入,但尚未涉及模型参数估计方法对评价结果的影响。Zhou[16]和Taraldsen[17]介绍了对数正态分布的常见估计方法。于洋[18]认为对于同一组样本观测值,采用不同估计方法得到的对数正态分布参数估计值是不同的。由于不同参数标定方法的差异,如何选取符合可靠性评价适用条件的参数估计方法已成为亟待解决的问题。
本文分别对客车和货车的行程时间分布进行拟合,验证高速公路行程时间的分布模型,并比较最大似然参数估计和最小二乘参数估计的拟合效果;建立高速公路行程时间可靠性模型,结合4类可靠性评价指标特征,提出一种确定可接受的行程时间阈值的方法;最后,通过实际高速公路收费数据验证模型的适用性。
1 高速公路行程时间可靠性由文献[11]可知,路段行程时间的概率密度函数可以由对数正态分布模型来描述。对数正态分布的概率密度函数如下:
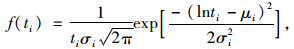
|
(1) |
式中,ti为路段的行程时间;μi和σi分别为路段行程时间的期望和标准差。
路段i的行程时间可靠性模型可以描述为:
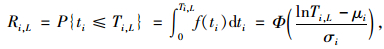
|
(2) |
式中,Ri, L为在服务水平L下路段i行程时间可靠度;ti为路段i的实际行程时间;Ti, L为在服务水平L下路段i行程时间的阈值。从道路管理者角度出发,Ti, L是一个固定值;从道路使用者角度出发,时间阈值Ti, L是一个随机变量。
从上述定义可知,求解路段行程时间可靠性的问题,实际上就是求解路段行程时间的累计分布函数。
2 模型参数估计方法比较 2.1 数据预处理高速公路收费数据包含了出/入口站编号、出/入口时间、车型/车种等信息[19],忽略收费站所产生的延误,车辆的行程时间为记录的出站时间与入站时间之差。由于系统故障、人工误操作、特殊驾驶行为等因素,可能会产生异常或错误数据。因此,剔除异常数据后,根据统计原理选取t±2σ范围内数据为有效样本数据,t和σ为样本的均值和标准差。
考虑高速公路客车与货车限速值的差异,分为客车和货车两类,选取路网中样本数据量较多的区间作为样本数据集合。样本区间及其分布特征分析如表 1所示。
| 样本 | 区间 | 距离/km | 车型 | 样本数 | 偏度系数 | 峰度系数 |
| T1 | 机场-马家堡-北环路-汉城 | 21.08 | 客车 | 257 648 | 2.061 4 | 5.916 0 |
| T2 | 曲江-长安-高新区 | 10.5 | 124 102 | 3.066 5 | 11.443 6 | |
| T3 | 临潼西-豁口-灞桥 | 16.83 | 45 721 | 2.143 1 | 6.411 2 | |
| T4 | 高新区-长安-曲江 | 10.5 | 112 766 | 3.368 6 | 13.589 4 | |
| T5 | 府谷-石马 | 11.21 | 货车 | 137 717 | 2.036 6 | 5.890 0 |
| T6 | 曲江-曲江立交-长安-高新区-河池寨 | 19.50 | 16 180 | 2.502 4 | 8.350 0 | |
| T7 | 府谷-府谷互通-石马-永兴-神木北-神木 | 57.41 | 16 689 | 2.803 6 | 10.520 0 | |
| T8 | 府谷-府谷互通-石马-永兴 | 38.41 | 18 059 | 3.201 5 | 12.980 0 |
2.2 拟合评价指标
采用误差平方和(SSE)、累积分布函数的误差平方和(SSE of CDF)、确定系数(R2)、偏度系数的相对误差(RES)和峰度系数的相对误差(REK)5个指标来衡量。SSE与SSE of CDF用于反映拟合估计值与样本的接近程度;R2,RES,REK用于说明曲线拟合在解释数据的变异性方面是否成功,样本的分布特征是否得到保留。
SSE为拟合数据和原始数据对应点误差的平方和。SSE of CDF为拟合数据的累积分布函数和原始数据的经验累积分布函数对应点的误差平方和。SSE和SSE of CDF越接近0,则曲线的拟合效果越好。
确定系数R2取值范围为[0, 1],值越接近1,曲线拟合的效果越好。计算如下:
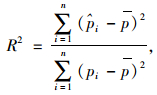
|
(3) |
式中,pi为原始数据中行程时间ti的经验概率值;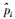
偏度系数的相对误差(RES)和峰度系数的相对误差(REK)计算公式为:
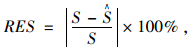
|
(4) |
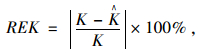
|
(5) |
式中,S和K分别为原始数据的偏度系数和峰度系数;Ŝ和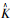
对于容量为n的样本,偏度系数和峰度系数计算公式为:
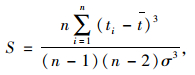
|
(6) |
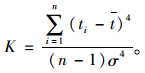
|
(7) |
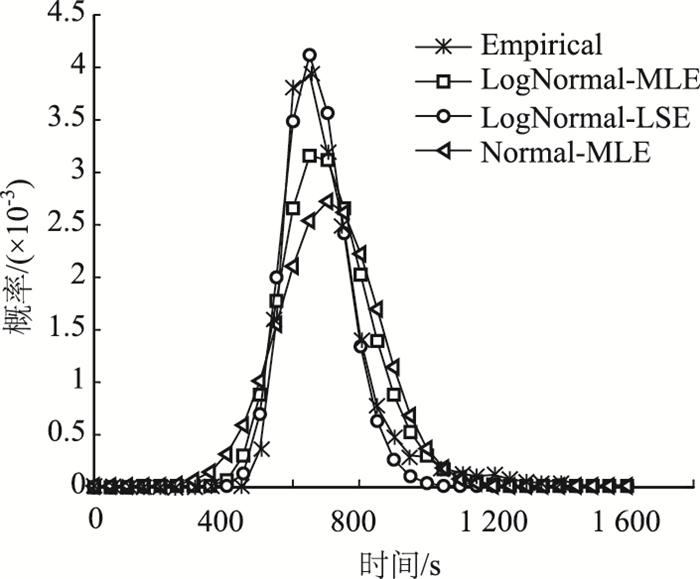
本文采用正态分布和对数正态分布对样本数据进行拟合,比较不同分布以及参数估计方法与实际样本数据的近似程度。其中,正态分布的参数采用最大似然估计,对数正态分布的参数分别采用最小二乘估计和最大似然估计。由于篇幅所限,仅给出样本T1和T5行程时间概率分布及其累积分布曲线的实际值和拟合值比较图,如图 1~图 4所示。样本T1~T8的行程时间分布拟合评价指标结果如表 2所示。
|
| 图 1 T1的行程时间概率分布拟合结果 Fig. 1 Fitting result of travel time probability distribution of T1 注:Empirical为样本经验值;LogNormal-MLE为最大似然估计对数正态分布;LogNormal-LSE为最小二乘估计对数正态分布;Normal-MLE为最大似然估计正态分布,下同。 |
| |
|
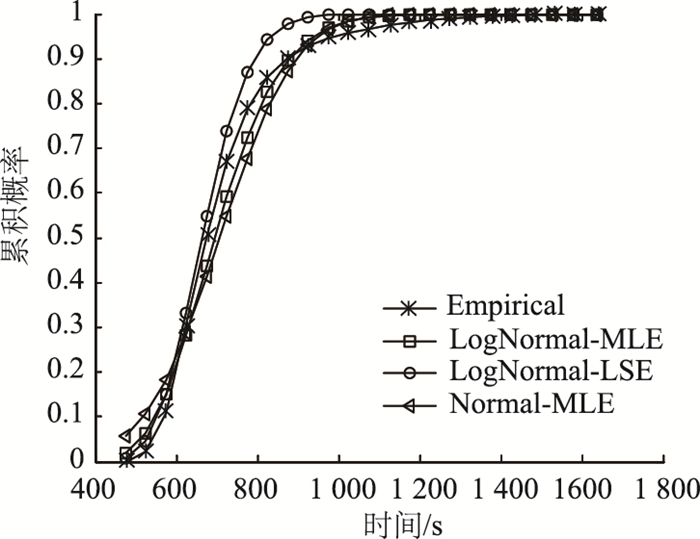
| 图 2 T1的行程时间累积分布拟合结果 Fig. 2 Fitting result of travel time cumulative distribution of T1 |
| |
|
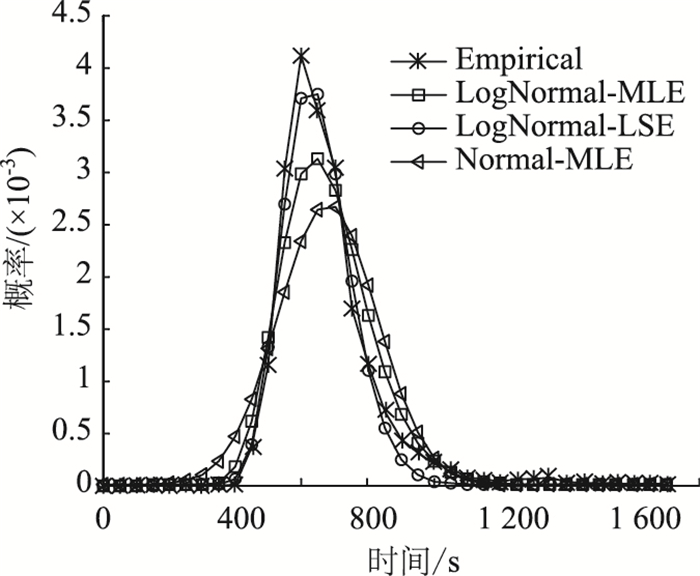
| 图 3 T5的行程时间概率分布拟合结果 Fig. 3 Fitting result of travel time probability distribution of T5 |
| |
|
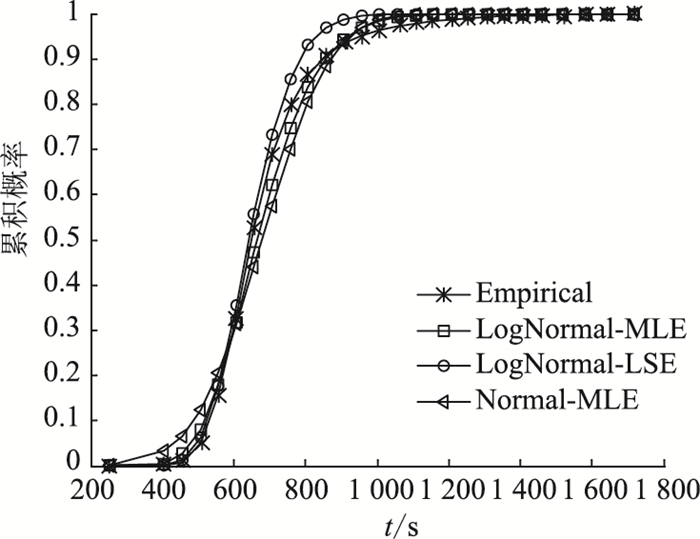
| 图 4 T5的行程时间累积分布拟合结果 Fig. 4 Fitting result of travel time cumulative distribution of T5 |
| |
| 样本 | 104×SSE | R |
SSE of CDF | RES/% | REK/% | ||||||||||
| Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅲ | |
| T1 | 2.02 | 0.46 | 4.62 | 0.81 | 0.98 | 0.70 | 1.14 | 2.04 | 2.96 | 26.10 | 2.11 | 38.03 | 100.97 | 11.83 | 136.41 |
| T2 | 3.17 | 0.44 | 7.79 | 0.76 | 0.99 | 0.61 | 1.17 | 1.34 | 3.64 | 24.14 | 1.15 | 36.98 | 141.79 | 11.62 | 200.04 |
| T3 | 4.34 | 0.51 | 8.02 | 0.66 | 0.98 | 0.52 | 4.70 | 8.61 | 10.70 | 52.94 | 4.48 | 70.28 | 182.93 | 28.63 | 212.31 |
| T4 | 3.90 | 0.50 | 10.16 | 0.72 | 0.99 | 0.51 | 1.72 | 2.28 | 6.62 | 28.30 | 1.17 | 45.98 | 179.28 | 14.54 | 259.04 |
| T5 | 1.13 | 0.21 | 3.30 | 0.85 | 0.99 | 0.74 | 0.71 | 1.16 | 2.40 | 22.84 | 2.89 | 34.75 | 93.28 | 18.99 | 130.05 |
| T6 | 1.11 | 0.65 | 2.16 | 0.85 | 0.97 | 0.76 | 0.55 | 0.71 | 1.88 | 19.58 | 5.77 | 27.26 | 107.70 | 44.04 | 139.09 |
| T7 | 1.16 | 0.62 | 1.81 | 0.71 | 0.92 | 0.60 | 5.56 | 5.53 | 14.37 | 35.41 | 10.44 | 45.04 | 202.61 | 88.85 | 236.92 |
| T8 | 1.40 | 0.59 | 2.86 | 0.70 | 0.94 | 0.53 | 4.86 | 3.33 | 17.03 | 31.01 | 7.54 | 45.70 | 201.41 | 73.23 | 263.05 |
| 注:Ⅰ为最大似然估计对数正态分布;Ⅱ为最小二乘估计对数正态分布;Ⅲ为最大似然估计正态分布。 | |||||||||||||||
由表 2中Ⅰ和Ⅲ拟合结果可得,Ⅰ的SSE和SSE of CDF较Ⅲ小,且R2更接近于1。即对数正态分布相比于正态分布具有更好的拟合效果,与文献[11]结论一致。比较Ⅰ和Ⅱ的SSE可知,Ⅱ的SSE小于Ⅰ,说明采用最小二乘参数估计的对数正态分布与经验统计分布误差最小。Ⅰ的SSE of CDF小于或接近Ⅱ,说明采用最大似然估计的对数正态分布能较好地拟合行程时间概率的累积分布。比较Ⅰ和Ⅱ的R2可知,Ⅱ的R2最接近于1,且RES和REK指标最小,说明采用最小二乘估计的对数正态分布能更好地拟合分布的偏态性和峰值。
综上所述,采用相同的参数估计方法时,相比于正态分布,对数正态分布拟合高速公路行程时间效果更优。同时,最小二乘参数估计的对数正态分布能更好地拟合行程时间分布的偏态性和峰值;采用最大似然估计的对数正态分布在拟合行程时间累积概率分布时效果较优。因此,根据行程时间可靠性的定义,为尽量减小参数估计方法引起的误差,在计算可靠度时应使用最大似然参数估计;在进行基于最大可能准则行程时间预测时应使用最小二乘参数估计。
3 高速公路时间可靠性模型建立采用陕西省2015年1月~6月高速公路收费数据作为基础数据,分析路网中不同出行距离和不同出发时段的行程时间可靠性。参考文献[3],选取变异系数(Coefficient of Variable,CV)、缓冲指数(Buffer Index, BI)、行程时间可靠度(Travel Time Reliability,TTR)、遭遇指数(Misery Index,MI)和不可靠性指数(Unreliability Index,UI)作为不同角度评价高速公路行程时间可靠性的指标。
指标计算方法如下:
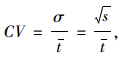
|
(8) |
式中,σ和s分别为标准差和方差;t为某时段内路段上的平均行程时间。
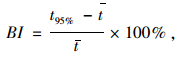
|
(9) |
式中,t95%为某时段内路段上所有行程时间的95%分位数。
根据式(2),采用基于风险型问题决策中的最大可能准则,定义行程时间阈值Ti, L为期望行程时间与可接受的延误时间之和。其中,期望行程时间为统计拟合分布的最大概率行程时间,则行程时间可靠度计算公式为:
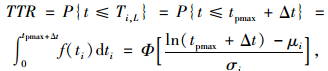
|
(10) |
式中,Φ(·)为标准正态分布函数;tpmax为某时段内统计拟合分布的最大概率行程时间;Δt为可接受的延误时间,即缓冲时间。可接受的延误时间为tpmax的5%,10%,15%或20%。由2.3节可知,采用最小二乘估计对阈值tpmax进行标定。
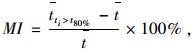
|
(11) |
式中tti>t80%为按由小到大排列的在后20%的行程时间均值,20%比例的选择是从经验得到的。
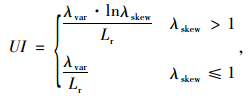
|
(12) |
式中,λvar为行程时间分布的宽度;λskew为行程时间分布的斜度;Lr为路段长度。
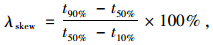
|
(13) |
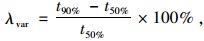
|
(14) |
式中,t10%,t50%,t90%分别为行程时间的10%,50%,90%分位数,t10%<t50%<t90%。
TTR属于正指标,值越大,可靠性水平越高;CV,BI,MI和UI属于负指标,值越小,可靠性水平越高。CV反映行程时间的离散程度;BI反映出行者为了以95%的概率准时到达目的地需要比平均行程时间多花费的时间;TTR为在可接受的时间内准时到达的概率;MI为不期望延误的严重程度;UI为遇到较差的可靠性状态的概率。这些指标接近出行者的实际感受,有助于在不确定性条件下做出合理的出行决策。
以10 km为间隔将样本数据分为15组,对样本进行随机抽样,每组样本容量为100 000个,分析0~150 km范围内客车和货车不同出行距离的可靠性,评价指标分析结果如表 3所示。
| 出行距离/km | 客车 | 货车 | ||||||||
| CV | BI/% | TTR/% | MI/% | UI | CV | BI/% | TTR/% | MI/% | UI | |
| 0~10 | 0.70 | 169.72 | 30.38 | 18.00 | 2.09 | 1.16 | 145.21 | 30.74 | 17.41 | 1.93 |
| 10~20 | 0.62 | 91.35 | 45.81 | 12.06 | 0.74 | 0.61 | 71.39 | 60.29 | 9.95 | 0.50 |
| 20~30 | 0.53 | 102.40 | 34.46 | 14.02 | 0.87 | 0.70 | 99.83 | 38.41 | 14.14 | 0.91 |
| 30~40 | 0.34 | 63.28 | 61.64 | 9.71 | 0.37 | 0.37 | 57.73 | 64.63 | 8.81 | 0.32 |
| 40~50 | 0.26 | 44.92 | 71.66 | 7.30 | 0.20 | 0.28 | 47.52 | 72.61 | 7.91 | 0.22 |
| 50~60 | 0.23 | 41.07 | 77.48 | 6.84 | 0.17 | 0.31 | 49.96 | 70.69 | 8.10 | 0.24 |
| 60~70 | 0.24 | 41.46 | 73.09 | 6.96 | 0.17 | 0.28 | 46.18 | 73.91 | 7.18 | 0.21 |
| 70~80 | 0.24 | 41.16 | 75.24 | 6.76 | 0.17 | 0.37 | 57.85 | 69.59 | 8.12 | 0.32 |
| 80~90 | 0.24 | 40.42 | 75.66 | 6.65 | 0.16 | 0.31 | 50.01 | 70.43 | 7.77 | 0.25 |
| 90~100 | 0.21 | 36.80 | 76.21 | 6.43 | 0.14 | 0.30 | 47.98 | 73.15 | 7.22 | 0.23 |
| 100~110 | 0.21 | 36.42 | 75.58 | 6.20 | 0.13 | 0.28 | 45.49 | 73.84 | 7.02 | 0.21 |
| 110~120 | 0.20 | 33.21 | 80.44 | 5.47 | 0.11 | 0.29 | 46.44 | 74.20 | 7.20 | 0.21 |
| 120~130 | 0.19 | 33.45 | 80.36 | 5.71 | 0.12 | 0.29 | 46.10 | 73.97 | 6.97 | 0.21 |
| 130~140 | 0.20 | 34.70 | 78.96 | 5.82 | 0.12 | 0.30 | 48.69 | 71.39 | 7.42 | 0.23 |
| 140~150 | 0.20 | 34.28 | 81.79 | 5.81 | 0.12 | 0.31 | 48.48 | 73.03 | 7.12 | 0.23 |
由表 3可知,客车和货车的CV,BI,MI和UI随出行距离的增加逐渐变小,TTR随出行距离的增加呈增长趋势,当出行距离大于60 km时,趋近于一个稳定状态。可见,客车和货车的行程延误受出行距离的影响显著。与长距离出行相比,客车和货车在短距离出行时TTR较低,而CV,BI,MI和UI较高。这说明路网在短距离出行时易遭遇不确定因素,行程时间波动性大,即可靠性水平较低。
以1 h为间隔,将样本数据分为24组,每组样本容量为100 000个,分析客车和货车不同出发时段的可靠性,评价指标分析结果如表 4所示。
| 出发时段 | 客车 | 货车 | ||||||||
| CV | BI/% | TTR/% | MI/% | UI | CV | BI/% | TTR/% | MI/% | UI | |
| 00:00—01:00 | 0.68 | 70.39 | 70.06 | 10.01 | 0.50 | 0.60 | 84.67 | 38.38 | 11.40 | 0.68 |
| 01:00—02:00 | 0.67 | 68.82 | 74.39 | 9.76 | 0.48 | 0.56 | 80.16 | 40.61 | 10.89 | 0.61 |
| 02:00—03:00 | 0.67 | 71.64 | 69.39 | 10.13 | 0.52 | 0.56 | 79.81 | 41.82 | 10.83 | 0.60 |
| 03:00—04:00 | 0.65 | 70.76 | 67.40 | 10.04 | 0.50 | 0.52 | 77.61 | 40.78 | 10.63 | 0.57 |
| 04:00—05:00 | 0.42 | 60.16 | 70.16 | 8.87 | 0.35 | 0.46 | 72.55 | 43.40 | 10.14 | 0.49 |
| 05:00—06:00 | 0.55 | 64.92 | 72.52 | 9.62 | 0.42 | 0.46 | 68.43 | 48.34 | 9.73 | 0.45 |
| 06:00—07:00 | 0.44 | 60.52 | 81.85 | 9.13 | 0.36 | 0.71 | 77.65 | 50.13 | 10.78 | 0.60 |
| 07:00—08:00 | 0.58 | 66.22 | 77.92 | 9.74 | 0.43 | 0.94 | 84.72 | 50.90 | 11.72 | 0.77 |
| 08:00—09:00 | 0.74 | 75.96 | 65.27 | 10.97 | 0.59 | 0.70 | 78.52 | 52.75 | 10.92 | 0.62 |
| 09:00—10:00 | 0.53 | 69.89 | 63.60 | 10.15 | 0.47 | 0.64 | 77.05 | 52.34 | 10.77 | 0.58 |
| 10:00—11:00 | 0.46 | 67.71 | 63.68 | 10.02 | 0.44 | 0.53 | 72.35 | 51.05 | 10.28 | 0.50 |
| 11:00—12:00 | 0.44 | 66.19 | 68.00 | 9.98 | 0.42 | 0.49 | 70.54 | 51.48 | 10.11 | 0.47 |
| 12:00—13:00 | 0.47 | 65.48 | 73.87 | 9.89 | 0.41 | 0.46 | 69.31 | 51.06 | 10.02 | 0.45 |
| 13:00—14:00 | 0.42 | 63.26 | 72.30 | 9.63 | 0.38 | 0.50 | 71.63 | 50.06 | 10.27 | 0.49 |
| 14:00—15:00 | 0.42 | 64.16 | 69.08 | 9.68 | 0.39 | 0.56 | 76.08 | 48.05 | 10.72 | 0.55 |
| 15:00—16:00 | 0.42 | 64.52 | 68.11 | 9.66 | 0.40 | 0.59 | 77.41 | 48.36 | 10.83 | 0.58 |
| 16:00—17:00 | 0.43 | 65.87 | 66.20 | 9.82 | 0.43 | 0.61 | 77.08 | 49.05 | 10.81 | 0.57 |
| 17:00—18:00 | 0.44 | 65.05 | 64.77 | 10.07 | 0.44 | 0.60 | 76.70 | 48.77 | 10.77 | 0.57 |
| 18:00—19:00 | 0.45 | 67.19 | 67.69 | 9.75 | 0.41 | 0.58 | 75.44 | 49.77 | 10.65 | 0.55 |
| 19:00—20:00 | 0.47 | 68.17 | 70.80 | 9.57 | 0.41 | 0.58 | 76.36 | 48.63 | 10.67 | 0.56 |
| 20:00—21:00 | 0.46 | 64.28 | 73.09 | 9.42 | 0.40 | 0.60 | 77.08 | 46.56 | 10.66 | 0.57 |
| 21:00—22:00 | 0.53 | 63.70 | 75.23 | 9.22 | 0.40 | 0.63 | 79.62 | 45.25 | 10.92 | 0.61 |
| 22:00—23:00 | 0.57 | 65.01 | 73.95 | 9.43 | 0.42 | 0.64 | 82.61 | 43.71 | 11.14 | 0.66 |
| 23:00—00:00 | 0.56 | 64.54 | 70.52 | 9.45 | 0.41 | 0.61 | 82.43 | 41.19 | 11.11 | 0.65 |
由表 4可知,路网中客车在时段08:00—11:00和16:00—18:00内TTR较其他时段低,且MI和UI较高,说明客车在高峰时段遭遇不可靠出行的机率较大,可靠性较非高峰时段低。对于货车而言,每天不同时段单位距离的CV,BI,TTR,MI和UI变化较客车小,说明货车的行程延误受出发时段的影响不显著。
4 结论为消除不同车型速度差对可靠性计算结果的影响,将货车和客车分别进行分布拟合,验证了高速公路网中单位距离的行程时间服从对数正态分布。
选取误差平方和(SSE)、累积分布函数的误差平方和(SSE of CDF)、确定系数(R2)、偏度系数的相对误差(RES)和峰度系数的相对误差(REK)5个指标来衡量,比较了不同参数估计的拟合效果,给出了不同参数估计方法的适用情况。结果表明,基于对数正态分布的路径行程时间可靠性模型能够准确估算路径的行程时间可靠度;最大似然估计在拟合单位距离行程时间累积概率分布时误差较小;最小二乘估计在拟合单位距离行程时间的偏态性和峰值时误差更小。
可接受行程时间阈值会影响可靠性评价结果。本研究提出了面向出行者的行程时间阈值选取方法,将模型应用于陕西省高速公路网,对行程时间可靠性进行了评价。评价结果表明,出行距离对货车和客车的行程时间可靠度均有影响,出发时段对客车的出行延误影响比货车大。如何运用CV,BI,TTR,MI和UI指标来综合评价该路段或该时段的服务水平和运行质量是需要进一步解决的问题。
| [1] | Federal Highway Administration. Traffic Congestion and Reliability:Trends and Advanced Strategies for Congestion Mitigation[R]. Washington, D.C.:Federal Highway Administration, 2005. http://www.worldcat.org/title/traffic-congestion-and-reliability-trends-and-advanced-strategies-for-congestion-mitigation/oclc/62324134 |
| [2] | 侯立文, 谭家美. 信息条件下路段出行时间可靠性的计算[J]. 上海交通大学学报 , 2006, 40 (6) : 968-972 HOU Li-wen, TAN Jia-mei. Computing the Link Travel Time Reliability with Information Provision[J]. Journal of Shanghai Jiaotong University , 2006, 40 (6) : 968-972 |
| [3] | 柏喜红, 陈旭梅, 王莹, 等. 高速公路行程时间可靠性研究综述[J]. 交通运输工程与信息学报 , 2014, 12 (2) : 70-76 BAI Xi-hong, CHEN Xu-mei, WANG Ying, et al. Review on Travel Time Reliability Research of Freeways[J]. Journal of Transportation Engineering and Information , 2014, 12 (2) : 70-76 |
| [4] | 王婧, 何杰, 吴炼. 雨天高速公路网行程时间可靠性评价方法[J]. 交通运输系统工程与信息 , 2011, 11 (6) : 117-123 WANG Jing, HE Jie, WU Lian. Evaluating Approach of Travel Time Reliability for Highway Network under Rain Environment[J]. Journal of Transportation Systems Engineering and Information Technology , 2011, 11 (6) : 117-123 |
| [5] | 叶佳缘, 杨赛霓, 刘浩. 降雨对高速公路小型车行程时间的影响[J]. 公路交通科技 , 2012, 29 (11) : 135-139 YE Jia-yuan, YANG Sai-ni, LIU Hao. Impact of Rainfall on Freeway Travel Time for Passenger Cars[J]. Journal of Highway and Transportation Research and Development , 2012, 29 (11) : 135-139 |
| [6] | 吴炼, 李旭宏, 王婧, 等. 雾天高速公路网行程时间可靠性评价方法[J]. 解放军理工大学学报:自然科学版 , 2010, 11 (2) : 233-238 WU Lian, LI Xu-hong, WANG Jing, et al. Reliability Evaluation on Travel Time in Freeway Network under Fog Environment Influence[J]. Journal of PLA University of Science and Technology:Natural Science Edition , 2010, 11 (2) : 233-238 |
| [7] | 冷军强.冰雪条件下城市路网行程时间可靠性研究[D].哈尔滨:哈尔滨工业大学, 2010. LENG Jun-qiang. Travel Time Reliability of Urban Road Network under Ice and Snowfall Conditions[D]. Harbin:Harbin Institute of Technology, 2010. http://www.cnki.com.cn/article/cjfdtotal-hebx201004021.htm |
| [8] | 陈玲娟, 刘海旭, 蒲云. 交通事故持续期内行程时间的可靠性研究[J]. 西南交通大学学报 , 2013, 48 (2) : 376-382 CHEN Ling-juan, LIU Hai-xu, PU Yun. Travel Time Reliability during Incident Duration Time[J]. Journal of Southwest Jiaotong University , 2013, 48 (2) : 376-382 |
| [9] | BELL M G H, LIDA Y. Transportation Network Analysis[M]. New York: John Wiley & Sons, 1997 . |
| [10] | AREZOUMANDI M. Estimation of Travel Time Reliability for Freeways Using Mean and Standard Deviation of Travel Time[J]. Journal of Transportation Systems Engineering and Information Technology , 2011, 11 (6) : 74-84 |
| [11] | 陈琨, 于雷. 基于对数正态和分布的路径行程时间可靠性模型[J]. 北京交通大学学报 , 2009, 33 (3) : 35-39 CHEN Kun, YU Lei. Route Travel Time Reliability Model Based on Lognormal Sum Distribution[J]. Journal of Beijing Jiaotong University , 2009, 33 (3) : 35-39 |
| [12] | 尹志鹏, 刘伟铭, 庄岩浩. 基于高速公路收费数据的旅行时间可靠性分析[J]. 公路与汽运 , 2014 (5) : 52-57 YIN Zhi-peng, LIU Wei-ming, ZHUANG Hao-yan. Analysis on Travel Time Reliability Based on Data of Expressway Toll[J]. Highways & Automotive Applications , 2014 (5) : 52-57 |
| [13] | 唐俊.基于浮动车数据的高速公路路段行程时间预测方法研究及系统实现[D].广州:中山大学, 2011. TANG Jun. Research on Freeway Link Travel Time Prediction Based on Float Car Data and System Implementation[D]. Guangzhou:Zhongshan University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10558-1012004553.htm |
| [14] | 刘克.高速公路的路段行程时间估计与预测方法研究[D].北京:北京交通大学, 2013. LIU Ke. Estimation and Prediction Method for Link Travel Time of Freeways[D]. Beijing:Beijing Jiaotong University, 2013. http://cdmd.cnki.com.cn/article/cdmd-10004-1013278482.htm |
| [15] | 王浩.基于收费数据的高速公路旅行时间自适应插值卡尔曼滤波预测研究[D].北京:北京交通大学, 2014. WANG Hao. Research on Expressway Travel Time Prediction Using Adaptive Interpolation Kalman Filter Based on Toll Collection Data[D]. Beijing:Beijing Jiaotong University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10004-1014177864.htm |
| [16] | ZHOU X H. Estimation of the Log-normal Mean[J]. Statistics in Medicine , 1998, 17 (19) : 2251-2264 |
| [17] | TARALDSEN G. A Precise Estimator for the Log-normal Mean[J]. Statistical Methodology , 2005, 2 (2) : 111-120 |
| [18] | 于洋. 对数正态分布的几个性质及其参数估计[J]. 廊坊师范学院学报:自然科学版 , 2011, 11 (5) : 8-11 YU Yang. Several Properties of the Lognormal Distribution and Estimation of Its Parameters[J]. Journal of Langfang Teachers University:Natural Science Edition , 2011, 11 (5) : 8-11 |
| [19] | 庄岩浩.基于收费数据的高速公路旅行时间可靠性分析与应用[D].广州:华南理工大学, 2014. ZHUANG Yan-hao. Analysis and Application of Expressway Travel Time Reliability Based on Toll Data[D]. Guangzhou:South China University of Technology.2014. http://cdmd.cnki.com.cn/article/cdmd-10561-1014063777.htm |
 2016, Vol. 33
2016, Vol. 33
