扩展功能
文章信息
- 丁宏飞, 刘硕智, 秦政
- DING Hong-fei, LIU Shuo-zhi, QIN Zheng
- 基于模型预测控制的城市快速路交通协同控制
- Coordinated Traffic Control for Urban Expressway Based on Model Predictive Control
- 公路交通科技, 2016, 33(10): 111-117
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 111-117
- 10.3969/j.issn.1002-0268.2016.10.017
-
文章历史
- 收稿日期: 2015-08-05
2. 西南交通大学 交通运输与物流学院, 四川 成都 610031
2. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu Sichuan 610031, China
城市快速路具有便捷、舒适、高通过能力等诸多优势。为提高快速路服务能力,避免拥堵、事故等交通事件发生,国内外学者进行了诸多理论研究和工程实践。从控制手段看,快速路控制可分为入口匝道控制、可变限速控制、路径诱导等类别[1];从控制策略看,快速路控制经历了定时控制、感应控制、最优控制、集成控制等阶段[2]。Papageorgiou在Payne基础上,提出了用于描绘连续交通流时空变化的二阶METANET模型,为交通流预测提供了有效工具[3];Kotsialos等人基于METANET模型提出了快速路的集成控制方法,并讨论了多匝道协同问题[4];不同于以往开环控制,Bellemans等人利用闭环的模型预测控制(Model Predictive Control,MPC)处理控制问题,增强了模型鲁棒性[5];此后,可变限速、主路控制等策略被引入到快速路最优控制问题中,增加了控制手段的多样性[1-6]。此外,国内的孙静怡、陆小芳等人也就限速控制、快速路匝道控制等问题进行了有益的探讨[7-8]。
MPC策略具有滚动优化、反馈校正等优点,目前此类问题研究多集中在鲁棒性、求解效率和精度等方面。且此类问题的研究几乎都以总时间花费(TTS)最小为优化目标,而少有文章探讨该目标适用性。Papageorgiou虽指出了以TTS最小为目标的函数等价于以总流出量的时间加权值最大为目标的函数[2],但并未进一步探讨该等价关系对于模型优化效果的影响。此外,考虑到基于MPC的快速路协同控制问题属于NP hard问题,则在实际应用时,需要将大的系统拆解为多个子区,并对子区进行协同控制,但目前仍少有此方面的研究。
本文改进了快速路控制优化问题的目标函数形式,以更好体现系统整体效益;此外提出了一种用于多个快速路子区协同控制的方法模型,以确保在不显著影响求解精度的前提下提高求解速度。算例表明,本文方法取得了优于现有方法的求解结果。
1 宏观交通流模型 1.1 METANET二阶模型本文采用METANET二阶模型描述交通流状态, 该模型具有形式简洁、解释力强、参数标定简便等优点。下面对其基本形式进行描述,更细致阐述可参见文献[3]。
将快速路网描述为有向网络,网络的每一条有向弧表示一段连续的、道路特征相似的且无道路分岔或汇聚的路段m;每一路段被分为等长的Nm个长度为Lm车道数为λm的子段i。每一子段由交通密度ρm, i(k)和平均速度vm, i(k)描述,其中k表示时段,t=kTs,Ts为预测步长。qm, i(k)表示m路段i子段的交通流量;qm, ir(k)表示进口匝道交通流量;sm, i(k)表示出口匝道交通流量;rm, i(k)表示匝道调解率; vf, m为自由流速度;ρcr, m为临界密度;τ, κ, ψ,v, αm是常数,需依据道路交通情况进行标定。可由式(1)计算每一步长交通量。

|
(1) |
交通密度ρm, i(k)和平均速度vm, i(k)的守恒方程可分别描述为:

|
(2) |

|
(3) |
式中V[ρm, i(k)]为稳态速度,它由密度ρm, i(k)决定。

|
(4) |
(1) 上匝道控制模型
上匝道控制是最常见快速路控制手段,该方法通过调节匝道绿信比来控制单位时间内进入快速路的车辆数。单位时间内流入快速路的车辆数可由式(5)计算。

|
(5) |
式中,dm, i(k)为上匝道交通需求;ωm, i(k)为上匝道排队; rm, i(k)为匝道控制率; C0为进口匝道的通行能力; ρmax为阻塞密度;ρcr为临界密度。排队可由式(6)计算。

|
(6) |
由式(5)可以发现,上匝道调解率rm, i(k)决定了k时段内进入快速路的车辆数qm, ir(k),而qm, ir(k)通过式(2)对交通流方程产生影响,因而式(5)建立了上匝道控制与宏观交通流的关系。
(2) 可变限速控制模型
在图 1中,实线为基本图,它描述了流量与密度的变化关系,即在点1前,车辆以自由流行驶,流量随密度增大而增大; 在点1之后,交通流变得拥挤,车辆速度下降,则流量随密度增加而下降。图中虚线则表示限速50 km/h时的基本图变化,即在此限速下,自由流速度被降低到50 km/h,则在低密度区其流量低于未限速情况;但若在点1附近时实时可变限速,则点1状态被转变为图中点2, 3间的某一状态,即通过可变限速,将一种不稳定的交通状态转变为一种稳定的交通状态。

|
| 图 1 可变限速控制机理 Fig. 1 Mechanism of variable speed limit control |
| |
从图 1看到,可变限速实际是决定了速度的上限,则若未实施可变限速时某密度下的稳态速度为V′[ρm, i(k)],可变限速值为Vctrl, m, i(k),那么可变限速下的稳态速度则为:

|
(7) |
式中α是考虑驾驶员遵守情况所做的修正。联立式(7)与式(4),则式(4)被修正为:

|
(8) |
至此,便建立了描述可变限速的数学模型。
(3) 交通诱导模型
图 2是包含快速路主路、辅路的一个测试路网。图中RAMP为上匝道控制器,VSL为可变限速控制器,VMS则为交通诱导屏。

|
| 图 2 测试路网 Fig. 2 Test road network |
| |
交通诱导模型可如下描述:设在k时段辅路路段4上交通流量为qm, if(k),并设流量在该段的分离率为β0m,
现引入交通诱导的可变情报板(variable message sign, VMS), um, if(k)表示VMS所处的状态。

|
(9) |
则有诱导下路段分离率为:

|
(10) |
式中,ζ为驾驶者对交通诱导的服从比率, 则式(10)对交通诱导的作用机理进行了模型化解释。
2 模型预测控制的基本原理首先区分预测步长Ts和控制步长Tc。Ts是预测模型仿真步长,本文取15 s,Tc为控制器的控制周期,一般为Ts的整数倍,即Tc=M·Ts,其中M为指定常数;第k个预测周期和第kc个控制周期则分别对应时段kTs和kcTc。由此可见,一个控制周期包括了多个预测周期,反映成函数形式则为:

|
(11) |
式中, x(k)为第k预测周期的状态向量; u(kc)为第kc控制周期的控制向量; d(k)为第k预测周期的扰动向量。
应用式(11)对仿真时段{k, …, k+MNP-1}循环迭代,则可得到该仿真时段内各预测周期的系统状态,其中NP为预测时间跨度(以控制步长为单位)。
第k期扰动矩阵和状态矩阵分别为:

|
(12) |

|
(13) |
第kc期控制矩阵为:

|
(14) |
对于MPC控制,由于其求解复杂,故为提高计算效率一般令控制时间跨度Nc≤Np,对于超出空置时间跨度的控制向量,则令其等于:

|
(15) |
上述式(11)~(15)表述了MPC控制中控制矩阵U(kc)、扰动矩阵D(k)及状态矩阵


目前关于快速路的最优控制及模型预测控制基本都以总时间花费(total time spend,TTS)最小为目标。其对应的MPC目标函数形式为:

|
(16) |
现令

|
(17) |
则式(16)转化为:

|
(18) |
式中,N(j)为第j仿真时段内快速路系统中的车辆数。假设Qr(j)为j仿真时段系统总的需求量,S(j)为系统总的车辆流出量,便有

|
(19) |
则代入式(18)可得:

|
(20) |
若假设各周期内交通需求固定且已知,则上式中前2项均为定值,因而式(20)的最小值问题转化为式(21)的最大化问题。

|
(21) |
从上式看到,以TTS最小值为目标的优化函数(16)可转化成为以流出量关于时间加权值最大为目标的优化函数(21)。下面采用图 2对式(21)含义进行解释,其中图 2的基本参数信息如表 1所示。
| 类别 | ZONE(区域) | 子段 | 长度/m | 车道数 | RAMP数量 | VSL数量 |
| 参数 | 3 | 18 | 500 | 2 | 3 | 6 |
根据分析,以TTS为目标函数会存在以下3方面弊端:
(1) 未能综合考虑系统整体效益
根据式(21)的含义,系统的运行水平优劣只与流出量有关,则子段18处的车辆流出决定了该系统的运行水平,换言之,该路网的运行水平将随子段18处车辆流出的时间加权值的增加而增大,而与剩余17个子段的运行状态的好坏无关,即只要在预测时域内子段18保持高流出量,剩余17个子段即便发生堵塞也不会对系统运行水平的评价造成影响。这无疑将对整个系统的评价仅仅集中在有限个系统出口处,而未能考虑系统各部分的综合效益。
(2) 易生成恶化系统状态的控制方案
由式(2)、(3)所示,上游路段的流量和速度值分别会对下游路段的密度和速度值产生影响,且该影响按照模型的预测步长进行预测。如对于控制器VSL 1,设其在k时段生成控制策略DVSL1(k),则在k+1时段,其控制结果开始影响子段4,k+2时段影响子段5,…,直至k+15时段,其控制影响才将波及子段18,即才开始对系统的评价指标产生影响。假设MPC采用20步的仿真时域(即仿真时段为{k,…,k+19}),则在此时段内,控制器VSL 1共生成20组控制方案,而其中有5组对子段18,即对系统状态评价产生影响,其对系统的影响程度为5/20=25%。由此可见,系统对控制的评价有延迟性,下面通过表 2做进一步阐述。
| 仿真时域 | 影响程度/% | ||||||||
| VSL 1 | VSL 2 | RAMP 1 | VSL 3 | VSL 4 | RAMP 2 | VSL 5 | VSL 6 | RAMP 3 | |
| 20 | 25 | 30 | 35 | 55 | 60 | 65 | 85 | 90 | 95 |
| 30 | 50 | 53 | 57 | 70 | 73 | 77 | 90 | 93 | 97 |
| 40 | 63 | 65 | 68 | 78 | 80 | 83 | 93 | 95 | 98 |
由表 2可见,对于控制器VSL 1,VSL 2和RAMP 1,它们对系统TTS的影响程度均不超过70%,这说明有超过30%的控制方案未能纳入系统的评价。这样造成的不利后果主要有两点:一是在系统评价时却未能充分利用求解的结果,造成计算资源的浪费;二是有超过30%的控制方案未被纳入指标评价,极易导致生成了可能恶化系统状态的不利方案。
此外控制器对系统TTS指标的影响,一方面随着仿真时域的增加而增大,另一方面也随距系统出口的距离减小而增大,即若要保证控制器的影响程度和控制效果,一方面尽量增大系统的仿真时域,另一方面要尽量减小系统的规模。下面分析增大系统仿真时域导致的问题,而关于第二点则在后面进行讨论。增大系统仿真时域会造成两点困难:
(1) 计算复杂度呈指数增长
设系统控制器数量为Oc,每个控制器的方案选择数为Om,若控制器的时间跨度为Nc,则计算复杂度为:

|
(22) |
为保证模型预测效果,Nc相较于预测时间跨度Np不能过小,即Nc∝Np。不妨令Nc=θ·Np(0 < θ < 1),则代入式(18)得:

|
(23) |
式(23)表明,复杂度C随预测时间跨度Np的增加而成指数增长。因此,单纯依靠增大系统仿真时域来提高控制器的控制效果是不可行的。
(2) 模型预测效果受限
本文利用了METANET二阶交通流模型作为预测模型。该模型属于宏观交通流模型,利用平均密度和平均速度表征道路状态和演变趋势。该预测模型的预测精度主要受到3点限制:一是模型本身属于宏观模型,并不能完全精确描述交通流变化;二是模型参数需要标定,其标定精度影响模型预测结果;三是实际路网会受到各种干扰,交通需求也是随机而未知的,因此模型的扰动变量难以估计。基于上述3点,模型每步均会产生预测误差,而该误差随预测时域的增大而发散。因此,过大仿真时域会降低预测精度。
(3) 不利于进行系统分区控制
除增大系统仿真时域外,还可通过减小控制规模来提高控制方案的适应性,如将图 1的路网拆解成ZONE 1,ZONE 2和ZONE 3这3个子区进行系统分区控制。但对于以TTS为目标的函数,这样的做法并不合适。如假设对图 1系统进行拆解,则用于评价ZONE 1的指标变为子段6的流出量,评价ZONE 2的指标为子段12的流出量,评价ZONE 3的指标为子段18的流出量。若提高ZONE 1的运行效果,则需尽量提高子段6的流出量,但应该看到,子段6的流出量增加势必会对ZONE 2造成影响,因此为保证ZONE 2的运行效果,则需对ZONE 1的流出量进行限制。可以看到,这在逻辑上是存在矛盾的。
3.1.2 基于路段速度、密度的目标函数改进对3.1.1节所述的TTS目标函数的3点不足归纳可见,其适应性差的主要原因是:对系统的评价归结为对有限几个系统出口处的评价,而忽略了对系统中各路段综合效益的考察。
为此,本文将路段平均速度和平均密度指标纳入系统的评价指标体系构建目标函数,以确保对系统总体运行状态的精确描述。该函数的形式为:

|
(24) |
下面针对TTS指标的3点不足,分别考察式(20)的效果。
(1) 对系统整体效益的反映
根据三相交通流理论[9],交通流共存在自由流、同步流和宽运动阻塞三相,三相间可发生一阶相变并引起capacity drop、回滞等现象。为避免相变的发生关键在于控制路网密度在临界密度之下。而根据速度与密度的基本图关系,速度随密度增加而下降。因此,将平均密度纳入评价函数以表征各路段状态,可防止交通流在临界密度附近出现的通行能力骤降。
为说明式(24)与TTS指标间的关系,向式(24)等式右侧乘以参数λm和Ts。由于该参数均为确定的定值,因此不会对式(20)的结果造成影响。其函数变形如式(25)所示。

|
(25) |
比较式(25)与式(21)可以发现,改进后的目标函数不同于TTS,它将系统中各子段的流出量均纳入到评价体系之中,而不是仅考虑有限个系统出口处的效益。
(2) 控制策略的延迟性
在TTS指标中,随着系统的增大以及预测时域的减小,控制策略的延迟性呈增大趋势。该延迟性主要由于系统将评价指标归结为几个系统出口的指标。而在改进模型中,系统各部分的运行效果均被纳入评价体系,因此理论上讲不存在控制策略延迟性的问题。
(3) 系统分区控制问题
对于TTS指标来讲,图 2中ZONE 1,ZONE 2仅为整个路网系统的两个子区域,它们的TTS指标只是系统运行的一个中间过程,用该指标对ZONE 1,ZONE 2进行评价缺乏解释力。而对于改进模型来讲,由于该模型是对各路段综合效益的评价,因此即便进行分区控制,对各子区的评价仍具有物理含义,即避免各子区出现同步流或宽运动阻塞的一阶相变。
3.2 分区协同控制问题首先说明分区控制的必要性。式(23)给出了MPC控制方法的算法复杂度计算方法。现考察对于图 2的路网,当分别采用一体化控制,以及对ZONE 1,ZONE 2,ZONE 3进行分区协同控制时,其算法复杂度的取值。对于一体化控制,其控制器数量Oc=9,则算法复杂度为C1=(Om)9·θ·Np。对于分区控制,其每子区控制器数量为Oc=9/3=3,则系统算法复杂度为C2=3·(Om)3·θ·Np,两种策略的复杂度比值为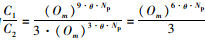

以图 2路网为例,对ZONE 1,ZONE 2和ZONE 3协同的关键在于协调3个子区域交通流出量的关系。一方面,各子段愈多的流出量有助于提高该子段的运行效果;但另一方面,上游子段过多的流出量会增大下游子段的负担。
本文的分区协同思路是,通过构造罚函数,利用闭环反馈的方法计算上游子区域的车辆流出量上限,以保证下游子区域的第一个路段的交通密度维持在临界密度之下,从而避免下游子区域一阶相变的出现。设子区域的流出量上限为Qmcr(k),则流出量上限值为:

|
(26) |
式中,ρmcr为下游子区域临界密度; kR为待定参数。利用式(26),则可构造罚函数为:

|
(27) |
由此,目标函数(24)被修正为:

|
(28) |
式(28)即为考虑分区协同控制的目标函数形式,该函数充分考虑了上游子区量可能对下游子区造成的影响,并利用罚函数Pm(k)对流出量加以限制,以保证系统的整体效益。
4 算例分析采用图 2路网进行案例分析,METANET模型的具体参数参见文献[10],模型求解算法参见文献[11],此处不再赘述。算例分别比较了:(1) 基于TTS目标以及基于改进目标函数的系统效益;(2) 集中控制与分区协同控制的控制效果和计算效率。
4.1 TTS目标及改进目标函数的系统效益分析设定可变限速控制方案的可选集合为{60, 70, 80, 90, 100},上匝道控制率方案的可选集合为{0.6, 0.7, 0.8, 0.9, 1.0}。基本参数取值为:Ts=15,M=8,Nc=「θ·Np,其中θ=0.5,仿真时间1 h。分别仿真:(1) 无交通控制; (2) 基于TTS目标的交通控制; (3) 基于改进目标的交通控制,并统一采用TTS作为3种方案的评价指标,通过对比相较于无交通控制的TTS减小量来评价两目标函数的效果和稳定性。如图 3所示,为不同Np取值下的评价结果。

|
| 图 3 两目标函数的TTS比较 Fig. 3 Comparison of TTS between 2 object functions |
| |
由图 3总结得到:
(1) 当Np较小时,改进模型的仿真结果明显优于TTS为目标函数的结果。且从图中看到,基于TTS的目标函数在Np较小时其纵坐标为负值,即不但未能减少总时间花费,反而比无控制情况耗费更多时间。这是由于当Np较小时,快速路控制器的影响范围在预测时间跨度内未能扩散至系统出口处,即存在一个或多个控制器的控制策略不会对评价函数造成影响。在此情况下,对于此类的控制器,则求解的控制策略将是随机的,并很可能求得会导致系统运行恶化的控制方案,进而造成快速路系统的服务水平恶化,TTS增加。
(2) 改进后的目标函数的运行稳定性明显优于基于TTS的目标函数的稳定性。由图 3看到,改进后模型实施效果的波动范围为0.19-0.03=0.16,且模型在Np=5时便趋于收敛;而原模型的波动范围则为0.21-(-0.12)=0.33,且模型在Np=7时仍未区域稳定。
(3) 当Np较大时,TTS目标函数的优化效果优于改进后模型的优化效果。这是由于原模型是以TTS最小为目标的评价函数,因此当预测时间跨度足够长时,其函数结果优于改进模型便不足为奇。但应当注意到,在实际应用中,过长的Np值将会导致计算复杂度的指数级增长,如在本算例中Np=7时程序运行时间在1 h 20 min左右;此外应注意到,在实际应用中,路网需求将是随机而未知的,那么随着Np值的增加,模型的预测精度将呈下降趋势。
4.2 集中控制与分区协同控制的比较保持仿真参数不变,对集中控制及分区协同控制的控制效果和计算效率进行比较。在进行集中控制时,应用式(24)作为目标函数进行计算;进行分区协同控制时,将图 2的快速路系统分为ZONE 1,ZONE 2和ZONE 3这3个子区,并利用式(24)作为目标函数进行控制。两种控制方式的运算结果如图 4所示。

|
| 图 4 集中控制与协同控制的实施效果 Fig. 4 Effects of centralized control and coordinated control |
| |
由图 4可以看到,集中控制的控制效果优于分区控制,但运算耗费时间显著高于分区控制。在实际应用中,由于在线控制对实时性的要求很高,因此分区控制可以取得更好的效益。
5 结论快速路最优控制与分区控制是提升快速路服务能力的重要途径。本文提出了改进MPC控制的目标函数形式,有效解决了原以TTS为目标函数的迟滞性等问题,经算例分析取得明显优于原函数的结果;同时本文提出了用于快速路子区系统控制的方法,经算例分析,该方法可在模型计算的精确性与效率间实现较好的平衡。
| [1] | HEGYI A. Model Predictive Control for Integrating Traffic Control Measures[D]. Delft:Netherlands TRAIL Research School, 2004. http://www.nexoncn.com/read/08d80db9314411a819ce058d.html |
| [2] | PAPAGEORGIOU M, KOTSIALOS A. Freeway Ramp Metering:An Overview[J]. IEEE Transactions on Intelligent Transportation Systems , 2003, 3 (4) : 271-281 |
| [3] | PAPAGEORGIOU M, BLOSSEVILLE J, HADJ-SALEM H. Modelling and Real-time Control of Traffic Flow on the Southern Part of Boulevard Peripherique in Paris:Part I:Modelling[J]. Transportation Research Part A:General , 1990, 24 (5) : 345-359 |
| [4] | KOTSIALOS A, PAPAGEORGIOU M, MESSNER A. Integrated Optimal Control of Motorway Traffic Networks[C]//Proceedings of the American Control Conference. San Diego, California:IEEE, 1999:2183-2187. |
| [5] | BELLEMANS T, DE SCHUTTER B, DE MOOR B. Model Predictive Control with Repeated Model Fitting for Ramp Metering[C]//Proceedings of 5th IEEE International Conference on Intelligent Transportation Systems. Singapore:IEEE, 2002:236-241. http://cn.bing.com/academic/profile?id=2144228342&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | HEGYI A, DE SCHUTTER B, HELLENDOORN H. Model Predictive Control for Optimal Coordination of Ramp Metering and Variable Speed Limits[J]. Transportation Research Part C:Emerging Technologies , 2005, 13 (3) : 185-209 |
| [7] | 孙静怡, 沈俊江, 刘拥华, 等. 城市快速路可变限速策略[J]. 公路交通科技 , 2012, 29 (11) : 98-103 SUN Jing-yi, SHEN Jun-jiang, LIU Yong-hua, et al. Variable Speed Limits Strategy of Urban Expressway[J]. Journal of Highway and Transportation Research and Development , 2012, 29 (11) : 98-103 |
| [8] | 陆小芳, 陈华, 虞鸿, 等. 城市快速道路入口匝道汇入控制应用-控制算法EXPAlinea[J]. 公路交通科技 , 2009, 26 (S1) : 132-136 LU Xiao-fang, CHEN Hua, YU Hong, et al. Field Application of On-ramp Merging Control of Urban Freeway:Control Algorithm EXPAlinea[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (S1) : 132-136 |
| [9] | KERNER B S. Three-phase Traffic Theory and Highway Capacity[J]. Physica A:Statistical Mechanics and Its Applications , 2004, 333 (1) : 379-440 |
| [10] | FREJO J R D, CAMACHO E F. Global Versus Local MPC Algorithms in Freeway Traffic Control With Ramp Metering and Variable Speed Limits[J]. IEEE Transactions on Intelligent Transportation Systems , 2012, 13 (4) : 1556-1565 |
| [11] | 孙立伟.基于VMS发布诱导信息的快速路网动态最优控制[D].杭州:浙江大学, 2013. SUN Li-wei. Dynamic Optimal Control of Urban Expressway via Variable Message Signs[D]. Hangzhou:Zhejiang University, 2013. |
 2016, Vol. 33
2016, Vol. 33
