扩展功能
文章信息
- 刘金升, 钱永久
- LIU Jin-sheng, QIAN Yong-jiu
- 外套钢管加固有初始力钢筋混凝土短柱结构承载力计算方法研究
- Study on Computational Method of Bearing Capacity of RC Short Columns with Initial Stress Strengthened by External Steel Tube
- 公路交通科技, 2016, 33(10): 96-103
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 96-103
- 10.3969/j.issn.1002-0268.2016.10.015
-
文章历史
- 收稿日期: 2016-03-04
目前对钢管混凝土短柱极限承载力及基本力学性能研究是较完善的。翰林海[1]根据大量的钢管混凝土承载力试验数据提出了钢管混凝土本构关系曲线、钟善桐[2]提出的钢管混凝土统一理论、蔡绍怀[3-4]教授应用极限平衡法对钢管混凝土极限承载力的研究以及陈宝春[5]对钢管混凝土桥梁的受力研究,都为钢管混凝土的承载力分析研究提供了很好的理论基础。NE Shanmugam和B Lakshmi[6]对钢-混凝土组合柱进行了试验研究,同时考虑了二次受力对组合构件承载力的影响。东南大学徐进和蔡健[7]对圆钢套管套箍方形混凝土柱轴心受压性能进行研究,得出初始应力对加固柱承载力的影响不显著。Kato[8]根据100多个圆形和方形钢管混凝土轴心受压柱的试验数据分析研究,提出了其承载力简化计算方法。周绪红、张素梅、刘界鹏[9]对圆钢管约束钢筋混凝土短柱的轴压力学性能试验研究,并根据试验结果和应力分析结果建立了圆钢管约束钢筋混凝土短柱的轴压承载力公式。程昌绪[10]对二次受力外包矩形钢筋混凝土加固柱进行了全过程非线性模拟分析研究,并提出了轴心受压正截面承载力的简化计算公式。王元丰、朱海斌、韩冰[11]对影响钢管混凝土受弯构件徐变的各种因素研究,采用回归分析的方法,得出了钢管混凝土受弯构件徐变计算公式。由于加固结构中核心混凝土的应力应变相对填充混凝土和套管有滞后现象,不能直接地把外套钢管加固钢筋混凝土柱作为钢管混凝土结构计算分析。虽然外套钢管加固钢筋混凝土柱做为桥梁维修加固中常用加固方式,但其承载力分析研究国内处于探索状态,本文借鉴于上述学者对钢管混凝土和围套加固混凝土结构的承载力研究,在总结钢管混凝土承载力计算及二次受力结构的承载力计算相关研究的成果上,改进了韩林海钢管混凝土本构模型使之适合二次受力结构的承载力计算研究,运用静力学推导有初始力轴压加固结构的承载力计算公式,为工程实际结构承载力计算提供支持。
1 加固结构承载力计算及改进混凝土应力-应变曲线 1.1 情况1加固结构基本假定(1)加固结构应变场为轴对称,填充混凝土与核心混凝土间完全黏结无滑移,加固后截面为平截面。不考虑混凝土收缩和温度的影响。钢管采用Von Mises屈服准则,三向受压混凝土屈服条件采用Сonsidere和Richartd试验线性式(1)和根据试验资料蔡绍怀建议非线性式(2),如下所示。
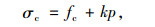
|
(1) |
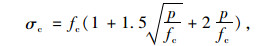
|
(2) |
式中,σc为三向受压混凝土抗压强度;fc为混凝土无侧压强度;p为侧压力;k为侧压系数。
(2)加固结构在原柱上施载,经原柱混凝土压力扩散后结构受力与局压钢管混凝土相似,加固后结构采用KLCO[12]局压承载力折减系数: KLCO=A·β+B·β0.5+C(参数含义见文献[12])。
(3)核心柱加固前为钢筋混凝土柱,其本构关系为Hognestad模型,参见文献[13],如式(3)所示。
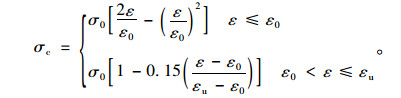
|
(3) |
本文要改进的韩林海模型,参见文献[14],如式(4)所示。
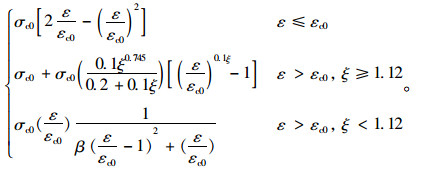
|
(4) |
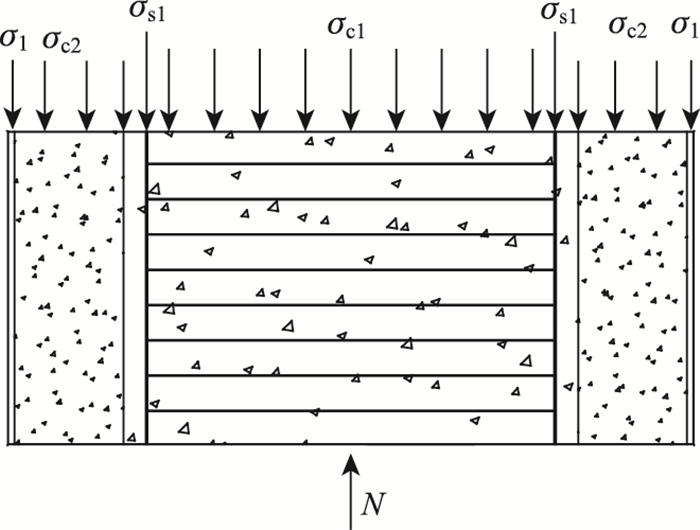
首先求加固后混凝土应力-应变曲线的拐点值,也就是套箍指标的临界分界值,其值决定了加固后混凝土在峰值点后的走向。加固后钢管、填充混凝土、核心混凝土的受力如图 1~图 4所示。
|
| 图 1 加固柱纵向承载受力简图 Fig. 1 Schematic diagram of longitudinal bearing capacity of reinforced column |
| |
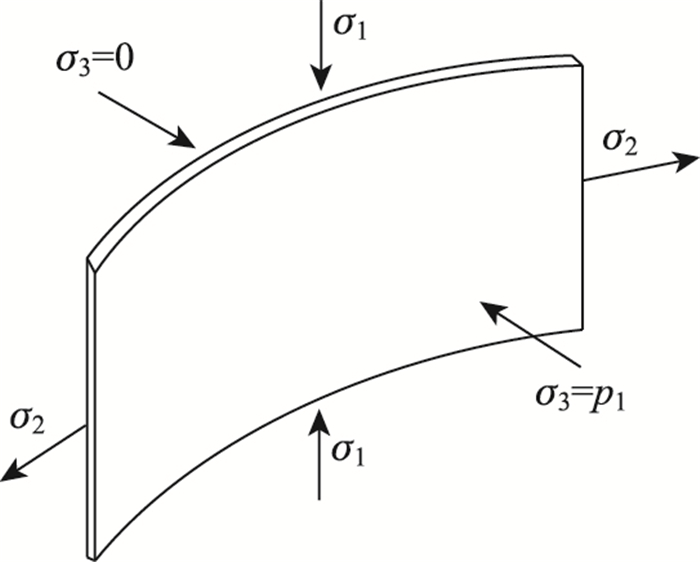
|
| 图 2 钢管微元受力图 Fig. 2 Force diagram of steel tube infinitesimal body |
| |
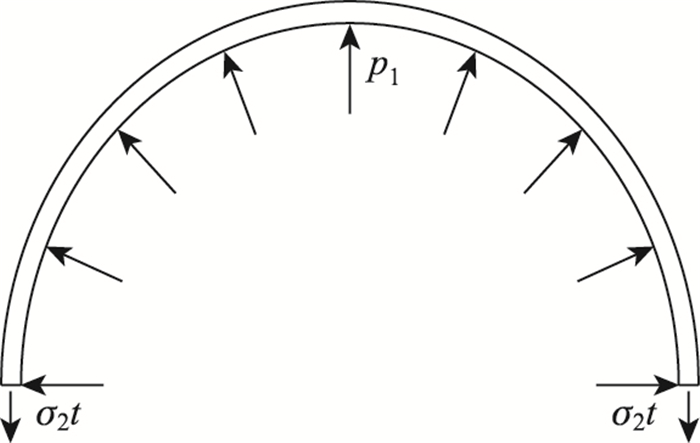
|
| 图 3 钢管径向受力简图 Fig. 3 Schematic diagram of radial force of steel tube |
| |
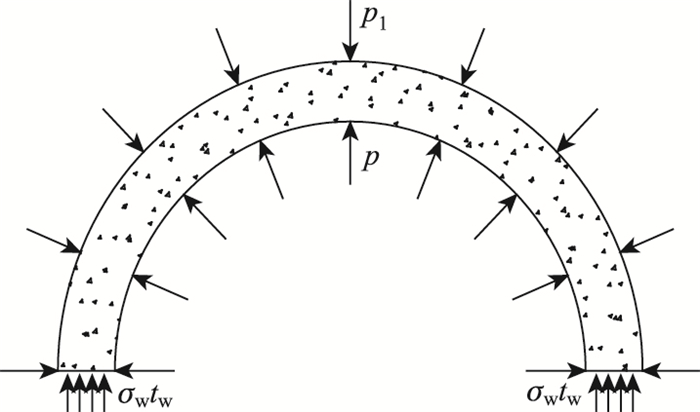
|
| 图 4 填充混凝土受力简图 Fig. 4 Schematic diagram of forces on filled concrete |
| |
由图 1建立静力平衡条件建立方程:
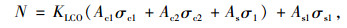
|
(5) |
式中,Ac1,Ac2,As,As1分别为核心混凝土、填充混凝土、钢管、纵筋横截面积;σc1,σc2,σs1分别为核心混凝土、填充混凝土、纵筋纵向应力;σ1和σ3分别为钢管的纵向、径向应力。
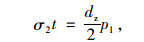
|
(6) |
式中,σ2为钢管环向应力; t为钢管的厚度; dz为加固后混凝土直径。
由图 4静力平衡方程可得:
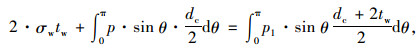
|
(7) |
式中,σw为填充混凝土环向应力;tw为填充混凝土;p1为填充混凝土对钢管内侧压应力;p为原柱混凝土对填充混凝土的径向压应力。
加固结构中,填充混凝土强度一般较原柱混凝土的强度等级高一两个等级,填充混凝土因受施加在核心柱上混凝土的轴向力的压力扩散,同时受钢管的约束而处于三向受压状态。由图 4对式(7)取σw=p1,则得:
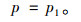
|
(8) |
由于加固结构套管内的混凝土由核心混凝土和填充混凝土构成,定义θ1=Asfs/(Ac1fc1),式中,θ1为加固钢管对原柱核心混凝土的套箍指标,fc1为核心混凝土的抗压设计强度,fs为钢管屈服极限强度。
对薄壁钢管有As/Ac1=4dz·t/dc2,则θ1=4dztfs/(dc2fc1),式中,dc为核心混凝土柱直径。
结构极限状态时,对核心柱混凝土有:p/fc1=dc2θ1/(2dz2)。
当核心混凝土的屈服条件线性为式(1)时单独原核心柱承载力为:
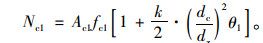
|
(9) |
核心混凝土的屈服条件线性为式(2)时单独原核心柱承载力为:
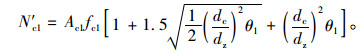
|
(10) |
令式(9)和式(10)相等,可求得θ1临界分界值[θ1]=1.125dz2/dc2。同理可求得填充混凝土套箍指标θ2的临界分界值[θ2]=1.125dz2fc1/(fc2dc2), 式中,fc2为填充混凝土的抗压设计强度。
加固后核心混凝土由单向轴压状态变为受钢管及填充混凝土约束的三向受压状态,故此采用三向等侧受压下混凝土强度提高的理论,加固后核心混凝土柱的抗压强度为σc=σ0(1+1.5 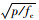
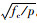
核心柱混凝土在加固前的应力-应变曲线为Hognestad公式,核心柱混凝土在二次受力时应力-应变曲线,可以认为原曲线起点应变应力(ε11, σ11)和曲线应变应力的峰值点(εc01, σ0+kp), 式中,ε11和σ11为核心柱初始应变和应力,εc01为加固后核心混凝土峰值应变。p值在核心混凝土加固时填充混凝土及钢管还无约束行为时p=0。当核心混凝土柱峰值应变εc01时,pmax=2fst/dz,kp应变区间为[ηεcr, ε01+ηεcr-ε11],其中:η=1+φc,φc为徐变系数,εcr为核心柱在恒载下的瞬时应变。
综合核心柱对填充混凝土径向压应力p的最小和最大值变化及其应变区间,采用线性插值的方式得p值在其应变区间值为[0,kpmax[2(ε-ηεcr)/(εc01-ε11)-(ε-ηεcr)2/(εc01-ε11)2], 式中,η=1+φc。二次受力时由于所考虑核心混凝土初始应力水平较低,加固后根据填充混凝土和原柱混凝土各自套箍系数代入韩林海钢管混凝土应变峰值公式,可求得填充混凝土和原柱混凝土各自的峰值应变。
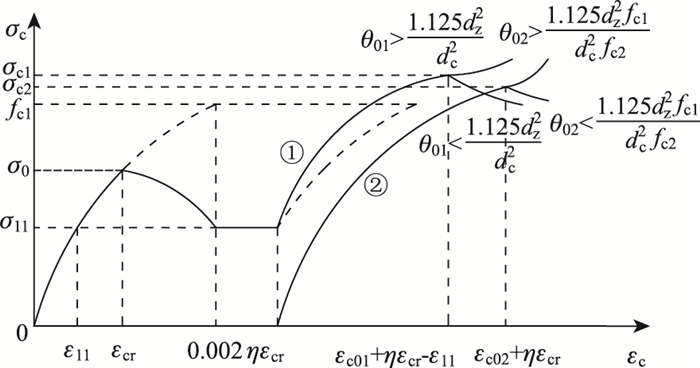
本文考虑的受徐变影响核心和填充混凝土本构关系如图 5所示。
|
| 图 5 受徐变影响核心和填充混凝土本构关系 Fig. 5 Constitutive relation of filling concrete and creep affected core |
| |
图 5中①线和②线分别为受徐变影响的核心和填充混凝土应力-应变曲线。其中:θ01和θ02为原柱和填充混凝土改进混凝土模型后的套箍系数,εc02为加固后填充混凝土峰值应变。
根据核心混凝土在加固前后的应力和应变连续性,以及二次受力时填充混凝土的应力应变滞后于核心混凝土,综合Hognestad模型和钢管混凝土本构模型及核心混凝土三向受压的屈服条件,可取加固后核心柱的混凝土应力-应变曲线Ⅰ和填充混凝土的应力-应变曲线如式(11)~(14)所示。
加固后核心混凝土应力-应变曲线Ⅰ为:
当ηεcr≤ε≤εc01+ηεcr-ε11时
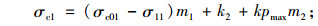
|
(11) |
当ε≥εc01+ηεcr-ε11时
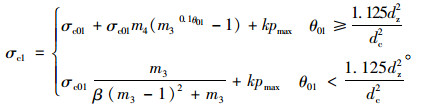
|
(12) |
上述式中,η=1+φc;
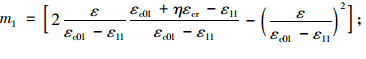
|
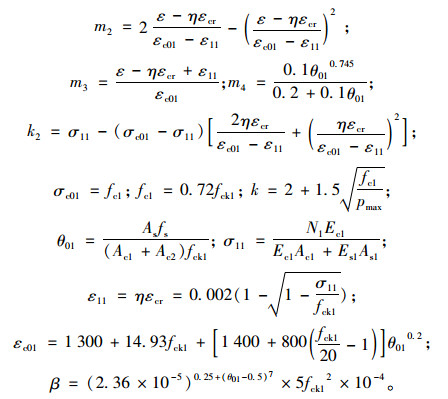
|
fck1为核心混凝土标准抗压强度; Ec1, Es1分别为核心混凝土、纵筋的弹性模量。
填充混凝土应力-应变曲线Ⅰ:
当ηεcr≤ε≤εc02+ηεcr时
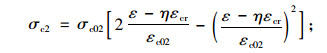
|
(13) |
当ε≥
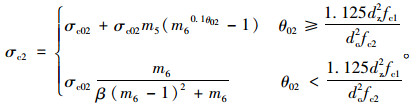
|
(14) |
上两式中:η=1+φc;m5=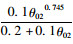
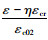
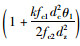
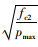
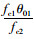
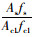
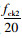
同理根据推导Ⅰ曲线的方法,考虑加固核心混凝土变形连续条件及加固后混凝土应变应力峰值点(εc01, σc01)可推出第2种加固后核心柱的混凝土应力-应变曲线Ⅱ为:
当ηεcr≤ε≤εc01+ηεcr-ε11时
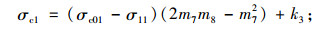
|
(15) |
当ε>εc01+ηεcr-ε11时
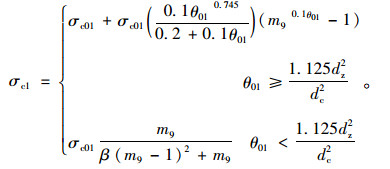
|
(16) |
上两式中:η=1+φc
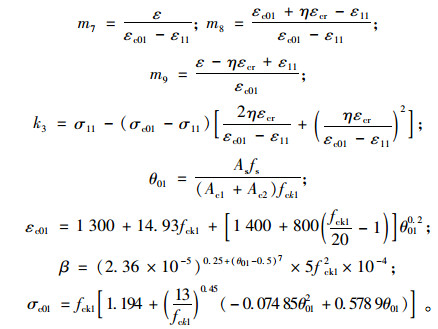
|
填充混凝土应力-应变曲线Ⅱ:
当ηεcr≤ε≤εc02+ηεcr时
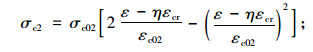
|
(17) |
当ε≥εc02+ηεcr时
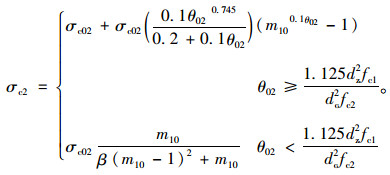
|
(18) |
式中:m10=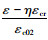
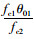
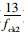
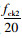
对核心柱混凝土应力-应变曲线为Ⅰ时。当θ01>1.125dz2/dc2时,由式(5)得:
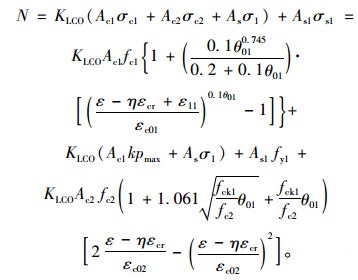
|
(19) |
式(19)中钢管的纵向压应力σ1由于本文中考虑的是核心混凝土初始力较低,因此认为在加固结构极限状态时采用文献[3]第3章式(3-19)的表达形式,取极限状态时σ1=0,fy1为钢筋屈服极限强度。为求式(19)的最大值,由dN/dε=0可求得对应于最大值时ε′的值,把ε′代入静力平衡方程(19)可求得加固结构极限承载力Nmax值。
同理可求得核心柱混凝土应力-应变曲线为Ⅰ时,当θ01 < 1.125dz2/dc2时Nmax的值。
对核心柱混凝土应力-应变曲线为Ⅱ时, 当θ01>1.125dz2/dc2时,由式(5)得:
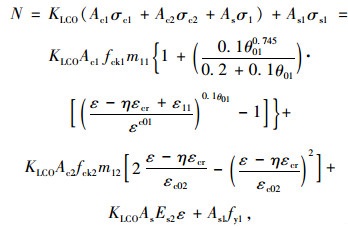
|
(20) |
式中,m11=1.194+(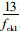
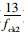
为求式(20)的最大值,由dN/dε=0可求得对应于最大值时ε′的值,把ε′代入静力平衡方程(20)可求得Nmax,此时Nmax为加固结构的极限承载力值。(使用核心柱混凝土曲线Ⅱ时,由于改进的核心混凝土模型是从韩林海混凝土的模型出发,此时外套钢管的本构模型取用弹塑性折线模型,这与核心柱混凝土曲线Ⅰ时钢管的本构关系不同)。
同理可求得核心柱混凝土应力-应变曲线为Ⅱ时,当θ01 < 1.125dz2/dc2时加固结构极限承载力Nmax的值。
2 试验算例 2.1 试件的制作及材料性能为取得加固结构混凝土试件极限承载力,在西南交通大学的长柱试验机进行了试验研究。由于同期有其他试验及试验经费的原因,本次试验共制作了两根钢筋混凝土短柱,其中一根为外套钢管加固混凝土柱J-1,其制作过程首先浇注原柱混凝土墩柱,待墩柱混凝土养护硬化后,在原墩柱表面凿毛后,使用钢套管加固,在钢套管和原柱混凝土间浇注填充细石混凝土。另一根为相同条件下但有初始应力的加固试件J-2。J-1和J-2加固试件的尺寸如表 1所示。
| 试件编号 | dc | h | t | tw | dj |
| J-1 | 250 | 1 000 | 4 | 25 | 6ϕ12 |
| J-2 | 250 | 1 000 | 4 | 25 | 6ϕ12 |
| 注: h为原墩柱高度,dj为纵筋直径。 | |||||
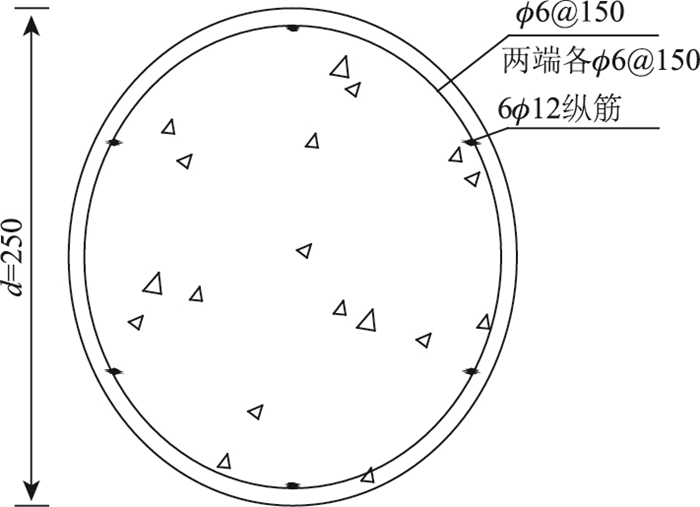
试件J-1和J-2截面尺寸及配筋分别如图 6和图 8及图 7和图 9所示。
|
| 图 6 原墩柱的截面示意图(单位:cm) Fig. 6 Schematic diagram of section of original pier column(unit:cm) |
| |
|
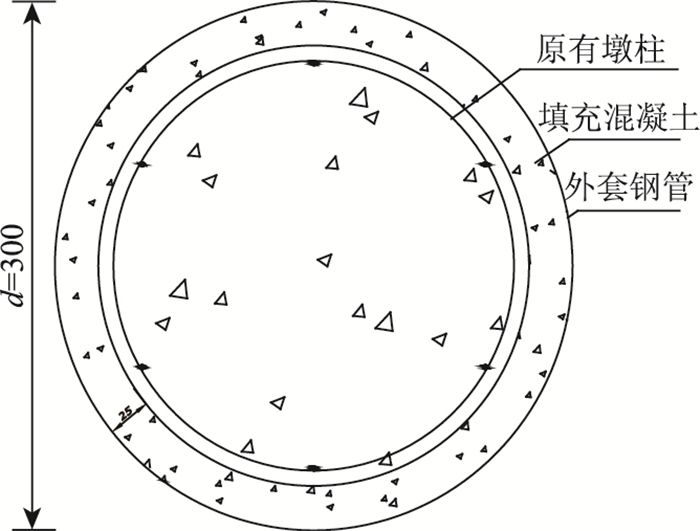
| 图 7 加固后结构截面示意图(单位:mm) Fig. 7 Schematic diagram of structure section after strengthening(unit:mm) |
| |
|
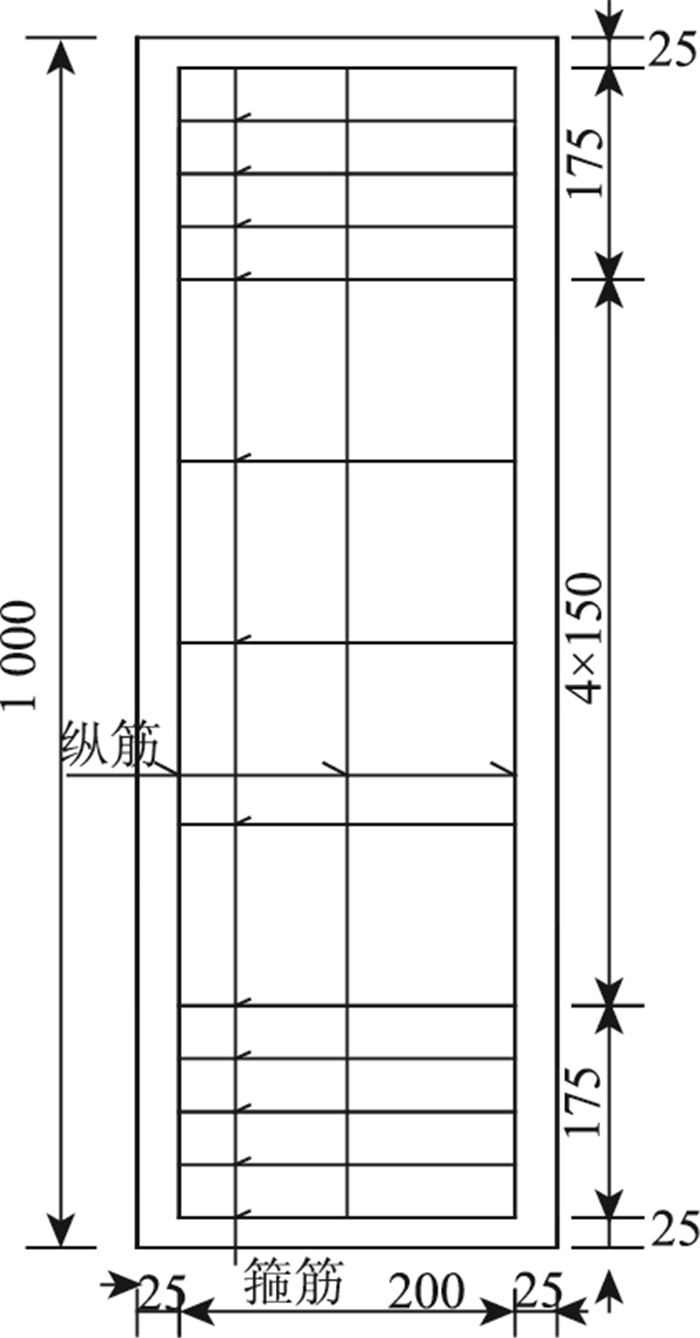
| 图 8 原墩柱的配筋图(单位:mm) Fig. 8 Reinforcement arrangement of original pier column(unit:mm) |
| |
|
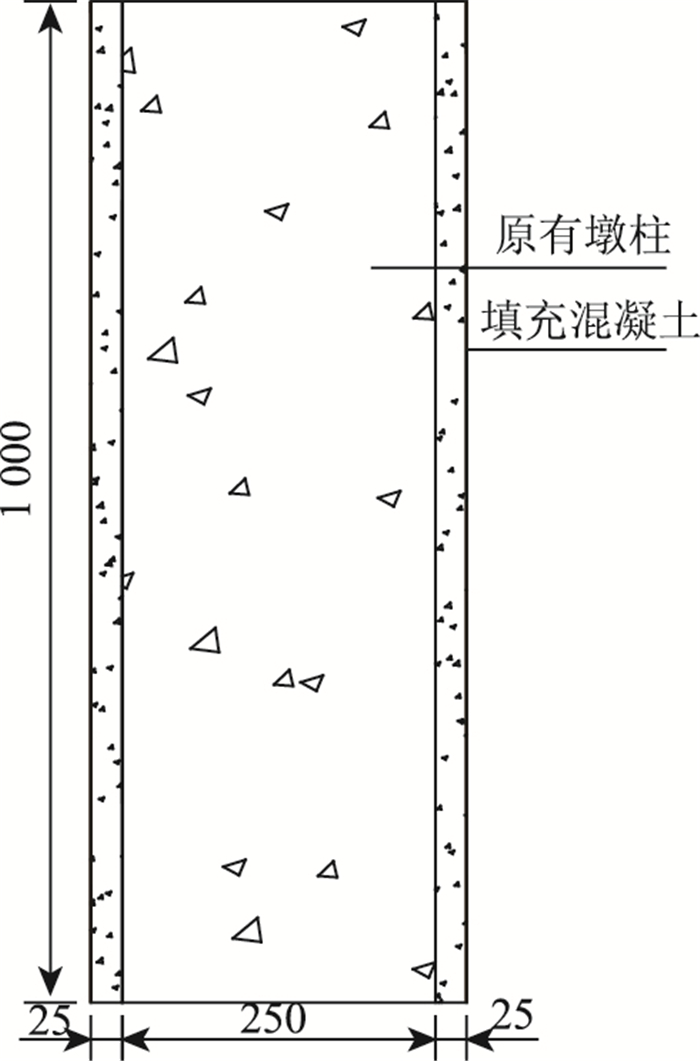
| 图 9 加固后结构钢管布置图(单位:mm) Fig. 9 Steel tube arrangement after strengthening(unit:mm) |
| |
原柱混凝土和填充混凝土强度均是由在实验室中相同条件下150 mm的立方体试块测得。填充混凝土和原柱混凝土的强度分别为38.1 MPa和36.3 MPa。
试验加固试件外套钢管为Q235钢板经卷板机卷曲后焊接而成,外套钢管的材料性能是根据外套钢管的厚度不同截取原材料做拉伸试验和焊接板拉伸试验。原柱纵筋与箍筋同样由预留的试件截取得到,按《金属拉伸试验方法》进行材性测试,外套钢管和钢筋力学性能如表 2所示。
| 材料 | 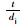 /mm
/mm | fuk/MPa | fyk/MPa | ftk/MPa |
| 钢管 | 4 | 336 | 279 | 302 |
| 钢筋 | 6.0 | 436 | 261 | — |
| 12.0 | 476 | 265 | — | |
| 注:表 2中t为钢管厚度; dj为钢筋直径; fuk为极限强度; fyk为屈服强度; ftk为焊缝抗拉强度。 | ||||
对有初始应力的原柱制作是在试件的中心预埋管子,当原柱试件浇注完自然养护后,在预留管孔内安放一根高强钢绞线,采用后张法对钢绞线进行张拉,预拉力为0.11倍的原柱极限承载力,即预先对试件施加轴向压力,然后两边进行锚固,并朝孔道中压入水泥浆。由于锚具在试件端头部,无法直接在试件端头施载,试验中在试件两端加厚垫层,将锚具藏在加厚垫层内,如图 10所示。

|
| 图 10 J-2试件 Fig. 10 Specimen J-2 |
| |
2.2 试验加载装置及加载程序和测量方法
J-1和J-2试件为静力加载,其试验为在西南交通大学最大加载为10 000 kN的长柱试验机上进行。加载程序参考文献[15]中第二章第二节1.2.1节中的加载方式,具体的试验加载程序为:
(1)在试验前准备放置好试件,把试件的两端找平,准备初始数据的记录。
(2)开动试验机,当压头与试件将要接触时,再次对试件调整找平。
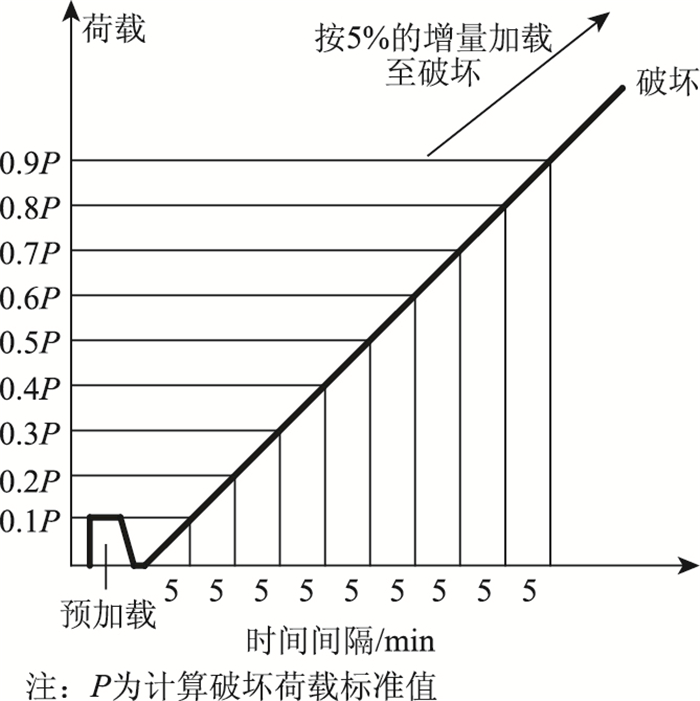
(3)在试验正式开始前,对试件进行预加载,同时查看试验机的运行情况。加载程序如图 11所示。
|
| 图 11 加载程序 Fig. 11 Loading program |
| |
正式加载时采用逐步分级加载,每级所加的荷载基本为破坏荷载的10%,每级加载完成以后,稳定停留5 min后进行下一级的加载,当荷载加载到90%的破坏荷载以后,按每级荷载的5%增量加载,逐步加载到试件破坏为止。
文中主要研究的是加固结构的极限承载力,因此试验的目的测量试件的极限承载力。对于试件J-1,试验中试验机得到的试验荷载即为试件J-1的极限荷载。而对于两阶段加载的二次受力J-2试件,试验机的荷载与预应力钢绞线施加的荷载之和为二阶段受力J-2试件上的承载力荷载,参照《混凝土结构试验方法标准》(GBJ50152—92),以整个试验阶段的最大荷载值作为极限荷载实测值。
2.3 试件极限承载力实测值和计算结果对比采用2.1节、2.2节的试验方法、加载程序及测量方法,通过试验得到的有初始力的外套钢管加固结构极限承载力如表 3所示。
| 试件 | Ng/kN | Ng1/kN | Ng2/kN | Ng1/Ng | Ng2/Ng |
| J-1 | 4 401 | 4 156 | 4 333 | 0.94 | 0.99 |
| J-2 | 4 396 | 4 145 | 4 325 | 0.94 | 0.98 |
| 注:Ng为试验承载力实测值; Ng1与Ng2为加固混凝土按应力-应变曲线Ⅰ和Ⅱ时计算的加固后结构的极限轴压承载力。 | |||||
表 3表明:本文所推导的两种有初始力加固结构承载力公式计算结果与试验实测值符合较好,是良好的计算有初始应力的二次受力结构的计算方法。
由于同期试验的关系,本文二次受力的试件较少,而文献[7]的试验条件、加载程序、测试方法与本文相似,为了进一步验证本文的计算方法,将本文的计算结果与文献[7]中5个试件的极限承载力实测值进行对比,如表 4所示。
| 试件 | Nt/kN | Ng1/kN | Ng2/kN | Ng1/Nt | Ng2/Nt |
| CZ1 | 2 780 | 2 356 | 2 777 | 0.85 | 0.99 |
| CZ2 | 3 678 | 3 435 | 3 548 | 0.93 | 0.96 |
| CZ3 | 3 030 | 2 355 | 2 776 | 0.78 | 0.92 |
| DZ1 | 4 290 | 3 580 | 3 646 | 0.83 | 0.85 |
| DZ2 | 4 230 | 3 578 | 3 641 | 0.83 | 0.86 |
| 注:Nt为试验承载力实测值。本文计算加固结构的承载力时,原方形柱横截面积等效成圆形柱进行计算。同时因文献[7]中是全截面加载,故此取KLCO=1,Ng1与Ng2为加固混凝土按应力-应变曲线Ⅰ和Ⅱ时计算的加固后结构的极限轴压承载力。 | |||||
表 4表明:通过对比,本文所推导的两种有初始力加固结构承载力公式计算结果与文献[7]试验实测值符合相对较好,进一步验证了本文计算公式的实用性。
3 结论本文通过改进韩林海本构模型及对有初始力的外套钢管加固钢筋混凝土短柱承载力的计算公式推导及试验研究,得出如下结论:
(1)对有初始应力的混凝土加固结构的承载力进行分析和计算,在混凝土Hognestad模型和韩林海本构模型的基础上,根据加固前核心柱的混凝土峰值应力、峰值应变与加固后加固核心柱混凝土有明显增加的应力应变的特点,按三向受压混凝土提高强度理论叠加对核心混凝土分别拟合了混凝土应力应变曲线Ⅰ和修正改进韩林海本构模型的核心混凝土应力应变曲线Ⅱ。使用加固后核心混凝土本构模型为应力-应变曲线Ⅰ和Ⅱ计算加固结构的承载力与试验的实测值进行对比,其计算结果与相关试验实测值符合较好,表明本文所推导的计算方法计算有初始应力的二次受力加固结构的良好可行性。
(2)通过本文推导的两种有初始力加固结构承载力公式计算结果与文献[7]试验实测值比较,二者符合较好,表明本文计算公式的外推实用性良好,可为同类加固结构承载力计算提供支持。
| [1] | 韩林海. 钢管混凝土结构[M]. 北京: 中国建筑工业出版社, 1999 : 101 -131. HAN Lin-hai. Steel Tube-confined Concrete Structure[M]. Beijing: China Architecture & Building Press, 1999 : 101 -131. |
| [2] | 钟善桐. 钢管混凝土结构[M]. 北京: 清华大学出版社, 2003 : 231 -268. ZHONG Shan-tong. Concrete-filled Steel Tubular Structure[M]. Beijing: Tsinghua University Press, 2003 : 231 -268. |
| [3] | 蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2003 : 35 -52. CAI Shao-huai. Modern Steel Tube Confined Concrete Structure[M]. Beijing: China Communications Press, 2003 : 35 -52. |
| [4] | 蔡绍怀, 焦占拴. 钢管混凝土短柱的基本性能和强度计算[J]. 建筑结构学报 , 1984, 5 (6) : 13-29 CAI Shao-huai, JIAO Zhan-shuan. Behavior and Ultimate Strength of Short Concrete-filled Steel Tubular Columns[J]. Journal of Building Structures , 1984, 5 (6) : 13-29 |
| [5] | 陈宝春. 钢管混凝土拱桥[M]. 北京: 人民交通出版社, 2007 : 555 -806. CHEN Bao-chun. Concrete Filled Steel Tubulur Arch Bridges[M]. Beijing: China Communications Press, 2007 : 555 -806. |
| [6] | SHANMUGAM N E, LAKSHMI B. State of the Art Report on Steel-Concrete Composite Columns[J]. Journal of Constructional Steel Research , 2001, 57 (10) : 1041-1080 |
| [7] | 徐进, 蔡健. 圆形钢套管加固方形混凝土柱轴心受压性能[J]. 东南大学学报 , 2006, 36 (4) : 580-584 XU Jin, CAI Jian. Behaviour of Square Reinforced Concrete Column Strengthened by Circular Steel Jacket under Axial Loading[J]. Journal of Southeast University , 2006, 36 (4) : 580-584 |
| [8] | KATO B. Column Curves of Steel-concrete Composite Members[J]. Journal of Constructional Steel Research , 1996, 39 (2) : 121-135 |
| [9] | 周绪红, 刘界鹏, 张素梅. 圆钢管约束高强钢筋混凝土短柱的轴压力学性能[J]. 工程力学 , 2009, 26 (11) : 53-59 ZHOU Xu-hong, LIU Jie-peng, ZHANG Su-mei. Behavior of Circular Tubed Reinforced Concrete Stub Columns under Axial Compression[J]. Engineering Mechanics , 2009, 26 (11) : 53-59 |
| [10] | 程昌绪.外包钢筋混凝土加固柱正截面承载力理论分析[D].长沙:湖南大学, 2003. CHENG Chang-xu. Theoretical Analysis of Load Capacity of Reinforced Concrete Columns Strengthened with Reinforced Concrete Cover[D].Changsha:Hunan University, 2003. http://cdmd.cnki.com.cn/article/cdmd-10532-2004034316.htm |
| [11] | 王元丰, 朱海斌, 韩冰. 钢管混凝土受弯构件徐变的设计计算公式[J]. 公路交通科技 , 2007, 24 (4) : 105-107 WANG Yuan-feng, ZHU Hai-bin, HAN Bing. Design Method for Creep of Flexural Concrete Filled Steel Tubular Members[J]. Journal of Highway and Transportation Research and Development , 2007, 24 (4) : 105-107 |
| [12] | 刘威.钢管混凝土局部受压时的工作机理研究[D].福州:福州大学, 2005. LIU Wei. Research on Mechanism of Concrete-filled Steel Tubes Subjected to Local Compression[D]. Fuzhou:Fuzhou University, 2005. http://www.oalib.com/references/17684083 |
| [13] | 周志祥. 高等钢筋混凝土结构[M]. 北京: 人民交通出版社, 2002 : 26 -28. ZHOU Zhi-xiang. Advanced Reinforced Concrete Structures[M]. Beijing: China Communications Press, 2002 : 26 -28. |
| [14] | 韩林海, 冯九斌. 混凝土的本构关系模型及其在钢管混凝土数值分析中的应用[J]. 哈尔滨建筑大学学报 , 1995, 28 (5) : 26-31 HAI Lin-hai, FENG Jiu-bin. Constitutive Relations of Concrete and Its Applications in the Integral Analysis of Concrete Filled Steel Tube[J]. Journal of Harbin University of Architecture and Engineering , 1995, 28 (5) : 26-31 |
| [15] | 尧国皇.钢管混凝土构件在复杂受力状态下的工作机理研究[D].福州:福州大学, 2006. YAO Guo-huang. Research on Behaviour of Concrete-filled Steel Tubes Subjected to Complicated Loading States[D]. Fuzhou:Fuzhou University, 2006. http://cdmd.cnki.com.cn/article/cdmd-10386-2006162421.htm |
 2016, Vol. 33
2016, Vol. 33
