扩展功能
文章信息
- 罗媛, 颜东煌, 鲁乃唯, 汪勤用
- LUO Yuan, YAN Dong-huang, LU Nai-wei, WANG Qin-yong
- 随机车载下钢箱梁桥疲劳损伤概率模型
- Probabilistic Model of Fatigue Damage in Steel Box-girder Bridge Subject to Stochastic Vehicle Loads
- 公路交通科技, 2016, 33(10): 81-87
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 81-87
- 10.3969/j.issn.1002-0268.2016.10.013
-
文章历史
- 收稿日期: 2015-09-14
2. 东南大学 土木工程学院, 江苏 南京 210096
2. School of Civil Engineering, Southeast University, Nanjing Jiangsu 210096, China
钢箱梁具有较好的力学行为与经济性能,常被用于大跨度桥梁的主梁结构。近年来,美国I-35桥梁与国内诸多钢箱梁桥的疲劳安全事故引起了国际桥梁界的高度重视[1]。国外的钢桥疲劳设计规范相对较为完善,具有疲劳荷载谱和典型疲劳车辆[2],然而我国公路桥梁疲劳设计规范尚未完善。随着我国重载车辆的不断增加,车载下既有钢箱梁桥的疲劳安全问题日益突出[3]。由于车型和车辆等参数的随机性,车载下桥梁的疲劳应力为随机过程,桥梁的疲劳破坏为概率事件。随机车载下钢箱梁桥的疲劳损伤概率分析是评估该类结构安全性的一项重要内容。
由于钢桥疲劳损伤概率分析需要大量的疲劳应力数据,目前国内外学者普遍采用基于长期健康监测系统(SHMS)的疲劳应力数据[4-5]。基于SHMS的疲劳应力概率模型具有一定的可靠性与精确性,然而,SHMS方法在经济性与适用范围方面有一定的局限性。除此之外,有限元数值模拟方法和室内疲劳模型试验是获取疲劳应力的常用方法。Zhang等[6]分析了车速和路面平整度对疲劳损伤的影响。王春生[7]等通过无损探测信息和断裂力学方法对钢桥的疲劳性能进行研究并建立了概率模型。目前,国内外学者普遍采用典型疲劳车辆加载至桥梁有限元的方法获取疲劳应力谱[8],但是确定性的疲劳车辆难以建立疲劳应力概率模型。随机车流模型包含了车辆多参数的概率统计特征,可用于公路桥梁疲劳应力分析。然而,此方面的研究工作较为缺乏[9-10]。
本文将具有确定性参数的典型疲劳车辆模型改进为随机疲劳车流模型,采用小样本车辆轴重与等效疲劳应力数据拟合响应面的方法解决车流作用下桥梁有限元应力时程分析耗时过长的问题,提出钢箱梁顶板-U肋疲劳损伤概率建模方法。最后,将疲劳损伤概率模型应用于可靠度评估领域,揭示车流参数对结构疲劳可靠指标的影响规律。
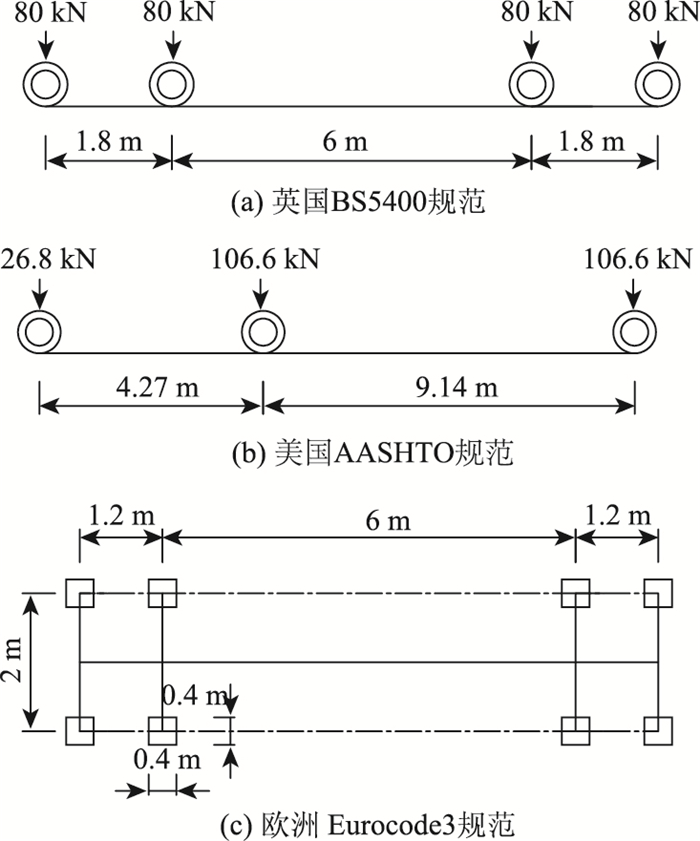
1 随机疲劳车流模型典型疲劳车辆是根据等效疲劳损伤原理,将统计车辆的疲劳损伤等效为某个固定的车辆对桥梁产生的疲劳损伤[11]。图 1给出了BS5400,AASHTO和Eurocode3等规范推荐的典型疲劳车辆模型。
|
| 图 1 国外设计规范中的典型疲劳车辆 Fig. 1 Typical fatigue trucks in foreign design specifications |
| |
图 1中,英国和美国规范车辆前轴为单轮,其他车轴均为双轮,欧洲规范的车辆每个轴重为120 kN。我国桥梁规范建议采用总重为550 kN的标准车辆,但未明确规定车辆形式。我国《正交异性钢桥面系统的设计和维护指南》建议对正交异性钢桥面板的疲劳设计采用车辆轴重为50,100,90 kN和90 kN的4轴疲劳车辆。上述典型疲劳车辆均为确定形式的荷载,可获取桥梁结构疲劳损伤值,但在概率损伤评估中的应用受到限制。
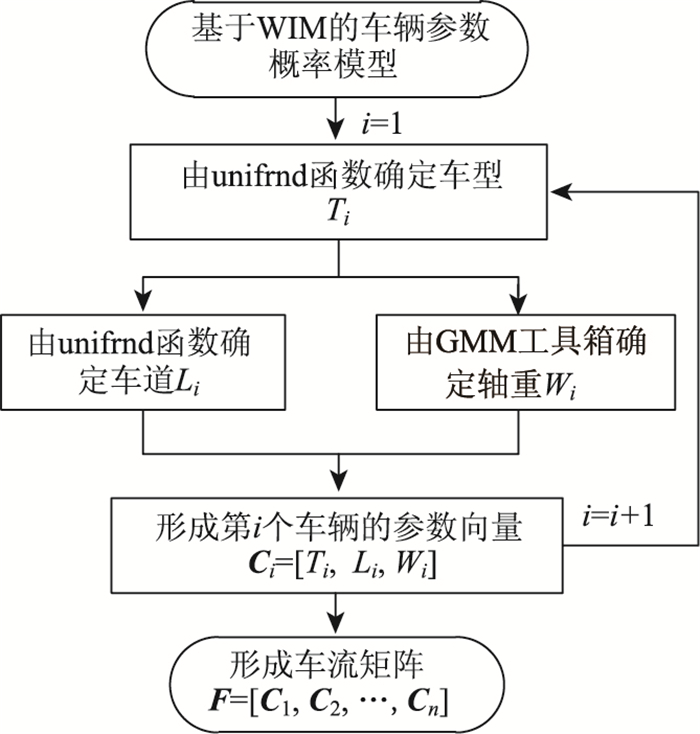
随机车流模型是一种将车辆多个参数,如车型、车重、车距和车速等,取为随机变量,采用一定的抽样方法生成时域车流荷载[12]。目前,随机车流主要应用于桥梁的动力响应分析。由于随机车流模型的车流参数是平稳随机过程,单个车辆是随机变量,可用于分析具有一定交通流量特征情况下桥梁的疲劳损伤概率。由于桥梁疲劳损伤为局部损伤,影响线范围较小[13],因此随机车流的5个随机变量对桥梁疲劳损伤的影响程度不同。一般认为,在随机疲劳车辆模型中可忽略车距、车速两个参数的变异性,仅采用车型、车重和车道这3个参数作为随机变量。在Matlab软件平台,采用Monte-Carlo抽样方法生成随机车流的步骤如图 2所示。
|
| 图 2 基于Monte-Carlo的随机车流模拟流程 Fig. 2 Flowchart of stochastic traffic flow simulation based on Monte-Carlo method |
| |
图 2中,车辆多参数概率模型由动态称重(WIM)监测数据得出;unifrnd函数与gmm函数分别是Matlab软件的函数库,分别表示均匀分布概率密度函数和高斯混合模型(GMM)概率密度函数;Monte-Carlo抽样得出的车辆矩阵Ci是由车道Li、车重Wi和车型Ti等3个参数形成的向量,最终循环抽样形成车辆参数矩阵F。
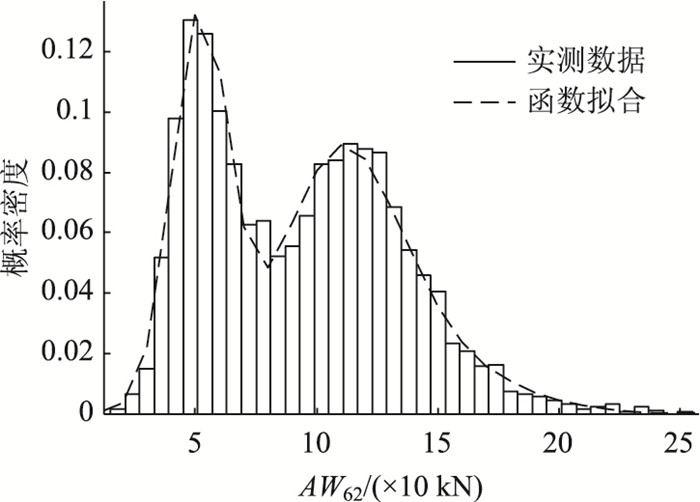
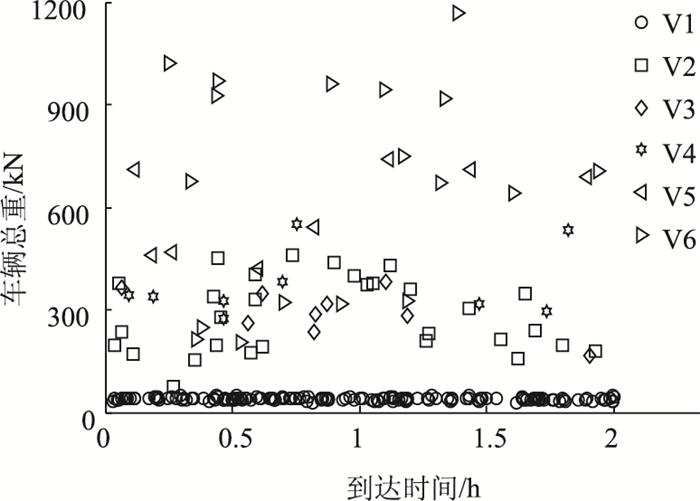
某高速公路WIM系统的车辆车型与车道统计参数如表 1所示。表 1中的车辆统计数据已经排除车重小于30 kN的小型车。采用GMM拟合的AW62轴重如图 3所示。根据图 2所示随机车流模拟步骤建立的随机疲劳车流样本如图 4所示。
| 车型 | 描述 | 占有率/% | ||
| 车型 | 行车道 | 超车道 | ||
| V1 | 2轴轻货车 | 34.64 | 36.64 | 63.36 |
| V2 | 2轴重型货车 | 26.12 | 84.58 | 15.42 |
| V3 | 3轴重型货车 | 8.58 | 91.08 | 8.92 |
| V4 | 4轴重型货车 | 10.24 | 96.42 | 3.58 |
| V5 | 5轴重型货车 | 4.93 | 92.60 | 7.40 |
| V6 | 6轴重型货车 | 15.49 | 98.08 | 1.92 |
|
| 图 3 AW62轴重概率密度分布 Fig. 3 PDD of axle weight AW62 |
| |
|
| 图 4 随机疲劳车流样本 Fig. 4 A stochastic fatigue traffic flow sample |
| |
图 4所示随机车流样本是将表 1和图 3所示概率统计数据代入图 2所示流程图,然后将矩阵F以图形的形式表示出来。随机疲劳车流模型的建立为下文桥梁疲劳损伤概率分析提供了有利条件。
2 桥梁疲劳损伤概率分析方法典型疲劳车辆作用下桥梁疲劳损伤的常用数值分析主要有3个步骤:首先,将疲劳车辆与桥梁有限元模型结合,提取局部应力时程曲线;其次,采用雨流计数方法提取应力循环;最后,针对结构构造细节选取合适的S-N强度曲线,由Palmgren-Miner线性累积损伤准则计算疲劳损伤。若采用上述方法计算随机疲劳车流作用下桥梁的疲劳损伤,则需大量的有限元计算,加之考虑桥梁构造细节的复杂有限元模型单元数量,无法直接实现疲劳应力损伤分析。此外,车流模型中参数有不同的分布类型,疲劳损伤的概率密度函数较为复杂,不能采用单一分布函数拟合。
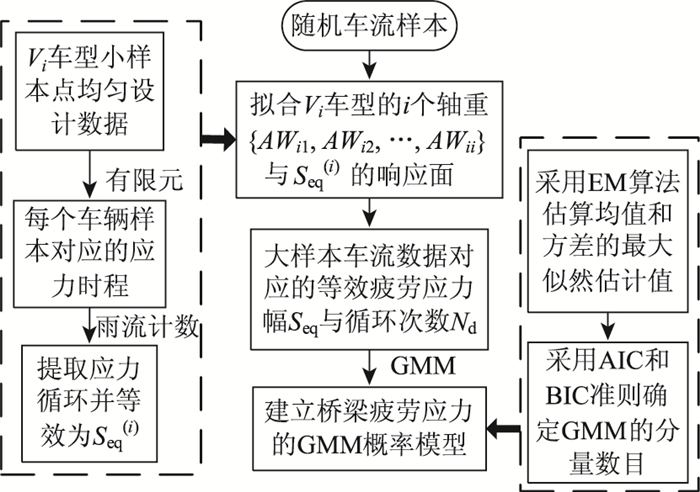
针对上述有限元计算耗时问题,本文在试验设计中采用常响应面方法(RSM)来拟合车辆参数与结构疲劳应力的函数关系,以小样本有限元分析数据反映出大量车流作用下的结构疲劳应力。针对复杂的疲劳损伤概率分布问题,本文采用多参数GMM模型建立疲劳损伤概率模型。整体分析框架如图 5所示。
|
| 图 5 疲劳应力概率分析流程 Fig. 5 Probability analysis process of fatigue stress |
| |
图 5中,AWi1为第Vi种车型的第1个轴重,EM是最大期望值的简称,AIC和BIC分别为信息统计学中的赤池准则和贝叶斯准则。其中,轴重与Seq的响应面关系,以及疲劳应力的GMM模型是该流程图中的关键步骤。
响应面方法的核心内容是采用一系列样本点数据拟合真实的结构响应[14]。通常采用的二次序列响应面方法能够反映出函数的非线性关系,较Taylor展开式精度高。对于车型Vi的车辆,则有i个轴重为随机变量,则响应面的待定系数为2i+1个,需要2i+1个以上的样本点确定不含交叉项的二次序列响应面表达式[14]:
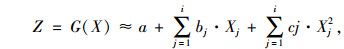
|
(1) |
式中, X为随机变量,本文中指每个车型的轴重; a, b, c均为待定系数。值得说明的是,每种车型Vi的响应面函数仅需要2i+1次有限元计算就可建立该车型的响应面函数。
在采用响应面函数求得大量车流作用下结构的疲劳应力幅之后,基于EM算法、BIC、AIC准则建立疲劳应力的最优GMM概率模型。GMM概率密度函数表达式为[15]:
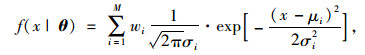
|
(2) |
式中, x在本文中为疲劳应力幅变量,θ为与μ和σ相关的GMM的统计参数向量; μi和σi分别为第i个均值和标准差; M为高斯模型的参数数量。EM算法主要分为E步骤和M步骤:E步骤是利用当前概率分布参数的估计值,求总体数据的对数函数的条件期望值;M步骤对上述期望值求极大似然估计。AIC和BIC准则可参考文献[15]。
3 钢箱梁桥的疲劳损伤概率分析车载作用下钢箱梁桥的疲劳损伤主要表现在顶板-U肋位置[16]。欧洲Eurocode3规范给出顶板-U肋处的细节分类为71,对应的强度系数分别为KC=7.16×1011, KD=1.90×1015。S-N强度曲线表达式为[15]
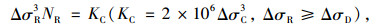
|
(3) |
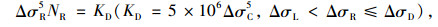
|
(4) |
式中, σD和ΔσL应分别为常幅疲劳极限和疲劳截止限; NR为循环次数。当应力幅ΔσR>ΔσD时,结构细节疲劳强度系数为KC;当ΔσR < ΔσD时,疲劳强度系数为KD。通过引入等效应力幅Seq,由S-N曲线和线性累积损伤准则可得到[17]:
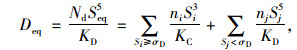
|
(5) |
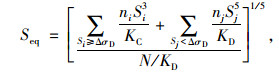
|
(6) |
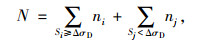
|
(7) |
式中,ni为Si≥ΔσD的应力循环次数; nj为Sj<ΔσD的应力循环次数; Deq为等效累积损伤。
某钢箱梁结构的顶板-U肋构造如表 2所示,车轮作用下其疲劳失效模式主要有焊趾开裂和焊跟开裂。采用ANSYS的Shell63单元建立标准梁段有限元模型如图 6所示。
| U肋厚 | 顶板厚 | 上口宽 | 下口宽 | 高度 | 间距 |
| 8 | 300 | 300 | 170 | 280 | 600 |

|
| 图 6 钢箱梁有限元模型 Fig. 6 Finite element model of steel box girder |
| |
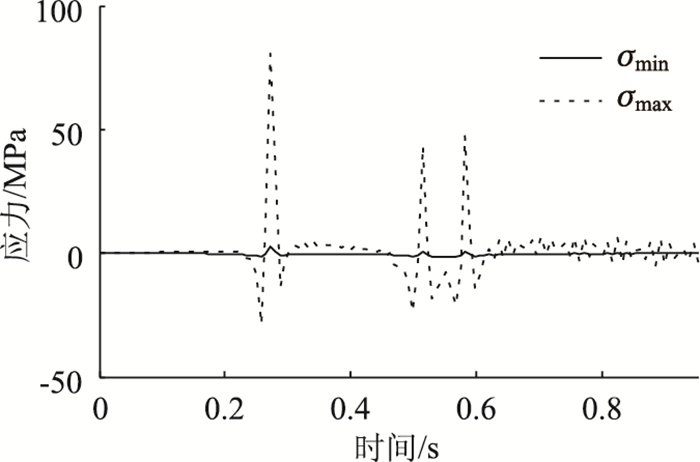
考虑到铺装层厚度对车辆轮胎着地面积的影响,轮胎呈45°扩展至桥面板,修正后的轮胎着地面积前轮为43.4 cm×33.4 cm,后轮为73.4 cm×33.4 cm。分别取V3车型总重最小车辆和总重最大车辆为代表车辆,以20 m/s的速度通过一块标准梁段,顶板-U肋处的应力时程曲线如图 7所示。
|
| 图 7 V3车型通过钢箱梁时顶板-U肋处的应力响应时程图 Fig. 7 Stress-time curves of rib-to-deck of steel box girder under V3 vehicle load |
| |
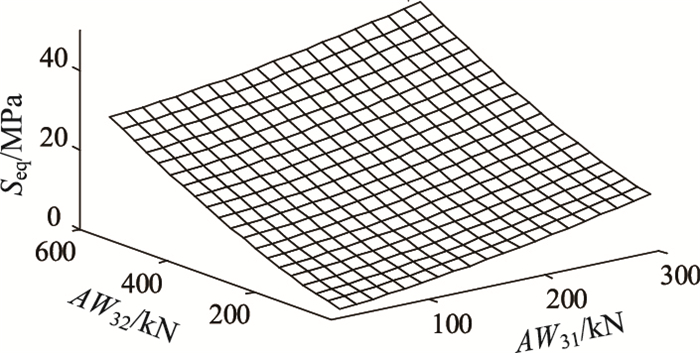
图 7中σmin和σmax分别为总重最小车辆和总重最大车辆通过一块钢箱梁时顶板-U肋处的应力时程曲线。该时程曲线由有限元的瞬态分析得到,首先根据车辆移动速度定义每个轴载(均布荷载)到达每个单元的时间点,然后定义车辆在桥面板移动的荷载步,最后通过瞬态分布得出钢箱梁关键点位置的应力时程曲线。由图 7可以看出,该应力时程曲线有明显的3个峰值,分别对应3个车轴通过关注点位置。将上述时程曲线通过雨流计数和式(5)~(7)的等效应力幅值处理可得到Seq。通过7个车辆样本的计算可由式(1)拟合出Seq与AW31, AW32的响应面,如图 8所示。
|
| 图 8 V3车型轴重对应Seq的响应面 Fig. 8 Response surface of Seq corresponding to axle weight of V3 |
| |
每种车型均对应一个响应面函数,将车流样本中的车型对号入座至每个响应面函数,则可得到车流样本作用下钢箱梁顶板-U肋的等效应力幅Seq。根据响应面算法的要求,本算例所采用的3轴车型对应的样本点数量为7个,6轴车型对应的样本点数量为13个,全部车型对应的样本点数为50个。以V3车型为例,在瞬态分析中共计118个荷载步,在配置为I5处理器和8G的电脑上每辆车通过如图 6所示的梁段所需计算时间约为43 s。因此,本算例车型对应的有限元计算时间约为36 min。本算例的100 d通行货车流量约为10万辆,若将每辆车当做一个样本点进行有限元分析,则需49 d计算时间, 采用本文所述响应面替代有限元计算则仅需36 min即可完成10万车辆的疲劳应力分析。由此可知, 响应面方法的引入解决了疲劳应力时程分析的耗时问题。
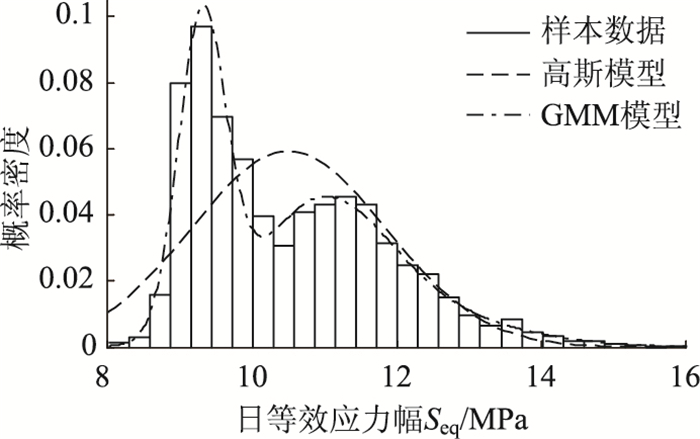
按照图 3所示GMM概率模型建立方法对Seq进行拟合,得到等效应力幅的概率密度曲线,如图 9所示。GMM的参数如表 3所示。
|
| 图 9 随机车流样本下行车道顶板-U肋的疲劳应力概率密度 Fig. 9 Fatigue stress probability density of rib-to-deck detail of driveway under random traffic flow samples |
| |
图 9中,等效应力幅Seq的概率密度图形近似有两个峰值,分别与图 3的轴重概率密度峰值对应,表示车辆的空载和满载状态。因此,Seq的概率密度函数采用两参数的GMM模型有较好的拟合效果。表 3中,GMM的两个均值参数近似于图 9的两个概率密度峰值。
钢箱梁桥顶板-U肋的疲劳损伤概率模型的建立表明了随机疲劳车辆模型的钢箱梁疲劳应力分析的可行性,以及GMM方法在疲劳应力概率拟合中的适用性。
4 基于疲劳损伤概率模型的可靠度评估随机疲劳车流作用下桥梁疲劳损伤模型的应用之一就是疲劳可靠度评估。根据线性累积损伤准则可建立考虑车流参数的疲劳损伤极限状态方程:

|
(8) |
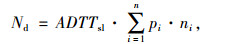
|
(9) |
式中, n为运营时间; w为轮迹横向分布系数; a为轴重的年增长系数; Δ为临界疲劳损伤; pi和ni分别为第i种车型的占有率和轮轴数量;ADTTsl为车辆的日通行量。该式中的随机变量X与4个参数有关,其概率统计数据如表 4所示。
针对式(5)所示显式功能函数,其非线性次数较高,且随机变量分布类型多样化,若采用传统的一次二阶矩阵法计算出的可靠度指标有较大的误差。
本文选取了计算精度较高的Monte Carlo抽样方法,结合MATLAB软件生成大量的服从正态分布函数、对数正态分布函数以及高斯混合分布函数的随机样本。
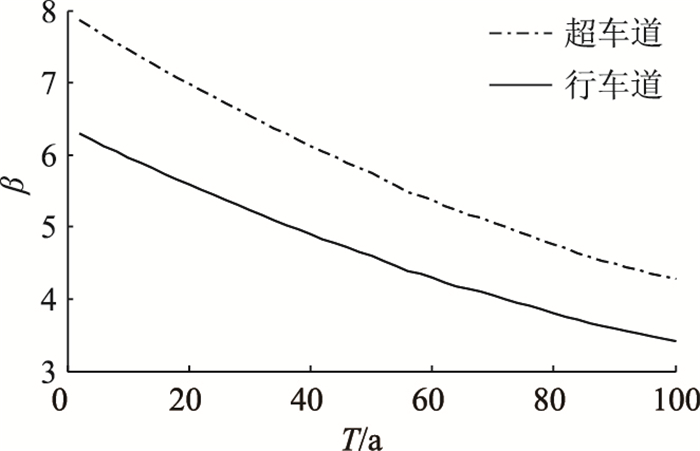
首先分析不考虑车辆轴重增长情况下行车道与超车道处顶板-U肋的疲劳可靠指标与失效概率的变化趋势,如图 10所示。
|
| 图 10 运营期内顶板-U肋细节疲劳可靠度变化趋势 Fig. 10 Change of fatigue reliability index of rib-to-deck detail during operation period |
| |
由图 10可知,第1年至第100年,行车道处顶板-U肋的疲劳可靠指标由6.29下降至3.42,对应的失效概率由1.6×10-10升高至3.15×10-4。随着桥梁服役时间的增长,行车道与超车道处顶板-U肋的疲劳可靠指标均呈下降趋势,行车道处的疲劳可靠指标低于超车道。由表 1所示行车道与超车道的车型占有比可知,约90%以上的3轴及以上货车均行驶于行车道,这使得行车道的疲劳损伤远大于超车道。
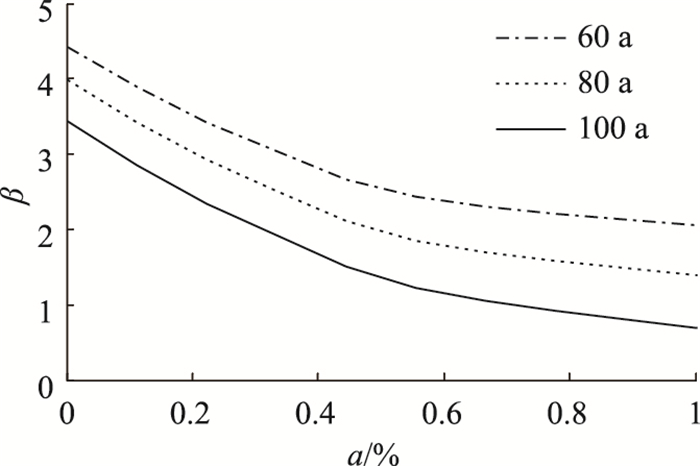
由于轴重与疲劳损伤呈指数关系,轴重的增长将对疲劳可靠度产生较大的影响。取轴重的年线性增长系数a的变化范围为0~1%,行车道处顶板-U肋的疲劳可靠指标的变化趋势如图 11所示。
|
| 图 11 车重增长系数对疲劳可靠指标的影响 Fig. 11 Influence of vehicle weight increase factor on fatigue reliability index |
| |
由图 11可知,在考虑车重增长的情况下,钢箱梁顶板-U肋的疲劳可靠指标迅速下降,车重年线性增长系数由0增长至1%时,第60年的疲劳可靠指标由4.43下降到2.01,第80年的疲劳可靠指标由3.98下降到1.30,第100年的疲劳可靠指标由3.42下降至0.72。随着桥梁服役时间的增长,疲劳可靠指标下降幅度增加。由此可知,桥梁的服役时间和车辆轴重增长导致焊接细节疲劳可靠性迅速降低。
5 结论本文将具有确定性参数的典型疲劳车辆模型改进为随机疲劳车流模型,采用小样本车辆轴重与等效疲劳应力数据拟合响应面的方法,解决了车流作用下桥梁有限元应力时程分析耗时过长的问题;提出钢箱梁桥顶板-U肋疲劳应力概率建模方法,最后将研究成果应用于某钢箱梁桥的疲劳可靠度评估,为桥梁的运营管理和交通限制提供理论依据。主要得出以下结论:
(1)随机疲劳车流模型包含了车辆的统计特征,在钢桥疲劳损伤概率分析与可靠度评估领域具有一定的应用前景。
(2)行车道重载车辆的较高占有率是导致钢箱梁顶板-U肋疲劳可靠指标远低于超车道处的重要原因。
(3)车辆轴重的增长致使钢箱梁疲劳可靠指标迅速降低,车重年线性增长系数由0增长至1%时,第100年的行车道顶板-U肋疲劳可靠指标由3.42下降至0.72。
随机疲劳车流模型中的车速和路面平整度等参数对疲劳损伤的影响有待考虑,此外,交通量与车重的增长系数有待结合长期监测数据进行验证。
| [1] | WOLCHUK R. Discussion of "I-35W Bridge Collapse" by S. Hao[J]. Journal of Bridge Engineering , 2011, 16 (4) : 570-571 |
| [2] | AASHTO LRFD SI-2007, AASHTO LRFD Bridge Design Specifications[S]. |
| [3] | 潘鹏, 李全旺, 周怡斌, 等. 某公路大桥车辆荷载调查与局部疲劳分析[J]. 土木工程学报 , 2011, 44 (5) : 94-100 PAN Peng, LI Quan-wang, ZHOU Yi-bin, et al. Vehicle Survey and Local Fatigue Analysis of a Highway Bridge[J]. China Civil Engineering Journal , 2011, 44 (5) : 94-100 |
| [4] | 陈志为. 基于健康监测系统的大跨多荷载桥梁的疲劳可靠度评估[J]. 工程力学 , 2014 (7) : 99-105 CHEN Zhi-wei. Fatigue Reliability Assessment of Multi-loading Suspension Bridges Based on SHMS[J]. Engineering Mechanics , 2014 (7) : 99-105 |
| [5] | CHEN Z W, XU Y L, WANG X M. SHMS-based Fatigue Reliability Analysis of Multiloading Suspension Bridges[J]. Journal of Structural Engineering , 2011, 138 (3) : 299-307 |
| [6] | ZHANG W, CAI C S. Fatigue Reliability Assessment for Existing Bridges Considering Vehicle Speed and Road Surface Conditions[J]. Journal of Bridge Engineering , 2011, 17 (3) : 443-453 |
| [7] | 王春生, 付炳宁, 张芹, 等. 正交异性钢桥面板足尺疲劳试验[J]. 中国公路学报 , 2013, 26 (2) : 69-76 WANG Chun-sheng, FU Bing-ning, ZHANG Qin, et al. Fatigue Test on Full-scale Orthotropic Steel Bridge Deck[J]. China Journal of Highway and Transport , 2013, 26 (2) : 69-76 |
| [8] | CASTILLO E, MENÉNDEZ J M, SÁNCHEZ-CAMBRONERO S, et al. A hierarchical Optimization Problem:Estimating Traffic Flow Using Gamma Random Variables in a Bayesian Context[J]. Computers & Operations Research , 2014, 41 (41) : 240-251 |
| [9] | JABARI S E, LIU H X. A Stochastic Model of Traffic Flow:Theoretical Foundations[J]. Transportation Research Part B:Methodological , 2012, 46 (1) : 156-174 |
| [10] | CHEN S R, WU J. Modeling Stochastic Live Load for Long-span Bridge Based on Microscopic Traffic flow Simulation[J]. Computers & Structures , 2011, 89 (9/10) : 813-824 |
| [11] | 邵雨虹, 吕彭民. 九江长江大桥疲劳车辆荷载谱[J]. 长安大学学报:自然科学版 , 2015, 35 (5) : 50-56 SHAO Yu-hong, LÜ Peng-min. Fatigue load spectrum for Jiujiang Yangtze River Bridge[J]. Journal of Chang'an University:Natural Science Edition , 2015, 35 (5) : 50-56 |
| [12] | 余志武, 朱红兵, 蒋丽忠, 等. 公路桥梁车辆荷载随机过程模型[J]. 中南大学学报:自然科学版 , 2011, 42 (10) : 3131-3135 YU Zhi-wu, ZHU Hong-bing, JIANG Li-zhong, et al. Vehicles Load Stochastic Process Model of Highway Bridges[J]. Journal of Central South University:Science and Technology Edition , 2011, 42 (10) : 3131-3135 |
| [13] | DENG Yang, LIU Yang, FENG Dong-ming. Monitoring Damage Evolution of Steel Strand Using Acoustic Emission Technique and Rate Process Theory[J]. Journal of Central South University , 2014, 21 (9) : 3692-3697 |
| [14] | KANG S C, KOH H M, CHOO J F. An Efficient Response Surface Method Using Moving Least Squares Approximation for Structural Reliability Analysis[J]. Probabilistic Engineering Mechanics , 2010, 25 (4) : 365-371 |
| [15] | 邓扬, 李爱群, 刘扬, 等. 钢桥疲劳荷载效应监测数据概率建模与疲劳可靠性分析方法[J]. 土木工程学报 , 2014, 47 (7) : 79-87 DENG Yang, LI Ai-qun, LIU Yang, et al. Probabilistic Modeling of Fatigue Loading Effects and Fatigue Reliability Evaluation for Steel Bridges Based on Monitored Data[J]. China Civil Engineering Journal , 2014, 47 (7) : 79-87 |
| [16] | 陈一馨, 吕彭民, 郭成军, 等. 钢桥面板U型肋与盖板焊缝构造细节疲劳性能评估[J]. 长安大学学报:自然科学版 , 2014, 34 (1) : 49-55 CHEN Yi-xin, LÜ Peng-min, GUO Cheng-jun, et al. Study on Fatigue Performance of Orthotropic Steel Bridge Deck U-rib and Cover Weld Structure[J]. Journal of Chang'an University:Natural Science Edition , 2014, 34 (1) : 49-55 |
| [17] | 鲁乃唯, 刘扬, 邓扬. 随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估[J]. 中南大学学报:自然科学版 , 2015, 46 (11) : 4300-4306 LU Nai-wei, LIU Yang, DENG Yang. Fatigue Damage and Life Assessment for Steel Decks of Suspension Bridge under Stochastic Traffic Flow[J]. Journal of Central South University:Science and Technology Edition , 2015, 46 (11) : 4300-4306 |
| [18] | 鲁乃唯.随机车流下悬索桥加劲梁动力响应概率模型与可靠度研究[D].长沙:长沙理工大学, 2015. LU Nai-wei. Probability Model of Dynamic Responses and Reliability Assessment for Stiffening Girders of Suspension Bridges under Random Traffic Flow[D]. Changsha:Changsha University of Science and Technology, 2015. http://cdmd.cnki.com.cn/article/cdmd-10536-1015393309.htm |
 2016, Vol. 33
2016, Vol. 33
