扩展功能
文章信息
- 马存明, 段青松, 廖海黎
- MA Cun-ming, DUAN Qing-song, LIAO Hai-li
- 积雪条件下箱型桥梁断面气动力特性数值分析和风洞试验
- Numerical Analysis and Wind Tunnel Test on Aerodynamic Characteristics of Box-shaped Bridge Section under Snow
- 公路交通科技, 2016, 33(10): 67-72
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 67-72
- 10.3969/j.issn.1002-0268.2016.10.011
-
文章历史
- 收稿日期: 2015-09-28
在降雪量较大地区,雪荷载是作用于结构的重要荷载,风荷载作用下积雪会发生迁移,从而在结构表面产生不均匀分布,积雪的不均匀分布可能会对结构气动力特性产生一定影响。目前风致雪漂移运动的研究方法主要有实地观测、风洞和水槽试验及数值模拟3种方法,其中数值模拟方法的应用最为广泛。
1993年Uematsu[1]首先以CFD预测结构周围的积雪分布并介绍了空气中漂移的雪的浓度输运方程以及积雪表面的侵蚀流量经验公式。科学家们随后接受了这种模拟方法,1998年Liston[2]通过控制边界附近的网格考虑了风雪运动中雪颗粒发生侵蚀沉积后的边界变化情况,并采用标准k-ε模型模拟了湍流;2004年Beyers[3]在前人的基础上尝试在数值模拟中考虑更多的影响因素;Sundsbo[4]等人对栏栅周围的积雪进行了数值模拟;2011年Tominaga[5]总结前人的数值模拟方法并提出新的方法。在国内,周暄毅、莫华美等人也通过FLUENT对风致雪漂移运动进行了数值模拟。
但是,上述学者对风致雪漂移运动的研究目前主要集中于建筑结构,对桥面积雪的不均匀分布研究较少;同时,目前对桥梁空气动力影响因素的研究一般集中于地震荷载、风荷载等,同时考虑风荷载和雪荷载的研究较少,并且规范中对于积雪分布的规定具有很大的局限性。桥面积雪由于风的作用会产生不均匀分布,积雪形状的变化会引起桥梁主梁周围流场的改变,进而引起其气动力特性的改变。本文以降雪量较大的内蒙古的某斜拉桥为例,首先通过FLUENT数值模拟不同风速下桥面积雪的不均匀分布;其次,通过风洞试验研究积雪的不均匀分布对桥梁主梁三分力系数、涡激振动性能以及颤振导数的影响,对降雪量较大地区的桥梁运行的舒适性和安全性有一定的意义。
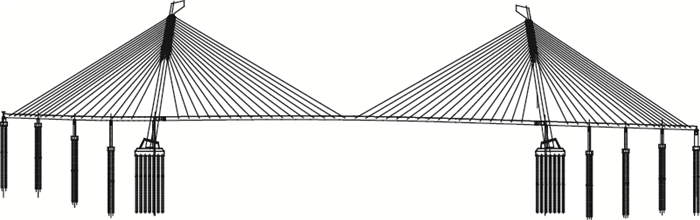
1 研究方法鄂尔多斯市位于内蒙古自治区,冬季气温偏低,降雪量较大。乌兰木伦河4号景观大桥位于该市康巴什新区,主桥边跨内布置辅助墩,主桥为跨径(40+42+42+51)m边跨+450 m中跨+(51+42+42+40)m边跨跨径布置的双斜塔斜拉桥(见图 1)。主跨大部分采用钢箱梁结构,边跨采用预应力混凝土箱梁结构,梁高均为3 m,主梁宽为37 m,见图 2。
|
| 图 1 总体布置图 Fig. 1 General arrangement |
| |

|
| 图 2 主梁截面图(单位:mm) Fig. 2 Main girder cross-section (unit: mm) |
| |
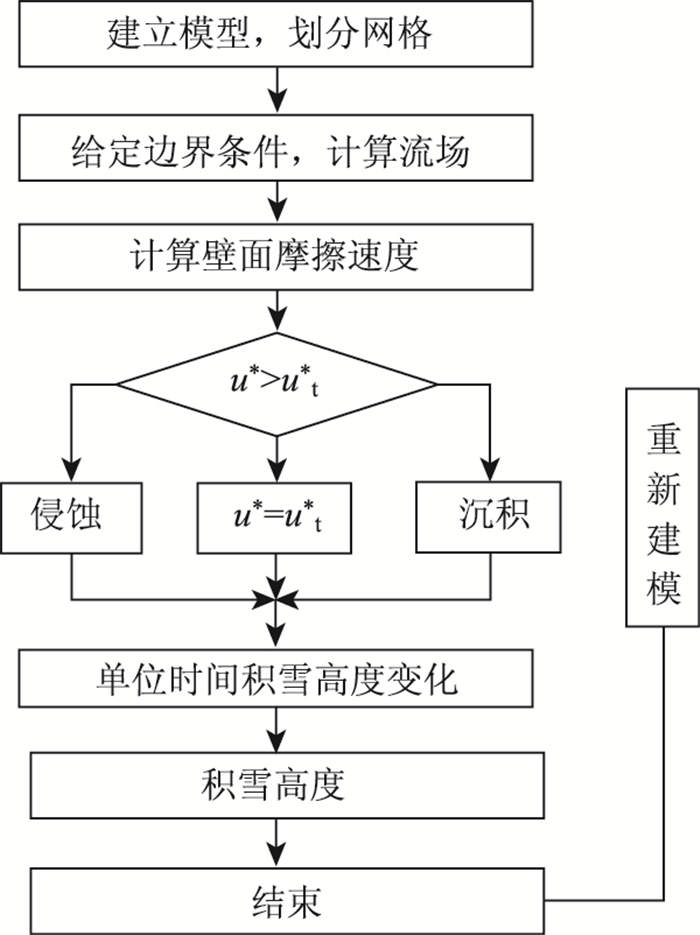
首先,通过FLUENT模拟不同风速下桥面积雪的不均匀分布。基于欧拉法考虑变形的重新建模方法,根据两相流理论知识、风致雪漂移的力学机理,求解流场以及雪的体积分数。同时根据经验公式得到一段时间后积雪形状后再重新建模,最终得到桥面积雪的不均匀分布形状,具体计算流程如图 3所示。
|
| 图 3 风致雪漂移数值模拟计算流程图 Fig. 3 Flowchart of numerical simulation of snow-drift |
| |
其次,在考虑10,15,20 m/s共3种不同风速时桥面积雪不均匀分布的基础上,采用塑料板模拟桥面积雪分布形状,置于桥梁表面,分析桥面积雪形状引起的主梁三分力系数、涡振性能、颤振导数等的变化。
2 风致雪漂移的数值模拟本文拟采用欧拉-欧拉方法,假设空气和雪均为连续相并且二者的关系为单相耦合,即只考虑空气使雪沉积、侵蚀,不考虑雪对空气的影响,通过求解空气、雪的控制方程实现风致雪漂移的数值模拟。本节中设定的条件为数值计算的基本条件,在此条件下进行风致雪漂移运动的非定常计算。
2.1 控制方程[6]数值模拟时采用Mixture混合模型,该模型通过求解空气、雪的控制方程实现风致雪漂移的数值模拟,具体方程此处不再赘述。同时,选用标准k-ε湍流模型,近壁面采用壁面函数模拟壁面附近复杂的流动现象。
2.2 积雪的侵蚀与沉积风致雪漂移过程中雪的沉积与侵蚀采用Naaim[7]提出的经验公式进行数值判断,当气流经过积雪面时会产生剪切力,剪切力是影响雪颗粒会发生沉积与侵蚀的重要因素。由于剪切力与摩擦速度的平方成正比,由此,雪的沉积与侵蚀主要通过摩擦速度大小来判断:当壁面摩擦速度大于阀值摩擦速度时,积雪发生侵蚀,侵蚀量由式(1)计算;当壁面摩擦速度小于阀值摩擦速度时,积雪发生沉积,沉积量由式(2)计算。
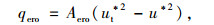
|
(1) |
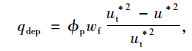
|
(2) |
式中,Aero为常系数,其值取7e-4;wf为雪的沉降速度,取0.2 m/s;u*为壁面摩擦速度,单位为m/s;ut*为阀值摩擦速度,取0.15 m/s;ϕp为雪的质量浓度,ϕp=ρp f,f为雪的体积分数,ρp为雪的密度;
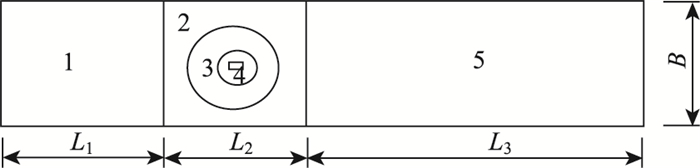
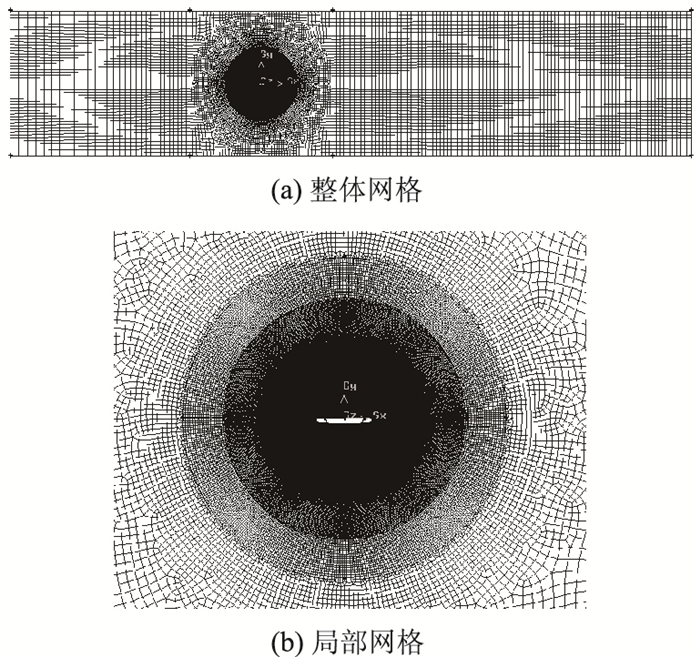
2.3 CFD模型 2.3.1 几何建模及网格划分采用二维分析模型,缩尺比为1:50,具体的区域划分示意图参见图 4,网格划分见图 5。二维计算流域取为38 m×8 m,区域1和区域5采用结构性网格,区域2~区域4采用Size Function函数控制划分,区域4到区域2网格尺寸从最小尺寸0.01 m到最大尺寸0.2 m,且满足y+值要求,网格总数约为15万左右。
|
| 图 4 计算区域划分示意图 Fig. 4 Schematic diagram of calculation region division |
| |
|
| 图 5 网格划分 Fig. 5 Meshing |
| |
图中,设定桥梁长为L,宽为H,取L1=10L,L2=8L,L3=20L,B=8L。
2.3.2 边界条件入口处,空气相和雪相采用速度入口边界条件,速度剖面按指数律形式分布,粗糙度系数α取为0.1;入流面处给定的湍流动能和湍流耗散率采用日本AIJ规范中的公式[8],雪相的入口边界条件考虑了悬移层和跃移层不同雪相的浓度分布,具体公式参照Pomeroy & Gray[9]和Pomeroy & Male[10]。
出口处为压力出口边界条件。积雪面为无滑移的壁面边界条件,雪面粗糙高度取为0.000 5 m;立方体壁面为无滑移壁面边界条件;计算域顶部为自由滑移壁面条件。
雪荷载密度取150 kg/m3,雪颗粒的沉降速度取0.2 m/s[11-12],雪颗粒的阀值摩擦速度取0.15 m/s,控制方程迭代收敛标准为均方根残差10-6。
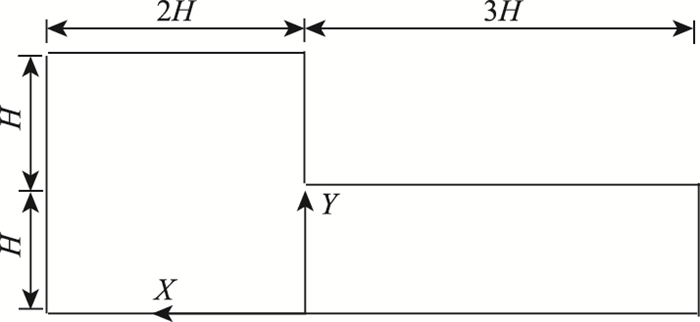
2.4 算例验证为了验证上述计算方法的准确性,本文以Tsuchiya的实测模型为例进行分析,并将结果与实测结果进行了对比。如图 6所示,H=0.9 m,低屋盖为迎风向,采用结构化网格划分计算区域,对结构附近网格加密,最小尺寸取为0.01 m,周边计算域选用稀疏网格,网格总数140 000左右。入口处速度取参考高度处0.9 m为7.4 m/s,其余边界条件参照2.3.2节选取。
|
| 图 6 高低屋面结构图 Fig. 6 High-low roof structure |
| |
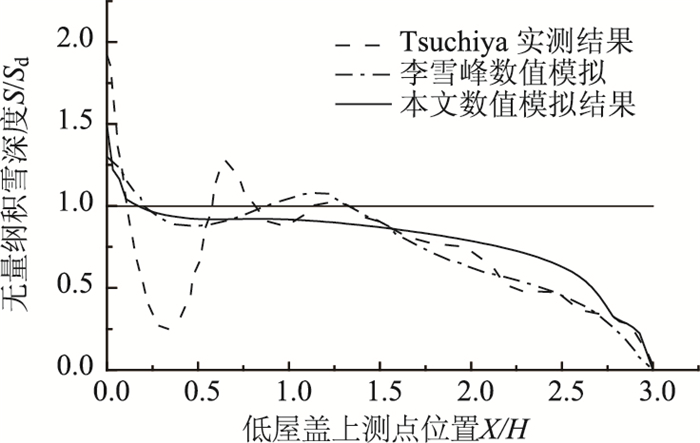
图 7给出了经过3次重新建模计算,即20 d以后的低屋盖表面风致雪漂移运动的数值模拟结果,采用的坐标系统如图 6所示。其中横坐标为低屋盖长度3H采用高度H无量纲化,并取绝对值的结果;竖向坐标为根据初始积雪厚度Sd(0.2 m)进行无量纲化的结果。
|
| 图 7 数值模拟结果对比 Fig. 7 Contrast of numerical simulation results |
| |
经对比分析,本文模拟结果与李雪峰数值模拟结果基本一致,而在高屋盖附近的低屋盖测点处的结果与Tsuchiya实测结果有一定的差距。Tsuchiya实测结果显示:在高屋盖附近,低屋盖表面积雪发生了很大程度的侵蚀,而数值模拟的侵蚀作用比较小;同时,实测结果中有出现积雪的沉积,数值模拟结果也未出现。主要原因是数值模拟的条件相对理想,同时实测过程中的风向、温度等条件并不是一直保持不变的,雪颗粒的受力也因此而随时间发生变化,不能达到数值模拟过程中的理想状态。
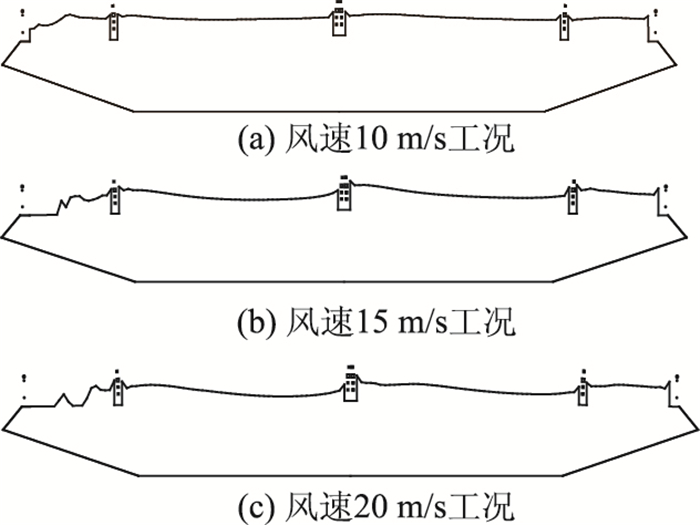
2.5 桥面风致雪漂移的数值模拟结果图 8中给出了桥面有积雪的结构坐标示意图,y轴为主梁对称轴,为根据初始积雪高度无量纲的积雪深度。图 9给出了桥面积雪分布的数值模拟结果,其中计算风速值为缩尺模型对应的风速。

|
| 图 8 坐标示意图 Fig. 8 Coordinate system |
| |
|
| 图 9 桥面积雪分布示意图 Fig. 9 Schematic diagram of snow distribution on deck |
| |
计算结果表明,在尾流处由于壁面摩擦速度较小,但大于阀值摩擦速度,因此积雪侵蚀量较少;在桥面迎风处风速远远大于阀值摩擦速度,积雪的侵蚀量较大;随着风速沿桥面逐渐减小,侵蚀量也逐渐地减小,桥梁背风侧积雪侵蚀量明显比迎风侧侵蚀量小,在尾流处侵蚀量最小。由于栏杆的影响,其附近风速相对较小,而积雪的侵蚀量也较小。
同时,随着入口处速度的增大,壁面摩擦速度逐渐增大,桥面迎风处积雪侵蚀量逐渐增大。通过对比可知,不同风速引起的桥面积雪侵蚀量主要是在迎风处,不同风速工况下,迎风处积雪形状有一定的差异,入口处风速越大,桥梁迎风处积雪侵蚀量越大,如3个不同风速下,桥面积雪的无量纲深度(积雪厚度/初始积雪厚度)为0.3, 0, 0,而在桥面背风处变化相对较小。
3 积雪对主梁气动力特性的影响研究根据第2节中不同风速下桥面积雪的数值模拟结果,积雪形状采用塑料板制作并置于桥面,分析不同风速下积雪的形状变化对主梁气动力特性的影响,同时试验过程中考虑了积雪荷载质量的影响。试验在西南交通大学XNJD-1第二试验段中进行,该风洞建于1991年,是国内较早建成的单回流串联双试验段风洞,试验段断面为2.4 m×2.0 m的矩形,来流风速范围为0.5~45 m/s。
3.1 积雪对主梁三分力系数的影响主梁节段模型的几何缩尺比为1:50,模型长L=2.095 m,宽B=0.74 m,高H=0.062 m,主梁用红松木和层板制作,防撞护栏和风障按图纸尺寸采用塑料板整体雕刻制作(见图 10~图 11)。图 12给出了三分力系数的试验结果。

|
| 图 10 局部细节 Fig. 10 Local details |
| |

|
| 图 11 三分力试验照片 Fig. 11 Photo of three-component force test |
| |
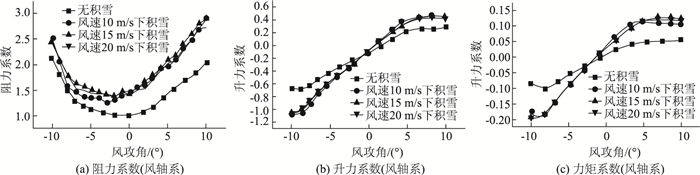
由试验结果(图 12)可知,考虑桥面积雪后,主梁的静力三分力系数绝对值均变大,正攻角下主梁的阻力系数比负攻角工况变化幅度大,随着攻角变为正,阻力系数增长幅度基本在15%左右。这可能是由于考虑积雪不均匀分布后,正攻角时气流在主梁下风侧产生更大的漩涡,而上风侧箱梁侧腹板处的气流变化不大,产生更大的压差,从而产生更大的阻力,升力系数和力矩系数增长幅度较阻力系数更大。考虑3种风速下的积雪后主梁的三分力系数变化基本不大,由此可见在一定风速范围内,积雪不均匀分布对主梁静力三分力系数的影响基本一致。
|
| 图 12 三分力系数对比 Fig. 12 Contrast of three-component coefficients |
| |
3.2 涡振特性
涡振起振风速较低,为降低模型的风速比,试验(图 13)采用较刚性的弹簧以提高模型的振动频率,根据《公路桥梁抗风设计规范》[9]桥梁的阻尼比取0.5%,表 1给出了具体的参数设置。
| 振型 | 频率/Hz | 风速比 | 阻尼比/% |
| 竖向 | 4.37 | 4.97 | 0.47 |
| 扭转 | 11.20 | 4.99 | 0.46 |

|
| 图 13 涡振试验照片 Fig. 13 Photo of vortex-induced vibration test |
| |
根据英国规范,当涡激振动的起振风速超过20 m/s时不考虑涡激振动舒适度的影响。我国许多大桥交通管理也规定,当风速超过25 m/s时大桥封闭。故本文只针对第一个涡振区(10~20 m/s)进行分析。
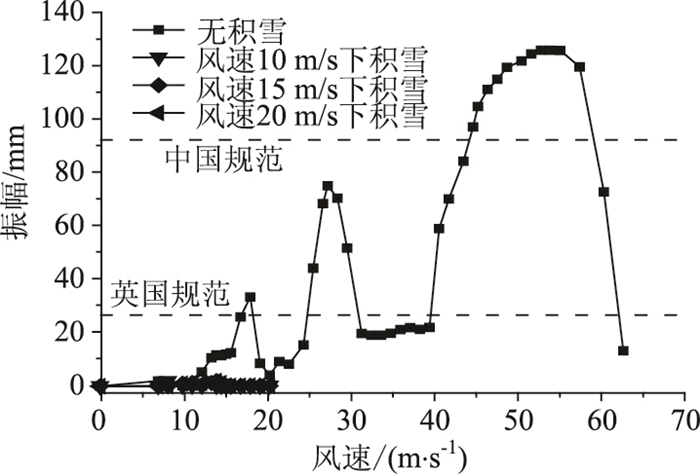
由图 14可知,由于积雪的影响,主梁+3°时的竖向涡激振动现象消失且积雪不均匀分布并未引起主梁的涡激振动。由此可见,对于本文的流线型钢箱梁而言,在一定风速下,积雪对主梁的涡激振动是有一定抑制作用且在一定的风速范围内,作用基本一致。
|
| 图 14 主梁竖向+3°攻角涡振结果 Fig. 14 Vertical vortex-induced vibration result at +3°attack angle of girder |
| |
3.3 颤振导数
颤振导数是表征断面气动自激力特征的一组函数,只要得到颤振导数,就可根据它计算同一形状断面在任意运动状态(微振动)中的气动自激力。本文中试验采用弹簧悬挂二元刚体节段模型,对攻角α=0°时主梁颤振导数进行试验。
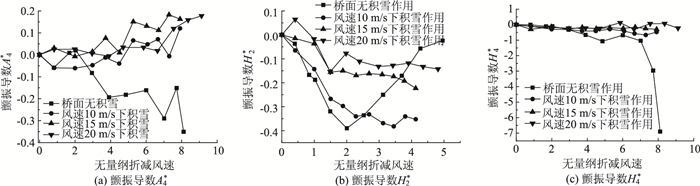
根据试验结果可知:H1*, A1*, H3*, A2*, A3*数值变化相对较小(如图 15所示,本文中只列出变化较大的颤振导数结果)。由于积雪作用,A4*曲线斜率由负变为正,且不同风速下的积雪形状影响较小;当无量纲折减风速增大到一定程度时,积雪影响下H2*逐渐趋于平缓;由于积雪影响,不同折减风速下的H4*基本保持不变。
|
| 图 15 颤振导数 Fig. 15 Flutter derivatives |
| |
由于积雪作用,由竖向运动位移引起的气动惯性和气动刚度对自激升力和扭矩的贡献由负变正;由扭转运动位移引起的气动惯性对自激扭矩的贡献减小;当折减风速增大到2左右时,由扭转运动速度引起的气动阻尼对自激升力的贡献变为负。
4 结论(1) 积雪的沉积侵蚀与壁面摩擦速度有紧密的联系,桥面背风侧积雪侵蚀量明显比迎风侧侵蚀量小,在尾流处侵蚀量最小。
(2) 由于积雪作用,主梁升力系数与扭矩系数曲线的斜率变大同时增幅在40%左右;阻力系数增大15%左右,且三分力系数变化趋势基本不变。
(3) 积雪作用下主梁在+3°时的竖向涡激振动消失且3个风速下的积雪的影响基本一致。
(4) 通过风洞试验分析发现H1*,A1*,H3*,A2*,A3*数值在考虑积雪作用前后变化相对较小,而对H2*,H4*,A4*影响较大。
| [1] | SATO T, UEMASTU T, NAKATA T, et al. Three Dimensional Numerical Simulation of Snowdrift[J]. Journal of Wind Engineering and Industrial Aerodynamics , 1993, 46/47 : 741-746 |
| [2] | LISTON G E, STURM M. A Snow Transport Model for Complex Terrain[J]. Journal of Glaciology , 1998, 44 (148) : 498-516 |
| [3] | BEYERS J H M, SUNDSBO P A, HARMS T M. Numerical Simulation of Three-Dimensional, Transient Snow Drifting Around a Cube[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2004, 92 (9) : 725-747 |
| [4] | SUNDSBO P A. Numerical Simulations of Wind Deflection Fins to Control Snow Accumulation in Building Steps[J]. Journal of Wind Engineering and Industrial Aerodynamics , 1998, 74/75/76 : 543-552 |
| [5] | TOMINAGA Y, OKAZE T, MOCHIDA A. CFD Modeling of Snowdrift Around a Building:An Overview of Models and Evaluation of a New Approach[J]. Journal of Building Environment , 2011, 46 (4) : 899-910 |
| [6] | 吴望一. 流体力学[M]. 北京: 北京大学出版社, 2000 . WU Wang-yi. Fluid Mechanics[M]. Beijing: Peking University Press, 2000 . |
| [7] | NAAIM M, NAAIM-BOUVET F, MARTINEZ H. Numerical Simulation of Drifting Snow:Erosion and Deposition Models[J]. Annals of glaciology , 1998, 26 : 191-196 |
| [8] | 日本建筑协会.房屋荷载建议[M].[S.l.]:日本建筑协会, 1995. Architectural Institute of Japan. Recommendations for Loads on Building[M].[S.l.]:Architectural Institute of Japan, 1995. |
| [9] | POMEROY J W, GRAY D M. Saltation of Snow[J]. Water Resources Research , 1990, 26 (7) : 1583-1594 |
| [10] | POMEROY J W, MALE D H. Steady-state Suspension of Snow[J]. Journal of Hydrology , 1992, 1/2/3/4 : 275-301 |
| [11] | 周晅毅, 顾明. 首都国际机场3号航站楼屋面雪荷载分布研究[J]. 同济大学学报 , 2008, 35 (9) : 1193-1196 ZHOU Xuan-yi, GU Ming. Study on Snow Loads on Roof of Terminal 3 of Beijing Capital International Airport[J]. Journal of Tongji University , 2008, 35 (9) : 1193-1196 |
| [12] | GAMBLE S L, KOCHANSKI W W, IRWIN P A. Finite Area Element Snow Loading Prediction-Applications and Advancements[J]. Journal of Wind Engineering and Industrial Aerodynamics , 1992, 42 (S1/S2/S3) : 1537-1548 |
 2016, Vol. 33
2016, Vol. 33
