扩展功能
文章信息
- 琚明杰, 刘世明, 刘永健
- JU Ming-jie, LIU Shi-ming, LIU Yong-jian
- 索力随机误差对组合梁无背索斜拉桥受力影响
- Influence of Random Deviation of Cable Tension Force on Stress State of Composite Girder Cable-stayed Bridge without Back-stay
- 公路交通科技, 2016, 33(10): 60-66
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(10): 60-66
- 10.3969/j.issn.1002-0268.2016.10.010
-
文章历史
- 收稿日期: 2015-06-05
2. 华北水利水电大学 土木与交通学院, 河南 郑州 450045;
3. 长安大学 旧桥检测与加固技术交通行业重点实验室, 陕西 西安 710064
2. School of Civil Engineering and Communications, North China University of Water Resources and Electric Power, Zhengzhou Henan 450045, China;
3. Key Laboratory for Bridge Detection and Reinforcement Technology of Ministry of Transport, Chang'an University, Xi'an Shaanxi 710064, China
在斜拉桥施工过程中,受现有施工技术水平的限制,不可避免存在一些施工误差,如结构自重[1]、弹性模量[2]、拉索张拉力[3]、制作安装偏差、混凝土收缩徐变[4]等,这些偏差将影响结构的应力、变形、极限承载力和可靠度[5-7]。在桥梁设计过程中,为简化计算分析,往往采用规范规定的材性、荷载、施工顺序[8]和设计图纸的截面参数、空间位置等[9],忽略或通过引入安全系数来考虑施工中存在的诸多不确定因素,这种确定性分析仅在结构体系变异比较小时才能得到较为接近实际的结果。曲塔曲梁无背索斜拉桥空间线形独特,结构受力复杂,文献[10]考虑施工误差的影响,通过确定性误差分析了各参数敏感性。从概率意义上把握结构空间力学行为,准确反映结构的力学本质及对结构可靠度的影响,有重要的理论意义和工程意义。
本文结合东莞水道桥的施工监控及相关科研工作,以拉索初拉力为随机变量,考察拉索初拉力变化对结构构件受力及可靠度的影响,为确定合理的斜拉索施工控制精度提供依据。
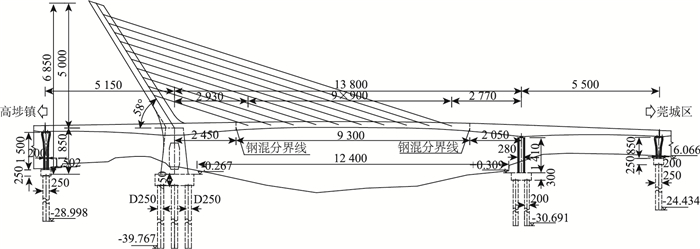
1 桥梁结构分析 1.1 桥梁概况东莞水道桥平面位于半径为800 m的圆曲线上,小桩号侧纵坡为1.68%,大桩号侧纵坡为-4%,竖曲线半径为2 000 m。采用塔梁墩固结体系无背索曲塔曲梁斜拉桥,跨径布置为(51.5+138+55)m[11]。桥梁立面、平面和桥塔处横断面如图 1~图 3所示。
|
| 图 1 桥梁立面图(单位:cm) Fig. 1 Elevation view of bridge (unit: cm) |
| |
|
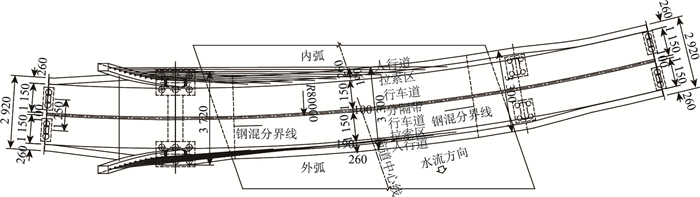
| 图 2 桥梁平面图(单位:cm) Fig. 2 Plan view of bridge (unit: cm) |
| |
|
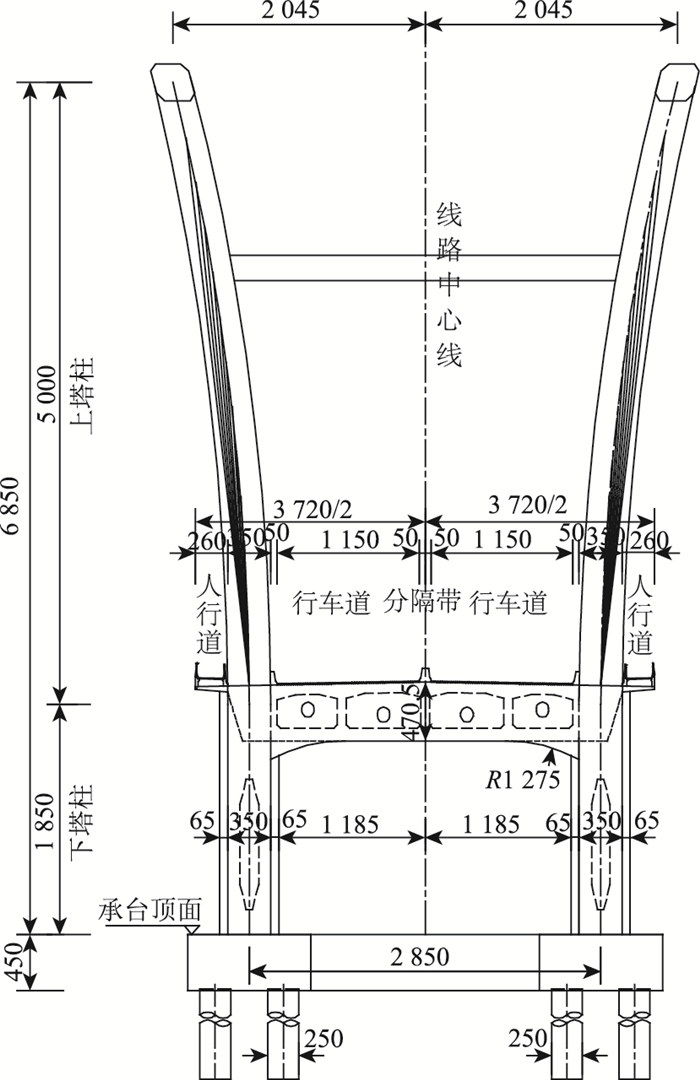
| 图 3 桥塔处横断面图(单位:cm) Fig. 3 Sectional view at pylon of bridge (unit: cm) |
| |
主塔位于车行道与人行道之间,每个主塔横桥向宽3~3.5 m,顺桥向宽4~5.5 m,主塔横桥向往外圆弧张开,顺桥向水平倾角为58°。上塔柱采用预应力钢箱混凝土结构,在内外钢箱内填充C50微膨胀混凝土,每个塔柱共13个节段,采用悬臂拼装施工。下塔柱为变截面空心普通钢筋混凝土结构。两塔柱间设置两道横向备用拉索,离桥面垂直距离分别为34.506, 31.894 m。横向备用拉索规格为GJ15-3,锚固于塔柱侧壁。
主梁采用钢混凝土混合梁,主跨中间一段93 m为钢箱梁,采用变截面梁高2.3~3.014 m,两端各设一个钢混结合段。边跨为变截面斜腹板混凝土梁,梁高2.3~4.5 m。桥面标准宽度为33 m,桥塔位置处加宽至37.2 m,55 m边跨桥宽由29.2 m变宽至33 m,51.5 m边跨桥宽由37.2 m变化至29.2 m。
拉索采用竖琴式双索面布置,钢梁上索距为9.0 m,拉索水平夹角为18°,拉索规格为GJ15-15,GJ15-19,GJ15-22,共计20根拉索,采用桥塔端张拉。
桥梁施工采用先梁后塔的施工方法,主梁承担自身重量和30%~40%的活载作用,拉索仅承担60%~70%的活载作用。
1.2 有限元模型考虑桥梁平弯、纵横坡、材料及主要施工过程,采用ANSYS有限元程序中的参数化设计语言APDL(ANSYS Parametric Design Language),建立了随机有限元空间分析模型。其中,主塔钢箱和混凝土、主梁、墩身、承台等均采用梁单元BEAM188模拟;拉索采用索单元LINK180模拟,并按Ernst公式对弹性模量进行修正;支座弹簧采用弹簧单元COMBIN14模拟,弹簧刚度按支座特性计算[12];拉索与主塔、主梁间连接采用连接单元MPC184模拟。模型共采用4种单元类型,24种材料属性,270个节点,266个单元。主要边界条件为主塔钢箱与混凝土部分采用共节点模拟,承台底部固结。建模过程中,对于非规则的BEAM188截面采用自定义截面;主塔、主梁内预应力钢筋采用等效荷载法模拟,普通钢筋采用调整材料弹性模量模拟;斜拉索初拉力采用初应变形式施加,以成桥索力为目标索力值,进行数次迭代计算得到。为提高计算效率,突出主要问题,考虑几何非线性影响,把施工阶段简化为21个,见表 1。随机有限元计算模型见图 4。

|
| 图 4 随机有限元计算模型 Fig. 4 Stochastic finite element model |
| |
| 施工阶段 | 主要工作内容 |
| 施工 阶段1 | 下部结构、主塔节段1、混凝土主梁及结合段施工凝土 |
| 施工 阶段2 | 两侧钢梁节段1对称施工 |
| 施工 阶段3 | 两侧钢梁节段2对称施工 |
| 施工 阶段4 | 两侧钢梁节段3对称施工 |
| 施工 阶段5 | 两侧钢梁节段4对称施工 |
| 施工 阶段6 | 大桩号侧钢梁节段5施工 |
| 施工 阶段7 | 合龙段施工 |
| 施工 阶段8 | 主塔节段2、3及拉索1施工 |
| 施工 阶段9 | 主塔节段4及拉索2施工 |
| 施工 阶段10 | 主塔节段5及拉索3施工 |
| 施工 阶段11 | 主塔节段6及拉索4施工 |
| 施工 阶段12 | 主塔节段7及拉索5施工 |
| 施工 阶段13 | 主塔节段8及拉索6施工 |
| 施工 阶段14 | 主塔节段9及拉索7施工 |
| 施工 阶段15 | 主塔节段10及拉索8施工 |
| 施工 阶段16 | 主塔节段11及拉索9施工 |
| 施工 阶段17 | 主塔节段12及拉索10施工 |
| 施工 阶段18 | 主塔节段13及桥面铺装施工 |
| 施工 阶段19 | 小桩号侧边跨移动荷载最不利布置 |
| 施工 阶段20 | 大桩号侧边跨移动荷载最不利布置 |
| 施工 阶段21 | 主跨移动荷载最不利布置 |
1.3 随机有限元可靠度分析流程
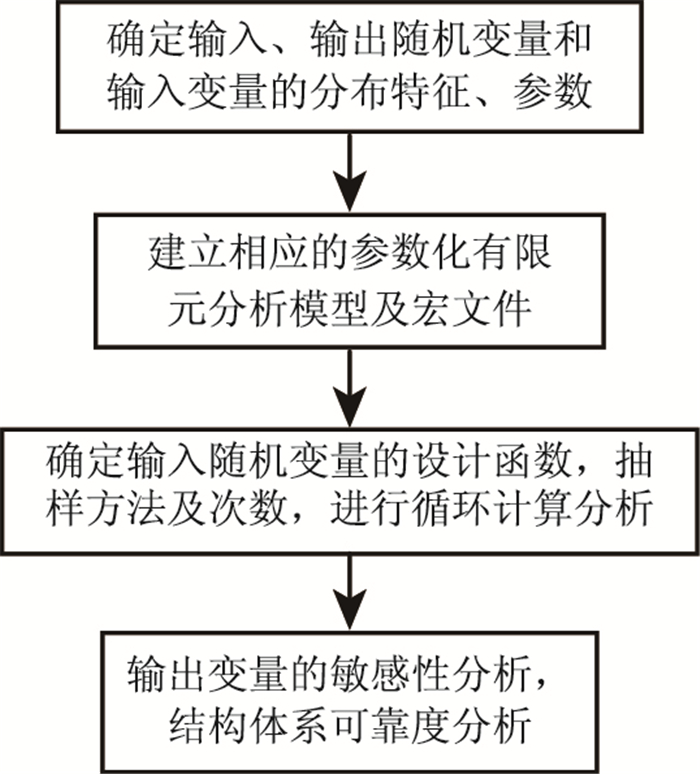
采用ANSYS有限元分析程序,进行随机有限元可靠度分析包括以下4步:
(1)根据研究对象性质、特点和侧重点,明确输入、输出随机变量,确定输入变量的分布特征及相关参数。
(2)在前处理模块中,基于以上输入、输出变量建立参数化的有限元分析模型,生成相应的宏文件。
(3)在可靠度设计模块中,确定随机输入变量的概率设计函数,随机变量的抽样方法及次数,进行随机有限元循环计算分析。
(4)在可靠度设计后处理模块中,获得输出变量的敏感性参数,确定结构体系可靠度指标。
分析流程如图 5所示。
|
| 图 5 随机有限元分析流程图 Fig. 5 Flowchart of stochastic finite element analysis |
| |
2 随机参数的选取 2.1 索力误差水平及分布参数
《公路斜拉桥实施细则》(JTG/T D65-01—2007)规定,斜拉索索力与设计的允许误差精度需满足设计要求,且不宜大于5%。钢绞线斜拉索索内各绞线索力误差宜控制在2%~8%。
斜拉索在张拉过程中往往会出现回缩,并且相邻拉索张拉会交互影响索力值大小,初始索力误差一般在5%左右,并且各拉索初拉力误差值在施工完成前并不确定,研究表明拉索初拉力误差满足正态分布[13],故选取拉索初拉力为输入随机变量,共20个随机变量,按2%,5%和8%共3个误差水平进行随机误差的影响分析。拉索初始索力值采用设计值,均值为0,标准差为对应的误差水平。取移动荷载下三跨主梁的跨中竖向位移、运营过程中三跨主梁的跨中、钢混结合段位置应力和位移、主塔节段3,5,7,9及塔顶位置的应力和位移为输出变量。
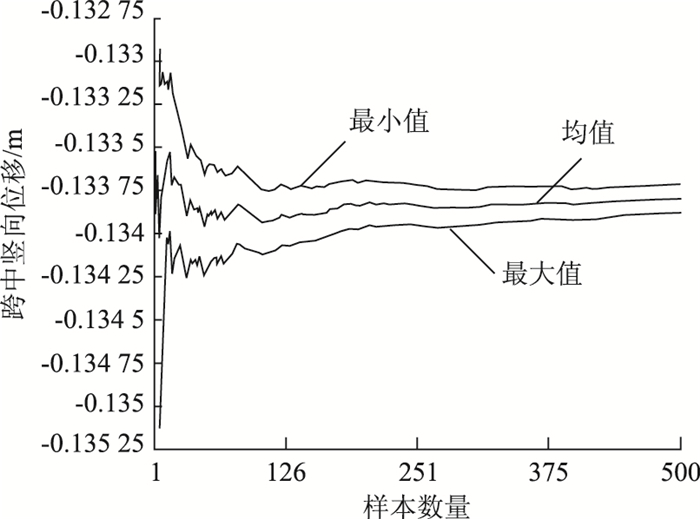
2.2 概率设计函数和抽样方法及次数因随机变量的个数比较多,概率设计函数宜选用蒙特卡罗方法,其抽样方法有直接抽样和拉丁超立方抽样两种[14]。因拉丁超立方抽样具有记忆功能,可以避免直接抽样数据点集中而导致仿真循环抽样的重复问题,比直接抽样法效率更高。研究表明在相同的精度范围内,拉丁超立方抽样次数为直接抽样法的60%~80%,故选用拉丁超立方抽样方法。随机抽样次数根据试算500次和2 000次,在相同工况下比较两种抽样次数下所得均值、标准差的差别不大,故选用抽样次数为500次,对应的可靠度精度为0.2%(与抽样次数互为导数)。主梁跨中的竖向位移均值随抽样次数的变化如图 6所示,图中从上往下3条曲线分别为主梁跨中竖向位移的最小值、均值和最大值,由图可知,当抽样次数达500次时,均值及变化量小,变化幅度稳定,抽样次数选取合理。
|
| 图 6 主跨跨中竖向位移随抽样次数的变化图 Fig. 6 Vertical deformation of mid-span of main span varying with sampling times |
| |
2.3 敏感性分析
(1)主梁应力、位移敏感性分析
在显著水平2.5%时,主梁典型位置处的应力、位移敏感参数及百分比见表 2、表 3。表中内侧指桥梁平曲线圆心侧,用字母N表示;外侧指背离圆心侧,用字母W表示。表中N9表示内侧9号拉索,W9表示为外侧9号拉索,拉索的编号从小桩号依次为1~10,其中敏感参数百分比带括号者为负相关,无括号者为正相关,以下同。
| 位置 | 第1敏感参数 | 第2敏感参数 | 第3敏感参数 | ||||
| 名称 | 百分比 | 名称 | 百分比 | 名称 | 百分比 | ||
| 小桩号 侧跨中 | 外侧下缘 | W9 | (10.38) | W10 | (9.93) | W5 | (9.04) |
| 内侧下缘 | N10 | (10.56) | N9 | (9.54) | N7 | (8.77) | |
| 小桩号 侧结合段 | 外侧上缘 | W3 | (12.39) | W4 | (10.83) | W2 | (10.39) |
| 内侧上缘 | N3 | (11.21) | N2 | (10.53) | N5 | (9.72) | |
| 外侧下缘 | N5 | 10.26 | N3 | 9.96 | N4 | 9.65 | |
| 内侧下缘 | W3 | 11.25 | W4 | 10.47 | W5 | 10.24 | |
| 大桩号 侧结合段 | 外侧上缘 | N7 | (11.1) | N5 | (10.84) | N6 | (10.39) |
| 内侧上缘 | W7 | (10.35) | W5 | (10.25) | W8 | (10.01) | |
| 外侧下缘 | W5 | 10.78 | W6 | 8.85 | N5 | 8.8 | |
| 内侧下缘 | N5 | 10.14 | W5 | 9.42 | N6 | 9.34 | |
| 大桩号 侧跨中 | 外侧下缘 | W5 | 8.46 | N6 | 7.96 | N7 | 7.83 |
| 内侧下缘 | W9 | 9.08 | W10 | 8.76 | W5 | 8.5 | |
由表 2可知,主梁的外侧上缘和内侧下缘应力的影响索号大致相同,小桩号侧跨中、大桩号侧结合段处主梁的外侧上缘和内侧下缘应力受内侧拉索初拉力影响较明显,而内侧上缘和外侧下缘应力受外侧拉索初拉力影响较明显,大桩号侧跨中、小桩号侧结合段处主梁应力与其相反。1号拉索初拉力对主梁整体的应力影响不明显; 5号拉索初拉力对主梁整体的应力影响较显著; 2~4号拉索初拉力对小桩号侧结合段应力影响明显; 6~8号拉索初拉力对大桩号侧结合段、大桩号侧跨中应力影响明显; 9~10号拉索初拉力对小桩号侧、大桩号侧跨中应力影响明显。
由表 3可知:5~7号拉索初拉力对主梁主跨跨中y、z方向的位移影响明显; 9~10号拉索初拉力对主梁边跨跨中z方向位移影响明显。
| 位置及方向 | 第1敏感参数 | 第2敏感参数 | 第3敏感参数 | ||||
| 名称 | 百分比 | 名称 | 百分比 | 名称 | 百分比 | ||
| 小桩号侧跨中 | z方向 | W10 | 8.88 | W9 | 8.79 | N10 | 8.1 |
| 主跨跨中 | y方向 | W7 | 10.52 | W6 | 9.28 | W5 | 8.98 |
| z方向 | W5 | 11.01 | N5 | 10.45 | N6 | 9.02 | |
| 大桩号侧跨中 | z方向 | W5 | (8.57) | W9 | (8.47) | W10 | (8.1) |
(2)主塔应力、位移敏感性分析
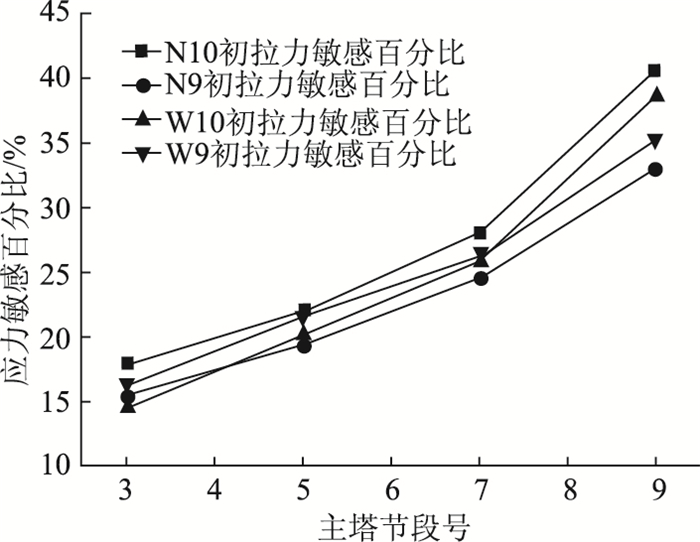
主塔应力受9~10号索初拉力影响较明显,主塔节段内侧上缘处应力敏感性百分比如图 7所示,随塔身高度的增加拉索敏感性百分比有所增加;相同主塔节段内侧上缘应力,N10拉索初拉力敏感性百分比均大于W10初拉力,W9拉索初拉力敏感性百分比均大于N9初拉力,其变化趋势一致。
|
| 图 7 主塔节段内侧上缘处应力敏感百分比图 Fig. 7 Curves of sensitivity percentage of stress at inside and upper of main pylon segment |
| |
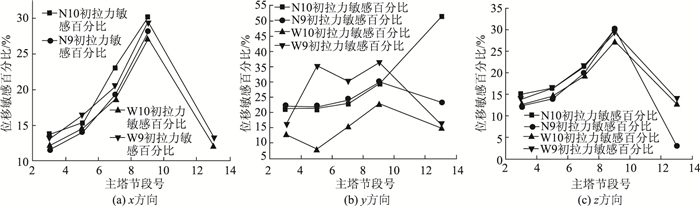
除3号节段、塔顶位置外,主塔位移受9~10号索初拉力影响较明显,主塔节段x,y,z方向敏感性百分比如图 8所示,随塔身高度的增加拉索敏感性百分比有所增加;相同主塔节段各方向位移,N10拉索初拉力敏感性百分比均大于W10初拉力,W9拉索初拉力敏感性百分比均大于N9初拉力,其变化趋势基本一致;内侧塔顶x、z方向位移敏感拉索分别为5号、6号索初拉力,外侧塔顶y方向位移敏感参数分别为1号、9号索初拉力。
|
| 图 8 主塔节段位移敏感百分比图 Fig. 8 Curves of sensitivity percentage of deformation of main pylon segment |
| |
(3)成桥索力敏感性分析
因本桥以主梁受力为主,拉索受力为辅,影响成桥阶段拉索应力的最敏感因素为自身的初拉力,敏感性百分比均在78%以上,N2,N4,N6,N7,W2,W3拉索应力只受自身初拉力影响,其他索力的影响可以忽略不计。
2.4 索力误差水平对结构应力、位移标准差的影响分析(1)主梁应力、位移标准差影响分析
主梁应力、位移标准差与误差水平基本呈线性变化,在8%误差水平下,引起的各跨跨中位移标准差最大值为1.5 mm,混凝土主梁应力标准差最大值为0.07 MPa,钢主梁应力标准差最大值为1.64 MPa,与均值相比均很小,可忽略不计。
(2)主塔应力、位移标准差影响分析
主塔应力标准差随着塔身高度的增加标准差逐渐减少,位移标准差随着塔身高度的增加而逐渐增大,呈非线性分布,且误差水平越高,非线性越明显。在8%误差水平下,引起的主塔位移标准差最大值为2.2 mm,钢箱应力标准差最大值为4.1 MPa,与均值相比均很小,主塔总体应力水平较低,不控制设计。
(3)拉索应力标准差影响分析
在不同拉索初拉力误差水平下,拉索成桥应力均值、标准差见表 4。
| 索号 | 均值 | 2%标准差 | 5%标准差 | 8%标准差 |
| N1 | 529.7 | 10.3 | 25.8 | 41.3 |
| N2 | 529.1 | 10 | 25.1 | 40.2 |
| N3 | 528.1 | 9.7 | 24.2 | 38.8 |
| N4 | 555.2 | 9.9 | 24.8 | 39.6 |
| N5 | 531.5 | 9.2 | 23.1 | 37 |
| N6 | 497.9 | 8.6 | 21.6 | 34.5 |
| N7 | 580.6 | 10.4 | 25.9 | 41.5 |
| N8 | 569.5 | 10.5 | 26.2 | 42 |
| N9 | 553.5 | 10.2 | 25.6 | 40.9 |
| N10 | 527.6 | 10 | 24.9 | 39.8 |
| W1 | 527.2 | 10.4 | 25.9 | 41.5 |
| W2 | 526.1 | 10.1 | 25.1 | 40.2 |
| W3 | 526.9 | 9.7 | 24.2 | 38.7 |
| W4 | 554.9 | 9.9 | 24.9 | 39.8 |
| W5 | 532.9 | 9.3 | 23.3 | 37.2 |
| W6 | 498.7 | 8.6 | 21.5 | 34.4 |
| W7 | 583.8 | 10.4 | 26 | 41.7 |
| W8 | 573.7 | 10.5 | 26.2 | 41.9 |
| W9 | 553.9 | 10.2 | 25.5 | 40.8 |
| W10 | 527.9 | 9.9 | 24.8 | 39.6 |
由表 4可知,拉索应力标准差与误差水平基本呈线性变化,随误差水平的提高,拉索应力标准差逐渐增大。索力应力最大值为W7拉索,对应的拉应力值为583.8 MPa,在8%的误差水平下,对应的标准差为41.7 MPa。
2.5 索力误差水平对结构可靠度的影响分析不同的索力误差水平对应不同的结构可靠度,由以上分析可知,主塔总体应力水平低,不同拉索初拉力对应力和位移的影响不起控制作用。为研究拉索误差水平对结构可靠度的影响,选取拉索应力,进行可靠度影响分析,为确定拉索施工控制精度值提供必要的理论支撑。
根据《公路斜拉桥设计细则》(JTG/T D65-01—2007)第3.4.1条规定,运营状态斜拉索的安全系数不应小于2.5,即拉索的应力容许值为1 860/2.5=744 MPa。
由以上计算可知,索力误差水平为2%,5%和8%时拉索应力值小于744 MPa的可靠度水平均为100%;标准差较大,且随索力误差水平呈线性变化,对于拉索应力最大的拉索W7,根据统计学中“3σ”原则,标准差在(744-583)/3=53.7时为容许误差极限值,由线性关系可求得对应的拉索误差水平为10.3%,考虑目前施工安装技术水平,建议将索力安装误差控制在5%以内。
3 结论建立了考虑施工阶段的随机有限元分析模型,以拉索初拉力为随机变量,进行了结构构件响应的敏感性分析,并分析了结构响应随误差水平的变化情况,同时,对控制截面应力进行了可靠性分析,研究表明:
(1)因主塔、主梁、拉索及预应力的非对称布置,主塔、主梁的应力及变形和拉索的应力呈现出显著的非对称性,对应的敏感参数差异较大。
(2)因主梁受力为主,拉索受力为辅,N2,N4,N6,N7,W2,W3拉索应力只受自身初拉力影响,其他索力的影响可以忽略不计。成桥索力受拉索初拉力误差影响显著,且对自身的拉索初拉力误差最敏感,起控制作用。
(3)两边主梁及主塔跨应力、位移标准值受拉索误差水平影响较小,不控制设计。
(4)拉索安装误差水平由成桥索力控制,建议将索力安装误差控制在5%以内。
| [1] | 胡方健, 李国平. 自重和索力偏差对混凝土斜拉桥施工受力状态的影响[J]. 同济大学学报:自然科学版 , 2012, 42 (2) : 191-197 HU Fang-jian, LI Guo-ping. Influences of Deviation of Gravity and Cable Tension Force on Construction State of Cablestayed Concrete Bridges[J]. Journal of Tongji University:Natural Science Edition , 2012, 42 (2) : 191-197 |
| [2] | 苏成, 范学明. 考虑材料与荷载变异时崖门大桥施工阶段随机分析[J]. 桥梁建设 , 2003 (1) : 62-65 SU Cheng, FAN Xue-ming. Stochastic Analysis of Yamen Bridge at Erection Stage in Consideration of Variant Material and Loading Parameters[J]. Bridge Construction , 2003 (1) : 62-65 |
| [3] | 施志勇, 李欣然, 周雄伟, 等. 在施工过程中施工误差对大跨径斜拉桥极限承载力影响的研究[J]. 结构工程师 , 2008, 24 (3) : 145-151 SHI Zhi-yong, LI Xin-ran, ZHOU Xiong-wei, et al. Research on Ultimate Bearing Capacity for Long-span Cable-stayed Bridges due to Construction Deviation during Erection[J]. Structural Engineers , 2008, 24 (3) : 145-151 |
| [4] | 庞键.大跨度预应力混凝土斜拉桥收缩徐变效应随机分析与可靠度分析[D].广州:华南理工大学, 2010. PANG Jian. Stochastic Analysis and Reliability Analysis of Shrinkage and Creep Effects for Long-span Prestressed Concrete Cable-stayed Bridge[D].Guangzhou:South China University of Technology, 2010. http://cdmd.cnki.com.cn/article/cdmd-10561-2010228977.htm |
| [5] | 向绪霞, 金恩, 陈德伟. 斜拉索的施工随机误差对斜拉桥的影响[J]. 结构工程师 , 2011, 27 (1) : 154-160 XIANG Xu-xia, JIN En, CHEN De-wei. Response Analysis of Cable-Stayed Bridges Due to Random Deviation of Stay Cable Tension[J]. Structural Engineers , 2011, 27 (1) : 154-160 |
| [6] | 官华, 上官兴. 混凝土斜拉桥施工误差的静力随机分析[J]. 中外公路 , 2013, 33 (1) : 159-163 GUAN Hua, SHANGGUAN Xing. Static Random Analysis of Concrete Cable-stayed Bridges Due to Construction Error[J]. Journal of China & Foreign Highway , 2013, 33 (1) : 159-163 |
| [7] | 周雄伟.施工误差对大跨径斜拉桥在施工过程中极限承载力影响的研究[D].上海:同济大学, 2007. ZHOU Xiong-wei. Research on Ultimate Bearing Capacity for Long-span Cable-stayed Bridge due to Construction Error[D]. Shanghai:Tongji University, 2007. http://cdmd.cnki.com.cn/article/cdmd-10247-2007222896.htm |
| [8] | 刘世明, 刘永健, 琚明杰. 无背索曲塔曲梁斜拉桥施工优化[J]. 公路交通科技 , 2015, 32 (11) 68-74, 80 LIU Shi-ming, LIU Yong-jian, JU Ming-jie. Construction Optimization of Curved-pylon and Curved-girder Cable-stayed Bridge without Back Stay[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (11) 68-74, 80 |
| [9] | 刘世明, 赵顺波, 李晓克. 大跨人行异型斜拉桥静、动力及抗震性能分析[J]. 桥梁建设 , 2012, 42 (4) : 45-50 LIU Shi-ming, ZHAO Shun-bo, LI Xiao-ke. Analysis of Static, Dynamic and Seismic Performance of Long Span Irregular-Shape Pedestrian Cable-Stayed Bridge[J]. Bridge Construction , 2012, 42 (4) : 45-50 |
| [10] | 刘世明, 刘永健. 无背索曲塔曲梁斜拉桥参数敏感性分析[J]. 公路交通科技 , 2014, 31 (2) : 54-59 LIU Shi-ming, LIU Yong-jian. Analysis of Parameter Sensitivity for Curved-pylon and Curved-girder Cable-stayed Bridge without Back-stay[J]. Journal of Highway and Transportation Research and Development , 2014, 31 (2) : 54-59 |
| [11] | 琚明杰.无背索曲塔曲梁斜拉桥受力性能研究[D].西安:长安大学, 2011. JU Ming-jie. Mechanical Performance Analysis on Curved-pylon and Curved-girder Cable-stayed Bridge without Backstay[D]. Xi'an:Chang'an University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10710-1013019423.htm |
| [12] | 李晓克, 刘世明, 杨竹林. 预应力混凝土连续箱梁桥设计实例分析. 北京:中国电力出版社[M]. 2015 : 24 -27. LI Xiao-ke, LIU Shi-ming, YANG Zhu-lin. Design Instance Analysis of Prestressed Concrete Continuous Box-girder Bridge. Beijing:China Electric Power Press[M]. 2015 : 24 -27. |
| [13] | 陈兆栓.预应力混凝土斜拉桥施工监控概率方法研究[D].南京:华南理工大学, 2012. CHEN Zhao-shuan. Research on Probabilistic Method of Construction Monitoring and Control of Prestressed Concrete Cable-stayed Bridges[D]. Nanjing:South China University of Technology, 2012. http://cdmd.cnki.com.cn/article/cdmd-10561-1013151610.htm |
| [14] | 金路, 张壮南, 王春刚, 等. 基于蒙特卡罗的考虑随机初始缺陷的分析方法[J]. 工程力学 , 2012, 29 (S2) : 93-96 JIN Lu, ZHANG Zhuang-nan, WANG Chun-gang, et al. Monte Carlo-based Analysis Method Considering Random Intial Imperfections[J]. Engineering Mechanics , 2012, 29 (S2) : 93-96 |
 2016, Vol. 33
2016, Vol. 33
