扩展功能
文章信息
- 曲大义, 万孟飞, 王兹林, 许翔华, 王进展
- QU Da-yi, WAN Meng-fei, WANG Zi-lin, XU Xiang-hua, WANG Jin-zhan
- 基于交通波理论的干线绿波协调控制方法
- A Coordinate Control Method for Arterial Green Wave Traffic Based on Traffic-wave Theory
- 公路交通科技, 2016, 33(9): 112-119
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(9): 112-119
- 10.3969/j.issn.1002-0268.2016.09.018
-
文章历史
- 收稿日期: 2015-09-28
城市干线绿波协调控制协同考虑干线交叉口交通流运行的时空特性,系统考虑周期、相位相序、绿信比和相位差等控制参数,对干线交通运行进行控制,从而实现交通流在时间和空间上的分离,达到干线畅通有序的效果,这对于保证干线交通运行效率和缓解交通压力具有重要意义。国外学者Little[1]采用混合整数线性规划的方法,通过调整相位差寻求最大的绿波带宽度;随后Gartner等[2]针对不同路段交通流量和带宽需求提出了可变带宽的干线双向绿波控制模型;Hu等[3]在模糊控制理论的基础上,提出了一种通过调整时间参数和交通信号相位实现交通流控制的模糊系统;Tian等[4]基于系统分区技术,提出了通过调整子系统相位差实现子区绿波带宽最大和系统某方向带宽最大的信号配时方法;卢凯等[5-6]基于干线协调控制中的时距分析方法提出了进口单独放行方式下的双向绿波协调控制算法,进一步引入绿波带宽分配影响因子,构建了面向双向不同带宽需求的绿波控制优化模型;朱和等[7]从相位相序优化设计角度提出了基于NEMA的灵活相位相序协调控制方案;唐克双等[8]提出了非对称式绿波模型,以保证绿波带靠近上下游绿灯中间位置,提高绿波运行的稳定性;刘小明等[9]通过控制目标函数模型,建立了试探法与图形法相结合的绿波带宽计算方法;侯永芳[10]针对交通流量的影响,综合考虑不同方向车流对绿波带的需求以及控制模型的约束条件,建立了最大绿波带改进模型。
上述各类方法从获得更大绿波宽度角度研究了干线协调控制,其应用对干线协调控制有明显效果,在一定程度上缓解了交通拥挤,但从根本上忽略了干线绿波交通的内在机理。本文基于城市干线各交叉口之间的紧密关系和关联交叉口的排队特性,以线控系统绿波交通产生的内在机理为出发点,研究基于交通波理论的干线交叉口相位差优化模型,以实现干线多交叉口的优化控制。
1 问题描述城市干线绿波协调控制的基本思想是将干线所有信号交叉口作为一个控制系统,通过协调各交叉口绿灯起步时差,保证线控系统中的车辆从协调道路的第1个交叉口绿灯驶过后,一路绿灯通过后续多个路口;或进入下游路段后,能够跟随前方车队尾车不停车地驶至停车线,形成连续的交通流。这种协调控制方式能够满足干线大流量交通的通行需求,同时也能够减少车辆在交叉口的停车延误,提高交叉口通行能力。但实际的交通状况是,车流驶向下游交叉口时经常遇到红灯,或者因高峰期车流量较大,车辆到达下游队尾时,队尾车辆仍处于停车状态,迫使其停车排队,绿波协调控制实现的条件相对苛刻。基于此,要想实现干线交通的绿波控制,就要在合理的道路渠化与信号配时控制的基础上,从控制排队完全消散的角度设置相位差。
2 模型构建 2.1 干线系统描述本文中城市干线系统实现的是双向绿波交通。假定城市干线系统由n个交叉口组成,参与协调的是干线直行车流。相邻交叉口i与i+1停车线间的距离为L(i,i+1), 各车道设有排队检测器,距交叉口停车线的距离为Ls,可用于检测车流量与车速。由于车流具有随机性与离散性,若能够保证车辆连续、排队式的行驶,就达到了干线控制的理想效果,因此在线控系统中保证车流在交叉口间平稳行驶,一般作如下假设:
(1) 参与协调的直行车流稳定,左转与右转车流量不大,或外部输出与输入流量近似。
(2) 忽略黄灯时间,当前相位结束即为下一相位开始。
(3) 信号控制周期内干线系统的相序和相位数确定不变。
(4) 行人与非机动车跟随交通信号通行,忽略行人与非机动车辆的干扰。
2.2 干线绿波协调控制参数的优化干线控制系统的主要参数有周期时长、相位相序、绿信比和相位差。为实现绿波协调控制,线控系统内的所有交叉口要根据具体的进口道渠化方案确定相位相序,然后采用共同的周期时长,综合考虑单个交叉口的绿灯时间和协调方向的交通需求来确定绿信比,最后通过协调相邻交叉口的相位差实现干线主车流的绿波通行。
2.2.1 周期时长的确定干线控制中,通常先按照单点定时信号配时的方法计算各个交叉口的周期时长,再选出交通负荷最高的关键交叉口的周期时长为公用周期时长。单点信号配时一般利用韦伯斯特方法计算最佳信号周期[11],即:
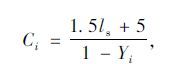
|
(1) |
式中,Ci为交叉口i的周期长度;ls为总损失时间,表示前后损失时间与全红时间之和;Yi为交叉口i的总流量比。
该方法以关键交通流延误时间最小为目标,求得交叉口的1个最佳信号周期。另外,考虑定时协调控制理想周期的确定方法,引入交叉口间距,计算周期时长为:
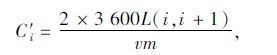
|
(2) |
式中,C′i为交叉口i的周期;L(i,i+1)为交叉口i与交叉口i+1的停车线间距;v为车辆在路段上的平均行驶速度;m为常数量,为非负整数。
综合两种周期时长确定方法,赋值不同的权重,得到干线公共周期时长为:
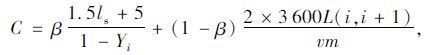
|
(3) |
式中β为权重值,取值在0~1之间。
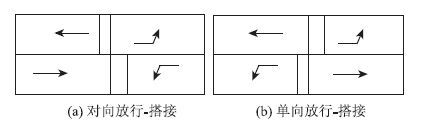
2.2.2 相位相序的确定设计相位相序时首先要保证通行能力。为提高大流量通行方向的通行能力,保证小流量通行方向的绿灯利用率,可采用相位搭接的处理方法。如图 1所示,相位搭接能够给予某通行方向更大的通行权,在周期时长不变的条件下,实现相序的合理组合,保证通行能力。
|
| 图 1 搭接放行 Fig. 1 Lap release |
| |
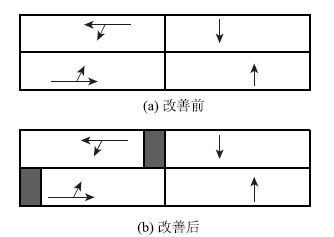
与相位搭接类似的“虚相位”的设置能够实现放行时间的错开,如图 2所示。对于直行左转对向混放的路口,直行车与对向左转车产生交织,降低了交叉口通行能力,增设“虚相位”能够将双向车辆放行时间适当错开,在绿灯开始或结束的几秒时间里,保证左转车通过交叉口时与直行车无冲突。
|
| 图 2 增加虚相位 Fig. 2 Adding virtual phase |
| |
2.2.3 绿信比的确定
通常依据交叉口各进口道各流向的设计交通量以及车道渠化方案,考虑周期损失时间以及配时条件、服务水平的要求,计算各流向的绿信比,但对于参与干线协调的交叉口还要考虑干线上、下游交叉口与首、末交叉口的需求与供给关系。
(1) 干线上、下游交叉口之间
干线系统中参与协调的直行车流在通过上游交叉口后仍多数保持直行通过下游交叉口时,要考虑上、下游交叉口的直行车道数,总体上应满足下述关系:
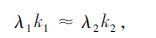
|
(4) |
式中,λ1为上游路口直行绿灯时间;k1为上游路口直行车道数;λ2为下游路口直行绿灯时间;k2为下游路口直行车道数。
式(4)保证上、下游交叉口之间的通行总供给大体一致。车流驶向下游时,若车道数由多变少,可通过增加下游绿信比满足上游通行能力;反之,车道数增多,可减小下游绿信比,这有效避免了交叉口间路段的拥堵。
(2) 干线协调方向的首、末交叉口
干线协调方向的首、末交叉口可以理解为总入口和总出口。为了保证干线协调效果,避免发生大规模拥堵情况,应按照少输入多输出的原则严格控制总入口与总出口的车流情况。协调方向的总入口一般通过减小绿信比的方式减少干线的整体需求,总出口可通过增加绿信比来保证干线足够的输出量,具体的增减数值一般在-10~+10 s之间。
2.3 基于交通波理论的相位差优化干线主车流在上游交叉口绿灯期间通过,不管下游交叉口在上一绿灯时间内排队完全消散还是存在滞留车辆,到达下游交叉口时只有满足下游交叉口的排队车辆完全消散才能实现绿波交通。若下游交叉口排队过长,上游交叉口车辆行驶到下游交叉口排队车辆队尾时,队尾车辆未能启动则会导致从上游交叉口行驶过来的车辆再次停车,由此产生连锁反应,导致路段车辆排队上溯至上游交叉口,造成上游交叉口溢出,故相位差的确定要考虑车辆的排队特性。
当交叉口信号状态为绿灯时,车辆以行驶状态通过交叉口。若信号状态为红灯,车辆要经过行驶、减速、停车、加速、再行驶5种行车状态,等待下一周期绿灯时通过交叉口,在此过程中不管是减速至停车还是加速至行驶速度,都存在信号状态从前车依次向后车传递的现象,即两种不同密度部分的分界面掠过一辆辆车向车队后部传播,产生车流波动的传递,表现为车辆排队的集结与消散。基于车流波动理论和连续性方程,确定波速方程为[12]:
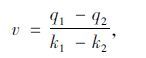
|
(5) |
式中,q1与q2为两种不同交通状态下的交通量;k1与k2为两种不同交通状态下的车流密度。
从运动学角度分析停车波与启动波的传播过程,确定停车波与启动波的波速方程分别为[13-14]:
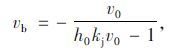
|
(6) |

|
(7) |
式中,vb为停车波波速;v0为排队前的行驶速度;h0为排队前相邻车辆的车头时距;kj为阻塞密度;vd为启动波波速;v1为启动后的行驶速度;h1为启动后相邻车辆的车头时距。
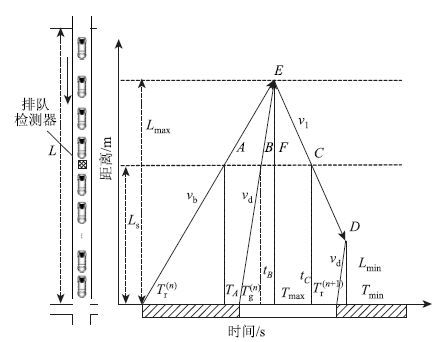
信号交叉口车辆排队时距图见图 3,横轴表示时间,纵轴表示距离。
|
| 图 3 信号交叉口车辆排队时距图 Fig. 3 Time-distance curve of vehicle queuing at signal control intersection |
| |
假设交叉口进口道在过去的n-1个信号周期里没有滞留车辆,则排队过程可分为以下几个阶段:
Tr(n)时刻,第n个信号周期的红灯启亮,驶向交叉口停车线的头车开始减速停车形成排队,后续车辆减速到排队队尾依次排队,形成速度为vb的停车波向上游传播,车辆陆续进入停车状态,停车波到达排队检测器的时刻为tA。
Tg(n)时刻,绿灯启亮,停车线处的头车开始加速启动,并将启动信号依次向队尾传播,形成速度为vd的启动波向上游传播,停止车辆变为运动状态逐步进入饱和状态,启动波到达排队检测器的时刻为tB。
当停车波与启动波到达同一位置,即启动波传播到排队队列尾部,此时排队完全消散[15],该位置为排队最远位置,记为Lmax,对应的时刻为Tmax。排队消散的车辆处于行驶状态,产生速度为v1的行驶波向下游交叉口传播,排队队列尾部车辆通过排队检测器的时间为tC。
设排队队尾车辆到达下游停车线位置时的时刻为Ts,第n个信号周期绿灯结束时刻为Tr(n+1),则Ts与Tr(n+1)之间存在两种关系:
状态1:Ts≤Tr(n+1),排队队尾车辆到达停车线处时信号灯为绿灯,排队车辆全部通过交叉口。
状态2:Ts>Tr(n+1),第n个信号周期绿灯结束时,排队队尾车辆未通过交叉口,未通过的车辆开始累计排队,自停车线位置形成速度为v′d的停车波向后蔓延,当车辆排队蔓延至行驶波位置时,车辆排队长度达到最小值,记为Lmin,对应的时刻为Tmin。
由上文分析可知,停车波和启动波相遇位置是排队最远位置,故最大排队长度为:
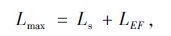
|
(8) |
式中,Lmax为下游交叉口最大排队长度;Ls为排队检测器到下游交叉口停车线的距离;LEF为排队检测器到排队最远位置的距离。
由几何关系得:
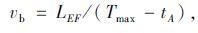
|
(9) |
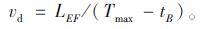
|
(10) |
根据三角形定则知:
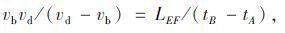
|
(11) |
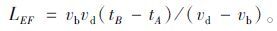
|
(12) |
将式(12)代入式(8)得到最大排队长度为:

|
(13) |
同时,最大排队队尾车辆到达停车线的时刻为:
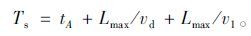
|
(14) |
当满足Tr(n+1)≥tA+Lmax/vd+Lmax/v1时,交通处于状态1,排队车辆在1个信号周期内能够全部消散,否则处于状态2,部分排队车辆累计排队,滞留排队长度为:
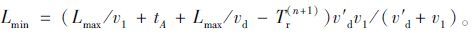
|
(15) |
为避免车辆排队溢出,在车流到达下游交叉口前需有足够一部分绿灯时间用于消散排队车辆,可从两种情况考虑。
一种是上游交叉口车流在绿灯启亮后到达排队队尾时恰好不排队,即车流到达队尾时下游交叉口启动波与停车波相遇,此时相位差满足:
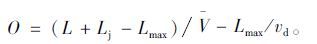
|
(16) |
另一种是上游交叉口车流到达下游停车线时,下游排队车辆队尾恰好通过停车线,此时满足:
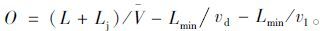
|
(17) |
故当下游交叉口相对上游交叉口的相位差满足以下条件时,干线上的主车流能够不停车通过:
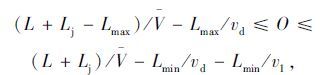
|
(18) |
式中,O为下游交叉口相对上游交叉口的相位差;L为路段长度;Lj为上游交叉口长度;V-为路段平均车速。
运用交通波理论对干线车辆排队特性进行解析,可知干线主车流到达各交叉口时排队完全消散是干线绿波交通控制优化的目标,基于此建立了交叉口相位差模型,相位差的合理区间为:
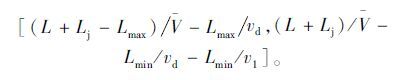
|
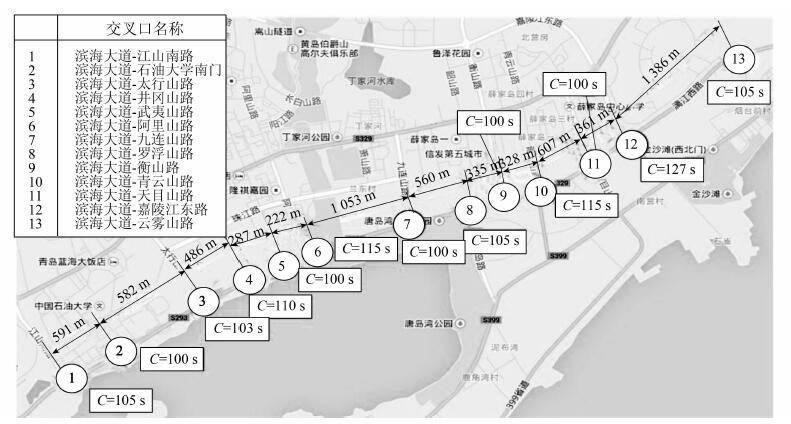
选取青岛市滨海大道沿线13个灯控路口为研究对象,调查得到各路口信号控制现状,如图 4所示。各路口采用单点控制,信号方案如表 1所示。由于信号控制方案的不合理和交叉口间缺乏协调,造成交通状况稳定的滨海大道间歇性停车现象严重,沿线的阿里山路路口、青云山路路口和嘉陵江东路路口各相位绿灯损失现象严重。
|
| 图 4 滨海大道各路口信号控制现状 Fig. 4 Signal control state of intersections on coastal road |
| |
3.2 方案设计
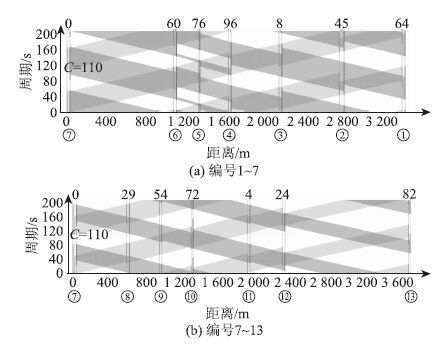
依据滨海大道路况稳定、各交叉口间距离适中、信号放行方式类似和信号周期相近的特点,判定各交叉口关联性较强,具备双向绿波协调控制的条件。根据滨海大道交通量的调查数据,按照上文中的计算方法,将周期统一为110 s,各交叉口的相位相序方案、绿灯时间如表 2所示。由式(16)、(17)计算得到相邻交叉口间的相位差区间。以保证双向绿波带宽最大为目标,在合理区间内确定相位差的具体值,如表 3所示。双向绿波协调控制方案的效果如图 5所示。
| 编号 | 交叉路段 | 距离/m | 信号周期/s | 设计速度/(km·h-1) | 绝对相位差/s | ||
| 优化前 | 优化后 | 正向 | 反向 | ||||
| 1 | 江山南路 | 0 | 105 | 110 | 60 | — | 64 |
| 2 | 石油大学南门 | 591 | 100 | 110 | 60 | 60 | 45 |
| 3 | 太行山路 | 582 | 103 | 110 | 60 | 60 | 8 |
| 4 | 井冈山路 | 486 | 110 | 110 | 50 | 60 | 96 |
| 5 | 武夷山路 | 287 | 100 | 110 | 50 | 50 | 76 |
| 6 | 阿里山路 | 222 | 115 | 110 | 60 | 50 | 60 |
| 7 | 九连山路 | 1 053 | 100 | 110 | 60 | 60 | 0 |
| 8 | 罗浮山路 | 560 | 105 | 110 | 55 | 60 | 29 |
| 9 | 衡山路 | 335 | 100 | 110 | 55 | 55 | 54 |
| 10 | 青云山路 | 328 | 115 | 110 | 55 | 55 | 72 |
| 11 | 天目山路 | 607 | 100 | 110 | 55 | 55 | 4 |
| 12 | 嘉陵江东路 | 361 | 127 | 110 | 65 | 55 | 24 |
| 13 | 云雾山路 | 1 386 | 105 | 110 | — | 65 | 82 |
|
| 图 5 滨海大道双向绿波协调时距图 Fig. 5 Time-distance chart of bidirectional green wave coordination for coastal road |
| |
3.3 优化效果
双向绿波协调控制方案使滨海大道通行效率得到明显改善,主要体现在车辆出行时间和停车次数两项指标上。采用浮动车法对滨海大道调优前后的旅行时间和停车次数指标进行跟踪调查,对比结果见表 4。优化前后对比表明,实施双向绿波协调控制方案后滨海大道自东向西方向的总旅行时间从779 s变为564 s,减少27.5%,总停车次数从6次变为2次;自西向东方向的总旅行时间从806 s变为592 s,减少26.5%,总停车次数从5次变为2次。
| 干线方向 | 交叉路段 | 调优前 | 调优后 | ||
| 旅行时间/s | 停车次数/次 | 旅行时间/s | 停车次数/次 | ||
| 滨海大道自东向西 | 云雾山路 | 0 | 0 | 0 | 0 |
| 嘉陵江东路 | 90 | 0 | 88 | 0 | |
| 天目山路 | 145 | 1 | 116 | 0 | |
| 青云山路 | 200 | 0 | 153 | 0 | |
| 衡山路 | 245 | 1 | 174 | 0 | |
| 罗浮山路 | 267 | 0 | 196 | 0 | |
| 九连山路 | 323 | 1 | 230 | 0 | |
| 阿里山路 | 443 | 1 | 333 | 1 | |
| 武夷山路 | 470 | 0 | 352 | 0 | |
| 井冈山路 | 510 | 1 | 372 | 0 | |
| 太行山路 | 598 | 0 | 410 | 0 | |
| 石油大学南门 | 680 | 1 | 510 | 1 | |
| 江山南路 | 779 | 0 | 564 | 0 | |
| 滨海大道自西向东 | 江山南路 | 0 | 0 | 0 | 0 |
| 石油大学南门 | 54 | 1 | 38 | 0 | |
| 太行山路 | 132 | 0 | 96 | 0 | |
| 井冈山路 | 188 | 0 | 153 | 1 | |
| 武夷山路 | 213 | 1 | 178 | 0 | |
| 阿里山路 | 261 | 0 | 205 | 0 | |
| 九连山路 | 335 | 1 | 275 | 0 | |
| 罗浮山路 | 398 | 0 | 315 | 0 | |
| 衡山路 | 456 | 0 | 347 | 0 | |
| 青云山路 | 559 | 1 | 420 | 1 | |
| 天目山路 | 678 | 0 | 470 | 0 | |
| 嘉陵江东路 | 710 | 0 | 499 | 0 | |
| 云雾山路 | 806 | 1 | 592 | 0 | |
4 结论
鉴于城市干线各交叉口间的关联性,本文从周期、相位相序、绿信比、相位差4种控制参数入手,对干线绿波交通进行了优化研究。采用最佳周期与定时控制理想周期的加权值作为公共周期,提出了搭接、“虚相位”等新的交通放行方式。考虑上、下游交叉口与首、末交叉口的需求与供给关系,确定了交叉口绿信比。基于交通波理论,阐述了相邻交叉口的排队特性,进一步说明了干线绿波交通的内在机理是要保证下游排队车辆完全消散,基于此建立了干线交叉口相位差优化模型。选取青岛市滨海大道的干线控制优化进行案例分析,验证了4种控制参数对于干线绿波协调控制的可行性和所建相位差模型的实用性。从干线整体车辆的停车次数和旅行时间角度来看,评价指标提升率均在25%以上,即实施干线绿波协调控制后车辆停车次数明显减少,旅行时间明显变短。
| [1] | LITTLE J D C. The Synchronization of Traffic Signals by Mixed-integer Linear Programming[J]. Operations Research , 1966, 14 (4) : 568-594 |
| [2] | GARTNER N H, ASSMANN S F, LASAGA F, et al. Multiband: A Variable Bandwidth Arterial Progression Scheme[J]. Transportation Research Record , 1990, 1287 : 212-222 |
| [3] | HU Y, THOMAS P, STONIER R J. Traffic Signal Control Using Fuzzy Logic and Evolutionary Algorithms [C]//2007 IEEE Congress on Evolutionary Computation. Singapore:IEEE 2007: 1785-1792. |
| [4] | TIAN Z, URBANIK T. System Partition Technique to Improve Signal Coordination and Traffic Progression[J]. Journal of Transportation Engineering , 2007, 133 (2) : 119-128 |
| [5] | 卢凯, 徐建闽, 李轶舜. 进口单独放行方式下的干道双向绿波协调控制数解算法[J]. 中国公路学报 , 2010, 23 (3) : 96-99 LU Kai, XU Jian-min, LI Yi-shun. Algebraic Method of Arterial Road Coordinate Control for Bidirectional Green Wave under Signal Design Mode of One-phase-one-approach[J]. China Journal of Highway and Transport , 2010, 23 (3) : 96-99 |
| [6] | 卢凯, 郑淑鉴, 徐建闽, 等. 面向双向不同带宽需求的绿波协调控制优化模型[J]. 交通运输工程学报 , 2011, 11 (5) : 102-107 LU Kai, ZHENG Shun-jian, XU Jian-min, et al. Green Wave Coordinated Control Optimization Models Oriented to Different Bidirectional Bandwidth Demands[J]. Journal of Traffic and Transportation Engineering , 2011, 11 (5) : 102-107 |
| [7] | 朱和, 常玉林. 基于灵活相位的双向绿波协调控制[J]. 公路交通科技 , 2013, 30 (7) : 141-143 ZHU He, CHANG Yu-lin. Bidirectional Green Wave Coordinative Control Based on Flexible Phase[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (7) : 141-143 |
| [8] | 唐克双, 孔涛, 王奋, 等. 一种改进的多带宽干线协调控制模型[J]. 同济大学学报:自然科学版 , 2013, 41 (7) : 1002-1005 TANG Ke-shuang, KONG Tao, WANG Fen, et al. A Modified Multiband Model for Urban Arterial Coordinate Control[J]. Journal of Tongji University: Natural Science Edition , 2013, 41 (7) : 1002-1005 |
| [9] | 刘小明, 王力. 基于综合绿波带最宽的交叉口信号协调控制优化方法[J]. 吉林大学学报: 工学版 , 2013, 43 (1) : 62-67 LIU Xiao-ming, WANG Li. Optimization Method of Intersection Signal Coordinated Control Based on Integrated Green Wave Bandwidth Maximization[J]. Journal of Jilin University: Engineering and Technology Edition , 2013, 43 (1) : 62-67 |
| [10] | 侯永芳. 干线绿波交通信号控制方法研究 [D]. 长春: 吉林大学, 2015. HOU Yong-fang. Study on Green Wave Traffic Signal Control Method for Arterial Roads [D]. Changchun: Jilin University, 2015. http://cdmd.cnki.com.cn/article/cdmd-10183-1015594232.htm |
| [11] | 王炜, 过秀成. 交通工程学[M]. 南京: 东南大学出版社, 2011 . WANG Wei, GUO Xiu-cheng. Traffic Engineering[M]. Nanjing: Southeast University Press, 2011 . |
| [12] | 任福田, 刘小明. 交通工程学[M]. 北京: 人民交通出版社, 2012 . REN Fu-tian, LIU Xiao-ming. Traffic Engineering[M]. Beijing: China Communications Press, 2012 . |
| [13] | 姚荣涵, 曲大义, 王殿海. 基于运动学方程的停车波模型[J]. 吉林大学学报:工学版 , 2007, 37 (5) : 1050-1051 YAO Rong-han, QU Da-yi, WANG Dian-hai. Stop-wave Model based on Kinematic Equation[J]. Journal of Jilin University: Engineering and Technology Edition , 2007, 37 (5) : 1050-1051 |
| [14] | 曲昭伟, 王殿海, 姚荣涵. 信号交叉口起动波的运动学模型[J]. 吉林大学学报:工学版 , 2008, 38 (2) : 269-270 QU Zhao-wei, WANG Dian-hai, YAO Rong-han. Kinematic Model of Start Wave at Signalized Intersection[J]. Journal of Jilin University: Engineering and Technology Edition , 2008, 38 (2) : 269-270 |
| [15] | 贾婧. 车辆排队的链式反应模型及其数值模拟 [D]. 大连: 大连理工大学, 2012. JIA Jing. Chain Reaction Models and Numerical Simulation of Vehicle Queuing [D]. Dalian: Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/article/cdmd-10141-1012395213.htm |
 2016, Vol. 33
2016, Vol. 33


