扩展功能
文章信息
- 邓忠, 赵尚传, 刘斌云
- DENG Zhong, ZHAO Shang-chuan, LIU Bin-yun
- 基于多阶段定期检查数据的混凝土桥梁碳化耐久性评估方法
- An Evaluation Method for Carbonation Durability of Concrete Bridge Based on Multiple Periodic Inspection Data
- 公路交通科技, 2016, 33(9): 64-68
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(9): 64-68
- 10.3969/j.issn.1002-0268.2016.09.011
-
文章历史
- 收稿日期: 2014-04-26
2. 交通运输部公路科学研究所, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
截止2014年底,我国公路桥梁已达75.71万座,4 257.89万座[1],90%以上采用钢筋混凝土和预应力混凝土建造,由于环境侵蚀而导致的结构耐久性不足问题较为突出。统计资料显示[2],我国桥梁平均寿命仅约30 a左右;而美国钢筋混凝土桥的期望寿命基本在70~80 a,预应力混凝土桥的期望寿命在65~100 a;日本山区的普通钢筋混凝土桥面板使用寿命为60 a;荷兰的混凝土桥梁使用寿命分布主要为80~100 a。
一般大气环境是我国混凝土桥梁常见的暴露环境[3],由于混凝土碳化而导致的钢筋锈蚀是混凝土桥梁最常见的一种耐久性失效现象,在导致公路桥梁耐久性病害的因素中占32%,如在川黔线上部分混凝土桥梁的碳化深度达到钢筋表面比率的40%,钢筋锈蚀严重[4]。为保障桥梁结构的使用年限,我国公路交通行业加强了对桥梁的养护管理工作。其中,检测评估是桥梁养护链的一个关键环节,评估结果的合理性,决定了养护决策的科学性。
国内外对于混凝土碳化机理研究已较为成熟,建立了许多材料层次的碳化模型,如Papadakis模型[5]、张誉模型[6]等,利用这些模型可以对构件中的检测点进行碳化耐久寿命评估。然而,在实际评估过程中,发现材料层次的模型并不能很好地适应于混凝土构件的碳化寿命评估,如:桥梁混凝土构件暴露面太多,其耐久性应当是暴露面的综合体现,而非单个测点的评估,如果测点之间出现评估结果差别较大的情况,则难以做出合理判断;再如,模型中一些参数(混凝土强度、保护层厚度等),在实际检测时,其结果存在不确定性,如何考虑这种不确定性的影响,现有模型没有给出。
由于耐久性与使用年限相关,其评估过程最好与成时间序列的耐久性数据相结合。现有评估方法,均没有考虑到这点,如模糊随机概率理论[7-8]、采用灰色系统理论来预测既有钢筋混凝土结构的剩余使用寿命[9]、基于人工神经网络对混凝土碳化深度进行预测[10]、基于可靠度理论对碳化寿命进行评估[11-13]。文献[14]采用可靠度理论,基于小样本数据对桥梁结构做出碳化寿命评估,简洁明了,但是对于构件测点的选择非常苛刻,测点要求能够反映整体构件的耐久性特征,如果测点选择不合理,得到的耐久性评价结果可能与桥梁结构实际情况存在较大偏差。
当前,公路桥涵养护规范[15]规定了定期检查的要求,周期不得超过3 a,特大桥不得超过1 a。定期检查中包含了混凝土保护层、混凝土强度、混凝土碳化深度、钢筋锈蚀情况等与结构耐久性相关的指标数据。这些呈时间序列的检查数据为桥梁耐久性评估提供了有效支撑。而目前这种利用多次时间序列数据的评估方法研究不多,限制了多阶段检查数据在耐久性评估中的应用。本文利用先验条件概率理论,通过对不同检测时间段的构件碳化失效概率分析,建立了利用多阶段定期检查数据的桥梁混凝土碳化耐久性评估方法,考虑碳化过程的随机性、多阶段检查数据的利用以及现场出现数据异常值的处理方法,通过算例验证了该方法的可操作性,为公路桥梁混凝土构件碳化耐久性评估提供了参考和依据。
1 利用多阶段检查数据的碳化失效评估方法 1.1 碳化评估理论在多阶段定期检查过程中,将j阶段之前的检查结果作为先验条件,利用先验条件概率理论,建立利用多阶段定期检查数据的混凝土桥梁碳化耐久性评估方法。设桥梁运行tj年时检测的总体碳化深度记为xj,总体保护层厚度记为cj。若结构在已运行tj年时检查钢筋未发生锈蚀,可表示为混凝土总体保护层厚度大于实测碳化深度cj>xj(先验条件),则结构的剩余碳化寿命t-tj大于继续服役期望值Y的可靠性可表示为条件概率的形式:
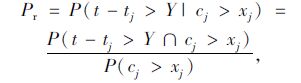
|
(1) |
其中
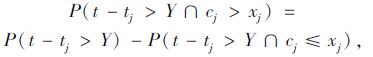
|
(2) |
而事件t-tj>Y的含义是结构未发生碳化失效,事件cj≤xj的含义是结构已发生碳化失效,故P(t-tj>Y∩cj≤xj)=0,由此式(1)可化简为:
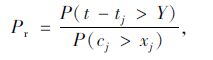
|
(3) |
相应的碳化失效概率为:
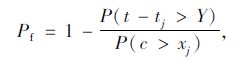
|
(4) |
式中,t为耐久年限,可表示为t=(cj/kj)2;kj为前j阶段检查时的碳化系数,为随机变量;cj为第j阶段检查时的钢筋混凝土总体保护层厚度,由现场检查得到,为随机变量;xj为tj年检查得到的总体碳化深度,为随机变量;Y为继续服役期望值。
以钢筋开始锈蚀作为耐久性极限状态,则混凝土结构碳化功能函数为:
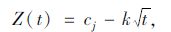
|
(5) |
对于式(4)中的P(t-tj>Y)和P(cj>xj)均表示功能函数Z=cj-kt的可靠概率,其中Y,tj为确定性变量,cj,xj,kj均为随机变量,将随机变量当量正态化后利用设计验算点法[4, 16]即可求得g1=Y+tj-(cj/kj)2和g2=xj-cj的可靠度指标β1,β2,故P(t-tj>Y)=Φ(-β1),P(cj>xj)=Φ(-β2)。
从而式(4)可写为:
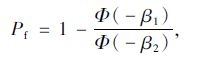
|
(6) |
相应的碳化可靠性指标:
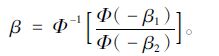
|
(7) |
式中,Φ为标准正态分布的概率函数。
混凝土结构耐久性设计规范[3]中指出欧洲一些工程用可靠度方法进行环境作用下的混凝土结构耐久性设计时,与正常使用极限状态相应的可靠度指标取1.8,失效概率不大于5%。因此本文以失效概率达到5%作为碳化耐久性极限状态。
1.2 首阶段检查参数取值对于单个测点的碳化深度记为xjn,表示j阶段检查的第n个测点的碳化深度,保护层厚度记为cjn。设首阶段检查(j=1)的混凝土保护层厚度数据为c11,c12,…,c1n,碳化深度为x11,x12,…,x1n,则它们的均值和标准差为:
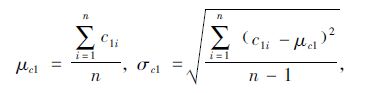
|
(8) |
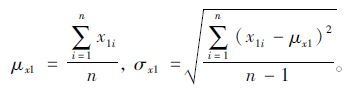
|
(9) |
碳化系数由kjn=xjn/tj求得,再通过数据统计分析确定参数分布,此法的前提是需要大量的数据作为支撑,多阶段检查数据刚好能满足这点。首次检测碳化系数的均值和标准差为:
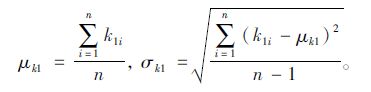
|
(10) |
求出以上参数后,采用设计验算点法得到可靠度指标β1,β2,代入式(6)得到碳化失效概率。
1.3 第j阶段检查参数取值多阶段定期检查数据的利用方法主要体现在随机参数的不断更新上。在已有前期检查数据的条件下,求出前j次检查所有保护层厚度、碳化系数的均值和标准差,作为总体分布参数,每进行新一阶段的检查,就对随机变量的统计参数进行更新,不断修正统计特征,降低耐久性指标的不确定性。
(1) 保护层厚度
假设第一次检查得到的n个保护层厚度数据为c11,c12,…,c1n;第二次得到的m个数据为c21,c22,…,c2m;第j次得到的v个数据为cj1,cj2,…,cjv。总体分布参数为:
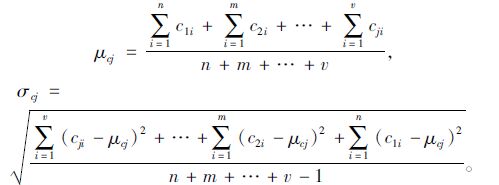
|
(11) |
(2) 碳化系数
碳化系数的总体分布参数处理方法同保护层厚度:
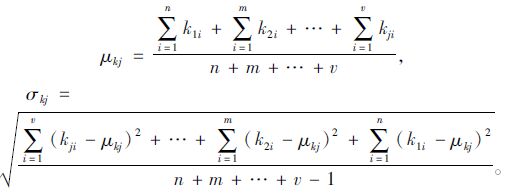
|
(12) |
(3) 碳化深度
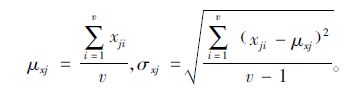
|
(13) |
多阶段检查的大量数据能够反映构件的整体情况,对每阶段的桥梁耐久性指标进行动态更新,以达到对混凝土结构碳化耐久性极限年限的逐步修订,掌握桥梁整体实时碳化情况。
1.4 异常情况判别鉴于施工质量优劣不同,钢筋保护层厚度存在偏差,实际检查中选择测点时难以避免此类区域,对于保护层厚度偏小区域的测点定义为异常情况。设第j次检查第k个测点的保护层厚度为cjk,总体保护层厚度服从正态分布cj~N(μ,σ2),若满足cjk<μ-2σ,按照小概率事件处理,认为此处的保护层厚度偏小是由施工质量导致的,不能代表结构总体的保护层厚度特征值,继续检查其他具有代表性区域。
2 算例 2.1 基于首次检查数据的耐久性评估某预制T梁桥已服役7 a,混凝土强度等级C50,对检测得到的混凝土保护层厚度、碳化深度(单位:mm)和碳化系数进行统计分析,经K-S检验均不拒绝服从正态分布,总体保护层厚度c1~N(40.48,14.96),碳化深度x1~N(5.24,2.72),碳化系数k1~N(1.95,1.1)。
将首次检查的混凝土总体保护层厚度大于实测碳化深度c1>x1作为先验条件,由式(6)算得T梁在继续服役年限内的碳化失效概率,结果见表 1。另外,将结构功能函数式(5)改写成Z(t)=cj-k·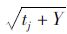
| 继续服役 期Y/a |
Φ(-β1)/% | Φ(-β2)/% | Pf/% | |
| 式(6) | 式(5) | |||
| 10 | 98.10 | 98.98 | 0.89 | 1.90 |
| 20 | 97.10 | 98.98 | 1.90 | 2.90 |
| 40 | 94.72 | 98.98 | 4.30 | 5.28 |
| 45 | 94.06 | 98.98 | 4.97 | 5.94 |
| 60 | 91.99 | 98.98 | 7.06 | 8.01 |
| 80 | 89.04 | 98.98 | 10.04 | 10.96 |
| 93 | 87.07 | 98.98 | 12.03 | 12.93 |
按照耐久性设计规范[3]取碳化失效概率Pf=5%(β=1.64),则在继续使用45 a后达到碳化耐久性极限状态,若不考虑先验条件,则在继续服役不到40 a达到了碳化耐久性极限状态。另一个我们关注的问题是在特大桥梁达到设计年限100 a时的碳化失效概率,即在Y=93 a时Pf=12.03%,远远大于5%的目标要求,即按当前耐久性设计规范,可认为该T梁不能满足100 a的碳化耐久性要求。对比式(5)、式(6)的结果,在服役同一时间考虑先验条件的碳化失效概率要小于采用功能函数直接计算的碳化失效概率,两种方法的结果差值与Φ(-β2)的大小有关,即先验条件的发生概率。需指出的是Φ(-β2)=P(c1>x1), 表示第一次检查时混凝土保护层厚度大于碳化深度的概率,是个定值。
2.2 基于首次和第二阶段检查数据的耐久性评估第二阶段检查后,得到了新的一批耐久性数据,为了克服首次耐久性评估存在的局限性,需对分布参数进行更新,将第一阶段和第二阶段的检查数据按照式(11)~(13)求出新的分布参数再进行新一轮的评估。
为了说明在多阶段中的应用,在tj=10 a时进行第二阶段检查(j=2),假设总体保护层厚度c2~N(39.4,14.3),碳化深度x2~N(6.1,3.0),碳化系数k2~N(1.85,0.9), 计算得到的结果见表 2。
| 继续服役期 Y/a |
Φ(-β1) / % |
Φ(-β2) / % |
Pf/% | |
| 式(6) | 式(5) | |||
| 10 | 98.19 | 98.87 | 0.69 | 1.81 |
| 30 | 96.40 | 98.87 | 2.50 | 3.60 |
| 43 | 95.04 | 98.87 | 3.87 | 4.96 |
| 53 | 93.90 | 98.87 | 5.03 | 6.10 |
| 70 | 91.81 | 98.87 | 7.14 | 8.19 |
| 90 | 89.19 | 98.87 | 9.79 | 10.81 |
由表 2可见,在继续服役53 a和43 a时,式(6)和式(5)分别达到碳化耐久性极限状态,两种方法结果相差10 a。第二阶段评估时T梁仍不能满足100 a的碳化耐久性设计要求,但相比于表 1,耐久年限有较大的提高。从第一阶段评估的52 a到第二阶段评估的63 a,可见随机参数的变化对评估结果的影响很大,而测点的选取直接关系到随机参数的大小,基于多阶段检查数据的碳化耐久性评估方法能够避免测点选取上的局限性。综上,在碳化耐久性的评估中,应考虑多阶段检查数据和条件概率理论的应用,可达到逐步对混凝土结构碳化耐久性极限年限的修订。之后的多阶段评估过程同第二阶段,不再赘述。
3 结论采用条件概率理论建立了在役公路混凝土桥梁碳化耐久性寿命预测方法,本方法充分结合了公路桥梁养护规范[15]中有关桥梁定期检查的行业特点,考虑了多个时段检查数据所表达的耐久性信息,可根据不同时间检查数据对耐久性评估结果进行动态更新、调整。伴随着桥梁定期检查的多次进行,预测结果将越来越符合结构实际状况,可更加科学合理地支撑桥梁养护决策。
| [1] | 冯正霖. 我国桥梁技术发展战略的思考[J]. 中国公路 , 2015 (11) : 38-41 FENG Zheng-lin. Considerations on Development Strategy of Chinese Bridge Technology[J]. China Highway , 2015 (11) : 38-41 |
| [2] | 马建, 孙守增, 杨琦, 等. 中国桥梁工程学术研究综述[J]. 中国公路学报 , 2014, 27 (5) : 1-96 MA Jian, SUN Shou-zeng, YANG Qi, et al. Review on China's Bridge Engineering Research[J]. China Journal of Highway and Transport , 2014, 27 (5) : 1-96 |
| [3] | GB/T50476—2008,混凝土结构耐久性设计规范[S]. GB/T50476—2008, Code for Durability Design of Concrete Structures [S]. |
| [4] | 赵国藩, 金伟良, 贡金鑫. 结构可靠度理论[M]. 北京: 中国建筑工业出版社, 2000 . ZHAO Guo-fan, JIN Wei-liang, GONG Jin-xin. Theory of Structural Reliability[M]. Beijing: China Architecture & Building Press, 2000 . |
| [5] | PAPADAKIS V G. Effect of Supplementary Cementing Materials on Concrete Resistance Against Carbonation and Chloride Ingress[J]. Cement and Concrete Research , 2000, 30 (2) : 291-299 |
| [6] | 张誉, 蒋利学. 基于碳化机理的混凝土碳化深度实用数学模型[J]. 工业建筑 , 1998, 28 (1) : 16-19 ZHANG Yu, JIANG Li-xue. A Practical Mathematical Model of Concrete Carbonation Depth Based on the Mechanism[J]. Industrial Construction , 1998, 28 (1) : 16-19 |
| [7] | 杨则英, 黄承逵, 曲建波. 基于自适应神经-模糊推理系统和遗传算法的桥梁耐久性评估[J]. 土木工程学报 , 2006, 39 (2) : 16-20 YANG Ze-ying, HUANG Cheng-kui, QU Jian-bo. Durability Evaluation of Bridges Based on ANFIS and Genetic Algorithms[J]. China Civil Engineering Journal , 2006, 39 (2) : 16-20 |
| [8] | KIM Y M, KIM C K, HONG S G. Fuzzy Based State Assessment for Reinforced Concrete Building Structures[J]. Engineering Structures , 2006, 28 (9) : 1286-1297 |
| [9] | 仲伟秋.既有钢筋混凝土结构的耐久性评估方法研究[D].大连:大连理工大学,2003. ZHONG Wei-qiu. Study on Durability Evaluation Methods for Existing RCStructures[D].Dalian: Dalian University of Technology,2003. http://cdmd.cnki.com.cn/article/cdmd-10141-2004093879.htm |
| [10] | 陆春华, 刘荣桂. 应力状态下混凝土碳化深度的神经网络预测[J]. 哈尔滨工业大学学报 , 2008, 40 (10) : 1649-1652 LU Chun-hua, LIU Rong-gui. Carbonation Depth Prediction of Pre-stressed Concrete Based on Artificial Neural Network[J]. Journal of Harbin Institute of Technology , 2008, 40 (10) : 1649-1652 |
| [11] | HAN S H, PARK W S, YANG E I. Evaluation of Concrete Durability due to Carbonation in Harbor Concrete Structures[J]. Construction and Building Materials , 2013, 48 (11) : 1045-1049 |
| [12] | MARQUES P F, CHASTRE C, NUNES A. Carbonation Service Life Modeling of RC Structures for Concrete with Portland and Blended Cements[J]. Cement & Concrete Composites , 2013, 37 (37) : 171-184 |
| [13] | 刘均利, 方志. 考虑CO2排放的公路桥梁结构时变可靠度[J]. 公路交通科技 , 2013, 30 (1) : 74-79 LIU Jun-li, FANG Zhi. Time-dependent Reliability of Highway Bridge Considering CO2 Emission[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (1) : 74-79 |
| [14] | 任锋, 刘俊岩, 裴现勇, 等. 基于混凝土碳化的桥梁耐久可靠度分析[J]. 公路交通科技 , 2004, 21 (10) : 71-72 REN Feng, LIU Jun-yan, PEI Xian-yong, et al. Reliability Analysis of Bridge Durability Based on Concrete Carbonization[J]. Journal of Highway and Transportation Research and Development , 2004, 21 (10) : 71-72 |
| [15] | JTG H11—2004,公路桥涵养护规范[S]. JTG H11—2004,Code for Maintenance of Highway Bridges and Culvers[S]. |
| [16] | 张明. 结构可靠度分析——方法与程序[M]. 北京: 科学出版社, 2009 . ZHANG Ming. Structural Reliability Analysis: Methods and Procedures[M]. Beijing: Science Press, 2009 . |
 2016, Vol. 33
2016, Vol. 33
