扩展功能
文章信息
- 赵明华, 肖尧, 徐卓君, 杨超炜
- ZHAO Ming-hua, XIAO Yao, XU Zhuo-jun, YANG Chao-wei
- 基于莫尔破坏判据的溶洞顶板冲切破坏研究
- Study on Punching Shear Failure of Cave Roof in Karst Area Based on Mohr Failure Criterion
- 公路交通科技, 2016, 33(9): 58-63
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(9): 58-63
- 10.3969/j.issn.1002-0268.2016.09.010
-
文章历史
- 收稿日期: 2015-10-21
我国岩溶地质分布范围十分广泛,由于勘察较为粗糙,在实际工程中容易出现桥梁桩基选址错误的情况;然而由于变更桥址代价太大,所以桩基无可避免会作用在岩溶地基上[1]。岩溶区桩基设计的关键是保证溶洞顶板的稳定性,因此溶洞顶板成为了研究的主要对象。目前,许多学者在这方面做了相关的研究。黎斌等[2]基于三维有限单元法,对桩基础下的溶洞顶板进行了应力分析计算,并采用多元线性回归的方法求得桩底到溶洞顶部距离临界值与溶洞大小和单桩设计荷载之间的关系式;赵明华等[3-5]分别从抗冲切、抗剪切、抗弯拉3个方面对顶板厚度进行验算,并分析了节理裂隙对顶板承载能力的影响;曹文贵等[6]用数值流行方法确定了溶洞顶板最小安全厚度;赵明华等[7]引进突变理论,建立了岩溶区桥梁桩基承载力及其下伏溶洞顶板安全厚度的尖点突变模型;张慧乐等[8-9]基于室内模型试验,对岩溶区嵌岩桩的承载能力和破坏模式进行了研究,根据其试验结果可知:当溶洞顶板较薄,溶洞跨径较大时,容易发生冲切破坏。因此本文侧重研究溶洞顶板冲切破坏。
混凝土板冲切破坏理论研究已经比较成熟。Jiang和Shen[10]基于Mohr-coulomb准则和功能原理导出了混凝土板抗冲切极限荷载,并利用变分原理求得了冲切破坏体曲线方程;Yankelevsky和Leibowitz[11]建立了混凝土板冲切破坏的新模型,并导出了板受荷时承载力与位移的数学表达式。在此基础上,赵明华等[12]引入格里菲斯岩石强度破坏理论推导出了溶洞顶板冲切破坏极限承载力;雷勇等[13]基于Hoek-Brown岩石强度准则剪应力形式推导出了溶洞顶板最小安全厚度,并给出了各参数对承载力的影响分析。
溶洞顶板在冲切破坏过程中,应力状态极为复杂,而且岩石材料在受力时具有一定的非线性,现有的技术成果并不能解决工程中遇到的所有问题。因此,本文在现有研究基础之上,参考混凝土板冲切破坏相关理论成果,并引入莫尔二次抛物线型岩石破坏判据,通过变分原理推导冲切破坏曲线方程,并基于功能原理推导溶洞顶板抗冲切极限承载力,以此求得溶洞顶板最小安全厚度。本文的研究成果能弥补现有理论研究在某些工程条件下的不足,具有较强的实践意义。
1 莫尔二次抛物线型岩石破坏判据莫尔(Mohr,1900)统一考虑了三向应力状态下的库仑-纳维尔判据后认为:材料在极限状态下,剪切面上的剪应力就达到了随法向应力和材料性质而定的极限值。一般认为,该理论比较全面地反映了岩石的强度特征,它既适用于塑性岩石也适用于脆性岩石的剪切破坏[14]。岩性较硬至较软弱的岩石强度包络线近似于二次抛物线,如图 1所示。

|
| 图 1 二次抛物线型莫尔强度包络线 Fig. 1 Quadratic parabolic Mohr strength envelope |
| |
图 1中,σ1、σ3分别为大小主应力;σc、σt分别为岩石的抗压、抗拉强度;εn、γnt分别为拉伸、剪切应变率。
其表达式为:

|
(1) |
式中n为待定系数。
利用图 1中的关系,有:

|
(2) |
其中τ,tan2β和sin2β,从式(1)及图 1可知:
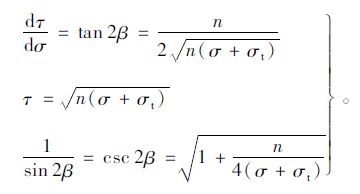
|
(3) |
将式(3)的有关项代入式(2),并消去式中的σ2,得到二次抛物线型包络线的主应力表达式为:
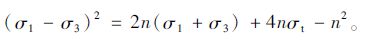
|
(4) |
在单轴压缩条件下,有σ3=0、σ1=σc,则式(4)变为:

|
(5) |
由式(5),可近似解得:

|
(6) |
式中σc为岩石单轴压缩强度。
2 基于极限分析的溶洞顶板冲切破坏 2.1 冲切破坏模型基本假定Jiang和Shen[10]在混凝土板冲切破坏研究中指出冲切破坏体并不是理想的圆锥台形,而是一条曲线;张慧乐等[8-9]所做的岩溶区嵌岩桩室内模型试验表明溶洞顶板冲切破坏时,破坏的冲切体近似圆锥台形,其母线方程是一条曲线。参考混凝土板冲切破坏理论研究和溶洞顶板冲切破坏的试验研究成果,并结合极限分析上限定理[15],假设的溶洞顶板冲切破坏模型如图 2所示,并对其作出如下假定:
(1) 溶洞顶板为轴对称固支圆板,厚度为h;桩端荷载为圆形均布荷载,二者中心轴线重合。
(2) 为了反映岩石非线性性质,采用莫尔二次抛物线型岩石破坏判据。
(3) 冲切破坏体表面光滑连续,破坏体的母线方程为待求曲线r(x)。
(4) 不考虑溶洞顶板的自重,在桩端荷载P作用下,溶洞顶板达到极限状态时,可分为3个区,见图 2。图 2中:A区与B区是刚性区,C区是塑性变形区。其中A区是一个轴对称的旋转体,以速度u竖直向下运动;C区是一个轴对称的旋转壳体,其厚度假定为一个非常小的值δ,而且其内部塑性变形必须满足塑性流动法则;d为桩径;d1为冲切破坏体的直径。

|
| 图 2 假定冲切破坏模型 Fig. 2 Failure model of assumed punching shear |
| |
2.2 基于功能原理极限荷载求解
如图 2所示,拉伸和剪切应变率分别为:

|
(7) |
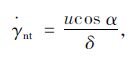
|
(8) |
式中,α为破坏面任意一点的切平面与速度u之间的夹角。二者之间的关系如图 1所示。
根据对称性可知,在切方向上没有变形,所以切应变率为:
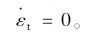
|
(9) |
而塑性区C处于平面应变状态,在环切向方向应变率为0,即:
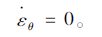
|
(10) |
由式(7)~(10)可得主应力方向上的应变:
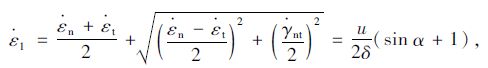
|
(11) |
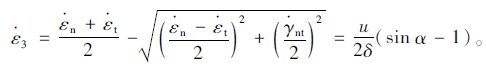
|
(12) |
根据塑性关联流动法则,如图 2所示,在σ-τ坐标中,屈服面任意一点的斜率为:
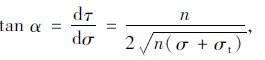
|
(13) |
由式(13)可得:
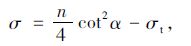
|
(14) |
将式(14)代入式(1)可得:
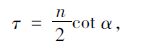
|
(15) |
将式(14)、(15)代入式(2)可得相应的主应力:
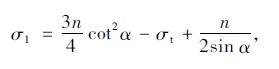
|
(16) |
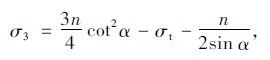
|
(17) |
作用于冲切体A上外力功率为:
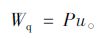
|
(18) |
可将冲切破坏体C看成一个轴对称旋转曲面,厚度为δ,对整个曲面S积分可得破坏面上的内能耗散率为:
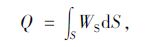
|
(19) |
式中,WS为塑性变形区单位体积的内能耗散率,表达式为:
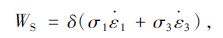
|
(20) |
将式(11),(12),(16),(17)代入式(20)可得:
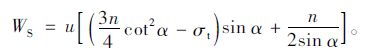
|
(21) |
根据上限定理,外功率等于内能耗散率,表达式为:
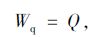
|
(22) |
将式(18),(19),(21)代入式(22)可得:
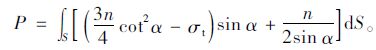
|
(23) |
由图(2)几何关系可得:
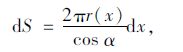
|
(24) |
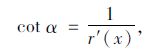
|
(25) |
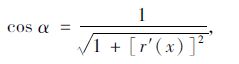
|
(26) |
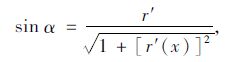
|
(27) |
式中,r′(x)为母线方程的求导,为方便书写,用r代替r(x), 并将式(24)~(27)代入式(23)可得:
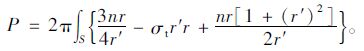
|
(28) |
令关于r′和r′(x)的函数F为:
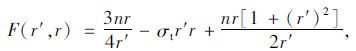
|
(29) |
则:
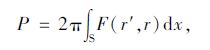
|
(30) |
将式(29)代入欧拉方程,F-r′Fr′=C中,则有:
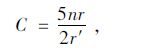
|
(31) |
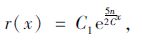
|
(32) |
式中,C,C1为待求参数,可由边界条件r(0)=d/2,r(h)=d1/2确定,其表达式分别为:
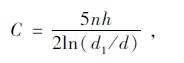
|
(33) |
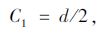
|
(34) |
将C,C1代回式(32)可得:
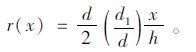
|
(35) |
由式(35)可知,冲切破坏体母线方程为一条对数螺旋线。
2.4 最小安全厚度求解将式(35)代入式(28)可得溶洞顶板极限承载力为:
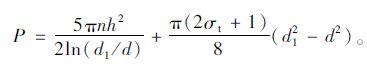
|
(36) |
由式(36)可知,溶洞顶板抗冲切极限荷载与岩石的抗压强度、抗拉强度、顶板厚度、桩径及冲切体底部直径相关。在嵌岩桩初步设计中,桩径大小为已知条件,需要求出溶洞顶板的最小安全厚度。将式(36)变形可得h的表达式为:
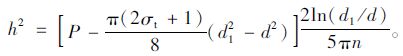
|
(37) |
由(37)式可知,溶洞顶板最小安全厚度与荷载、桩径及冲切体底部直径有关。在荷载和桩径一定的情况下,对式(37)微分求得d1的临界值,为:
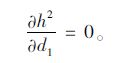
|
(38) |
通过式(38)求得d1,将d1代回式(37)可求得溶洞顶板最小安全厚度。
3 参数分析由式(37)推导出的溶洞顶板最小安全厚度h的表达式可知,h与参数n、直径比(d1/d)、抗拉强度σt有关,下面探讨各参数变化对计算结果的影响。
3.1 参数n的分析由式(6)n=σc2/2(σc+2σt)可知n与σc,σt有关,在工程实际中,可根据岩石力学参数手册取值[16]。为使分析简化,下面给出n与σc/σt的关系曲线。
由图 3可知,在保证抗拉强度不变时,参数n随抗压与抗拉强度比值σc/σt增大而增大;当σc/σt比值不变时,参数n随σt的增大而增大。

|
| 图 3 参数n随抗压与抗拉强度比值σc/σt变化关系图 Fig. 3 Curves of parameter n varying with ratio of compressive to tensile strengths σc/σt |
| |
3.2 最小安全厚度分析
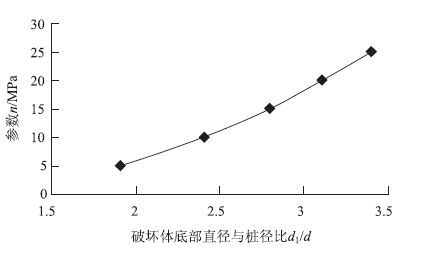
由式(38)可得到d1/d随n变化的关系曲线如图 4所示。
|
| 图 4 d1/d随参数n的变化关系图 Fig. 4 Curves of d1/d varying with parameter n |
| |
由图 4可知,d1/d随参数n的增大而非线性增大,而且随着n增大,d1/d增大变缓,并趋于某一极限值。这与文献[10]分析的结果一致,说明当参数n达到一定大小,溶洞顶板冲切破坏体母线方程将不再改变。再由图 3可知,在保证抗拉强度不变时,参数n随抗压与抗拉强度比值σc/σt增大而增大,因此d1/d也将随抗压与抗拉强度比值σc/σt增大而非线性增大。
4 工程算例 4.1 工程概况为验算本文的正确性,利用文献[17]提供的工程实例进行验算。本实例选取西江特大桥南引桥5号墩C桩桩基为研究对象。设计桩基溶洞顶板岩体参数如表 1所示。
| 参数 | σc/MPa | E/MPa | φ/(°) | c/MPa | σt/MPa | l/m | d/m | hr | H/m | 单桩设计承载力/N |
| 取值 | 63.6 | 10.63 | 55.1° | 0.75 | 0.306 | 39 | 3 | 2 | 4.9 | 14000 |
4.2 计算结果
对于极限状态,式(37)中P可为:

|
由式(6)求得n为:

|
由式(38)解得: d1/d=3.52, 由式(37)可得h=1.4 m。根据文献[2],安全系数取3,即得溶洞顶板最下安全厚度为4.2 m。
在该工程算例中,溶洞顶板的厚度为4.9 m,按本文方法求得溶洞最小安全厚度为4.2 m,满足溶洞顶板安全要求。同时按文献[12]的方法对该工程算例进行验算,安全系数取3,求得溶洞顶板最小安全厚度为4.56 m,满足溶洞顶板安全要求。因此,本文方法在评价实际工程安全稳定性方面是可行的。
5 结论(1) 本文参考较为成熟的混凝土板冲切破坏研究方法,基于功能原理,并结合莫尔二次抛物线岩石破坏判据,推导出了溶洞顶板冲切破坏体极限承载力计算公式,并进一步推导出了溶洞顶板最小安全厚度计算公式。
(2) 参数n随抗压与抗拉强度比值σc/σt增大而增大,d1/d随参数n的增大而非线性增大,从而得知d1/d随抗压与抗拉强度比值σc/σt的增大而非线性增大。
(3) 通过工程实例充分验证了最小溶洞顶板安全厚度计算公式的正确性,该公式参数选取简单,在工程实际验算溶洞顶板安全厚度运用简便,进一步完善了溶洞顶板冲切破坏的理论研究,对岩溶区嵌岩桩的初步设计有较高的实践价值。
| [1] | 黄生根, 梅世龙, 龚维明. 南盘江特大桥岩溶桩基承载特性的试验研究[J]. 岩石力学与工程学报 , 2004, 23 (5) : 809-813 HUANG Sheng-gen, MEI Shi-long, GONG Wei-ming. Testing Study on Bearing Behavior of Piles for Nanpan River Great Bridge in Karst Area[J]. Chinese Journal of Rock Mechanics and Engineering , 2004, 23 (5) : 809-813 |
| [2] | 黎斌, 范秋雁, 秦凤荣. 岩溶地区溶洞顶板稳定性分析[J]. 岩石力学与工程学报 , 2002, 21 (4) : 532-536 LI Bin, FAN Qiu-yan, QIN Feng-rong. Analysis on Roof Stability of Karst Cave in Karst Areas[J]. Chinese Journal of Rock Mechanics and Engineering , 2002, 21 (4) : 532-536 |
| [3] | 赵明华, 曹文贵, 何鹏祥, 等. 岩溶及采空区桥梁桩基桩端岩层安全厚度研究[J]. 岩土力学 , 2004, 25 (1) : 64-68 ZHAO Ming-hua, CAO Wen-gui, HE Peng-xiang, et al. Study on Safe Thickness of Rock Mass at End of Bridge Foundation's Pile in Karst and Worked-out Mine Area[J]. Rock and Soil Mechanics , 2004, 25 (1) : 64-68 |
| [4] | 赵明华, 陈昌富, 曹文贵, 等. 嵌岩桩桩端岩层抗冲切安全厚度研究[J]. 湘潭矿业学院学报 , 2003, 18 (4) : 41-45 ZHAO Ming-hua, CHEN Chang-fu, CAO Wen-gui, et al. Analysis for the Safe Terrane Thickness of Punching-shear Resistance at the End of Rock-socketed Piles[J]. Journal of Xiangtan Mining Institute , 2003, 18 (4) : 41-45 |
| [5] | 赵明华, 张锐, 胡柏学, 等. 岩溶区桩端下伏溶洞顶板稳定性分析研究[J]. 公路交通科技 , 2009, 26 (9) : 13-16 ZHAO Ming-hua, ZHANG Rui, HU Bo-xue, et al. Analysis of Stability of Cave Roof under Pile Tip in Karst Area[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (9) : 13-16 |
| [6] | 曹文贵, 程晔, 赵明华. 公路路基岩溶顶板安全厚度确定的数值流形方法研究[J]. 岩土工程学报 , 2005, 27 (6) : 621-625 CAO Wen-gui, CHENG Ye, ZHAO Ming-hua. Studies on Numerical Manifold Method for Determination of Safe Thickness of Karst Roof in Roadbed[J]. Chinese Journal of Geotechnical Engineering , 2005, 27 (6) : 621-625 |
| [7] | 赵明华, 蒋冲, 曹文贵. 岩溶区嵌岩桩承载力及其下伏溶洞顶板安全厚度的研究[J]. 岩土工程学报 , 2007, 29 (11) : 1618-1622 ZHAO Ming-hua, JIANG Chong, CAO Wen-gui. Study on Bearing Capacity of Rock-socked Piles and Safe Thickness of Cave Roofs in Karst Region[J]. Chinese Journal of Geotechnical Engineering , 2007, 29 (11) : 1618-1622 |
| [8] | 张慧乐, 张智浩, 王述红, 等. 岩溶区嵌岩桩的试验研究与分析[J]. 土木工程学报 , 2013, 46 (1) : 92-103 ZHANG Hui-le, ZHANG Zhi-hao, WANG Shu-hong, et al. Experimental Study and Analysis on Rock-socketed Pile in Karst Area[J]. China Civil Engineering Journal , 2013, 46 (1) : 92-103 |
| [9] | 张智浩, 张慧乐, 马凛, 等. 岩溶区嵌岩桩的破坏模式与工程设计探讨[J]. 岩石力学与工程学报 , 2013, 32 (S2) : 4130-4138 ZHANG Zhi-hao, ZHANG Hui-le, MA Ling, et al. Discussion on Failure Mode and Engineering Design of Rock-socketed Pile in Karst Area[J]. Chinese Journal of Rock Mechanics and Engineering , 2013, 32 (S2) : 4130-4138 |
| [10] | JIANG D H, SHEN J H. Strength of Concrete Slabs in Punching Shear[J]. Journal of Structural Engineering , 1986, 112 (12) : 2578-2591 |
| [11] | YANKELEVSKY D Z, LEIBOWITZ O. Punching Shear in Concrete Slabs[J]. International Journal of Mechanical Sciences , 1999, 41 (1) : 1-15 |
| [12] | 赵明华, 雷勇, 张锐. 岩溶区桩基冲切破坏模式及安全厚度研究[J]. 岩土力学 , 2012, 33 (2) : 524-530 ZHAO Ming-hua, LEI Yong, ZHANG Rui. Study of Punching Failure Mode and Safe Thickness of Pile Foundation in Karst Region[J]. Rock and Soil Mechanics , 2012, 33 (2) : 524-530 |
| [13] | 雷勇, 陈秋南, 马缤辉. 基于极限分析的桩端岩层冲切分析[J]. 岩石力学与工程学报 , 2014, 33 (3) : 631-638 LEI Yong, CHEN Qiu-nan, MA Bin-hui. Punching Analysis of Rock at Pile Tip Base on Limit Analysis[J]. Chinese Journal of Rock Mechanics and Engineering , 2014, 33 (3) : 631-638 |
| [14] | 刘佑荣, 唐辉明. 岩体力学[M]. 北京: 中国地质大学出版社, 1999 . LIU You-rong, TANG Hui-ming. Rock Mechanics[M]. Beijing: China University of Geosciences Press, 1999 . |
| [15] | CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier Science, 1975 . |
| [16] | 叶金汉. 岩石力学参数手册[M]. 北京: 水利电力出版社, 1991 . YE Jin-han. Rock Mechanical Parameters Manual[M]. Beijing: Water Resources and Electric Power Press, 1991 . |
| [17] | 汪华斌, 刘志峰, 赵文锋, 等. 桥梁桩基荷载下溶洞顶板稳定性研究[J]. 岩石力学与工程学报 , 2013, 32 (S2) : 3655-3662 WANG Hua-bin, LIU Zhi-feng, ZHAO Wen-feng, et al. Research on Stability of Cave Roof under Pile Loading in Bridge Construction Engineering[J]. Chinese Journal of Rock Mechanics and Engineering , 2013, 32 (S2) : 3655-3662 |
 2016, Vol. 33
2016, Vol. 33
