扩展功能
文章信息
- 黄侨, 万世成, 侯旭
- HUANG Qiao, WAN Shi-cheng, HOU Xu
- 桥梁预应力碳纤维板加固中的参数取值及损失计算方法研究
- Study on Parameter Determination and Calculation Method of Prestress Loss of Prestressed CFRP Plates in Bridge Reinforcement
- 公路交通科技, 2016, 33(9): 52-57
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(9): 52-57
- 10.3969/j.issn.1002-0268.2016.09.009
-
文章历史
- 收稿日期: 2015-12-17
2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710075, China
据统计,截至2014年年底,我国共有公路桥梁75.71万座,部分桥梁长时间超负荷服役,处于风险相对高发期。我国的桥梁建设已进入新建和改造维修并重的过渡阶段[1],桥梁加固技术方兴未艾。
国外自1984年开始研究纤维增强复合材料(Fibre Reinforced Polymer,简称FRP)加固法[2],而国内研究始于1997年[3]。在不到20年的时间里,FRP加固技术已由建筑结构拓展到桥梁领域,由碳纤维布发展到碳纤维板和预应力碳纤维板,并取得了一系列的研究成果。与粘贴纤维复合材料加固法不同,预应力碳纤维板加固法属于主动加固法,可以更高效地利用CFRP材料的抗拉强度;与传统体外预应力筋加固法相比,碳纤维板更易于形成黏结加固,可以很好地抑制裂缝并提高桥梁结构的极限承载力。
2002年,ACI颁布了《外贴FRP体系加固混凝土结构设计与施工指南》[4],标志着FRP加固技术趋于成熟。2014年,我国交通运输部计划对原《公路桥梁加固设计规范》进行修编,拟在“体外预应力加固法”一章中增补预应力纤维复合材料加固内容。本文提出的相关设计指标、计算系数取值及损失计算方法,可供桥梁加固设计及规范修编参考。
1 若干关键参数取值及计算方法 1.1 碳纤维板强度设计值的取值方法关于预应力碳纤维板抗拉强度设计值的取值,主要涉及材料在破坏阶段的强度利用率,且须避免出现具有脆性特征的剥离破坏。
根据湖南大学[5]和广西大学[6]的试验研究成果,当预应力碳纤维板加固梁发生破坏时,原梁内钢筋屈服,上缘混凝土压碎,在截面屈服破坏和极限破坏时不会出现界面剥离,碳纤维板的强度利用率可达到0.5ffk~0.7ffk,甚至更高。
《纤维增强复合材料建设工程应用技术规范》(GB 50608—2010)[7]提出的FRP强度设计值计算公式:ffd=ffk/(γfγe),纳入FRP材料分项安全系数和环境影响系数,前者对碳纤维板取1.25;后者对一般室外环境取1.1,对海洋环境及侵蚀性环境取1.2。由此可得碳纤维板的强度设计值为0.67ffk~0.73ffk。
《混凝土结构加固设计规范》(GB 50367—2013)[8]认为碳纤维板材的延性相对较差,对于重要结构尚需乘以重要性系数1.4以确保安全,其强度利用率大致为0.48ffk~0.5ffk。此结果与欧美等国按拉应变设计值εf与弹性模量设计值Ef乘积确定的设计应力值相当。
2006年,日本出台《后锚固连续纤维补强设计施工指针》[9],对连续纤维片材划分不同品系,以适应不同的加固需求。参考国产纤维复合材料规格并借鉴现行《公路桥梁加固设计规范》(JTG/T J22),建议对碳纤维板材的强度设计值分级取值:Ⅰ级1 200 MPa,Ⅱ级1 000 MPa,或统一采用0.5ffk。
1.2 梁侧预应力碳纤维板面积折减系数的计算方法若加固梁为混凝土T形截面梁,由于腹板较窄,梁底横向空间不足,往往需要在腹板底面和侧面同时布置预应力碳纤维板。
鉴于碳纤维板内纵向应力沿梁高方向的不均性,应对梁侧碳纤维板面积进行折减。文献[7]采用的折减系数计算式为:
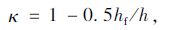
|
(1) |
式中,hf为侧面粘贴高度,即从碳纤维板上缘算起至梁受拉边缘的竖向距离;h为梁全截面高度。
应该注意,式(1)仅适用于粘贴纤维复合材料加固,前提是梁侧碳纤维板沿梁的下缘布置,有别于施加预应力的情况:在预应力碳纤维板加固中,需为锚固区切槽预留空间,并保证钢筋保护层厚度,梁侧碳纤维板通常距下缘有一定高度(图 1),尤其是采用钢筋骨架或叠放预应力钢束的肋板式结构。因此,建议以参数af替换式(1)中的hf。af的含义为梁侧碳纤维板重心轴至梁受拉边缘的竖向距离。

|
| 图 1 国外某侧贴预应力碳纤维板加固工程 Fig. 1 A foreign side-bonded prestressed CFRP plates reinforcement project |
| |
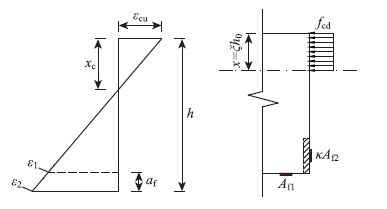
如图 2所示,根据平截面假定,折减系数κ可由以下方法确定:
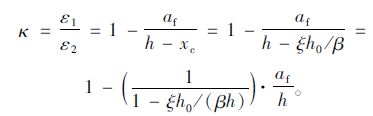
|
(2) |
|
| 图 2 梁侧碳纤维板面积折减系数κ计算图式 Fig. 2 Computing diagram of reduction factor κ for side-bonded CFRP plate area |
| |
旧桥加固工程中,混凝土强度等级通常低于C50,故取β=0.8,并引入调整系数η:
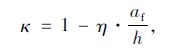
|
(3) |
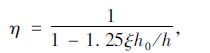
|
(4) |
式中,κ为梁侧碳纤维板面积折减系数;η为梁侧碳纤维板重心调整系数,与截面几何形状、材料强度及配筋率有关,应根据实际情况计算,其适用范围取决于超筋界限和加固效率两个因素。
对一般钢筋混凝土及预应力混凝土肋板式桥梁结构,可取h=1.1h0~1.2h0[10]。为防止脆性破坏,应满足相对受压区高度ξ≤ξb,对不同种类钢筋,ξb=0.53~0.62。
研究表明,当未加固梁的相对受压区高度大于ξb的0.8倍时,受弯承载力提高幅度有限且延性较小[7]。根据现行《公路桥梁加固设计规范》(JTG/T J22),受压区高度x不宜大于0.8ξbh0,基于近似算法[11],采用中点公式,取:
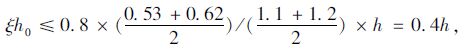
|
代入式(4),求得ηmax=2,即限制了预应力碳纤维板的最大加固用量,显然,η>1。综上,调整系数η的适用范围为1 <η≤2。
1.3 碳纤维板张拉控制应力取值方法预应力碳纤维板的张拉控制应力受到锚固能力、应力损失及其强度设计值的制约,取值存在差异性。国内相关加固试验大多采用缩尺试件,故张拉控制应力通常低于1 000 MPa。ACI 440.2R ERTA—2009[12]采用的控制应力为0.55ffu,相当于我国的0.55ffk。日本常用的有效紧张力一般可达到1 400 MPa,约占碳纤维板保证耐力的60%[13]。
《预应力碳纤维板锚固体系及设计施工应用指南》[14]对碳纤维板张拉控制应力的建议值为0.4ffk~0.65ffk。调研结果显示,工程实践中的常用值为0.5ffk,偶尔用到0.55ffk。基于延性设计理念,文献[6]建议预应力碳纤维板的张拉控制应力不宜大于0.5ffk,以保证构件抗弯破坏时碳纤维板具有大于1.5%的伸长率。
预应力碳纤维板加固混凝土梁的加固效果与预应力度及原梁配筋率有关。提高碳纤维板的预应力水平,可以提高构件在使用阶段的抗裂性和变形能力,但会降低其延性。现从提高碳纤维板的强度利用率及现有锚固装置的锚固能力两方面考虑,笔者建议张拉控制应力取σcon,f=0.5ffk为宜。
2 预应力碳纤维板预应力损失计算方法随着张拉、锚固过程和时间推移,碳纤维板中预拉应力会逐渐减少,主要来自锚具变形、碳纤维板与梁体混凝土间的温差、分批张拉引起的混凝土弹性压缩以及长期持荷下的应力松弛。本文预应力碳纤维板损失计算过程的参数编号与现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62)一致。
2.1 碳纤维板锚具变形损失计算方法当张拉结束并进行锚固时,锚具将承受巨大的压力并使锚具自身及垫板压密而变形,同时预应力碳纤维板向内回缩,进而引起应力损失,按式(5)计算:
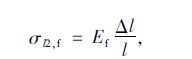
|
(5) |
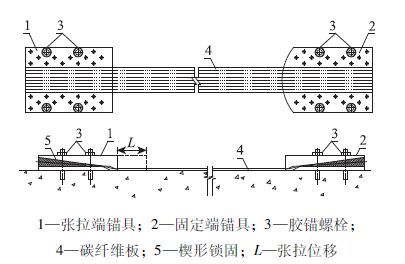
式中,Ef为碳纤维板的弹性模量;l为张拉端至锚固端之间的净距离;Δl为锚具变形和碳纤维板的回缩量,与锚具类型及其可靠性有关,应根据试验数据确定。目前,国内常用的预应力碳纤维板锚固装置主要为夹片式锚具,构造形式见图 3,如无实测资料,可取Δl=2 mm。对于其他专门研制的锚头,如Sika-StressHead[15],损失计算时锚具变形量应按其规定值取用。
|
| 图 3 夹片式锚具平面及纵剖面构造图 Fig. 3 Plan and section views of wedge-type anchor |
| |
2.2 碳纤维板温差损失计算方法
混凝土、CFRP两种材料的线膨胀系数相差较大,因此应考虑由季节温差造成的碳纤维板与梁体混凝土间的温差损失σl3,f:
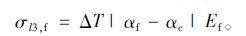
|
(6) |
线膨胀系数αf,αc需根据实测值确定,若难以实现,可近似取αf=1.0×10-6 ℃,αc=1.0×10-5 ℃。当环境升温时,两种材料共同伸长,而混凝土膨胀得更快,由于碳纤维板本身处于受拉状态,反而对保持预张拉力有利,故升温时不计温差损失;反之,当环境降温时,则应计入温差损失。所以,ΔT为年平均最低温度与预应力碳纤维板张拉、锚固时的温度差。
2.3 碳纤维板分批张拉损失计算方法加固中常需采用多片预应力碳纤维板,并分批张拉、锚固。由后张拉的碳纤维板所产生的混凝土弹性压缩变形将使先张拉并已锚固的预应力碳纤维板产生应力损失,即分批张拉损失,以σl4,f表示。
注意到对于不同批次的碳纤维板,对应的应力增量σl4,f可以是不同的。令m等于张拉碳纤维板的总批数,则第i批碳纤维板的σl4,f(i)为:
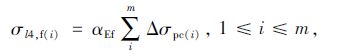
|
(7) |
式中,αEf为碳纤维板弹性模量与混凝土弹性模量的比值;Δσpc(i)为在计算截面上第i批碳纤维板重心处,由张拉第i+1批碳纤维板所产生的混凝土法向应力,按式(8)计算:
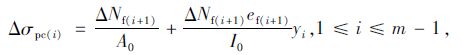
|
(8) |
式中,ΔNf(i+1)为第(i+1)批碳纤维板预加应力(扣除σl2,f)的合力;ef(i+1)为第(i+1)批碳纤维板预加力的作用点至加固梁换算截面重心轴的距离;yi为第i批碳纤维板重心至加固梁换算截面重心轴的距离。
由上可知,当i=1时,弹性压缩损失σl4,f(l)最大;当i=m时,则无弹性压缩损失,σl4,f(m)=0。
对矩形截面梁,可采用简化算法。假定各批碳纤维板张拉时,在先批碳纤维板重心处所产生的混凝土应力增量均相等,并以计算截面上全部预应力碳纤维板弹性压缩总损失的平均值作为各批碳纤维板的弹性压缩损失值,有:
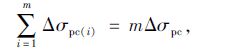
|
(9) |
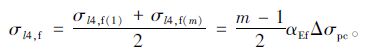
|
(10) |
式(9)~(10)的优点是可省去繁琐的计算过程,当张拉批次m较大时,体现得较为明显,但其仅适用于各批应力增量Δσpc(i)相差不大的情况。对于T形截面梁,由于腹板较薄,为避免出现旁弯,梁肋两侧的碳纤维板须采用同步、对称张拉工艺,而梁底碳纤维板则通常单片张拉,两者应力增量约呈2倍关系。这种情况下,不宜沿用上述简化,建议根据式(7)~(8)进行计算。
2.4 碳纤维板松弛损失计算方法Saadatmanesh等[16]试验证明,预应力CFRP筋的松弛损失主要与两个因素有关:时间t和初拉应力σcon,f。El-Hacha等[17]在研究预应力碳纤维布的应力松弛时,认为影响CFRP片材的因素与筋材一致。
文献[18]对CFRP板材的应力松弛做了研究,提出了包含上述两项影响因素的松弛损失计算式:
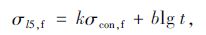
|
(11) |
式中系数k,b由回归分析解出。但试验采用的最大控制应力为0.3ffk,历时仅20 d;若考虑σcon,f=0.4ffk,t=2400h(100 d),并将r=σl5,f/σcon,f定义为预应力碳纤维板的松弛系数,代入式(11)后算得r=0.03。
文献[8]对松弛系数的建议值为r=2.2%,而OVM公司的松弛试验结果显示r=3.8%,且与施加的预应力水平有关。结合国内外现有研究成果,建议松弛损失按如下公式简化:
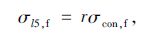
|
(12) |
式中,σcon,f为初拉应力;r为松弛系数,暂取3.0%,将来若有更多的试验数据可再作调整。
与体外预应力加固相类似[19],旧桥混凝土结构由于通常已使用了一定年限,其收缩、徐变已基本完成;此外,碳纤维板在长期预应力和外界荷载作用下的徐变量很小,对加固效果基本不产生影响[20],故不再考虑收缩、徐变损失σl6,f。
3 某RC简支梁桥预应力碳纤维板加固工程计算示例为检验上述参数取值及预应力损失计算方法的可行性和可靠性,笔者结合某钢筋混凝土简支梁桥加固工程进行试算分析,计算过程及结果如下。
3.1 设计资料及主梁内力(1) 简支梁跨径:标准跨径16 m,计算跨径15.6 m。
(2) 设计荷载:原桥设计荷载为汽-15级,挂-80,结构重要性系数γ0=1.0。
(3) 环境:桥址位于野外一般地区,Ⅰ类环境条件,年平均相对湿度为75%。
(4) 材料:原梁采用C30混凝土;架立钢筋为2根直径22 mm的HRB335钢筋,a′s=4.5 cm,受拉钢筋为10根直径28 mm的HRB335钢筋,as=15.5 cm,箍筋为直径8 mm的R235钢筋,间距14 cm,跨中双肢箍筋,梁端四肢箍筋。
(5) 设计要求:采用预应力碳纤维板加固法将原桥的设计荷载提高至公路—Ⅰ级。
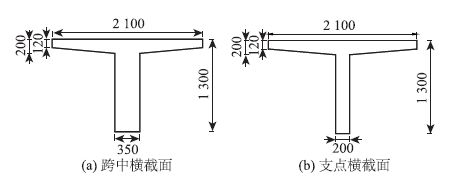
(6) 主梁尺寸:桥梁全宽8.4 m,净宽7.5 m,上部结构由4片T梁组成,横桥向对称布置,T梁翼板有效宽度为2 100 mm,跨中横截面、支点横截面构造如图 4所示。
|
| 图 4 T梁跨中横截面及支点横截面构造图(单位:mm) Fig. 4 Dimensions of cross-sections at mid-span and endpoint of T-beam (unit: mm) |
| |
(7) 主梁内力:考虑车道荷载对计算主梁的最不利荷载位置,并通过各主梁间的内力横向分布求得。桥梁冲击系数为1+μ=1.34,中梁的计算结果参见表 1。
| 截面位置 | 基本组合 | 短期组合 | ||
| 弯矩/(kN·m) | 剪力/kN | 弯矩/(kN·m) | 剪力/kN | |
| 支点截面 | 0 | 605 | 0 | 290.9 |
| 变截面 | 1 000 | 465 | 361 | 161 |
| 跨中截面 | 1 919.2 | 147 | 967.4 | 31.3 |
3.2 预应力碳纤维板用量估算
碳纤维板抗拉强度标准值ffk=2 400 MPa,张拉控制应力取σcon,f=0.5ffk=1200 MPa。安全起见,总损失量先按15%估计,则有效预应力估算值为σpe,f=0.85σcon,f=1020 MPa。
根据文献[19],选取预应力度λ=0.6,跨中截面消压弯矩M0=λMs=580.44 kN·m,截面下缘有效预压应力σpc=M0/W0b=5.08 MPa,所需预应力碳纤维板的总预拉力为:
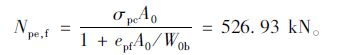
|
由此初步算得预应力碳纤维板的总面积:Apf=Npe,f/σpe,f=516.6 mm2,因此至少需采用3片100×2 mm2 碳纤维板,现拟在腹板底面腹板两侧各布置一片100×2 mm2碳纤维板。梁侧碳纤维板重心高度af=180 mm,锚固点距梁端2.5 m,布置形式参见图 5。
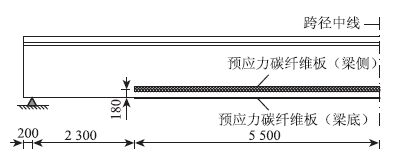
|
| 图 5 预应力碳纤维板纵向布置图(单位:mm) Fig. 5 Longitudinal layout of prestressed CFRP plates (unit: mm) |
| |
计算相对受压区高度时,偏安全地采用碳纤维板实际截面积: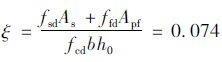
由式(3) ~(4),计算梁侧碳纤维板的两个重要系数:
重心调整系数: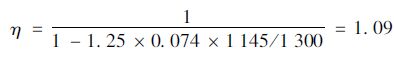
面积折减系数: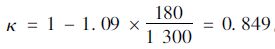
折减后的预应力碳纤维板总面积:Apf=Af1+κAf2=200+0.849×400=539.6 mm2。
3.3 预应力碳纤维板预应力损失计算预应力碳纤维板的预应力损失与施工工艺、材料性能及外界环境等有关,影响因素复杂,一般应根据试验数据确定,如无可靠试验资料,建议按本文第2节的方法计算。
加固设计中,应考虑4项预应力损失:锚具变形损失σl2,f、温差损失σl3,f、分批张拉损失σl4,f和松弛损失σl5,f。
两端锚具和碳纤维板的回缩量取Δl=2 mm;张拉时温度为14.8 ℃,施工地区属寒冷地区,按JTG D60—2015表 4.3.12-2取ΔT=24.8 ℃;张拉批次m=2,即先张拉梁底碳纤维板,再同步、对称张拉梁腹板两侧的碳纤维板;松弛系数采用r=0.03。按上述4项预应力损失计算方法求得的各项损失值见表 2。
| 位置 | 锚具变形 | 季节温差 | 分批张拉 | 长期松弛 | 总计 |
| 梁底(第1批) | 29.1 | 35.7 | 20.8 | 36.0 | 121.6 |
| 梁侧(第2批) | 29.1 | 35.7 | ― | 36.0 | 100.8 |
正常使用阶段,梁底、梁侧预应力碳纤维板中的永存预应力分别为: σpe,f(1)=1078.4 MPa,σpe,f(2)=1099.2 MPa。
综上,按本文的参数取值及损失计算方法,有效预应力占张拉控制应力的比例分别为89.9%和91.6%,这一结果与Kim等[21]建议的10%的预应力损失设计值基本相符。
研究报告[22]对类似桥梁结构采用体外预应力筋加固,在加固量和预应力水平相当的前提下,得到的有效预应力占88.4%(尚不计分批张拉损失)。不难看出,采用预应力碳纤维板加固法产生的预应力损失,相比于体外预应力筋加固法略偏小,文献[6]的试验数据亦证明了这一结论。
4 结论(1) 建议对桥梁加固用碳纤维板强度设计值分级取值:Ⅰ级1 200 MPa,Ⅱ级1 000 MPa,或统一采用0.5ffk。
(2) 侧贴CFRP板加固中的面积折减系数κ和重心调整系数η概念清晰,便于计算。
(3) 根据国内现有锚固体系和碳纤维板材,张拉控制应力建议取σcon,f=0.5ffk。
(4) 在钢筋混凝土桥梁加固中,对预应力碳纤维板应考虑4项预应力损失,即锚具变形损失、温差损失、分批张拉损失、松弛损失。采用体外预应力碳纤维板加固法产生的预应力损失一般在10%左右。
(5) 计算实例表明,本文建议的预应力碳纤维板加固设计的各项参数取值及损失计算方法简便可行,计算结果合理,可供钢筋混凝土桥梁加固设计参考。
| [1] | 张树仁. 桥梁病害诊断与加固设计[M]. 北京: 人民交通出版社, 2013 . ZHANG Shu-ren. Disease Diagnosis and Reinforcement Design of Bridges[M]. Beijing: China Communications Press, 2013 . |
| [2] | MEIER U. Carbon Fiber-Reinforced Polymers: Modern Materials in Bridge Engineering[J]. Structural Engineering International , 1992, 2 (1) : 7-12 |
| [3] | 岳清瑞, 陈小兵. 碳纤维材料(CFRP)加固修补混凝土结构新技术[J]. 工业建筑 , 1998, 28 (11) : 1-5 YUE Qing-rui, CHEN Xiao-bing. New Technology of Carbon Fiber Reinforced Plastics on Strengthening & Repairing Concrete Structures Structures[J]. Industrial Construction , 1998, 28 (11) : 1-5 |
| [4] | ACI 440.2R-02, Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures [S]. |
| [5] | 彭晖. 预应力碳纤维片材加固钢筋混凝土受弯构件的性能研究[D]. 长沙:湖南大学, 2006. PENG Hui. Study of Flexural RC Member Strengthened with Prestressed Carbon Fiber Reinforced Polymer Composites [D]. Changsha: Hunan University, 2006. http://cdmd.cnki.com.cn/article/cdmd-10532-2007020402.htm |
| [6] | 邓朗妮. 预应力碳纤维板加固受弯构件试验研究及理论分析[D]. 南宁:广西大学, 2010. DENG Lang-ni. Experimental Research and Theoretical Analysis of Flexural Members Strengthened with Prestressed CFRP Plates [D]. Nanning: Guangxi University, 2010. |
| [7] | GB 50608—2010, 纤维增强复合材料建设工程应用技术规范[S]. GB 50608—2010, Technical Code for Infrastructure Application of FRP Composites [S]. |
| [8] | GB 50367—2013, 混凝土结构加固设计规范[S]. GB 50367—2013, Code for Design of Strengthening Concrete Structure [S]. |
| [9] | 国住指第501号別添, あと施工アンカー·連続繊維補強設計·施工指針[S]. Country Living Finger No.501 Annex, Post-installed Anchor Continuous Fiber Reinforcement Design and Construction Guidelines [S]. |
| [10] | 叶见曙. 结构设计原理[M].3版. 北京: 人民交通出版社, 2014 . YE Jian-shu. Principle of Structure Design[M].3rd ed. Beijing: China Communications Press, 2014 . |
| [11] | FURMAN T T. Approximate Methods in Engineering Design[M]. LUO Ming-jun, et al. translated. Beijijng: New Times Press, 1985 . |
| [12] | ACI 440. 2R ERTA—2009, Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures [S]. |
| [13] | 濱田譲, 安森浩, 小林朗, 等. 炭素繊維プレート緊張材によるコンクリート構造物の補強[J]. コンクリート工学 , 2005, 43 (8) : 17-24 HAMADA Y, YASUMORI H, KOBAYASHI A, et al. Strengthening Method for Concrete Structures with Tensioned CFRP Plate[J]. Concrete Journal , 2005, 43 (8) : 17-24 |
| [14] | 柳州欧维姆结构检测技术有限公司. 预应力碳纤维板锚固体系及设计施工应用指南[M]. 柳州: 柳州欧维姆结构检测技术有限公司, 2013 . Liuzhou OVM Structure Inspection Technology Co., Ltd. Application Guide for Design and Construction of Prestressed CFRP Plates Anchorage System[M]. Liuzhou: Liuzhou OVM Structure Inspection Technology Co., Ltd., 2013 . |
| [15] | BASLER M, CLáNIN R, LIMIN W. Bridge Strengthening with Prestressted CFRP Plate Systems[C]//Metropolitan Habitats and Infrastructure. Shanghai: International Association for Bridge and Structural Engineering, 2004: 7-12. |
| [16] | SAADATMANESH H, TANNOUS F E. Relaxation, Creep, and Fatigue Behavior of Carbon Fiber Reinforced Plastic Tendons[J]. ACI Materials Journal , 1999, 96 (2) : 143-153 |
| [17] | EL-HACHA R, WIGHT R G, GREEN M F. Innovative System for Prestressing Fiber-reinforced Polymer Sheets[J]. ACI Structural Journal , 2003, 100 (3) : 305-313 |
| [18] | 黄金林, 黄培彦, 郑小红. 预应力碳纤维板加固钢筋混凝土梁预应力损失试验研究[J]. 建筑结构学报 , 2015, 36 (1) : 85-91 HUANG Jin-lin, HUANG Pei-yan, ZHENG Xiao-hong. Experimental Study of Prestress Losses of RC Beams Strengthened with Prestress FRP[J]. Journal of Building Structures , 2015, 36 (1) : 85-91 |
| [19] | 黄侨. 公路钢筋混凝土简支梁桥的体外预应力加固技术[M]. 北京: 人民交通出版社, 1998 . HUANG Qiao. External Prestress Strengthening Technology for Highway Reinforced Concrete Simply Supported Beam Bridges[M]. Beijing: China Communications Press, 1998 . |
| [20] | 尚守平, 张宝静, 吕新飞. 预应力碳纤维板加固梁桥长期徐变性能的试验研究[J]. 公路交通科技 , 2015, 32 (5) : 68-74 SHANG Shou-ping, ZHANG Bao-jing, LV Xin-fei. Experimental Study on Long-term Creep Behavior of Beam Bridge Strengthened with Prestressed CFRP Plate[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (5) : 68-74 |
| [21] | KIM Y J, GREEN M F, WIGHT R G. Bond and Short-term Prestress Losses of Prestressed Composites for Strengthening PC Beams with Integrated Anchorage[J]. Journal of Reinforced Plastics and Composites , 2009, 29 (9) : 1277-1294 |
| [22] | 黄侨. 公路桥梁体外预应力加固设计方法专题研究报告[R]. 南京:东南大学, 2008. HUANG Qiao. Research Report on Design Method of External Prestress Strengthening for Highway Bridges [R]. Nanjing: Southeast University, 2008. |
 2016, Vol. 33
2016, Vol. 33
