扩展功能
文章信息
- 武和全, 毛鸿锋, 曹立波
- WU He-quan, MAO Hong-feng, CAO Li-bo
- 汽车侧面碰撞车门可靠性优化设计
- Optimal Design of Reliability of Car Door against Side Impact
- 公路交通科技, 2016, 33(8): 146-151
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(8): 146-151
- 10.3969/j.issn.1002-0268.2016.08.022
-
文章历史
- 收稿日期: 2015-09-11
2. 长沙理工大学 工程车辆轻量化与可靠性技术湖南省高校重点实验室, 湖南 长沙 410004
2. Key Laboratory of Lightweight and Reliability Technology for Engineering Vehicle of Hunan Provincial Universities, University of Science and Technology, Changsha Hunan 410004;China
汽车侧面碰撞是发生频率最高的交通事故之一,在所有的交通事故中,侧面碰撞占32%,高于其他各类交通事故形态[1]。在交通事故所造成的人员伤亡中,侧面碰撞所造成的伤亡人数占总伤亡人数的30.1%,也是造成人员伤亡最多的交通事故形态。因此,研究汽车侧面碰撞的安全性具有重要意义。为减少交通事故中的乘员损伤,世界各国相继出台了相应的法规以规范汽车侧面碰撞的安全性。我国于2006年开始实施国家强制法规《汽车侧面碰撞的乘员保护》(GB20071—2006),该法规参照欧洲的ECER95标准执行。
乘用车侧面吸能空间小,乘员与门内板之间仅有20~30 cm的间隔,一旦受到来自侧面的撞击,乘员将受到强烈贯入的冲击载荷作用而受伤。车门作为重要的侧面结构,其侵入速度、侵入量与乘员的损伤有着直接的关系。国内外学者对此进行了大量研究,如徐涛[2]等人采用均匀试验设计方法对车门主要部件进行了抗撞性优化设计。王嵌[3]等人从轻量化的角度出发,对圆环、帽形和矩形3种不同截面的车门防撞杆进行了耐撞优化设计。Ali等[4]研究了6种材料对车门防撞杆性能的影响,并设计了一种新的防撞杆结构,通过车门侧碰吸能试验,结果表明:改变车门防撞杆的材料和几何形状可以显著增大车门的吸能量,减小车门的变形。
然而国内外对汽车侧面碰撞安全性优化设计[5-7]大多是以碰撞法规为基础来进行的,其忽略了实际交通事故发生时碰撞角度和碰撞速度的随机性,所以满足碰撞法规要求的车型,其侧碰安全性也并不是完全可靠的。此外,传统的确定性优化设计方法依照工程经验确定的单一的安全系数可能会偏大或偏小,从而造成汽车材料浪费或者结构不够安全。本文以美国交通事故调查统计数据[8]为基础,将可靠性理论应用于汽车车门的安全性研究,对车门部件进行优化设计。
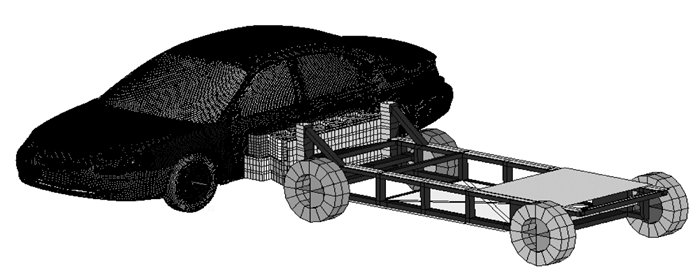
1 有限元模型的建立本文采用已经验证过的某轿车有限元模型(美国高速公路安全管理局NHTSA提供)进行车门可靠性优化设计,如图 1所示。该整车模型包括前后车门、B柱、地板、门槛梁等影响侧面碰撞安全性的主要部件以及发动机舱、动力总成、行驶系统等。整车模型总质量为2 609 kg。为了测量车门内板的侵入量,本文在左右车门之间建立弹簧离散单元,材料模型采用SDMAT1,弹簧刚度设为10-5N/mm。通过输出弹簧变形量获得车门内板侵入量。
|
| 图 1 侧面碰撞有限元仿真模型 Fig. 1 Finite element simulation model of side impact |
| |
在侧面碰撞安全性分析中,侧围侵入量、侵入速度和侵入形态是影响整车侧面碰撞安全性能的重要指标[9]。在以上轿车有限元模型中,以车门的内板、外板和防撞杆的材料和尺寸为设计变量,以实际交通事故中的碰撞角度和碰撞速度为随机变量,要求在碰撞过程中车门吸能量最大,同时车门的质量,车门内板最大侵入量,车门内板侵入速度满足设计要求。
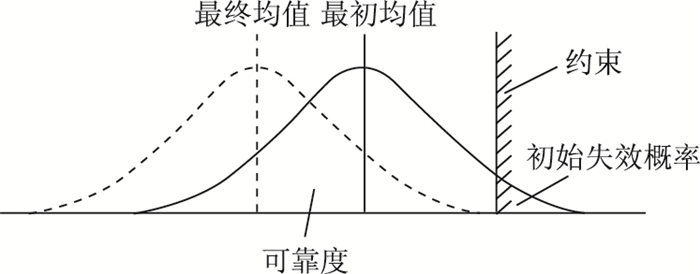
2 可靠性优化设计方法 2.1 失效率与可靠度可靠性优化设计就是把设计变量按一定的概率随机分布,最终使得产品的失效概率在一定范围内。因此,它是一种既能定量地评估产品的可靠性,又能使产品的性能获得最优解的优化方法[10]。图 2为可靠性优化示意图。
|
| 图 2 可靠性优化示意图 Fig. 2 Schematic diagram of reliability optimization |
| |
可靠性分析是进行可靠性优化设计的基础,可靠性分析的主要任务就是如何获得系统的或是结构组件的失效率。失效率是指在分析中违反约束条件的概率,结构可靠性被定义为满足约束条件的概率。本文拟采用一次二阶矩中心点法来计算,此方法计算简便,效率高。其基本思想为:首先将非线性功能函数在随机变量的平均值(中心点)处做泰勒级数展开并保留至一次项,然后近似计算功能函数的平均值与标准差。可靠指标直接用功能函数的平均值和标准差来表示。设x1, x2, …, xn是结构中n个相互独立的随机变量,其平均值为μxi,标准差为σxi(i=1, 2, …, n)。由这些随机变量表示的功能函数为Z=g(x1, x2, …, xn)。将功能函数Z在随机变量的平均值处展开为泰勒级数并保留至一次项,即:
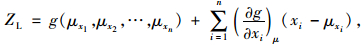
|
(1) |
式中,ZL为泰勒级数展开后的功能函数;g(x1, x2, …, xn)为功能函数;μxi为随机变量xi的均值。
对此,线性函数取平均值和方差得:
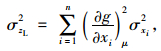
|
(3) |
式中,μzL为功能函数的平均值;σ2zL为功能函数的方差;σ2xi为随机变量的方差。
从而,可靠指标可表示为:
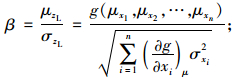
|
(4) |
结构的失效率为:
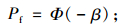
|
(5) |
可靠度R为:
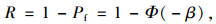
|
(6) |
式中Φ()为标准正态分布函数。
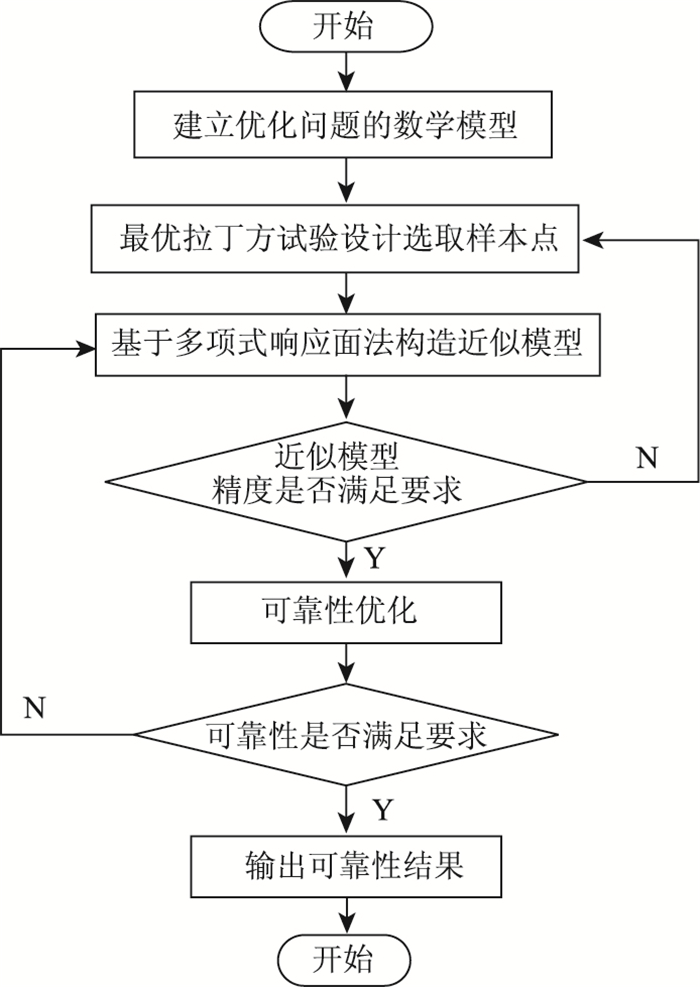
2.2 车门可靠性优化设计流程可靠性优化是一个双循环优化迭代过程,外循环为优化过程,内循环为可靠性分析过程。由于可靠性分析处于内循环中,如果直接基于有限元模型来进行可靠性分析,那么为了求解概率约束,每次优化过程都需要多次进行有限元计算,导致可靠性优化过程耗费大量的计算成本,从而陷入由计算复杂性引起的优化设计瓶颈。因此研究采用二次响应面近似模型代替整车有限元侧碰模型进行计算,从而大大减少了计算机高强度仿真计算的次数,提高了工作效率。车门可靠性优化设计问题具体流程如图 3所示。
|
| 图 3 车门可靠性优化设计流程图 Fig. 3 Flowchart of optimal design of car door reliability |
| |
3 车门可靠性优化 3.1 车门抗撞性试验设计
建立近似模型的前提是有一定数量的样本数据。在整个设计空间中选取有限数量的样本,要求尽可能全面反映设计空间特性,这就是试验设计。本文选用最优拉丁超立方试验设计,它改进了随机拉丁超立方设计的均匀性,使因子和响应的拟合更加精确真实,具有非常好的填充性与均衡性。
前面已经确定了试验设计的5个设计变量:车门内、外板的厚度(x1,x2),防撞杆的厚度(x3),车门内、外板的材料(x4,x5),厚度单位为mm,屈服强度单位为GPa。在实际的汽车碰撞过程中,碰撞情况是复杂多变的,造成的乘员损伤差别很大。本文根据美国交通事故文献[8]中的统计数据,对侧面碰撞过程中出现频率较大的情况进行分析,选取碰撞角度x6的范围为-30°~+30°, 碰撞速度x7的范围为40~60 km/h。假设所有变量都在均值附近服从正态分布。变量的取值如表 1所示。
| 变量 | 初始值 | 下限 | 上限 | 均值 | 标准差 |
| x1 | 0.75 | 0.6 | 1.2 | 0.9 | 0.05 |
| x2 | 1 | 0.8 | 1.5 | 1.15 | 0.1 |
| x3 | 1.8 | 1.5 | 2.5 | 2 | 0.15 |
| x4 | 0.24 | 0.2 | 0.35 | 0.275 | 0.025 |
| x5 | 0.344 | 0.25 | 0.4 | 0.325 | 0.02 |
| x6 | 0 | -30 | 30 | 0 | 9.9 |
| x7 | 50 | 40 | 60 | 50 | 3.2 |
3.2 响应面近似模型的构造
采用最优拉丁超立方试验设计,共选取了40组样本数据进行了试验,其中每组试验的吸能量E、内板最大侵入量X、内板最大侵入速度V和质量M均由LS-DYNA计算得出,如表 2所示。通过这40组样本数据及输出响应值构造了E,X,V,M的二次响应面近似模型。
| 组号 | 吸能E/kJ | 侵入量X/mm | 速度V/(m·s-1) | 质量M/kg |
| 1 | 2.986 7 | 212.731 | 13.143 5 | 13.59 |
| 2 | 3.176 3 | 220.180 | 11.916 2 | 13.41 |
| 3 | 3.476 1 | 190.077 | 10.952 0 | 15.50 |
| 4 | 2.434 4 | 163.015 | 8.511 6 | 11.25 |
| 5 | 2.496 5 | 148.986 | 8.630 4 | 16.61 |
| 6 | 2.921 0 | 177.504 | 10.605 5 | 14.46 |
| 7 | 3.367 5 | 260.903 | 13.960 6 | 11.24 |
| 8 | 3.792 3 | 244.891 | 14.206 2 | 17.29 |
| 9 | 3.111 1 | 168.498 | 9.105 2 | 16.99 |
| 10 | 3.524 0 | 226.960 | 13.657 4 | 13.30 |
| 11 | 3.423 9 | 211.276 | 12.443 1 | 16.87 |
| 12 | 4.037 9 | 315.588 | 16.489 7 | 11.71 |
| 13 | 3.709 5 | 255.178 | 13.228 0 | 14.57 |
| 14 | 2.631 1 | 169.477 | 9.516 8 | 13.30 |
| 15 | 2.910 6 | 190.939 | 10.613 9 | 12.13 |
| 16 | 3.970 1 | 267.078 | 13.984 0 | 15.53 |
| 17 | 3.588 9 | 288.732 | 14.152 1 | 12.69 |
| 18 | 3.009 3 | 198.440 | 12.761 6 | 12.30 |
| 19 | 4.092 8 | 246.218 | 12.897 4 | 13.53 |
| 20 | 3.747 1 | 285.853 | 13.664 3 | 13.83 |
| 21 | 3.039 6 | 187.226 | 12.345 5 | 15.37 |
| 22 | 4.396 4 | 310.188 | 17.051 5 | 15.77 |
| 23 | 3.149 4 | 200.765 | 10.544 3 | 15.60 |
| 24 | 4.130 8 | 329.289 | 17.166 3 | 12.39 |
| 25 | 4.558 9 | 291.669 | 14.591 2 | 17.34 |
| 26 | 3.830 9 | 297.061 | 16.513 4 | 12.34 |
| 27 | 3.399 1 | 217.942 | 11.997 2 | 17.45 |
| 28 | 2.703 4 | 171.846 | 9.672 2 | 13.80 |
| 29 | 3.783 3 | 252.403 | 14.906 7 | 17.09 |
| 30 | 3.120 0 | 214.031 | 11.758 9 | 10.81 |
| 31 | 4.073 0 | 299.868 | 15.244 2 | 14.51 |
| 32 | 3.095 6 | 202.508 | 10.993 8 | 12.84 |
| 33 | 3.826 8 | 259.465 | 13.728 7 | 15.43 |
| 34 | 3.153 7 | 195.179 | 10.744 3 | 16.63 |
| 35 | 4.140 2 | 297.235 | 15.446 2 | 14.19 |
| 36 | 3.707 7 | 251.940 | 13.415 4 | 15.76 |
| 37 | 3.035 6 | 190.510 | 11.543 4 | 14.02 |
| 38 | 4.343 2 | 293.391 | 15.692 0 | 16.38 |
| 39 | 3.687 9 | 252.617 | 14.470 6 | 15.24 |
| 40 | 2.439 8 | 158.631 | 8.851 4 | 14.25 |
因为汽车碰撞问题的高度非线性,所以难以建立目标和设计变量之间的显性函数关系。基于多项式的响应面近似模型可以很好地解决这个问题。定义二阶多项式响应面的计算如式(7)所示。
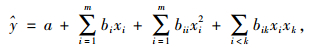
|
(7) |
式中,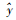
3.3 可靠性优化
相关研究表明[12],为了达到轻量化、高刚度以及吸能量最大的目的,建立数学模型时,质量、最大侵入量及最大侵入速度这几个约束值可以等于或略小于初始值。建立车门可靠性优化数学模型如式(10)所示。
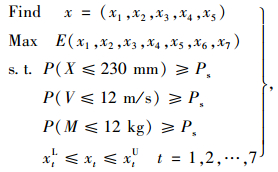
|
(10) |
式中,Ps为可靠度,选取可靠度为0.95进行研究;xtL和xtU为变量的上、下界。
3.4 优化结果分析对车门进行可靠性优化设计并与不考虑可靠度的确定性优化设计结果进行比较,如表 4所示。从表中可以看出,相比于初始设计,确定性优化使得设计变量x4非常接近边界约束值,一旦由于加工制造等不确定性因素使得设计变量产生轻微波动,就会使优化结果超出约束范围而不满足边界约束条件,导致确定性优化结果失败。因此,确定性优化的结果是不可靠的,需要进行可靠性优化设计。
| 设计变量 | 初始设计 | 确定性优化设计 | 可靠性优化设计 |
| x1 | 0.75 | 0.623 | 0.678 |
| x2 | 1 | 0.847 | 0.819 |
| x3 | 1.8 | 1.516 | 1.528 |
| x4 | 0.24 | 0.2 | 0.342 |
| x5 | 0.344 | 0.376 | 0.285 |
表 5给出的是输出响应的优化结果值。从表中可以看出,相比于初始设计,确定性优化的质量M明显减少,吸能E也略有增加,但是侵入量X和侵入速度V比较接近约束边界,它们的可靠度仅为0.617和0.681,因此确定性优化不能满足可靠性设计要求。相比于初始设计,可靠性优化设计使得侵入量X减少了14.1%,侵入速度V减少了22.5%,质量M减少了14.6%,而且吸能E还略微增加了2.3%。相比于确定性优化,虽然可靠性优化使得质量M略有增加,但是侵入量X和侵入速度V却都有所减少且远离约束边界,它们的可靠度分别为0.957和0.963,满足可靠性设计要求。
| 输出响应 | 初始设计 | 确定性优化设计 | 可靠性优化设计 | ||
| 最优值 | 可靠度 | 最优值 | 可靠度 | ||
| 吸能E/kJ | 3.55 | 3.598 | — | 3.63 | — |
| 侵入量X/mm | 250.327 | 226 | 0.617 | 214.975 | 0.957 |
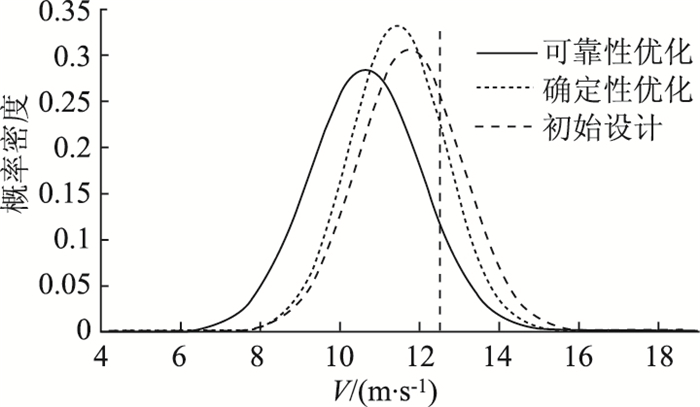
| 速度V/(m·s-1) | 13.614 | 11.442 | 0.681 | 10.556 | 0.963 |
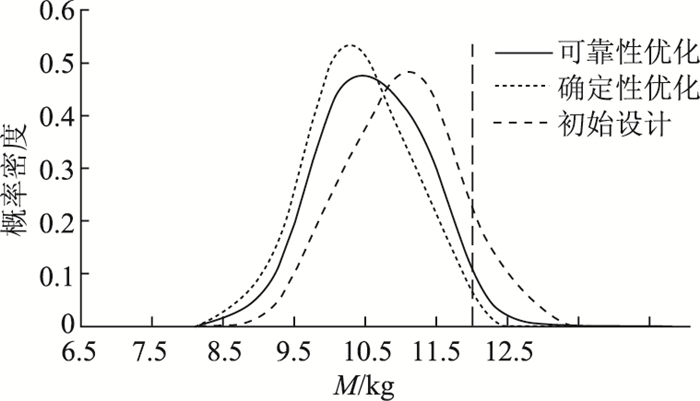
| 质量M/kg | 12.37 | 10.4 | 0.988 | 10.57 | 0.977 |
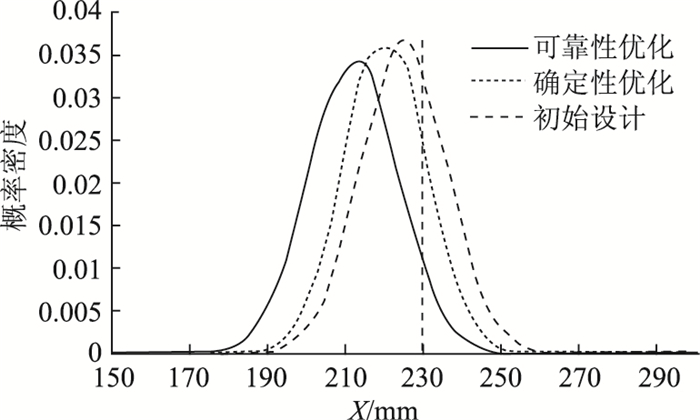
图 4~图 6为输出响应X,V,M的概率密度分布图,图中竖线为约束边界条件。从图中可以看出,响应X,V初始设计和确定性优化设计的可靠度都比可靠性优化设计低,响应M可靠性优化设计的可靠度虽然略低于确定性优化设计,但明显高于初始设计且满足可靠性要求。因此,可靠性优化设计使得车门满足可靠性要求。
|
| 图 4 侵入量X概率密度分布图 Fig. 4 Probability density distribution of X |
| |
|
| 图 5 侵入速度V概率密度分布图 Fig. 5 Probability density distribution of V |
| |
|
| 图 6 质量M概率密度分布图 Fig. 6 Probability density distribution of M |
| |
4 结论
本文以美国汽车侧面碰撞交通事故统计数据为基础,在充分考虑实际情况下碰撞角度和碰撞速度随机性的情况下,选取对车门性能有重要影响的车门厚度和材料为设计变量,将试验设计、响应面模型、可靠性理论和优化算法相结合,对车门的可靠性进行分析,得出了最优的内板、外板及防撞杆的各项参数。研究结果表明,侧面碰撞可靠性优化设计不仅使得车门质量减少,而且可以实现在不同的碰撞边界条件下,汽车车门均满足侧面碰撞的安全性设计要求。本文的研究方法和成果为开发满足实际道路交通状况的汽车侧面碰撞安全性设计评价标准提供了参考。
| [1] | 国家统计局. 中国统计年鉴(2013)[M]. 北京: 中国统计出版社, 2013 . National Bureau of Statistics. China Statistical Yearbook, 2013[M]. Beijing: China Statistics Press, 2013 . |
| [2] | 徐涛, 郝亮, 徐天爽, 等. 轿车侧碰中车门抗撞性的快速优化[J]. 吉林大学学报:工学版 , 2012, 42 (3) : 677-682 XU Tao, HAO Liang, XU Tian-shuang, et al. Fast Crashworthiness Optimization of Car Door during Side Collision[J]. Journal of Jilin University:Engineering and Technology Edition , 2012, 42 (3) : 677-682 |
| [3] | 王嵌, 杨济匡, 郭杰. 轿车车门防撞杆结构优化的研究[J]. 汽车工程 , 2010, 32 (12) : 1047-1052 WANG Qian, YANG Ji-kuang, GUO Jie. A Study on the Structural Optimization of Side Door Bar for a Passenger Car[J]. Automotive Engineering , 2010, 32 (12) : 1047-1052 |
| [4] | GHADIANLOU A, ABDULLAH S B. Crashworthiness Design of Vehicle Side Door Beams under Low-speed Pole Side Impacts[J]. Thin-Walled Structures , 2013, 67 (2) : 25-33 |
| [5] | 苏成谦, 吕振华. 轿车车身结构侧向耐撞性的有限元分析[J]. 汽车工程 , 2007, 29 (11) : 964-969 SU Cheng-qian, LV Zhen-hua. Finite Element Analysis on the Lateral Crashworthiness of Car Body Structure[J]. Automotive Engineering , 2007, 29 (11) : 964-969 |
| [6] | ZAREI H R, KROGER M. Multiobjective Crashwor-thiness Optimization of Circular Aluminum Tubes[J]. Thin-Walled Structures , 2006, 44 (3) : 301-308 |
| [7] | 李铁柱, 李光耀, 高晖, 等. 基于可靠性优化的汽车乘员约束系统的性能改进[J]. 中国机械工程 , 2010, 21 (8) : 993-999 LI Tie-zhu, LI Guang-yao, GAO Hui, et al. Performance Improvement of Occupant Restraint System Based on Reliability Optimization Method[J]. China Mechanical Engineering , 2010, 21 (8) : 993-999 |
| [8] | KUSANO K D, GABLER H C. Automated Crash Notification:Evaluation of In-vehicle Principal Direction of Force Estimations[J]. Transportation Research Part C:Emerging Technologies , 2013, 32 (32) : 116-128 |
| [9] | 胡玉梅, 姜亚洲, 禹慧丽, 等. 轿车侧面碰撞乘员舱分区刚度优化与匹配研究[J]. 汽车工程 , 2014 (8) : 950-956 HU Yu-mei, JIANG Ya-zhou, YU Hui-li, et al. A Study on the Optimization and Matching of Subarea Stiffness in the Passenger Compartment of a Car for Side Impact[J]. Automotive Engineering , 2014 (8) : 950-956 |
| [10] | 张勇, 徐西鹏, 杨永柏, 等. 基于不确定性准则的薄壁管耐撞可靠性设计[J]. 中国机械工程 , 2012, 23 (21) : 2612-2616 ZHANG Yong, XU Xi-peng, YANG Yong-bai, et al. Crashworthiness Reliability Design of Thin-walled Tube Based on Uncertainly Criterion[J]. China Mechanical Engineering , 2012, 23 (21) : 2612-2616 |
| [11] | 鲍诺, 王春洁, 赵军鹏, 等. 基于响应面法的结构动力学模型修正[J]. 振动与冲击 , 2013, 32 (16) : 54-58 BAO Nuo, WANG Chun-jie, ZHAO Jun-peng, et al. Based on the Response Surface Method of Structure Dynamic Model Updating[J]. Journal of Vibration and Shock , 2013, 32 (16) : 54-58 |
| [12] | 李亦文, 徐涛, 徐天爽, 等. 车身低速碰撞吸能结构的优化设计[J]. 北京理工大学学报 , 2010, 30 (10) : 1175-1179 LI Yi-wen, XU Tao, XU Tian-shuang, et al. Body Low-speed Collision Energy Absorption Structure Optimization Design[J]. Journal of Beijing Institute of Technology , 2010, 30 (10) : 1175-1179 |
 2016, Vol. 33
2016, Vol. 33
