扩展功能
文章信息
- 郑来, 邓晓庆, 孟祥海
- ZHENG Lai, DENG Xiao-qing, MENG Xiang-hai
- 基于PET极值统计的高速公路车道变换行为安全性研究
- Study on Safety of Lane Changing Behaviours on Expressway Based on PET Extreme Statistics
- 公路交通科技, 2016, 33(8): 120-126
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(8): 120-126
- 10.3969/j.issn.1002-0268.2016.08.018
-
文章历史
- 收稿日期: 2015-07-17
车道变换是高速公路上一种较为常见的车辆行驶方式,同时也是诱发交通事故的一个重要原因。Guo等人的研究指出2007年在美国发生的与车道变换相关的交通事故占交警记录的交通事故总数的5%,占伤亡事故总数的0.5%[1]。徐慧智等人的研究也指出在中国与车道变换行为相关的交通事故约占交通事故总数的30%[2]。因此,开展与车道变换行为安全性相关的研究对进一步改善道路安全水平具有重要意义。
由于交通事故的发生具有强随机性和稀少性,累积得到满足统计分析要求的事故数据往往需要较长的周期。为了提高安全分析的时效性,学者们相继提出了多种用于替代或作为事故数据补充的交通安全分析技术,交通冲突就是其中最具代表性的一种技术[3-6]。其中,作为一种较为常用的交通冲突衡量指标,后侵入时间(Post encroachment time,PET)的可测性和可靠性得到了普遍的认可[7-9],但PET也面临着冲突阈值难以界定、有效性验证困难等问题[10]。因此,如何更好地利用PET数据进行安全分析便成为研究的重点之一。
极值理论作为一种分析极小概率事件分布的理论,也被Campbell等人较早地应用于交通安全分析[11],之后Tarko和Songchitruksa对其进行进一步研究和论证[12-13]。其将交通事故视为交通事件范围内的极值事件,并应用极值理论分析了交叉口范围内的PET与交通事故之间的关系。上述研究中,极值理论的应用虽然均以交叉口的PET数据为基础,其研究思路和方法为本文开展的研究提供了借鉴和参考。
本文将以高速公路车道变换过程中的PET数据为基础,探讨基于PET的极值统计模型的构建和其在高速公路交通安全分析方面的应用,以期为交通冲突技术的完善和交通安全分析方法的扩展提供思路。
1 PET的界定与分析 1.1 数据来源本文数据来自于广东省交通运输厅科技项目《基于全社会成本的公路设计方案评价技术研究》中的专题五“高速公路设计方案安全性评价研究”。该课题共收集到了广湛高速公路开平至阳江段、粤赣高速公路上陵至埔前段以及京珠高速公路粤北段等3条高速公路共56个分方向路段的交通运行状况视频和交通事故历史数据。
根据各路段视频质量和视频长度,最终选用了29个分方向路段,每个路段的视频长度约为3 h,记录时间均为上午08:30—11:30或下午14:00—17:00。通过对视频的处理和分析,可以得到路段长度、交通流量、车道变换次数等信息,其中各路段观测时段内的流量在800~3 026 veh/h之间,并且京珠高速公路粤北段各路段的流量较小但大型车比例较高,广湛高速公路开平至阳江段和粤赣高速公路上陵至埔前段交通流量较大但大型车比例较小。
交通事故数据来自于高速公路的路政管理部门,广湛高速公路开平至阳江段和粤赣高速公路上陵至埔前段的事故年限为2007—2012年,事故总数分别为1 831次和1 438次;京珠高速公路粤北段的事故年限为2005—2008年,事故总数为2 075次。通过对事故发生地点的分析,得到发生在调查路段的事故总数为98次。在剔除了发生在夜晚时段的交通事故和由爆胎、车辆失火等与车道变换行为无关的事故后,最后得出在29个路段上共有45次有效交通事故。
1.2 PET的界定车道变换过程中的PET是指跟随车辆的头部到达侵入线的时间与先导车辆的尾部离开侵入线的时间之差,其中一辆车为车道变换车辆。侵入线是垂直于车道分界线并经过车道分界线与车辆变道轨迹交点的虚拟直线。利用VirtualDub软件逐帧处理视频并测量PET,测量精度为0.04 s(每25帧为1 s),测量过程如图 1所示。在第38 925帧,位于原始车道的先导车辆(红车)尾部离开侵入线;在第38 951帧,即将驶入目标车道的跟随车辆(即车道变换车辆,黑车)头部到达侵入线。因此,这两辆车之间的PET=(38 951-38 925)/25=1.04 s。

|
| 图 1 PET测量示意图 Fig. 1 Illustration of PET Measuring |
| |
在双向四车道高速公路上,一辆变道车辆的周围最多可能有4辆其他车辆,即每个车道上可能有一辆先导车辆和跟随车辆(假设不存在其他车辆与变道车辆绝对平行行驶的情况)。因此,每一个车道变换行为最多可测出4个PET值,本文选取其中的最小值作为该车道变换行为的PET。
一般将PET小于某一临界值的车道变换事件定义为车道变换冲突。如果参照SSAM模型[7],将PET≤3.0 s的事件界定为冲突,那么29个路段上共有车道变换冲突3 446次。然而,分析表明各路段车道变换冲突次数与交通事故次数的相关性较低,皮尔逊相关性系数仅为0.24(显著性水平p=0.22),这说明以PET=3.0 s所界定的交通冲突与交通事故之间并没有很好的相关性,因此该交通冲突或许是简单的通过选择某一PET临界值而界定出的交通冲突,并不能直接反映出一个路段的安全状况。鉴于此,本文提出应用极值统计方法对PET所蕴含的安全信息进行进一步挖掘和分析。
2 极值理论模型极值理论主要研究随机过程中极值事件的发生概率和统计分布[14]。根据极值确定方法的不同,分为区组极值模型和超阈值模型。有关区组极值模型和超阈值模型的对比研究表明,超阈值模型在极值提取和可靠度方面均优于区组极值模型[15]。因此,本文选用超阈值模型进行PET极值分析。
2.1 超阈值模型及广义帕累托分布假设X1,X2,…,Xn是来自分布函数F的一系列独立样本,将值大于某一阈值的样本视为极值样本的方法即为超阈值方法。Pickands证明了当阈值足够大时,超阈值极值服从广义帕累托分布(Generalized Pareto Distribution, GPD)[16]。
在集合{x:x>0且1+ξxσ>0}中,GPD的形式如下:
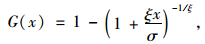
|
(1) |
式中,σ为尺度参数;ξ为形状参数。当ξ=0时,式(1)取ξ→0的极限形式,即:
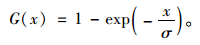
|
(2) |
GPD分布的对数似然函数为:
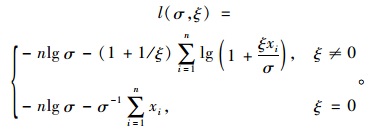
|
(3) |
在极值理论中,重现水平(Return Level)是一个非常重要的概念。对应于重现期T=1/p的重现水平zp的定义公式如下[14]:
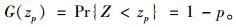
|
(4) |
重现水平zp可以有以下两种理解方式:以百年一遇洪水值(即重现期为100 a的洪水水位重现水平)为例,如果一条河流的重现水平值为z=0.0110 m,则表示该河流水位超过10 m的情况每100 a会出现一次,或每一年该河流水位超过10 m的概率为0.01。
在极值样本满足GPD分布的前提下,重现水平的计算公式如下[14]:

|
(5) |
式中,u为阈值;σ和ξ为GPD分布的参数;T为重现期;n为观测时段内的样本总量; λu为观测时段内超过阈值样本所占的比例。
3 车道变换PET的极值统计模型 3.1 模型构建的基本原理从车道变换PET的角度来看,PET值越小表明两辆车之间越接近,发生碰撞的可能性也就越高。当PET≤0时,两辆车刚好或已经碰撞,交通事故发生。因此,安全分析的焦点可以理解为车道变换事件中较为少见的PET≤0事件的概率分布情况。
从极值理论的角度来看,虽然超阈值模型能够描述极值事件的概率分布,但仅限于大于某一阈值的极值事件。
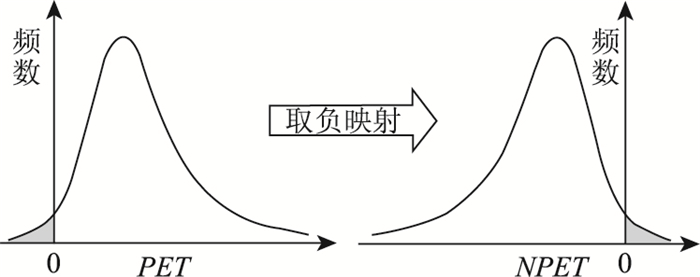
为了使所构建的超阈值模型能够反映出车道变换事件中PET≤0事件的概率分布情况,本文引入了PET取负映射,如图 2所示。当PET取负映射为NPET后,NPET≥0(即PET≤0)即意味着已发生交通事故。因而,可以通过建立基于NPET的超阈值模型达到相应的安全分析目标。
|
| 图 2 取负映射概念图 Fig. 2 Conceptual diagram of negated mapping |
| |
根据2.1节介绍的超阈值理论,基于NPET的超阈值模型可以表示为:
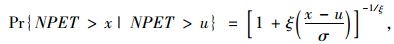
|
(6) |
式中,u,σ和ξ为模型参数。该模型说明当阈值u足够大时,超过阈值的NPET(或对应的小于-u的PET)的发生概率服从广义帕累托分布。
3.2 阈值确定超阈值模型构建最关键的是合理确定阈值u,进而才能对其他两个参数(σ, ξ)进行估计。如果阈值过大,会导致极值样本量较少,使得参数估计结果的方差偏大;如果阈值过低,非极值事件会被视为极值样本,违背了极值理论的渐进原则,导致产生有偏估计。因此,需要合理地确定阈值,以达到模型估计方差与偏差的平衡。
本文选用极值分析领域较为常用的图解法进行阈值确定,即通过平均剩余寿命图和阈值稳定性分析图来确定阈值。图解法的基本原理为:如果超出阈值u0的样本服从广义帕累托分布,那么对任意一个阈值u>u0,其阈值u超出值同样服从广义帕累托分布。因此,对于平均剩余寿命图,当u>u0时E(X-u|X>u)应是阈值u的线性函数;而对于阈值稳定性分析图,广义帕累托模型的形状参数ξ和修正后的尺度参数σ*=σu-ξu应基本是恒定的。
根据上述基本原理,利用图解法确定阈值的基本步骤为:(1) 依据平均剩余寿命图,选择一个阈值范围R1,该范围内的平均剩余寿命线近似线性变化;(2) 依据阈值稳定性分析图,确定一个范围R2,该范围内修正后的尺度参数和形状参数能够基本不随阈值u的变化而变化;(3) 取上述两个范围的交集,R=R1∩R2,并以集合R的上确界u+作为最终阈值。
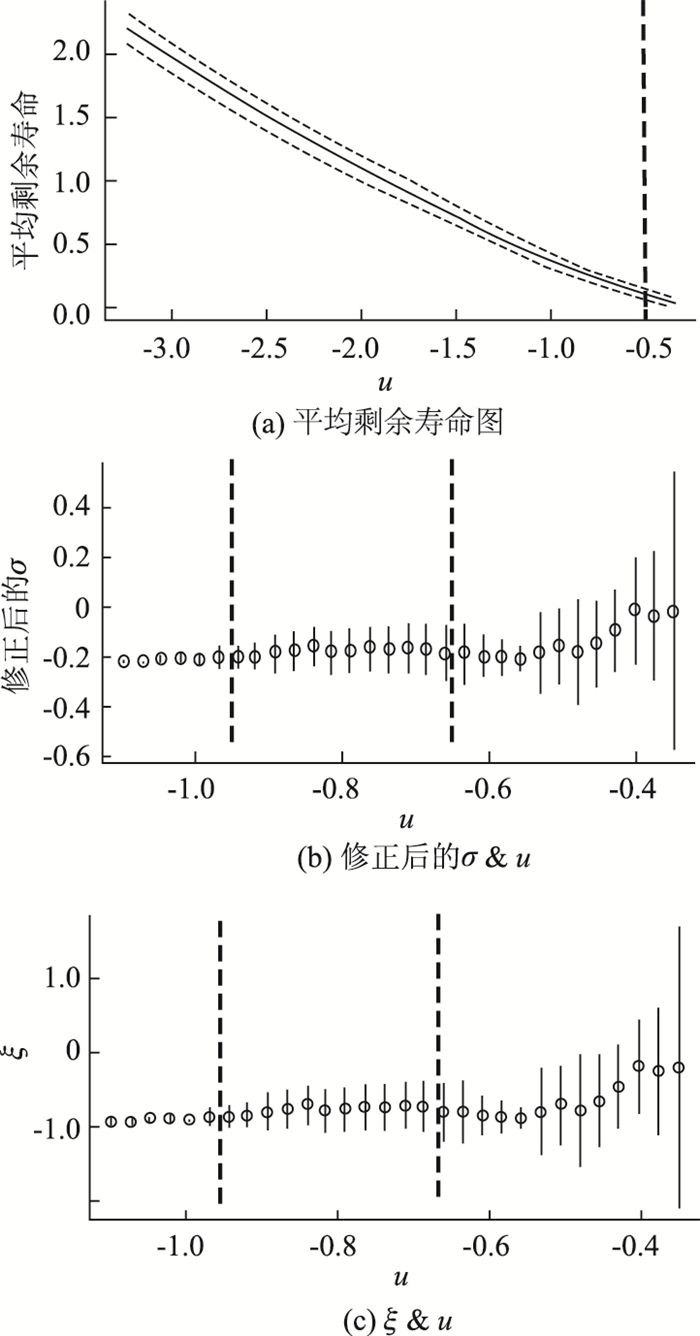
以开阳高速公路上的调查路段KY3K_L为例,该路段上车道变换PET数量为103个,其中,NPET最大值为-0.20 s。如图 3所示,当u≤-0.5 s(即R1=[-3.0,-0.5])时,平均剩余寿命线几乎呈线性;在R2=[-0.95, -0.65]的范围内,修正后的尺度参数和形状参数基本保持不变。因此最终的阈值范围R=[-0.95, -0.65],而最终确定的该路段的阈值为-0.65。
|
| 图 3 阈值选择的图解分析图 Fig. 3 Graphical diagnostics for threshold selection |
| |
3.3 模型参数估计
在利用图解法依次确定了各个路段的阈值之后,即可进行模型其他两个参数(σ, ξ)的估计。本文选取的是极大似然估计方法(Maximum Likelihood Estimation, MLE),使用的是R软件中的“extRemes”极值分析工具包[17]。29个路段所对应的超阈值模型的阈值确定结果以及尺度参数和形状参数的估计结果如表 1所示。
| 路段编号 | 车道变换次数 | PET个数* | 阈值u | 阈值超出量 | nllh | 参数估计值 | |||
| 尺度参数σ | SE(σ) | 形状参数ξ | SE(ξ) | ||||||
| JZ3G_L | 165 | 113 | -1.20 | 40 | -6.70 | 0.427 | 0.116 | -0.315 | 0.228 |
| JZ4B_R | 143 | 97 | -1.10 | 30 | -6.20 | 0.685 | 0.167 | -0.827 | 0.143 |
| JZ4G_L | 122 | 78 | -1.20 | 32 | -2.70 | 0.663 | 0.136 | -0.671 | 0.158 |
| KY1Y_R | 416 | 378 | -0.45 | 41 | -48.20 | 0.200 | 0.040 | -0.436 | 0.150 |
| KY1Y_L | 119 | 97 | -1.00 | 35 | -5.00 | 0.575 | 0.097 | -0.554 | 0.118 |
| KY2K_R | 192 | 170 | -0.70 | 43 | -35.90 | 0.256 | 0.045 | -0.473 | 0.116 |
| KY2K_L | 136 | 119 | -0.75 | 35 | -24.50 | 0.380 | 0.079 | -0.730 | 0.172 |
| KY2Y_R | 220 | 189 | -0.60 | 38 | -31.30 | 0.198 | 0.049 | -0.458 | 0.182 |
| KY2Y_L | 134 | 92 | -1.00 | 33 | -9.00 | 0.725 | 0.027 | -0.953 | 0.027 |
| KY3K_R | 154 | 136 | -0.65 | 33 | -24.30 | 0.410 | 0.026 | -0.867 | 0.069 |
| KY3K_L | 127 | 103 | -0.80 | 31 | -18.50 | 0.380 | 0.077 | -0.609 | 0.147 |
| KY3Y_R | 111 | 99 | -0.65 | 33 | -28.60 | 0.271 | 0.063 | -0.560 | 0.181 |
| KY4K_L | 56 | 43 | -1.45 | 33 | 11.10 | 1.107 | 0.248 | -0.756 | 0.194 |
| KY5K_R | 71 | 68 | -0.85 | 34 | -13.80 | 0.462 | 0.114 | -0.634 | 0.208 |
| KY6K_R | 115 | 108 | -0.70 | 34 | -26.40 | 0.345 | 0.073 | -0.736 | 0.176 |
| KY6K_L | 93 | 84 | -0.80 | 33 | -19.90 | 0.426 | 0.088 | -0.749 | 0.171 |
| KY6Y_R | 114 | 103 | -0.65 | 43 | -34.20 | 0.296 | 0.082 | -0.579 | 0.245 |
| KY6Y_L | 113 | 94 | -0.90 | 36 | -13.50 | 0.524 | 0.127 | -0.729 | 0.213 |
| YG1J_R | 138 | 98 | -0.90 | 30 | -16.90 | 0.529 | 0.014 | -0.908 | 0.033 |
| YG3J_R | 148 | 113 | -0.90 | 35 | -12.50 | 0.658 | 0.022 | -0.938 | 0.022 |
| YG3J_L | 82 | 68 | -1.05 | 34 | -1.70 | 0.612 | 0.154 | -0.559 | 0.209 |
| YG4J_R | 265 | 227 | -0.65 | 44 | -32.20 | 0.285 | 0.062 | -0.477 | 0.171 |
| YG4J_L | 164 | 148 | -0.65 | 46 | -31.70 | 0.271 | 0.053 | -0.573 | 0.142 |
| YG5G_R | 158 | 123 | -0.85 | 32 | -17.30 | 0.358 | 0.086 | -0.482 | 0.188 |
| YG5G_L | 125 | 94 | -0.85 | 34 | -15.80 | 0.377 | 0.093 | -0.489 | 0.196 |
| YG5J_L | 113 | 87 | -1.05 | 31 | 1.20 | 0.851 | 0.141 | -0.810 | 0.142 |
| YG7G_L | 78 | 46 | -1.65 | 31 | 13.20 | 1.391 | 0.163 | -0.906 | 0.106 |
| YG9G_R | 152 | 124 | -0.70 | 32 | -27.10 | 0.276 | 0.063 | -0.561 | 0.177 |
| YG9J_L | 165 | 147 | -0.60 | 33 | -27.30 | 0.236 | 0.068 | -0.384 | 0.238 |
| 注:nllh为估计模型的负对数似然度;SE为参数估计值的标准差;*为部分车辆变道时周边没有其他车辆,因此PET个数少于车道变换次数。 | |||||||||
4 极值统计模型的应用 4.1 事故重现水平的提出
根据估计得出的模型参数和式(5),可以计算得到重现水平。在交通安全分析的背景下,考虑到PET值的大小代表的是车道变换过程中发生交通事故的可能程度,并且PET < 0即意味着交通事故的发生,因此将基于PET分布得到的重现水平引申为事故重现水平。结合上文的分析,以NPET为基础数据计算得到的事故重现水平,如果其大于或等于0,则表明重现期内预期有交通事故发生;如果其小于0,则表明重现期内没有交通事故发生。
由于以时间为度量的事故重现水平并不能很好地反映交通量、车道变换次数等基本信息。借鉴百万车事故率的概念,考虑到本文分析的是与车道变换行为相关的交通事故,提出百万次车辆变道事故
重现水平指标,其计算公式如下:
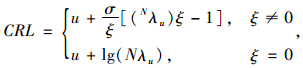
|
(7) |
式中,CRL为百万次车辆变道事故重现水平;u,σ,ξ和λu的意义同式(5);N=106,代表一百万次车道变换行为。百万次车辆变道事故重现水平可以理解为高速公路某一基本路段上每发生一百万次车道变换行为时会出现一次车道变换行为对应的最大NPET大于CRL的情况,或者该路段每一次车道变换行为所对应的NPET大于CRL的概率为百万分之一。如果CRL≥0,则表明每百万次车道变换行为中会产生交通事故;如果CRL < 0,则表明在一百万次车道变换行为中无交通事故发生。
4.2 事故重现水平与交通事故的关系分析事故重现水平和传统的事故率指标相比,其最大的优势在于该指标的计算过程不依赖于历史事故数据。按照式(7)计算得出的各个路段的百万次车辆变道事故重现水平如表 2所示,其与各路段事故次数之间的Pearson相关性系数达到了0.77并且p值为1.27×10-6,这说明二者之间存在显著的强线性正相关关系。相比较于前文得到的车道变换冲突与事故次数之间0.24的相关性水平,通过对PET数据信息进一步挖掘得到的百万次车辆变道事故重现水平与事故次数之间具有更高的相关性。
| 路段编号 | 事故次数/次 | CRL |
| JZ3G_L | 5 | 0.128 |
| JZ4B_R | 1 | -0.272 |
| JZ4G_L | 2 | -0.212 |
| KY1Y_R | 4 | 0.006 |
| KY1Y_L | 3 | 0.037 |
| KY2K_R | 2 | -0.160 |
| KY2K_L | 1 | -0.230 |
| KY2Y_R | 2 | -0.169 |
| KY2Y_L | 1 | -0.239 |
| KY3K_R | 0 | -0.177 |
| KY3K_L | 1 | -0.176 |
| KY3Y_R | 2 | -0.166 |
| KY4K_L | 4 | 0.014 |
| KY5K_R | 0 | -0.121 |
| KY6K_R | 1 | -0.231 |
| KY6K_L | 0 | -0.231 |
| KY6Y_R | 0 | -0.139 |
| KY6Y_L | 1 | -0.181 |
| YG1J_R | 0 | -0.317 |
| YG3J_R | 0 | -0.199 |
| YG3J_L | 5 | 0.044 |
| YG4J_R | 3 | -0.054 |
| YG4J_L | 1 | -0.177 |
| YG5G_R | 0 | -0.109 |
| YG5G_L | 0 | -0.081 |
| YG5J_L | 3 | 0.001 |
| YG7G_L | 1 | -0.115 |
| YG9G_R | 0 | -0.209 |
| YG9J_L | 2 | 0.009 |
| 相关性系数 | 0.77(p=1.27×10-6) | |
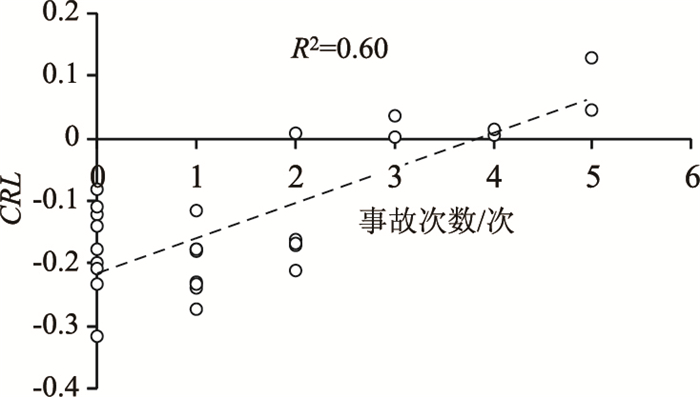
进一步分析百万次车辆变道事故重现水平与事故次数的关系,如图 4所示,也可以发现百万次车辆变道事故重现水平与事故次数之间呈较为明显的正相关关系,并且采用线性趋势线拟合时的决定性系数R2=0.60。这说明百万次车辆变道事故重现水平越高,事故次数就越高,路段也就越危险。因此,作为路段安全性评价指标,百万次车辆变道事故重现水平与历史事故数据具有近似相等的效果,且明显优于交通冲突数指标。
|
| 图 4 事故次数与百万次车辆变道事故重现水平的关系 Fig. 4 Number of accidents vs. accident recurrence level of one million vehicle lane changing maneuvers |
| |
5 结论
本文提出了一种基于非交通事故数据的道路交通安全分析的方法。该方法以车道变换过程中的PET为基础,针对简单界定临界值后所得到的冲突次数与事故次数之间相关性较低的问题,借助于极值理论进行了PET数据的建模和分析,其核心是构建了百万次车辆变道事故重现水平指标,进而对该指标的有效性进行了重点研究。结合实测数据分析,发现百万次车辆变道事故重现水平与交通事故之间具有较好的相关性,说明了该指标可以作为交通安全分析的有效指标,从而为交通安全分析提供了新的工具。本研究的创新之处在于:
(1) 提出了一个完全不依赖于历史事故数据的交通安全分析指标。由于交通事故发生的随机性和稀少性以及事故记录的不完备性,以交通事故数据为基础的安全分析总是受到事故样本量较小的制约。本文所提出的百万次车辆变道事故重现水平指标完全不依赖于交通事故数据,而是以较短时间段内观测得到的大量PET数据为基础,这在一定程度上提高了安全分析的时效性。
(2) 从侧面进一步验证了交通冲突技术的有效性。因为无法保证交通冲突与交通事故之间稳定的关系,交通冲突技术至提出之初就受到诸多质疑。本文利用极值统计方法对常用的交通冲突衡量指标PET的信息进行进一步挖掘,证明了百万次车辆变道事故重现水平与交通事故次数之间有较强的相关性,相当于从侧面验证了交通冲突技术的有效性。
本文主要分析了车道变换过程中的PET,下一步将考虑高速公路基本路段上所有可能的车辆行驶形式(如跟驰行驶过程中的PET等),从而使构建的事故重现水平指标能够全面地反映所研究对象的整体安全状况。同时,本文PET数据的采集时间相对较短,这也可能是影响事故重现水平与事故数相关性的原因之一,下一步将通过收集更长时段的数据来进一步验证所提出指标的有效性。此外,在应用极值理论的过程中,本文所选用的阈值确定方法在阈值确定过程中存在着一定的主观性和不确定性,亟需探寻更为客观的方法来确定阈值,从而提高模型参数估计的精度也是未来研究的重要方向。
| [1] | GUO F, WOTRING B M, ANTIN J F. Evaluation of Lane Change Collision Avoidance Systems Using the National Advanced Driving Simulator, DOT HS 811332[R]. Washington, D.C.:National Highway Traffic Safety Administration, 2010. |
| [2] | 徐慧智, 裴玉龙, 程国柱. 基于期望运行轨迹的车道变换行为安全性分析[J]. 中国安全科学学报 , 2010, 23 (1) : 90-95 XU Hui-zhi, PEI Yu-long, CHENG Guo-zhu. Study on the Safety of Lane-changing Based on Virtual Desire Trajectory[J]. China Safety Science Journal , 2010, 23 (1) : 90-95 |
| [3] | 孟祥海, 郑来, 毕海峰, 等. 高速公路半幅封闭施工区交通特性与交通冲突特性研究[J]. 中国公路学报 , 2013, 26 (2) : 140-146 MENG Xiang-hai, ZHENG Lai, BI Hai-feng, et al. Research on Traffic Characteristics and Traffic Conflicts of One-way Closed Work Zone on Expressway[J]. China Journal of Highway and Transport , 2013, 26 (2) : 140-146 |
| [4] | 周伟, 罗石贵. 路段交通事故多发点的冲突判定方法[J]. 中国公路学报 , 2000, 13 (1) : 84-89 ZHOU Wei, LUO Shi-gui. Traffic Conflict Identification of Road Accident Blackspots[J]. China Journal of Highway and Transport , 2000, 13 (1) : 84-89 |
| [5] | 刘小明, 段海林. 平面交叉口交通冲突技术标准化研究[J]. 公路交通科技 , 1997, 14 (3) : 43-50 LIU Xiao-ming, DUAN Hai-lin. Research on Standard Program of Traffic Conflict Techniques at Intersections[J]. Journal of Highway and Transportation Research and Development , 1997, 14 (3) : 43-50 |
| [6] | 王学明, 姜华平, 吴伟阳. 基于交通冲突技术的非机动车交通安全研究[J]. 公路交通科技 , 2011, 28 (S1) : 110-114 WANG Xue-ming, JIANG Hua-ping, WU Wei-yang. Traffic Safety of Non-motorized Vehicle Based on Traffic Conflict Technique[J]. Journal of Highway and Transportation Research and Development , 2011, 28 (S1) : 110-114 |
| [7] | COOPER P J. Experience with Traffic Conflicts in Canada with Emphasis on Post Encroachment Time Techniques[C]//Proceedings of the NATO Advanced Research Workshop on International Calibration Study of Traffic Conflict Techniques. Copenhage:Springer-Verlag, 1984:75-96. |
| [8] | GETTMAN D, PU L L, SAYED T, et al. Surrogate Safety Assessment Model and Validation:Final report, FHWA-HRT-08-051[R]. Washington, D.C.:Federal Highway Administration, 2008. |
| [9] | HORST A R A, GOEDE M, HAIR-BUIJSSEN S, et al. Traffic Conflicts on Bicycle Paths:A Systematic Observation of Behaviour from Video[J]. Accident Analysis and Prevention , 2014, 62 (18) : 358-368 |
| [10] | PEESAPATI L N, HUNTER M P, RODGERS M O. Evaluation of Post Encroachment Time as a Surrogate for Opposing Left-turn Crashes[C]//The 92nd Annual Meeting of TRB. Washington, D.C.:TRB, 2013. |
| [11] | CAMPBELL K, JOKSCH H C, GREEN P E. A Bridging Analysis for Estimating the Benefits of Active Safety Technologies, UMTRI-96-18[R].Arm Arbor, MI:University of Michigan, 1996. |
| [12] | SONGCHITRUKSA P, TARKO A P. The Extreme Value Theory Approach to Safety Estimation[J]. Accident Analysis and Prevention , 2006, 38 (4) : 811-822 |
| [13] | TARKO A P. Use of Crash Surrogates and Exceedance Statistics to Estimate Road Safety[J]. Accident Analysis and Prevention , 2012, 45 (3) : 230-240 |
| [14] | COLES S. An Introduction to Statistical Modeling of Extreme Values[M]. London: Springer-Verlag, 2001 . |
| [15] | JARUŠKOVÁ D, HANEK M, JARUŠKOVÁ D, et al. Peaks over Threshold Method in Comparison with Block-maxima Method for Estimating High Return Levels of Several Northern Moravia Precipitation and Discharges Series[J]. Journal of Hydrology and Hydromechanics , 2006, 54 (4) : 309-319 |
| [16] | PICKANDS J. Statistical Inference using Extreme Order Statistics[J]. Annals of Statistics , 1975, 3 (1) : 119-131 |
| [17] | GILLELAND E, KA TZ, R W. New Software to Analyze How Extremes Change Over Time[J]. Eos, Transactions American Geophysical Union , 2011, 92 (2) : 13-14 |
 2016, Vol. 33
2016, Vol. 33
