扩展功能
文章信息
- 朱璨, 马如进, 陈艾荣
- ZHU Can, MA Ru-jin, CHEN Ai-rong
- 爆炸荷载作用下缆索承重桥梁塔梁构件的破坏特征
- Damage Characteristics of Steel Girder and RC Pylon of Cable-supported Bridge Suffered from Blast Loading
- 公路交通科技, 2016, 33(8): 92-98
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(8): 92-98
- 10.3969/j.issn.1002-0268.2016.08.014
-
文章历史
- 收稿日期: 2015-08-28
随着全国基础设施建设的快速发展,以斜拉桥和悬索桥为代表的大跨径缆索承重桥梁得以不断的修建,并已成为现代综合交通运输网络中的重要组成部分,对区域和社会经济发展产生深刻而广泛的影响。
作为交通生命线的枢纽工程,大跨径缆索承重桥梁一旦遭受破坏, 将会导致巨大的经济损失,且灾后修复极其困难。目前,国际和国内的暴恐活动已经引起了有关部门的重视。同时,大量危险品、易燃易爆物品运输车辆也对桥梁结构产生较大潜在威胁。对重点的缆索承重桥梁而言,开展相关研究十分必要。
国外方面,自2005年开始重视研究爆炸对桥梁结构的冲击作用及防恐抗爆。Mahoney(2007)[1]依据TM5-1300手册计算爆炸荷载,并将其等效为静力荷载,通过数值模拟研究了预应力混凝土梁桥、钢板梁桥以及上承式悬臂桁架桥在各种爆炸工况下的破坏情况。Suthar(2007)[2]将爆炸荷载等效为静力荷载,采用有限元软件SAP2000研究了恒载、活载和爆炸荷载组合作用下悬索桥的破坏效应。美国烟酒火器与爆炸物品管理局(ATF)根据能够携带炸药的空间估算不同的车型能够携带的简易炸药的等效TNT当量,并认为60%的爆炸恐怖袭击事件都是不大于227 kg的TNT爆炸。一般认为简易炸药一次性爆炸释放能量最高约为4 000磅(1 814 kg)TNT[3]。这样的当量与美国本土遭受的最大汽车炸弹爆炸事故是相当的。
国内方面,近年来也开始关注桥梁结构的抗爆研究,但相关成果很少。刘山洪等(2005)[4]综述了桥梁结构爆炸荷载的特点,指出爆炸荷载作用下公路桥梁以局部破坏形式为主。邓荣兵等(2008)[5]应用ANSYS/LS-DYNA3D软件对桥面接触爆炸冲击波作用下独塔双索面连续钢桁梁斜拉桥的损伤进行了三维数值模拟,结果表明:爆炸冲击波对桥梁的损伤效应呈局部破坏特征,且以破口形式存在。蒋志刚等[6-7]重点研究了桥梁上方导弹袭击时大跨度桥梁的破坏特征。姚树建等[8]重点研究了爆炸物在箱梁内部爆炸造成的局部破坏。
目前,大跨径缆索支撑桥梁对于大跨径缆索承重桥梁爆炸冲击作用研究很少。爆炸研究主要集中于复杂的数值模拟,鲜有利用数值模拟计算结果提出简便公式来满足初步设计的需求。因此本文借鉴现有的爆炸冲击响应研究成果,运用基于CONWEP计算结构在爆炸荷载作用下动力响应的数值仿真手段,开展正交异性钢桥面板、钢筋混凝土桥塔的恐怖爆炸破坏机理研究,重点研究其爆炸荷载模型和爆炸冲击荷载作用下的塑性变形、开裂及破口,得到了变形模式、破口形式等,同时提出适用于大跨径缆索承重桥梁抗爆设计的简化方法与指标。
1 桥梁构件有限元模型 1.1 爆炸物的模拟运用LS-DYNA中的CONWEP编码对桥梁桥面以及栏杆施加荷载。CONWEP编码基于美国军方根据自由空气场爆炸以及地面爆炸炸药产生的冲击波荷载在平板上分布的特点编制,能够根据平板上节点与爆炸点的距离以及两点连成的直线与平板的角度计算荷载。
1.2 材料模型爆炸冲击荷载作用下的结构能够表现出比静荷载作用下的结构更强的性能。这种性能的增加主要来源于高应变率下结构的材料表现出来的性能强化。混凝土和钢材在高应变率下材料的屈服强度、破坏极限强度都会有所提高,这种性能的提高已经被很多试验数据证实。以混凝土为例,素混凝土在加载速率超过10-5s-1后强度有比较大的提高,当应变速率到达10 s-1后,平均抗压强度提高50%~80%。在爆炸荷载作用下混凝土结构应变速率可达到102 s-1以上[9]。
混凝土材料采用LS-DYNA中的MAT_CONCRETE_DAMAGE_RE13(MAT72),即K & C混凝土模型,该模型考虑了混凝土应变率效应[10]。该模型具有自动生成模型参数的能力,在输入所选用混凝土材料轴心抗压强度、密度、泊松比等简单参数后,程序就会自动生成混凝土材料所需要的其余参数及状态方程。C50混凝土材料参数见表 1。在数值模拟计算过程中通过*MAT_ADD_EROSION命令定义混凝土的材料失效准则,通过计算并依据最大失效主应变作为侵蚀准则,当单元主应变大于准则时,即删除相应单元。
| ρ/(kg·m-3) | E/GPa | v | fck/MPa | ftk/MPa |
| 2 650 | 30 | 0.19 | 32.4 | 2.65 |
钢筋单元、钢桥面板的Q345钢材均采用*MAT_PLASTIC_KINEMATIC(MAT3),即塑性双线性随动强化模型,通过失效应变准则来模拟材料破坏[11]。钢材材料参数见表 2。
| 材料 | ρ/(kg·m-3) | E/GPa | v | σs/MPa | Et/GPa | Fs |
| 钢筋 | 7 850 | 207 | 0.3 | 280 | 1.0 | 0.2 |
| Q345 | 7 850 | 207 | 0.3 | 310 | 1.0 | 0.23 |
| Q370 | 7 850 | 207 | 0.3 | 330 | 1.0 | 0.23 |
| Q420 | 7 850 | 207 | 0.3 | 390 | 1.0 | 0.23 |
1.3 基本假定
由于爆炸分析的复杂性与特殊性以及爆炸作用的瞬时性,分析过程中建立局部构件细化有限元模型,恒载作用为主要内力条件,并在模型建立过程中考虑以下几种基本假定:
(1) 不考虑钢筋和混凝土材料之间的黏结和滑移,采用分离式共节点模型模拟混凝土桥塔;
(2) 钢箱梁塔模型中,所用焊缝均视为刚接;
(3) 钢箱梁局部节段模型考虑箱梁的初始轴力。
1.4 构件有限元模型数值计算中考虑两种典型的缆索承重桥梁的构件,即钢箱梁、钢筋混凝土桥塔,分别建立有限元分析模型。
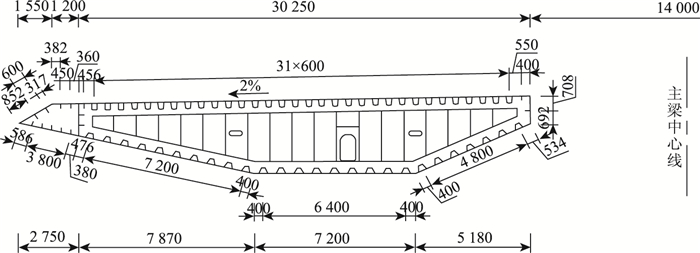
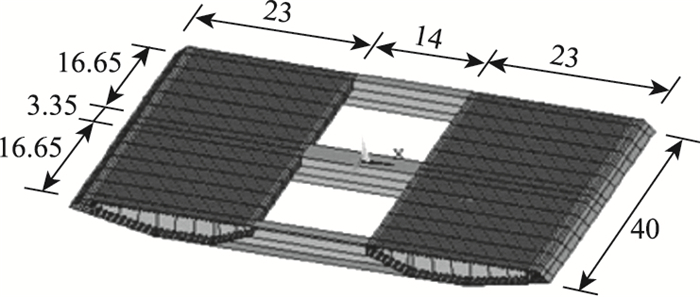
局部节段钢箱梁模型依据分离式钢箱梁,其总长度为43.2 m,钢主梁横隔板间距为3.33 m,如图 1钢箱梁节段尺寸所示。但有限元模型划分单元网格时,钢主梁桥面板网格尺寸边长控制在20 cm以内。钢主梁的约束条件:箱梁两端约束板单元所有节点的竖向和横桥向位移,一端约束板单元所有节点的纵桥向位移,另外一端不约束纵桥向位移。钢箱梁局部有限元模型尺寸见图 2。
|
| 图 1 钢箱梁节段尺寸(单位:mm) Fig. 1 Dimensions of steel box girder segment(unit:mm) |
| |
|
| 图 2 钢箱梁节段有限元模型(单位:m) Fig. 2 Finite element model of steel box girder segment(unit:m) |
| |
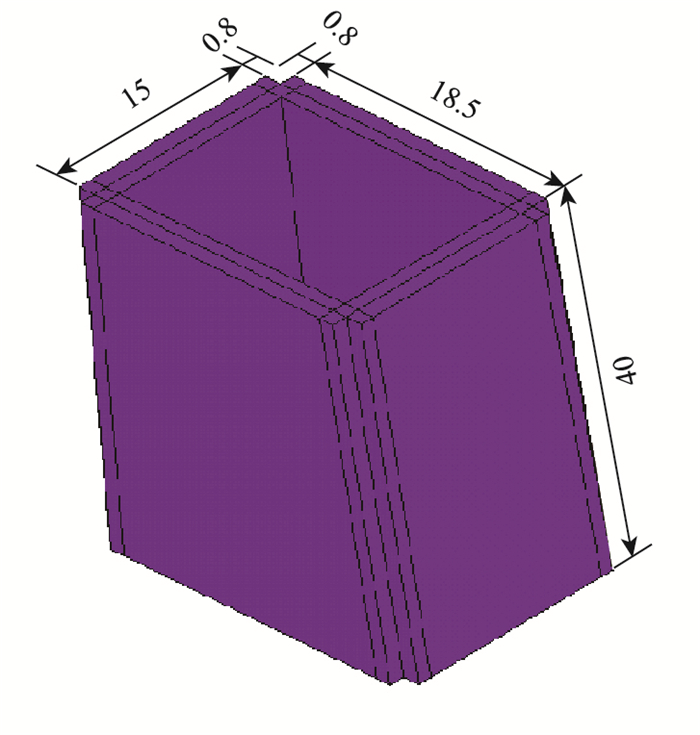
局部节段钢筋混凝土桥塔模型,网格尺寸边长控制在20 cm以内,总高度40 m,桥塔壁厚1.8 m。桥塔实体模型的边界条件:上、下端固结,约束三个方向自由度。模型如图 3所示。
|
| 图 3 钢筋混凝土桥塔节段有限元模型(单位:m) Fig. 3 Finite element model of RC pylon segment(unit:m) |
| |
1.5 爆炸模拟工况
爆炸当量选取与位置不同,对结构损伤会产生明显的差异。本文根据美国烟酒火器与爆炸物品管理局(ATF)的规定,选择3种不同的当量等级,分别为227, 454 kg和1 814 kg TNT。对于钢主梁而言,横隔板的存在会对爆炸的损伤产生明显的差异,因此在分析过程中比较了爆炸位置位于两横隔板中间和位于横隔板正上方这两种情况。针对桥塔则选择接近于桥塔的外侧车道位置。表 3给出了钢主梁的分析工况,表 4给出了混凝土主塔的分析工况。
| 工况 | 1 | 2 | 3 | 4 | 5 | 6 |
| 爆炸位置 | 两横隔板中间, 距顶板1.5 m | 横隔板正上方, 距顶板1.5 m | ||||
| 炸药当量/kg | 227 | 454 | 1 814 | 227 | 454 | 1 814 |
| 工况 | 1 | 2 | 3 |
| 爆炸位置 | 车道上方1.5 m,距离混凝土塔塔壁2.5 m | ||
| 炸药当量/kg | 227 | 454 | 1 814 |
2 构件局部破坏特征 2.1 钢箱梁的局部破坏特征
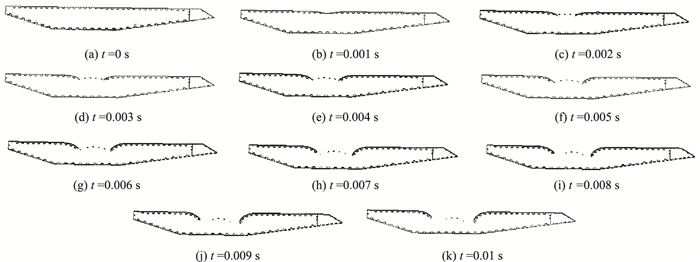
针对钢箱梁的爆炸,分析表明在爆炸冲击波作用下,桥面板顶板迅速产生局部大变形,逐渐开裂形成花瓣状破口和破片。在破口产生后,冲击波进入箱体并在箱内传播,与横隔板、底板产生作用。顶板的破片冲击地板,使其产生局部的塑性变形。瞬时冲击波作用箱梁破坏规律如图 4所示。
|
| 图 4 钢箱梁在冲击波作用下的损伤过程 Fig. 4 Damage process of steel box girder under shock wave action |
| |
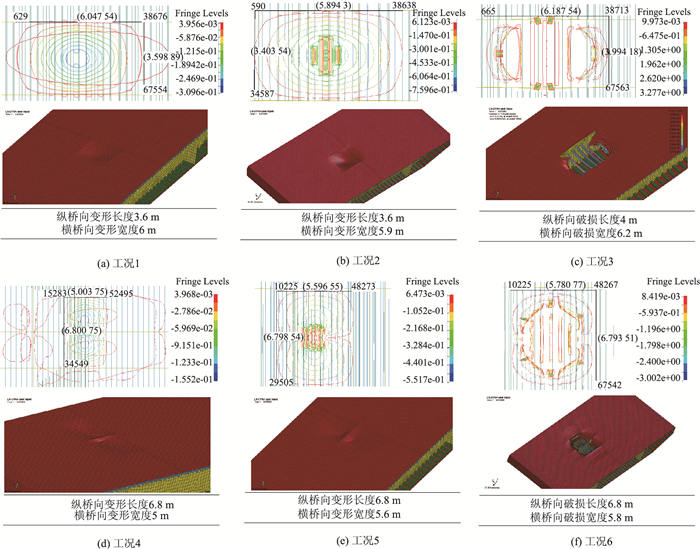
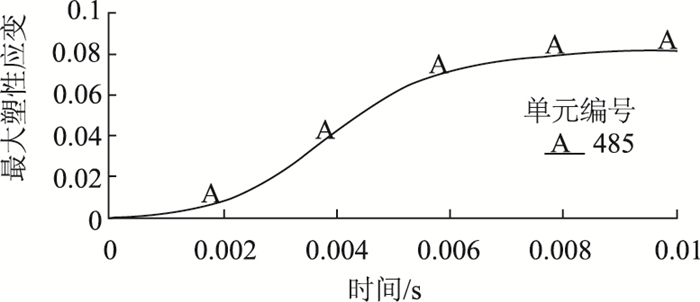
图 5则给出了不同工况下钢箱梁损伤特征与范围。由工况1~3的比较以及4~6的比较可以发现,在不同爆炸等级下,受到影响的箱梁范围基本相近,即爆炸点位于横隔板中间时,影响区域约为4 m×6 m,当爆炸点位于横隔板正上方时,影响区域约为6.8 m×5.6 m。不同爆炸位置的损伤比较可以发现,横隔板的破坏会使得爆炸损伤扩大,由一个箱梁隔室扩展到两个箱梁隔室。可见,爆炸损伤是以隔室为单位向四周扩散。在横隔板损伤条件下,损伤会向临室发展。另外,随着爆炸等级的增加,损伤特征也逐渐由较大塑性变形向破损发展,在227 kg当量下,下陷深度最深达15 cm,两根U肋断裂;在454 kg当量下,下陷最大深度为55 cm,部分材料破损,4根U肋断裂;在1 814 kg当量下,下陷最大深度为0.6 m,靠近爆炸点位置的8根U肋断裂。当爆炸位置距顶板1.5 m时,爆炸当量为450 kg左右,顶板会出现破裂,相应开裂位置的单元应变时程曲线如图 6所示。
|
| 图 5 钢主梁破坏结果(单位:m) Fig. 5 Damage result of steel box girder(unit:m) |
| |
|
| 图 6 454 kg TNT爆炸开裂位置应变曲线 Fig. 6 Strain curve of cracking position under blast of 454 kg TNT |
| |
根据上述分析结果,可以提取出钢箱梁局部破坏指标,并总结如下:
(1) 破损长度一般为2×L,其中L为横隔板间距。
(2) 经过计算主梁的多种爆炸当量和爆炸位置的破损宽度均小于7 m,可见对于车辆爆炸破损宽度约为7 m。
(3) 在模型中的爆炸破损近似于圆形或椭圆形。
(4) 破损估算面积为(2×L×7)m2。
2.2 混凝土桥塔的局部破坏不同爆炸当量的混凝土桥塔爆炸在爆炸作用下的位移结果如图 7所示,可见随着爆炸等级的提高,桥塔位移越大,桥塔受影响范围也越大。227 kg和454 kg爆炸对混凝土桥塔的影响非常小,没有出现明显的受损现象,1 814 kg TNT爆炸后桥塔出现大约5 m×4 m的损伤区域。

|
| 图 7 不同当量混凝土桥塔爆炸结果 Fig. 7 Damage result of RC pylon |
| |
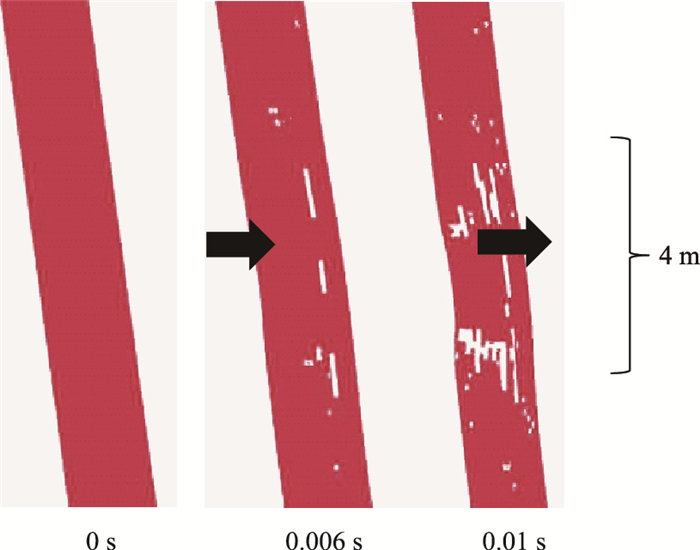
针对1 814 kg的爆炸,本文给出了塔壁的损伤过程如图 8所示,爆炸发生后在塔壁背面首先出现混凝土损伤,然后损伤朝向爆炸方向逐渐发展,最终成型。塔壁损伤以局部破损和层状劈裂为主,塔壁出现明显的内凹变形,但没有出现前后贯穿的破坏,同时混凝土桥塔的塔壁较厚刚度较大,爆炸后的桥塔受损不会导致结构体系崩溃,但是破损面积大、损伤程度复杂必然会导致桥塔的安全性能的下降。
|
| 图 8 1 814 kg TNT爆炸桥塔损伤发展过程 Fig. 8 Damage process of RC pylon under 1 814 kg TNT explosion |
| |
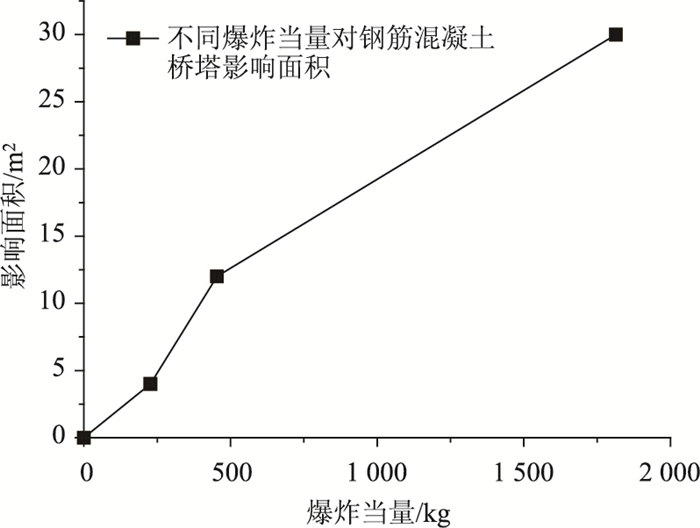
227, 454 kg和1 814 kg TNT当量爆炸对于钢筋混凝土桥塔的影响范围见表 5,从中可以看出,随着爆炸当量的增加,桥塔受影响面积增大, 从图 9中可以看出爆炸影响面积与爆炸当量之间是近似于线性的关系。
| 爆炸当量/kg | 227 | 454 | 1 814 |
| 影响范围/m2 | 2×2 | 3×4 | 6×5 |
|
| 图 9 三种当量爆炸对钢筋混凝土桥塔影响面积 Fig. 9 Effect area of RC pylon under 3 typical explosion equivalents |
| |
桥塔的损伤要比钢箱梁桥面损伤轻很多,这是由于栏杆与桥塔尚有较远的距离,桥塔的壁厚为1.8 m也远厚于桥面的顶板厚度。
为减轻混凝土主塔在汽车炸弹桥面爆炸冲击作用下的破坏程度,保证其剩余承载力,应提高主塔壁的塑性变形能力,耗散较多的爆炸冲击能量。为减小主塔壁破口范围,可适当加密相应位置的横纵向箍筋,发挥箍筋对破口的约束作用。
2.3 爆炸作用简化计算方法前文中对爆炸作用的影响均采用的是conwep算法,需要建立板单元模型和实体单元模型,过程较为复杂,无法利用常用的梁单元进行模拟,实用性较低。因此,通过计算结果提取出规律公式,以满足工程应用的需求。规律公式主要涵盖了极端状况下的静力计算和极端状况下的动力计算。
2.3.1 极端状况静力计算:不同爆炸当量会对钢桥面板的损伤面积不同,通过计算多种爆炸工况,爆炸当量从10 kg到1 814 kg不等,可以从结果中提取出钢箱梁局部破坏简化计算方法,并总结如下:
(1) 当爆炸当量不小于200 kg时,计算破损长度为2×L,计算破损宽度为7 m,其中L为横隔板间距,破损计算面积为(2×L×7)m2;
(2) 当爆炸当量小于200 kg时,计算破损长度和计算破损宽度线性内插,破损计算面积按照矩形计算;
(3) 认为破损面积内的钢箱梁顶板在爆炸中消失,钢箱梁变为开口截面,重新计算截面特性。
爆炸对于钢筋混凝土桥塔的影响较小,可能发生的一般当量的爆炸造成钢筋混凝土桥塔受损的可能性较小,因此可以认为钢筋混凝土桥塔在爆炸中不会受损。
爆炸发生时,由于结构振动和爆炸荷载冲击,恒、活载会出现一定程度的增大,参考国外的相关规范[12],认为在爆炸发生位置纵桥向50 m范围内,恒、活载会增大,恒、活载增大系数为2。
将爆炸峰值压力P0(建议值为3.5×109×exp[(1-|X|)/2.2]N,|X|为计算点距离起爆中心距离)以集中力的形式施加在梁系有限元模型上。
2.3.2 极端状况动力计算:建立梁系有限元模型,将爆炸时程作用力以集中力的方式加载在模型上,计算模型的动力响应。
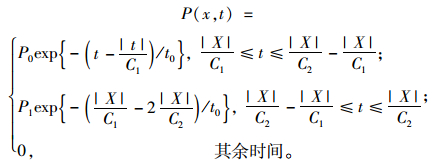
|
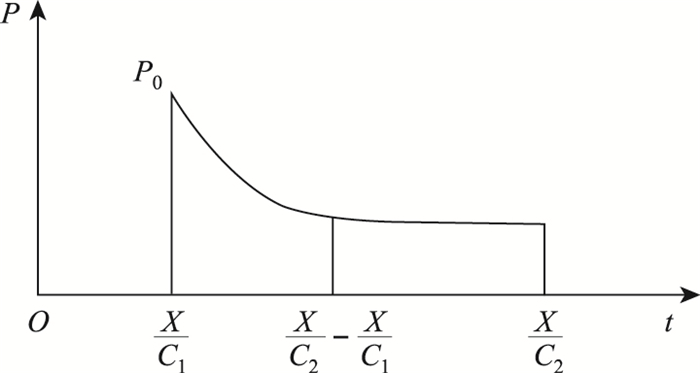
式中,P0为爆炸过程中的峰值压力(建议值3.5×109×exp[(1-|X|)/2.2]N; C1为冲击波的传递速度(建议值1 800 m/s); C2为热空气的传播速度(建议值800 m/s);t0为时间常数(建议值0.01 s); |X|为计算点距离起爆中心距离; t为时间。
|
| 图 10 压力时程曲线 Fig. 10 Curve of pressure vs. time history |
| |
3 结论与展望
本文针对缆索承重桥梁的钢箱梁与混凝土桥塔在爆炸荷载作用下的损伤特征进行了分析,得到结论如下:
(1) 针对钢箱梁,比较了多种当量和爆炸位置,发现加劲肋对于限制破口面积发挥巨大的作用;
(2) 对于钢箱梁,按照不同当量不同位置的计算结果,提出了多项局部破坏指标,便于钢箱梁抗爆设计;
(3) 针对钢筋混凝土主塔,比较了多种当量,发现混凝土桥塔对于爆炸的抵抗能力较强。
由于问题本身的复杂性以及作者时间和水平的限制,还有许多工作有待进一步研究:
(1) 只进行了钢筋混凝土桥塔的抗爆性能的分析,对于钢主塔的抗爆性能未进行研究;
(2) 文章中采用*LOAD_BLAST命令,与流固耦合的方法之间的差异有待进一步比较;
(3) 需要展开爆炸作用下桥梁结构可靠度研究。
| [1] | MAHONEY E E. Analyzing the Effects of Blast Loads on Bridges Using Probability, Structural Analysis and Performance Criteria[D]. College Park:The University of Maryland, 2007. http://www.researchgate.net/publication/277159668_Analyzing_the_effects_of_blast_loads_on_bridges_using_probability_structural_analysis_and_performance_criteria |
| [2] | KUNAL S. The Effect of Dead, Live and Blast Loads on A Suspension Bridge[D]. College Park:The University of Maryland, 2007. http://drum.lib.umd.edu/bitstream/handle/1903/7181/umi-umd-4564.pdf;sequence=1 |
| [3] | MARCHAND K A, WILLIAMSON A E B, WINGET D G. Analysis and Design of Critical Bridges Subjected to Blast Loads[J]. Journal of Structural Engineering , 2005, 131 (8) : 1243-1255 |
| [4] | 刘山洪, 魏建东, 钱永久. 桥梁结构爆炸分析特点综述[J]. 重庆交通学院学报 , 2005, 24 (3) : 16-17 LIU Shan-hong, WEI Jian-dong, QIAN Yong-jiu. State-of-the-art of Research and Analysis of Structure and Bridge under Blast Loads[J]. Journal of Chongqing Jiaotong University , 2005, 24 (3) : 16-17 |
| [5] | 邓荣兵, 金先龙, 陈向东, 等. 爆炸冲击波作用下桥梁损伤效应的数值仿真[J]. 上海交通大学学报 , 2008, 42 (11) : 1927-1930 DENG Rong-bing, JIN Xian-long, CHEN Xian-dong, et al. Numerical Simulation for the Damage Effect of Bridge Subjected to Blast Wave[J]. Journal of Shanghai Jiaotong University , 2008, 42 (11) : 1927-1930 |
| [6] | 蒋志刚, 王赟, 严波, 等. 爆炸荷载作用下悬索桥竖弯响应的数值模拟[J]. 振动与冲击 , 2012, 31 (2) : 123-128 JIANG Zhi-gang, WANG Yun, YAN Bo, et al. Numerical Simulation for Vertical Bending Response of a Suspension Bridge under Air Explosion Loading[J]. Journal of Vibration and shock , 2012, 31 (2) : 123-128 |
| [7] | 蒋志刚, 白志海, 严波, 等. 钢箱梁桥面板爆炸冲击响应数值模拟研究[J]. 振动与冲击 , 2012, 31 (5) : 77-81 JIANG Zhi-gang, BAI Zhi-hai, YAN Bo, et al. Numerical Simulation for Response of a Steel Box Girder Deck to Blast Loading[J]. Journal of Vibration and shock , 2012, 31 (5) : 77-81 |
| [8] | 姚本健, 蒋志刚, 卢芳云, 等. 汽车炸弹钢箱梁内部爆炸局部破坏效应分析[J]. 振动与冲击 , 2015, 34 (7) : 222-227 YAO Ben-jian, JIANG Zhi-gang, LU Fang-yun, et al. Analysis on Local Damage of Steel Box Girder under Internal Blast Loading of Vehicle Bomb[J]. Journal of Vibration and Shock , 2015, 34 (7) : 222-227 |
| [9] | 闫东明. 混凝土动态性能试验研究现状及展望[J]. 水科学与工程技术 , 2006, 7 (4) : 1-6 YAN Dong-ming. Current Situation and Prospect of Concrete Dynamic Performance Test[J]. Water Science and Engineering Technology , 2006, 7 (4) : 1-6 |
| [10] | 匡志平, 袁训康. RHT混凝土本构模型强度参数分析与模拟[J]. 力学季刊 , 2012, 33 (1) : 158-163 KUANG Zhi-ping, YUAN Xun-kang. The Analysis and Simulation for the Strength Parameters of RHT Concrete Model[J]. Chinese Quarterly of Mechanics , 2012, 33 (1) : 158-163 |
| [11] | 张涛, 马如进, 陈艾荣. 爆炸荷载作用下斜拉桥的结构特性[J]. 重庆交通大学学报:自然科学版 , 2013 (S1) : 784-787 ZHANG Tao, MA Ru-Jin, CHEN Ai-rong. Structural Characteristics of Cable-Stayed Bridge under Blast Loads[J]. Journal of Chongqing Jiaotong University:Natural Science Edition , 2013 (S1) : 784-787 |
| [12] | EN 1991-1-7:Eurocode 1:Action on Structures-Part 1-7:General Actions-Accidental Actions[S]. |
 2016, Vol. 33
2016, Vol. 33
