扩展功能
文章信息
- 龚慧星, 刘志文
- GONG Hui-xing, LIU Zhi-wen
- 矩形断面柱体涡激振动数值模拟与机理分析
- Numerical Simulation and Mechanism Analysis of Vortex-induced Vibration of Rectangular Cylinder
- 公路交通科技, 2016, 33(8): 76-85
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(8): 76-85
- 10.3969/j.issn.1002-0268.2016.08.012
-
文章历史
- 收稿日期: 2015-09-28
涡激振动是由于结构尾流区旋涡脱落所引起的一种振动现象,具有强迫、自激、限幅等特点,是一种典型的非线性振动。实际工程结构如桥梁、高层建筑、索、热交换管及钻井平台立管等都有可能发生涡激共振,对结构疲劳性能和使用性能具有重要影响,因此必须予以重视[1]。
结构涡激振动数值模拟主要有二维数值模拟和三维数值模拟。涡激振动二维数值模拟具有网格少、计算效率高等优点,国内外许多学者针对圆柱、方柱以及矩形等钝体断面的涡激振动问题进行了二维数值模拟。Nomura采用基于任意拉格朗日-欧拉法计算了雷诺数分别为Re=100,400时圆柱和H形柱体的涡激振动响应[2-3]。曹丰产等采用动网格方法考虑圆柱体与流体的耦合,采用二阶投影法和多重网格法求解N-S方程,柱体振动方程采用Newmar k-β方法进行求解,实现了圆柱涡激振动响应的数值模拟[4]。徐枫、欧进萍采用动网格技术和滑移网格技术对二维方柱进行非定常绕流与涡激振动数值模拟[5]。Pan等采用k-ω SST湍流模型对二维圆柱进行涡振响应数值模拟。研究表明,二维数值结果不能真实反映漩涡脱落的三维效应[6]。方平治[7]、李永乐[8]均采用松耦合方法对二维方柱的涡振进行了数值模拟。刘志文等采用二维雷诺平均(RANS)k-ω SST湍流模型和动网格技术,对宽高比为4的矩形断面涡激振动响应进行了计算,数值模拟结果与试验结果吻合良好[9]。Al-Jamal H.等采用大涡模拟对雷诺数为Re=8 000时的二维圆柱进行了涡振数值模拟[10]。近年来涡激振动的三维数值模拟逐渐受到关注。Sarwar等采用大涡模拟方法分别对宽高比为4的矩形断面和箱梁断面进行了涡激振动三维数值模拟研究[11]。Zhao等采用PG-FEM求解三维N-S方程,实现弹性支承三维圆柱涡激振动数值模拟,并与二维数值模拟结果进行了比较[12]。
综上所述,结构涡激振动数值模拟目前主要以二维数值模拟为主,涡激振动三维数值模拟及机理研究相对较少。本文采用滑移网格与动网格相结合的方法解决涡激振动数值模拟中可能出现的网格畸变、负体积等问题,并对矩形断面竖向涡激振动机理进行探讨。
1 计算方法 1.1 流体控制方程与并行计算简介二维数值模拟采用雷诺平均(RANS)求解不可压缩N-S方程,在直角坐标系下,基于雷诺平均的连续性方程和N-S方程为:
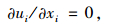
|
(1) |
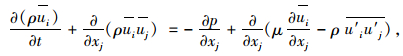
|
(2) |
式中,i, j=1, 2;ρ为空气密度,ρ=1.225 kg/m3;μ为动力黏性系数,μ=1.789×10-5kg/(m·s)。
三维数值模拟采用大涡模拟(Large Eddy Simulation, LES)方法求解不可压缩N-S方程。其基本假设如下:(1) 动量、能量、质量及其他标量主要由大涡输送;(2) 结构的几何外形和边界条件决定了大涡特性,且流动特性主要在大涡中体现;(3) 小尺度漩涡受结构几何外形和边界条件影响较小,并且各向同性,大涡模拟过程中直接求解大涡,利用亚网格尺度模型模拟小尺度紊流运动对大尺度旋涡运动的影响。
LES的控制方程是通过对N-S方程进行空间滤波得到,滤波过程是去掉比过滤尺度小的漩涡,从而得到大涡控制方程:
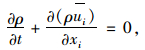
|
(3) |
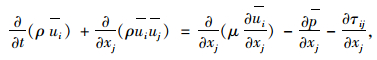
|
(4) |
式中,ρ为空气密度,ρ=1.22 5 kg/m3;ui, uj为速度分量;p为压力;μ为运动黏性系数;τij为亚网格应力,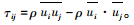
Smagorinsky于1963年提出了亚格子模型,至今仍然被广泛应用,该模型采用涡黏性概念假设,所求解速度场相关联的拉伸张量分量Sij的偏斜部分τija可以表示为:
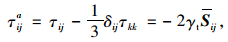
|
(5) |
式中,γt为涡黏性系数;δij为Kroneker符号(当i=j时,δij=1;当i≠j时,δij=0);Sij为滤波后的变形速率张量,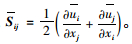
Smagorinsky模型假设γt∝l·qSGS,其中l是未求解涡的混合尺度,qSGS是对应的速度比尺。假设l=Cs·Δ,Δ与普朗特混合长假设相类似,速度比尺qSGS与速度梯度直接相关,即qSGS=|S|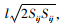
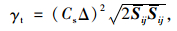
|
(6) |
式中Cs一般取为0.10。
Fluent并行计算就是利用多个计算节点(处理器)同时进行计算。并行计算可将网格分割成多个子域,子域的数量是计算节点的整数倍,每个子域会在不同的计算节点上进行计算,因而可提高计算速度。但是计算信息传输率的增加将导致并行计算效率降低,并非节点数越多计算效率越高,还和网格规模相关,因此进行并行计算时合理选择计算节点数非常重要。矩形断面涡振并行计算在基于Windows Server 2008 R2 Standard操作系统的Sugon W5801-G10型号(32物理核,32 G内存,主频2.0 GHz,2T硬盘)计算机上开展。二维模拟总共10个工况,三维模拟总共11个工况,每个二维工况计算占用6核,每个三维工况占用10核,计算至收敛分别耗时大致2~4 d及5~7 d。
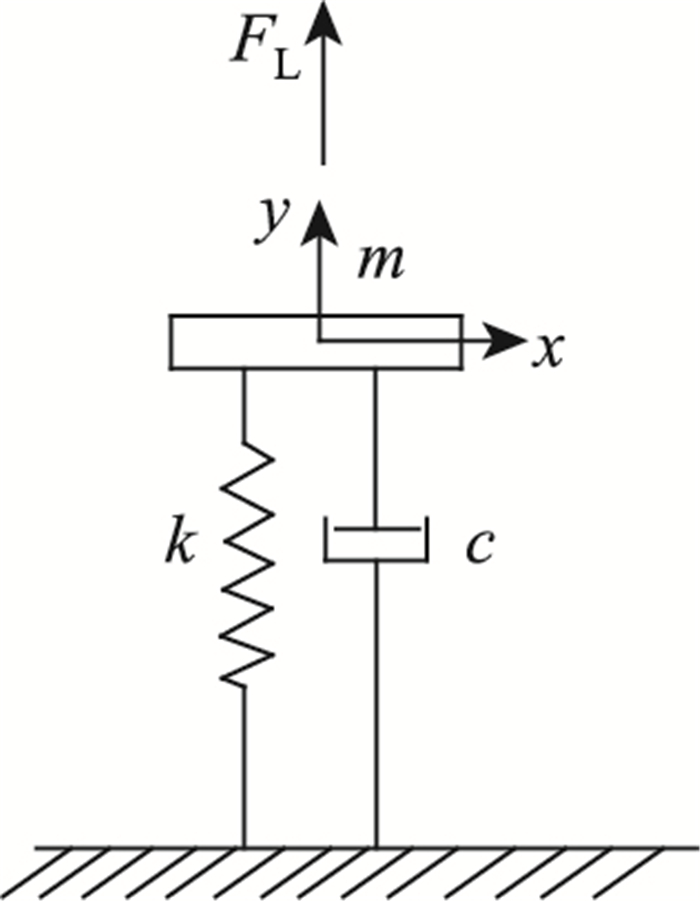
1.2 结构振动控制方程将矩形断面柱体竖向涡振简化为弹性支承单自由度振子模型,如图 1所示。对应的结构振动控制方程为:
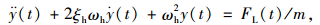
|
(7) |
式中,y(t), ẏ(t), ÿ(t)分别为时刻t对应的结构竖向振动位移、速度和加速度;ξh为弹性支承结构竖向振动系统阻尼比;ωh为弹性支承结构竖向振动系统圆频率;m为单位长度结构质量;FL(t)为时刻t对应的单位长度柱体所受到的升力。
|
| 图 1 结构涡激振动模型 Fig. 1 VIV model of structure |
| |
1.3 计算域、边界条件及网格划分
根据文献[13]确定矩形断面竖向涡激振动数值模拟计算参数,见表 1。
| 参数 | 宽B/mm | 高D/mm | 长L/mm | 单位长度质量/(kg·m-1) | 竖向频率/Hz | 竖向阻尼比/% |
| 数值 | 300 | 60 | 15 | 6.375 | 6.152 | 0.450 |
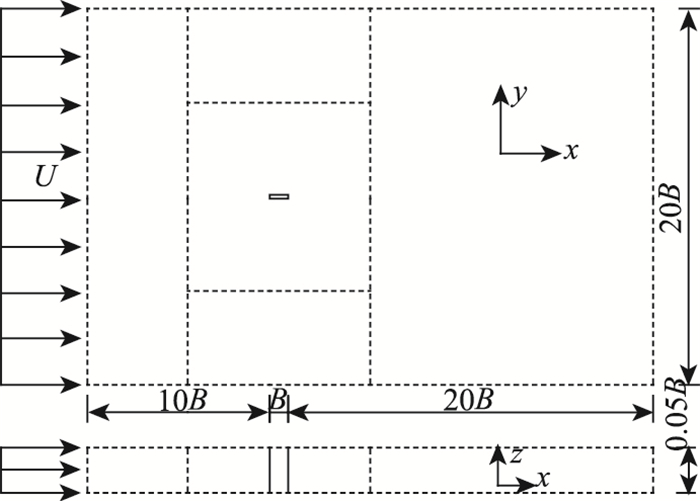
根据经验确定计算域,上、下侧边界距离矩形断面中心为10B;上游边界距离矩形断面中心为10.5B;下游边界距离矩形断面中心为20.5B;三维数值模拟对应的沿矩形断面展向长度为15 mm,模型阻塞率为1.0%。边界条件设置如下:入口边界采用速度入口,攻角为0°,湍流强度设为Iu=0.5%,湍流黏性比为10%;出口边界条件采用压力出口;上、下侧采用滑移壁面边界条件,三维数值模拟对应前后侧采用对称边界条件;矩形断面柱体周围采用无滑移边界条件。三维断面流场几何模型如图 2所示。
|
| 图 2 三维矩形断面柱体流场几何模型 Fig. 2 Geometrical model of flow field of a 3D rectangular cylinder |
| |
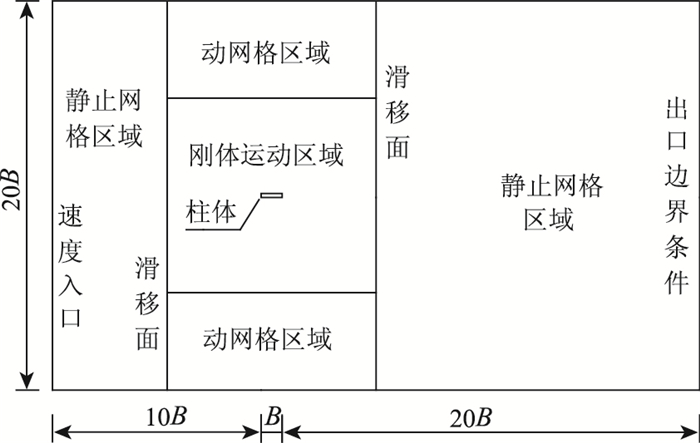
为解决单纯用动网格方法时出现网格畸变、负体积等质量问题,提出采用滑移网格和动网格技术相结合的方法进行结构涡振响应计算。考虑到Fluent在默认情况下弹性光顺法仅适用于三角形网格和四面体网格,本文通过命令(rpsetvar 'dynamesh/spring /all-element-type? #t)实现对结构化四边形和六面体网格进行弹性光顺法动网格更新[14]。在进行网格划分时采用分块划分思路,即采用“刚体运动区域+动网格区域+滑移面+静网格区域”进行网格划分,如图 3所示。靠近结构附近的刚体运动区域随结构一起做竖向振动,动网格区域吸收刚体竖向运动带来的变形,由于该区域距离矩形断面较远,网格间距较大,在较小时间步的条件下采用弹性光顺法网格不会产生负体积。
|
| 图 3 矩形断面网格分块划分及边界条件 Fig. 3 Gridding and boundary conditions of rectangular section |
| |
根据以上网格划分方法,分别建立了矩形断面柱体二维网格和三维网格。二维网格通过静止绕流方法对网格和时间步无关性进行验证,如表 2所示。考虑计算效率与精度,二维网格总数为58 850,时间步长取为0.001 s。三维网格由于是基于二维网格展向拉伸获得,故未进行网格与时间步无关性验证。二维网格模型模型近壁面第一层网格中心至矩形断面表面的距离为δ=0.000 1B,二维网格模型全部采用四边形结构化网格,如图 4所示。
| 网格数 | dT/s | Cd | CLrms | St | 绕流20 s耗时/h |
| 36 000 | 0.001 | 1.1 | 0.16 | 0.117 | 5~6 |
| 84 750 | 0.001 | 1.05 | 0.155 | 0.115 | 23~24 |
| 58 850 | 0.001 | 1.02 | 0.108 | 0.117 | 15~16 |
| 58 850 | 0.000 5 | 1.02 | 0.109 | 0.117 | 26~27 |
| 58 850 | 0.005 | 1.04 | 0.132 | 0.109 | 3~4 |
| 58 850 | 0.01 | 1.06 | 0.17 | 0.088 | 1~2 |

|
| 图 4 矩形断面柱体二维网格划分 Fig. 4 Two-dimensional gridding of rectangular cylinder |
| |
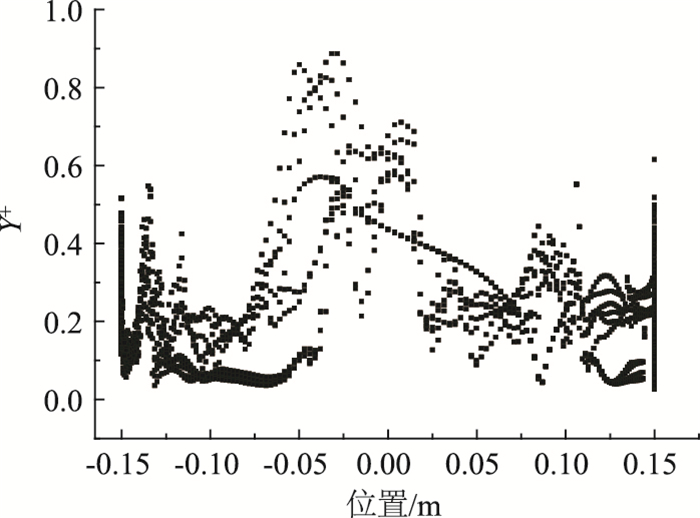
考虑结构涡激振动计算效率,将二维网格模型沿展向拉伸5层建立三维网格模型,展向长度为15 mm,三维网格模型全部采用六面体结构化网格,网格总数为294 250。矩形断面柱体三维网格划分见图 5。静止绕流计算收敛后得到的矩形断面最大Y+值小于1,即满足LES对Y+的要求,如图 6所示。

|
| 图 5 矩形断面柱体三维网格划分 Fig. 5 Three-dimensional gridding of rectangular cylinder |
| |
|
| 图 6 柱体壁面的Y+分布 Fig. 6 Y+ distribution on rectangular cylinder surface |
| |
1.4 求解参数设置
首先对矩形断面柱体涡激振动进行二维雷诺平均(RANS)数值模拟,采用Fluent6.3中k-ω SST湍流模型求解流场,采用SIMPLEC算法求解速度压力耦合方程组;雷诺应力项采用PRESTO!离散格式进行求解;动量及湍流动能项均采用QUICK求解;耗散速率项采用二阶格式求解。为求得柱体涡振响应,先进行静止绕流计算,时间步长取0.001 s,计算残差设置为5×10-4,充分绕流后导入多核并行UDF程序进行流固耦合计算。在每个时间步内获取柱体断面所受到的升力,将升力代入柱体振动方程,采用Newmar k-β法求解柱体振动响应,然后将柱体速度赋予给刚体运动区域并与柱体一起运动,进行网格更新和流场计算,计算完成后进入下一步迭代直至结果收敛。涡振模拟时计算时间步、计算残差与静止绕流时保持一致。大涡模拟在Fluent 6.3程序中求解,采用SIMPLEC算法求解速度压力耦合方程组;压力项采用Standard离散格式求解;动量项采用中心差分格式求解。计算时间步长、计算残差取值及具体计算流程与二维数值模拟相同。
2 计算结果 2.1 柱体静止绕流结果首先对矩形断面柱体分别进行二维、三维绕流计算,矩形断面柱体三分力系数和斯托罗哈数定义如下:
阻力系数:
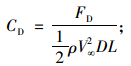
|
(8) |
升力系数:
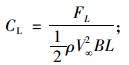
|
(9) |
升力矩系数:
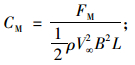
|
(10) |
斯托罗哈数:
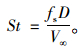
|
(11) |
上述式中:FD,FL及FM分别为作用在矩形断面柱体上的阻力、升力和升力矩;V∞为来流风速;ρ为空气密度;B,D及L分别为矩形断面的宽、高和长,对于二维模型L=1.0 m;fs为旋涡脱落频率。
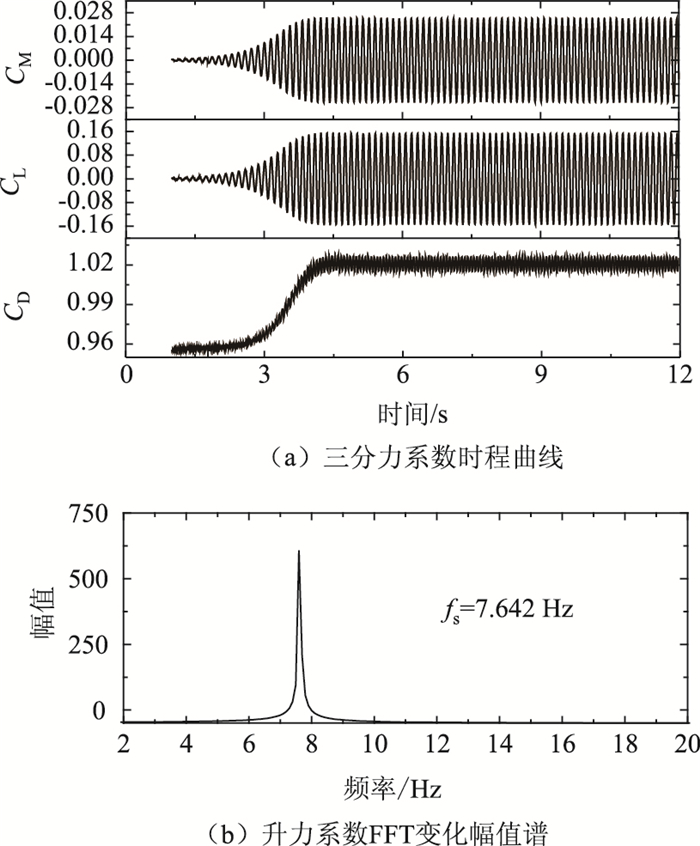
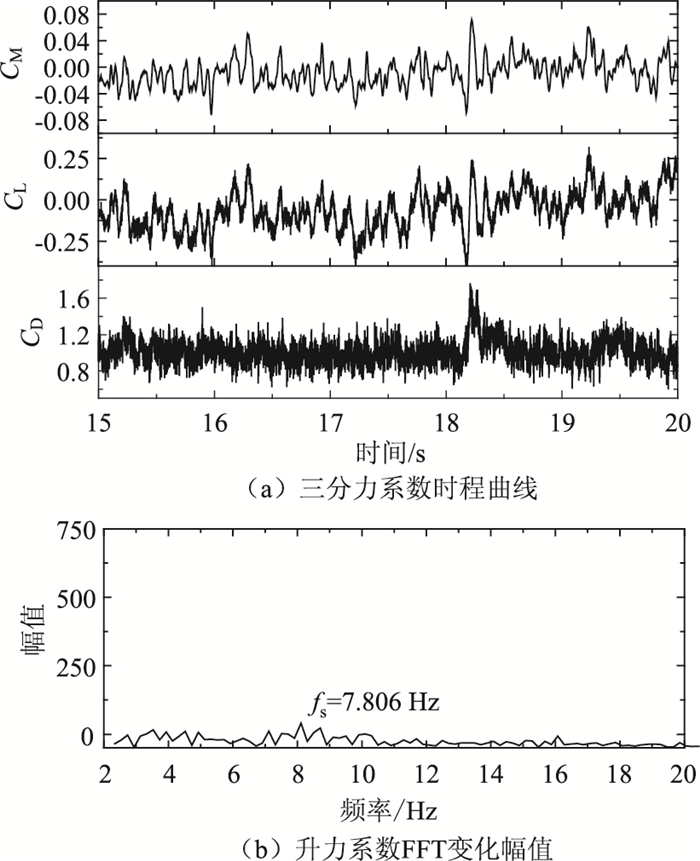
限于篇幅,仅给出风速为V∞=3.89 m/s时矩形断面柱体二维、三维数值模拟结果对应的三分力系数时程曲线及升力系数傅立叶变换频谱图,如图 7、图 8所示。表 3给出了矩形断面阻力系数、升力系数根方差以及斯托罗哈数计算结果。
|
| 图 7 静止矩形断面二维数值模拟结果 Fig. 7 Two-dimensional numerical simulation result of stationary rectangular section |
| |
|
| 图 8 静止矩形断面柱体三维数值模拟结果 Fig. 8 Three-dimensional numerical simulation results of stationary rectangular cylinder |
| |
从图 7、图 8中可以看出,矩形断面涡激振动二维数值模拟结果显示三分力系数围绕其均值振荡,升力系数FFT变换幅值谱显示涡脱频率较单一;三维数值模拟结果显示三分力系数具有一定的随机特性,升力系数FFT变换幅值谱显示涡脱频率成份较多。其主要原因是RANS方法求解平均量方程,将脉动运动全部细节平均,而LES方法直接求解大尺度的涡,过滤后的小尺度涡虽不能产生决定性的影响,但对大尺度涡紊流特性有一定的影响。从表 3中可以看出,矩形断面阻力系数、斯托罗哈数二维数值模拟结果与三维数值模拟结果较接近,且与文献[15-16]均比较接近。矩形断面升力系数根方差二维和三维数值模拟结果均比文献[16]的计算值偏大,相对而言与文献[15]试验结果更为接近。
2.2 柱体竖向涡振数值模拟结果文献[13]中设计并制作了宽高比为5的矩形断面节段模型,在湖南大学HD-2边界层风洞第二试验段进行试验,分别在均匀流场和紊流场中测试了模型表面压力、尾流风速、振动位移等。参考风洞试验数据确定矩形断面二维数值模拟折算风速分别Vred=V∞/fhD=5.95,6.88,7.86,8.70,9.56,10.54,11,11.40,11.81及12.70;矩形断面柱体三维数值模拟折算风速分别为Vred=V∞/fhD=5.95,6.88,7.86,8.13,9.56,10.54,11.05,11.32,11.60,11.81及12.70。
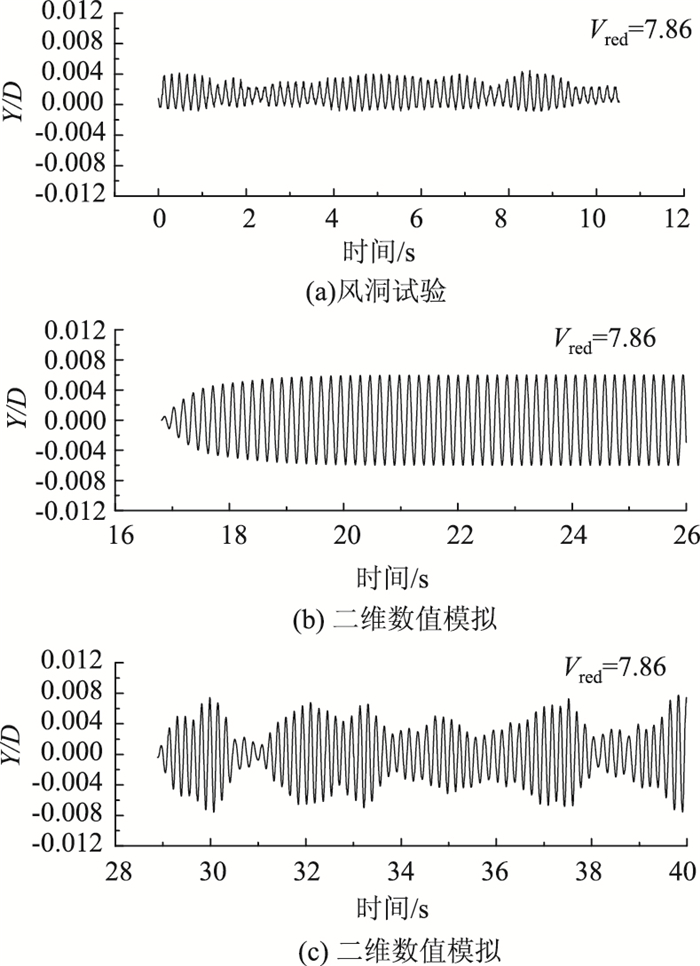
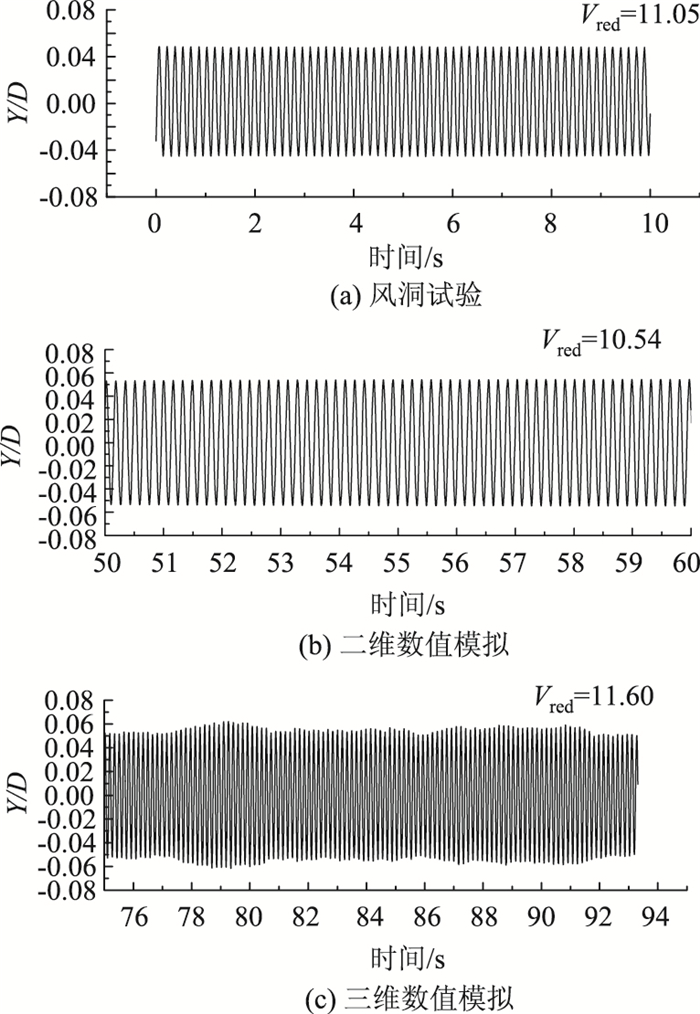
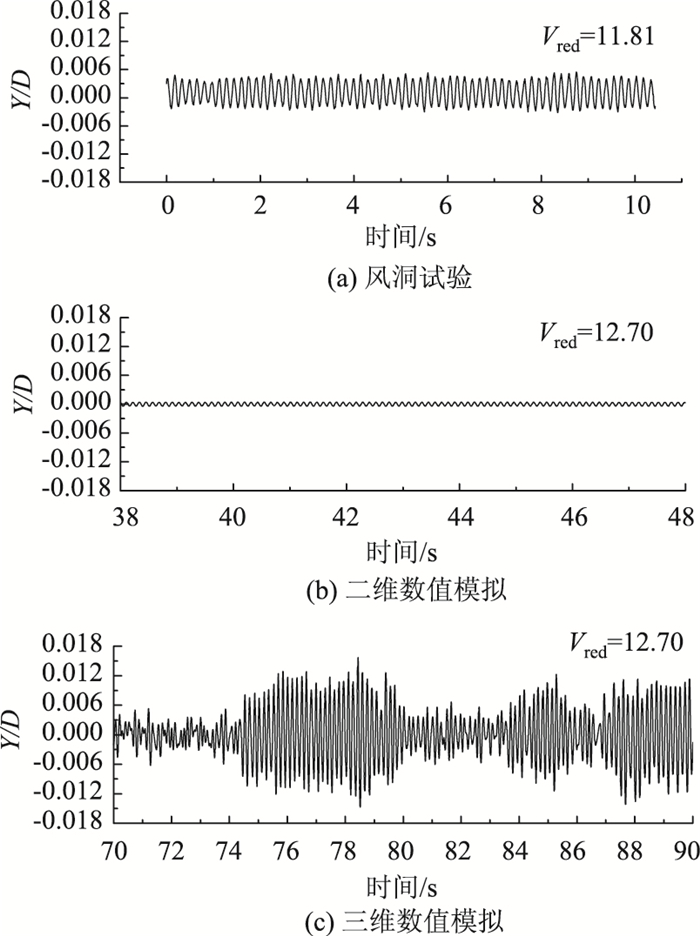
图 9~图 11所示为矩形断面竖向涡激振动“锁定区”起振点、最大振幅以及结束点对应的风洞试验、二维、三维数值模拟响应时程曲线。从图 9~图 11中可以看出,3种方法所得到的涡振“锁定区”起振点、最大振幅对应的涡激振动响应时程大致接近;涡振“锁定区”结束点对应的涡激振动响应风洞试验结果与三维数值模拟结果较为接近,与二维数值模拟结果相差较大;矩形断面数值模拟结果与风洞试验结果总体较为吻合。
|
| 图 9 涡激振动锁定区起振点对应的响应时程 Fig. 9 Response time history of VIV at start point in lock-in area |
| |
|
| 图 10 涡激振动锁定区最大振幅对应的响应时程 Fig. 10 Response time history vs. maximum amplitude of VIV in lock-in area |
| |
|
| 图 11 涡激振动锁定区结束点对应的响应时程 Fig. 11 Response time history of VIV at end point in lock-in area |
| |
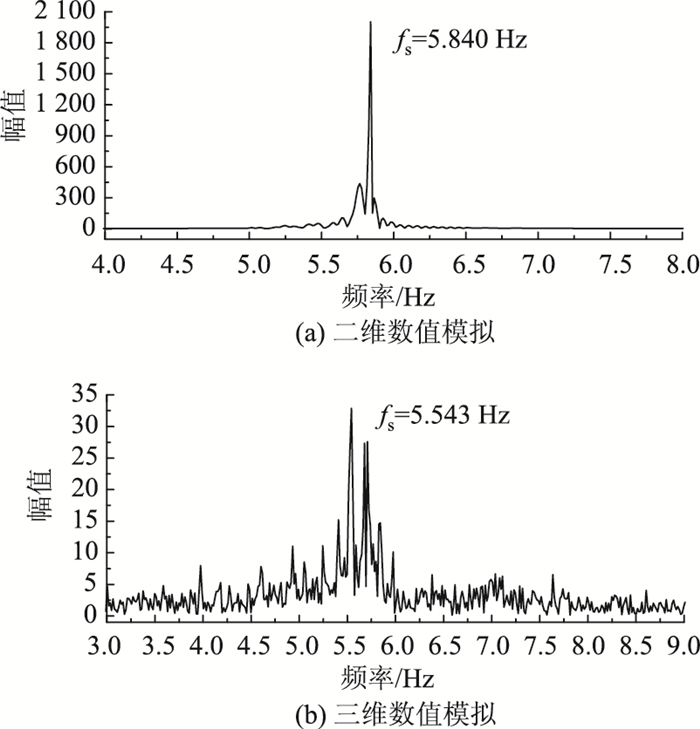
图 12~图 14所示分别为矩形断面竖向涡激振动“锁定区”起振点、最大振幅以及结束点对应的二维、三维数值模拟所得到的升力系数幅值频谱曲线。从图 12~图 14可以看出二维矩形断面柱体竖向涡激振动锁定区3个位置对应的升力系数幅值谱频率成份单一,而三维矩形断面柱体对应的升力系数幅值谱频率成份较多。从图 12中可以看出,二维、三维数值模拟结果显示矩
|
| 图 12 涡激振动锁定区起振点对应的升力系数幅值谱 Fig. 12 Amplitude spectrum of lift coefficients of VIV at start point in lock-in area |
| |
|
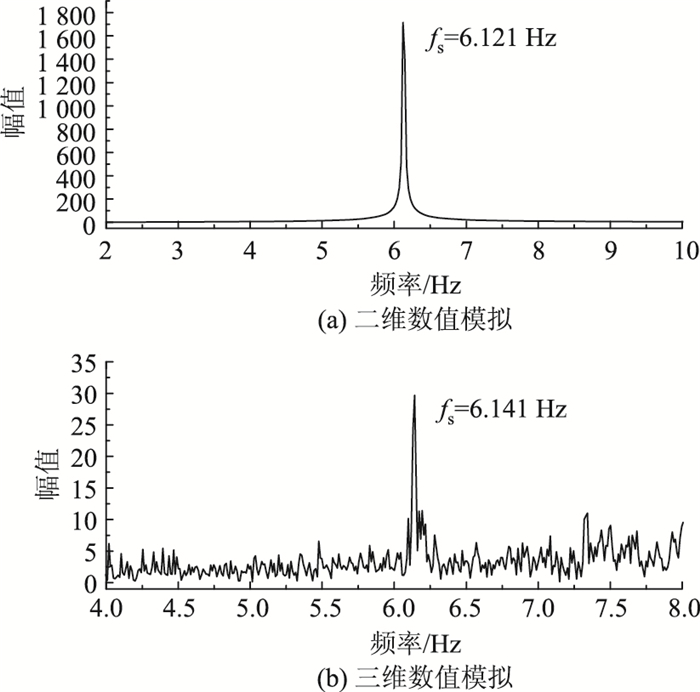
| 图 13 涡激振动锁定区最大振幅对应的升力系数幅值谱 Fig. 13 Amplitude spectrum of lift coefficients in lock-in area |
| |
|
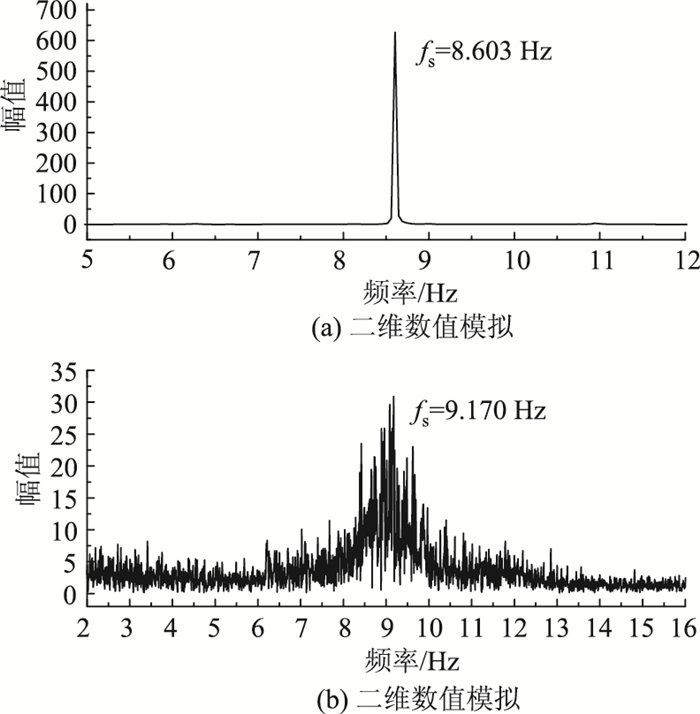
| 图 14 涡激振动锁定区结束点对应的升力系数幅值谱 Fig. 14 Amplitude spectrum of lift coefficients of VIV at end point in lock-in area |
| |
形断面柱体旋涡脱落频率分别为5.84 Hz和5.543 Hz,均低于结构自振频率,处于起振点位置。从图 13中可以看出,二维、三维数值模拟结果显示矩形断面柱体旋涡脱落频率分别为6.121 Hz和6.141 Hz,两者与矩形断面结构自振频率相近,表现为“锁定”。从图 14中可以看出,二维、三维数值模拟结果显示矩形断面柱体旋涡脱落频率分别为8.603 Hz和9.170 Hz,均大于矩形断面柱体自振频率,处于“锁定区”结束点位置。
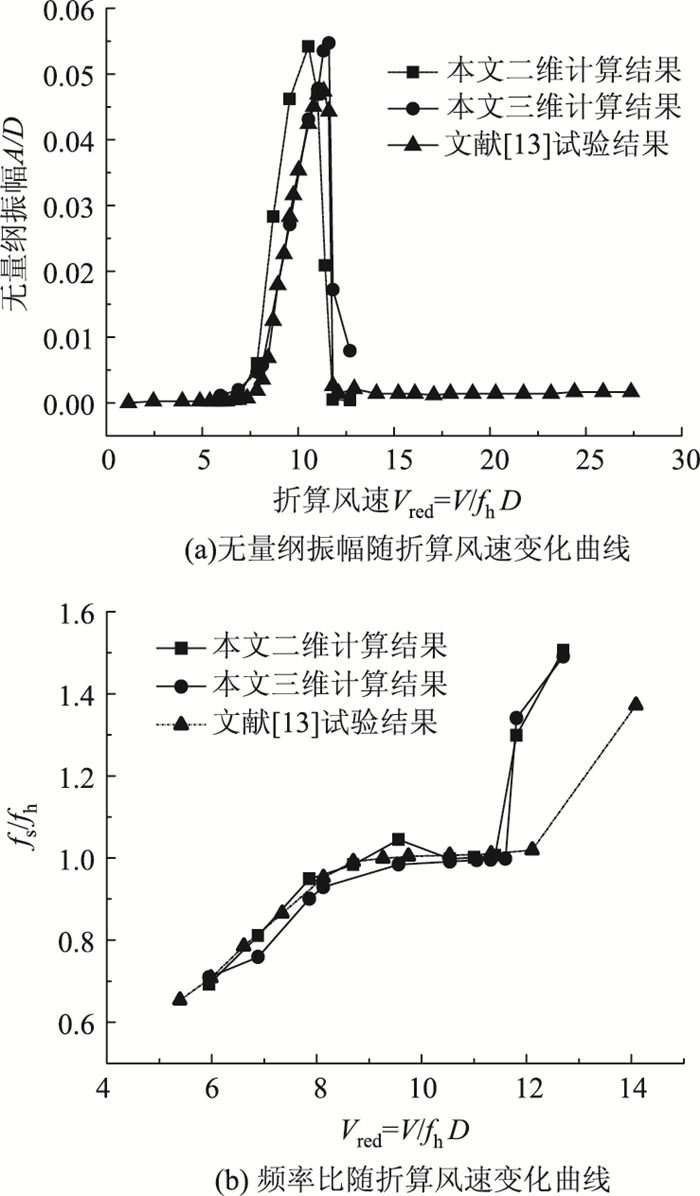
图 15所示分别为矩形断面竖向涡激振动振幅随折算风速的变化曲线以及漩涡脱落频率与结构振动频率之比随折算风速的变化曲线。从图 15(a)中可以看出,矩形断面柱体三维数值模拟所得的涡激振动锁定区与试验结果[13]较为吻合,二维模拟结果所得的涡激振动锁定区比试验结果略有提前;二维、三维数值模拟所得的最大无量纲振幅比较接近,比风洞试验结果偏大约15.5%。由图 15(b)可知,当折算风速为7.9~11.8时,矩形断面漩涡脱落频率与结构振动频率之比接近1.0,对应于矩形断面柱体涡激振动响应的“锁定”区。
|
| 图 15 矩形断面柱体竖向涡激振动响应计算结果与试验结果 Fig. 15 Numerical and experimental results of vertical VIV responses of rectangular cylinder |
| |
3 竖向涡激振动机理分析
分别从能量、涡激力与振动响应之间关系的角度对矩形断面柱体竖向涡激振动机理进行初步分析。定义不同折算风速下一个振动周期内涡激力所做的功为
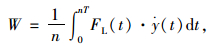
|
(10) |
式中,W为某折算风速下矩形断面柱体振动稳定时一个振动周期内涡激力所做功;FL(t)为t时刻作用在矩形断面柱体上的升力;ẏ(t)为t时刻矩形断面柱体运动速度;T为矩形断面柱体涡激振动周期;n为周期数。
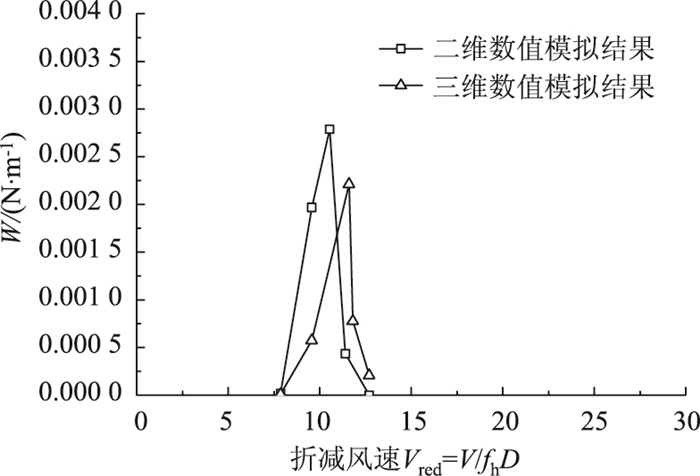
图 16所示为矩形断面柱体在不同折算风速下一个振动周期内涡激力所做功的二维数值模拟和三维数值模拟结果。由图 16可知,二维数值模拟和三维数值模拟计算得到的矩形断面柱体单个振动周期内涡激力所做功随折算风速的变化规律与矩形断面柱体无量纲振幅随折算风速变化规律接近;在锁定区起始点和结束点,涡激力在一个振动周期内所做功均较小,锁定区最大振幅处涡激力在一个振动周期内所做功最大。
|
| 图 16 不同折算风速下涡激力在一个周期内所做的功 Fig. 16 Work done by vortex induced force in a period at different converted wind velocities |
| |
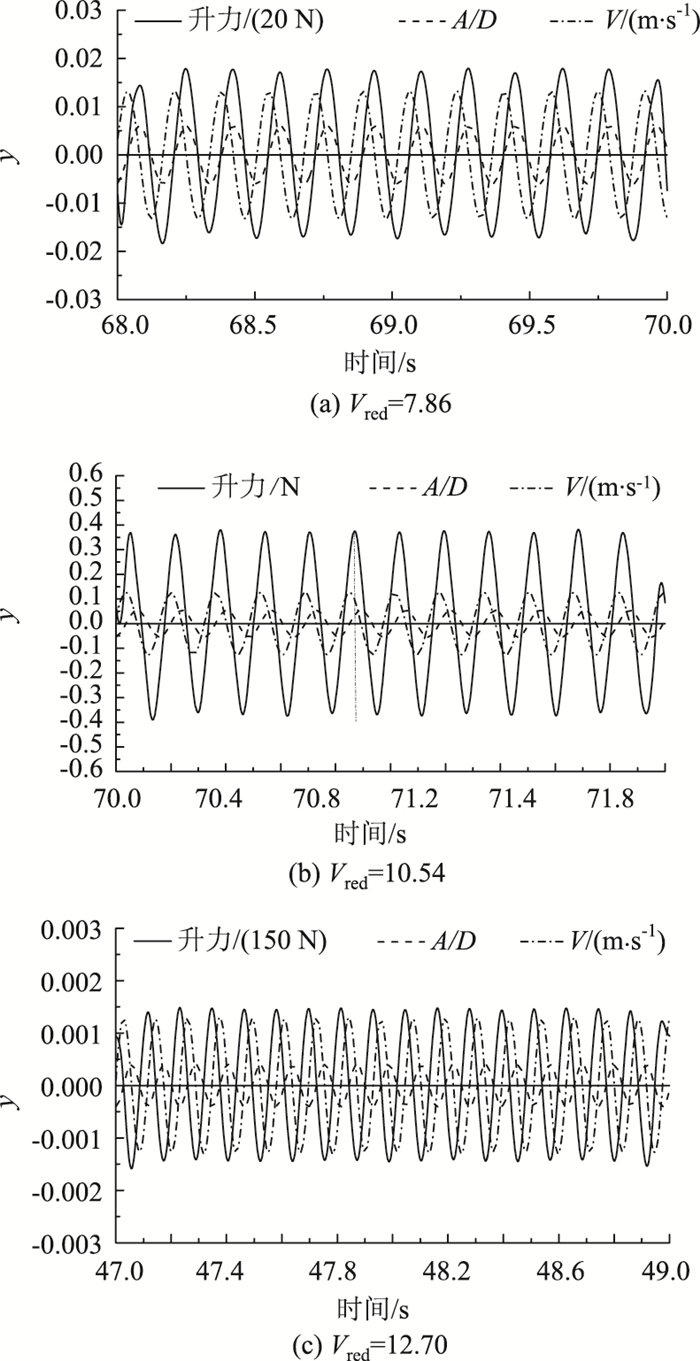
图 17、图 18所示分别为锁定区间不同位置矩形断面柱体涡激力、速度及位移响应二维、三维数值模拟结果。从图 17、图 18中可以看出,涡激振动锁定区起始点对应的涡激力时程与位移时程同相位,涡激力对结构做正功,结构振动能量增加,结构涡激振动的振幅逐渐增大;涡激振动锁定区最大振幅对应的涡激力时程与位移时程相位差约为45°,涡激力对结构做的功开始减小,结构涡激振动振幅不再进一步增大;涡激振动锁定区结束点对应的涡激力与位移时程相位差约为180°,表明涡激力对结构做负功,结构涡激振动振幅减小。
|
| 图 17 矩形断面柱体涡激力、速度及位移二维数值模拟结果 Fig. 17 Two-dimensional numerical simulation result of vortex-induced forces, velocity and displacement of rectangular cylinder |
| |
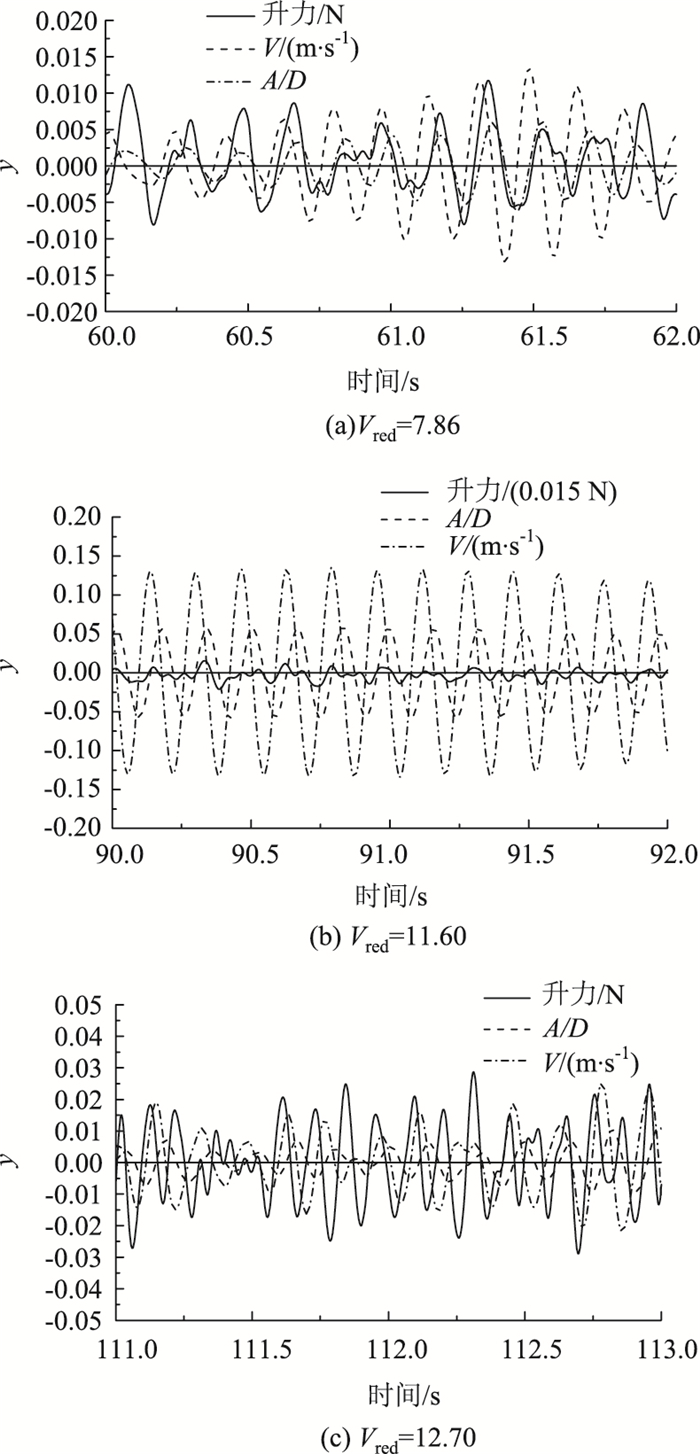
|
| 图 18 矩形断面柱体涡激力、速度及位移三维数值模拟结果 Fig. 18 Three-dimensional numerical simulation result of vortex-induced forces, velocity and displacement of rectangular cylinder |
| |
4 结论
针对工程结构中的涡激振动问题,采用“动网格+滑移网格”技术结合并行计算方法对矩形断面柱体进行涡振数值模拟研究,并与试验结果进行了比较,得到如下主要研究结论:
(1) 采用“动网格+滑移网格”技术可有效解决结构涡激振动数值模拟过程中可能产生的网格畸变、负体积等问题,提高结构涡激振动的模拟精度;
(2) 矩形断面柱体竖向涡激振动响应数值模拟结果与风洞试验结果总体吻合较好,三维大涡模拟结果优于二维数值模拟结果。
(3) 一个振动周期内涡激力所做功随折算风速的变化规律与无量纲振幅随折算风速的变化规律相似;涡激力与位移时程相位差随锁定区内折算风速的变化而变化,在锁定区起始点相位差为0°,振幅最大处相位差约为45°,锁定区结束点处相位差约为180°。
| [1] | BLEVINS R D. Flow-induced Vibration[M]. Malabar, Florida: Krieger Publishing Company, 2001 . |
| [2] | NOMURA T, NOMURA T. Finite Element Analysis of Vortex-induced Vibrations of Bluff Cylinders[J]. Journal of Wind Engineering & Industrial Aerodynamics , 1993, 30 (8) : 587-594 |
| [3] | NOMURA T. A Numerical Study on Vortex-excited Oscillations of Bluff Cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics , 1993, 50 : 75-83 |
| [4] | 曹丰产, 项海帆. 圆柱非定常绕流及涡致振动的数值计算[J]. 水动力学研究与进展:A辑 , 2001, 16 (1) : 111-118 CAO Feng-chan, XIANG Hai-fan. Calculation of Unsteady Flow around Circular Cylinder and Vortex-induced Vibration[J]. Journal of Hydrodynamics:Ser. A , 2001, 16 (1) : 111-118 |
| [5] | 徐枫, 欧进萍. 方柱非定常绕流与涡激振动的数值模拟[J]. 东南大学学报:自然科学版 , 2005, 35 (S1) : 35-39 XU Feng, OU Jin-ping. Numerical Simulation of Unsteady Flow around Square Cylinder and Vortex-induced Vibration[J]. Journal of Southeast University:Natural Science Edition , 2005, 35 (S1) : 35-39 |
| [6] | PAN Z Y, CUI W C, MIAO Q M. Numerical Simulation of Vortex-induced Vibration of a Circular Cylinder at Low Mass-damping Using RANS Code[J]. Journal of Fluids and Structures , 2007, 23 (1) : 23-37 |
| [7] | 方平治, 顾明. 高雷诺数条件下二维方柱涡激振动的数值模拟[J]. 同济大学学报:自然科学版 , 2008, 36 (2) : 161-165 FANG Ping-zhi, GU Ming. Numerical Simulation of Vortex-Induced Vibration for a Square Cylinder at High Reynolds Number[J]. Journal of Tongji University:Natural Science Edition , 2008, 36 (2) : 161-165 |
| [8] | 李永乐, 朱佳琪, 唐浩俊. 基于CFD和CSD耦合的涡激振和颤振气弹模拟[J]. 振动与冲击 , 2015, 34 (12) : 85-89 LI Yong-le, ZHU Jia-qi, TANG Hao-jun. Aeroelastic Simulation of Vortex-induced Vibration and Flutter Based on CFD/CSD Coupling Solution[J]. Journal of Vibration and Shock , 2015, 34 (12) : 85-89 |
| [9] | 刘志文, 周帅, 陈政清, 等. 宽高比为4的矩形断面涡激振动响应数值模拟[J]. 振动与冲击 , 2011, 30 (11) : 153-156 LIU Zhi-wen, ZHOU Shuai, CHEN Zheng-qing, et al. Numerical Simulation of Vortex Induced Vibration of Rectangular Cylinder with Aspect Ratio 4[J]. Journal of Vibration and Shock , 2011, 30 (11) : 153-156 |
| [10] | AL-JAMAL H, DALTON C. Vortex Induced Vibrations Using Large Eddy Simulation at a Moderate Reynolds Number[J]. Journal of Fluids and Structures , 2004, 19 (1) : 73-92 |
| [11] | SARWAR M W, ISHIHARA T. Numerical Study on Suppression of Vortex-induced Vibrations of Box Girder Bridge Section by Aerodynamic Countermeasures[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2010, 98 (12) : 701-711 |
| [12] | ZHAO Ming, CHENG Liang, AN Hong-wei, et al. Three-dimensional Numerical Simulation of Vortex-induced Vibration of an Elastically Mounted Rigid Circular Cylinder in Steady Current[J]. Journal of Fluids and Structures , 2014, 50 : 292-311 |
| [13] | 黄来科.矩形断面涡激力展向相关性试验研究[D].长沙:湖南大学, 2013. HUANG Lai-ke. Experimental Research on Span-wise Correlation of Vortex-induced Forces of Rectangular Cylinder[D]. Changsha:Hunan University, 2013. |
| [14] | 隋洪涛, 李鹏飞, 马世虎, 等. 精通CFD动网格工程仿真与案例实战[M]. 北京: 人民邮电出版社, 2013 . SUI Hong-tao, LI Peng-fei, MA Shi-hu, et al. Proficient in CFD Dynamic Grid Engineering Simulation and Case Study[M]. Beijing: Posts and Telecom Press, 2013 . |
| [15] | SCHEWE G. Reynolds-number-effects in Flow around a Rectangular Cylinder with Aspect Ratio 1:5[J]. Journal of Fluids and Structures , 2013, 39 (5) : 15-26 |
| [16] | SHIMADA K, ISHIHARA T. Application of a k-εModified k-εMODEL to the Prediction of Aerodynamic Characteristics of Rectangular Cross-section Cylinders[J]. Journal of fluids and Structures , 2002, 16 (4) : 465-485 |
 2016, Vol. 33
2016, Vol. 33
