扩展功能
文章信息
- 孙涛, 都培培, 郑松林, 张振东
- SUN Tao, DU Pei-pei, ZHENG Song-lin, ZHANG Zhen-dong
- 某型电动助力转向系统的多学科优化设计及操稳性能评价
- Multi-disciplinary Optimization for an Electric Power Steering System and Evaluation of Vehicle Handling Stability
- 公路交通科技, 2016, 33(7): 145-152,158
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(7): 145-152,158
- 10.3969/j.issn.1002-0268.2016.07.023
-
文章历史
- 收稿日期:2015-07-20
2. 机械工业汽车底盘机械零部件强度与可靠性评价重点实验室, 上海 200093
2. Key Laboratory for Mechanical Strength & Reliability Evaluation of Auto Chassis Components of Machinery Industry, Shanghai 200093, China
电动助力转向系统几乎已成为现代乘用车转向系统的标准配置,其性能的优劣直接决定着整车操纵稳定性和驾乘感受[1],但是,由于电动助力转向系统是复杂的机电耦合子系统,其设计、参数优化以及与整车的匹配受到众多机械与控制参数的影响和制约。近年来,众多品牌的乘用车都出现了各种各样的EPS系统问题,如通用雪佛兰MALIBU在行驶中EPS突然失去助力;宝马Z4和3系因EPS控制器内部电子元件设计存在缺陷导致助力中断;丰田锐志存在转向助力不足等。以上问题均导致汽车操纵稳定性恶化而被大量召回[2]。从系统工程角度来看,造成上述问题的根本原因是EPS系统参数优化设计与整车匹配存在缺陷,若能从系统工程分析的角度对EPS进行全局优化设计,势必可以极大地降低故障发生的概率,而针对EPS系统参数的优化设计选取必须通过综合考虑机械、控制参数的多学科全局优化方法得到,并通过整车操稳性的主客观评价方法进行匹配验证。
国内外学者针对上述问题进行一些研究。马涛峰等[3]分别从行驶系、转向系等方面研究影响汽车操纵稳定性的原因,最后得出转向系刚度、转向系传动比等6个参数对操稳性影响较大。Zhao Liu[4]利用伯德图法来显示EPS中不同参数对汽车的影响,得出EPS一些参数对整车稳定性具有一定的影响,并分析出几个对汽车操稳性影响较大的参数。当前对EPS一些参数进行优化的公开文献已有很多,并取得了一定的成效。B.I.Pryjmak[5]利用键合图法构建出汽车动力学模型,分析了电机转动惯量和车速对转向系统操纵稳定性的作用,而忽略了转向轴刚度等参数可能产生的影响。R.McCann[6]研究了轮胎侧偏刚度对操稳性的影响,但没有分析助力电机转动惯量、控制增益参数等对汽车操稳性的影响。赵万忠等[7]对机械参数进行了优化,忽略了控制参数优化。陈慧鹏等[8]将转向路感作为单一优化目标,并未考虑转向灵敏度对操稳性的影响。王伟等[9]通过加权系数法,将多目标优化问题转化为单目标优化问题进行优化,但这种方法是通过经验来估计每个目标函数所占的权重,具有一定的不准确性。
本文以国外开发中的某型电动助力转向系统为研究对象,针对其初始EPS设计及试验脉谱特性在整车操稳性试验中存在的问题,对该EPS系统机械参数和控制参数进行优化设计,以操纵路感和转向灵敏度为优化性能指标,分别通过遗传算法和粒子群算法两种优化方法进行多学科优化,得出Pareto最优解,并采用整车操稳性客观评价方法对优化设计的结果进行了时、频域匹配验证。
1 车辆系统建模由动力学分析,可得二自由度车辆模型和EPS模型:
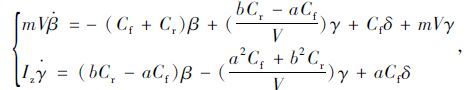
|
(1) |
式中,m为整车质量;V为车速;Cr,Cf分别为前后轮胎侧偏刚度;β为质心侧偏角;γ为横摆角速度;δ为前轮转角;a为前轮到质心的距离;b为后轮到质心的距离;Iz为车身横摆转动惯量。
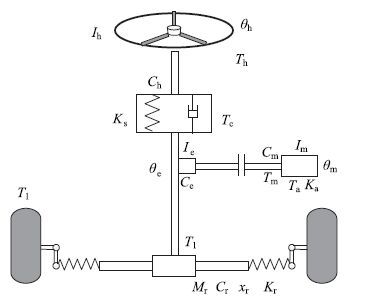
EPS系统结构简图如图 1所示。
|
| 图 1 EPS系统结构简图 Fig. 1 Schematic diagram of EPS system |
| |
分别对各部件进行受力分析,得到各自的运动方程:
转向柱:
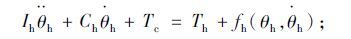
|
(2) |
助力电机:
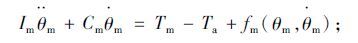
|
(3) |
输出轴:
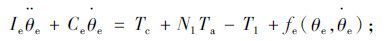
|
(4) |
齿条:
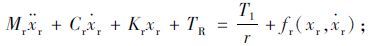
|
(5) |
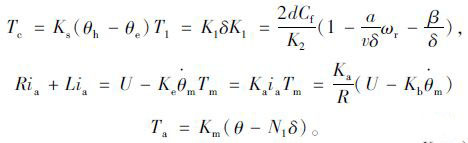
|
(6) |
上述式中,Ih为转向盘转动惯量;Ch为转向柱黏性阻尼;Tc为扭矩传感器测得力矩;Th为操纵方向盘力矩;Im为电机转动惯量;Cm为电机黏性阻尼;Tm,Ta为直流电机电磁转矩、电机输出助力矩;Ie为输出轴转动惯量;Ce为输出轴黏性阻尼;T1为转向阻力矩;Mr为小齿轮及齿条等效质量;Cr为齿条阻尼系数;Kr为等效弹簧系数;TR为路面随机干扰;θh,θm,θe分别为方向盘转角、电机转角和输出轴转角;N1,2分别为减速机构减速比、齿轮齿条转向器传动比;Ks为转向轴刚度;Ka为电磁转矩常数;K1为名义刚度;K2为从输出轴到前轮的传动比;ωr为横摆角速度;Km为电机刚性系数;Kb为电机反电势常数;ia为电枢电流;U为电枢电源电压;xr为齿条位移;R,L分别为电机的电阻和线圈电感; fh(θh,θ·h),fm(θm,θm),fe(θe,θ·e),fr(xr,x·r)为模型非线性等不确定因素。
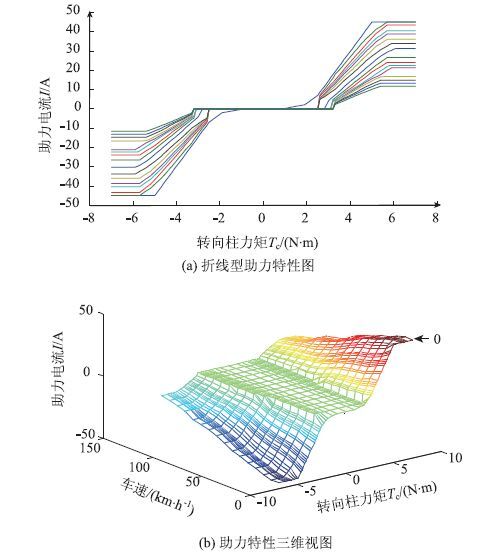
在EPS的工作过程中,助力特性决定ECU分配助力,控制电机运转的方式。合理的转向助力特性曲线不仅可保持汽车低速行驶时转向轻便灵活,而且可保持中高速行驶时的路感和操纵稳定性。该车初始设计采用的是折线形助力特性曲线图,见图 2(a),车速和转向柱力矩(由扭矩传感器测量)为输入量,通过试验得出助力特性曲线,最终确定电机的助力电流,进而计算出助力扭矩,实际助力特性如图 2(b)所示。
|
| 图 2 折线型助力特性图及其三维视图 Fig. 2 Piece-wise Curves and 3D view of assistance characteristic |
| |
2 优化目标的建立
EPS的最主要目的是提高汽车低速行驶时的转向轻便性和高速时的操纵稳定性。汽车的操纵稳定性是指汽车能遵循驾驶者通过转向系及转向车轮给定的方向行驶,且当受到外界干扰时,汽车能抵抗干扰而保持稳定行驶的能力。汽车转向操纵性能的评价指标有很多,如转向灵敏度、操纵路感和操纵稳定性等。转向灵敏度反映了车辆对驾驶员操作响应的快慢,对汽车的操纵稳定性非常重要。在本文中,为了更加直接客观地反映转向系统和整车系统的综合性能,拟采用横摆角速度与转向角之比r(s)/θh(s)来表示转向灵敏度,即车辆方向盘转角到车辆横摆角速度响应的传递函数表示。结合上面公式可知:
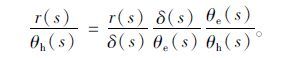
|
式(1)和EPS模型公式得转向灵敏度评价传递函数:
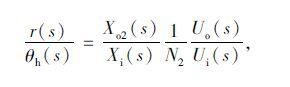
|
其中
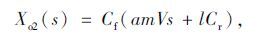
|
(7) |
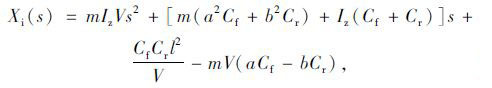
|
(8) |
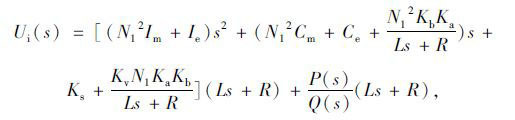
|
(9) |
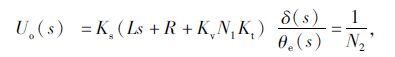
|
(10) |
式中N2为齿轮齿条转向器传动比。
对于路感的定义有多种,本文把路感定义为从负载力矩T1到驾驶员或机器人操纵手力Th的传递特性。在试验时常采取保持方向盘固定(相当于等转角转向,即θh=0),感受地面力,经转向系统传递到手上的力矩波动:
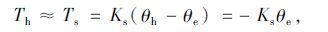
|
(11) |
求出操纵路感评价函数: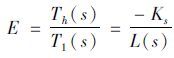
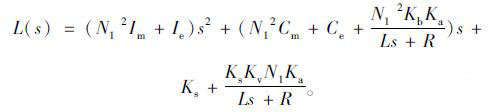
|
(12) |
相对于常规的汽车而言,转向稳定性取决于车速及固有参数。但随着EPS的装配,电机参数及转向轴刚度的变化将影响到转向稳定性,所以研究转向稳定性变得很重要。接下来将引入装配EPS系统的转向稳定性评价方法,并分析参数对其影响。
取转向灵敏度评价函数的分母为0,即公式中的N2·Xi(s)·Ui(s)=0, 再根据劳斯判据判断稳定性。估算知齐次多项式最高位6次,得系统的特征方程:
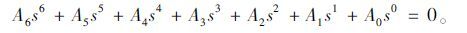
|
(13) |
各项系数为:
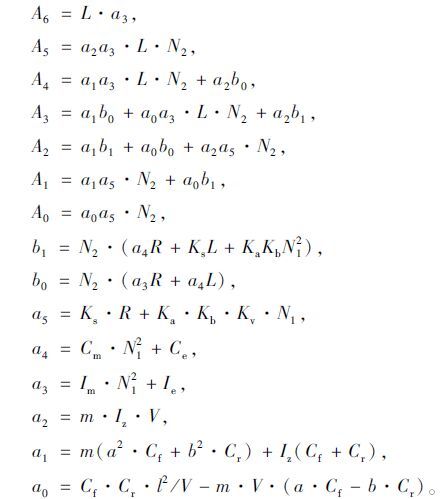
|
将系统特征方程的系数按下列形式排成Routh表:
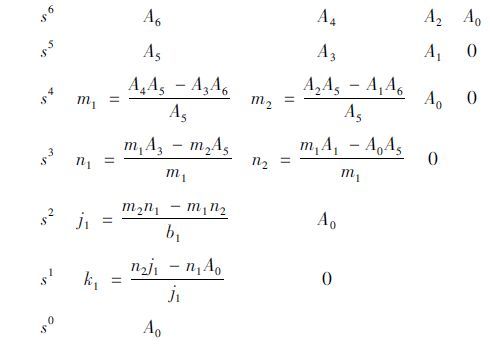
|
其中: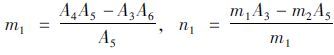
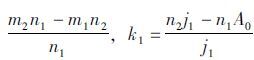
由劳斯判据的结论可得系统稳定的必要条件,即:A6>0;A5>0;m1>0;n1>0;j1>0;k1>0;A0>0。
3 EPS参数优化 3.1 目标函数的确定由文献[4]可知,EPS系统参数的优化问题实质上是一个多元多目标有约束的优化问题,影响其变化的参数有很多,考虑到实际的可行性。对转向轴刚度Ks、助力机构传动比N1、电机转动惯量Im和控制器中PID参数Kp,Ki,Kd进行优化设计。多目标优化问题的基本模型为:
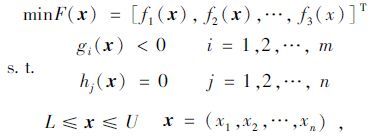
|
(14) |
式中,F(x)为目标函数;g(x)为不等式约束函数;h(x)为等式约束函数;x为决策矢量;L,U为x的上下界。
建立以操纵路感和转向灵敏度为目标函数的优化模型,操纵路感的频域能量:
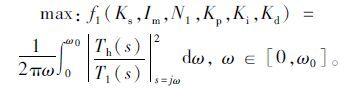
|
(15) |
转向灵敏度频域能量:
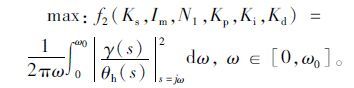
|
(16) |
由于优化算法中进行优化时是使目标函数最小化,所以取优化目标函数为:
目标函数1:min-f1(Ks,Im,N1,Kp,Ki,Kd);
目标函数2:min-f2(Ks,Im,N1,Kp,Ki,Kd)。
约束条件的确定,由于EPS优化的参数均为有实际意义的物理参数,故在开始优化前需确定其上下限。根据分析确定参数的上下界:
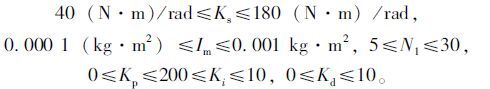
|
约束条件为:A6>0,A5>0,m1>0,n1>0,j1>0,k1>0,A0>0。
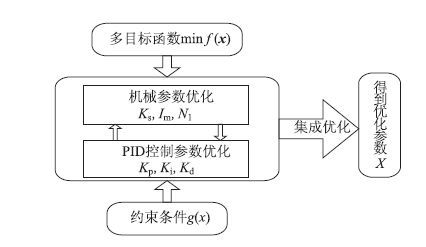
3.2 整体优化思路在传统的机电系统设计过程中,常将机械系统的硬件参数与控制系统参数分开优化,但EPS是一个高度协调的机电一体系统,为了能够更加提高转向系统性能并且减少能源消耗,本文提出协调优化,优化的框图如图 3所示。
|
| 图 3 集成优化框图 Fig. 3 Block diagram of integrated optimization |
| |
首先通过Simulink模型,求得一组名义系统参数,即Ks,N1,Im,Kp,Ki,Kd的初始值。设定系统在2 s内稳定,横摆角速度峰值在0.3左右,且增益幅度不超过20%的条件下,确定一组名义模型参数。具体优化步骤如下:
(1) 建立以操纵路感和转向灵敏度为目标函数的模型,将控制器参数取名义定值Kp=0.5,Ki=0.3,Kd=0.01,利用遗传算法和改进的粒子群算法进行优化机械系统参数Ks,N1,Im。
(2) 根据EPS控制和优化的需要,本文设计了PID控制器控制策略,将机械结构参数取名义定值N1=20,Im=0.000 5,Ks=60,优化控制器参数Kp,Ki,Kd。
(3) 将机械结构参数和控制系统参数同时设为自变量,利用两种算法进行协同优化,代入simulink模型进行验证并比较最终优化效果。
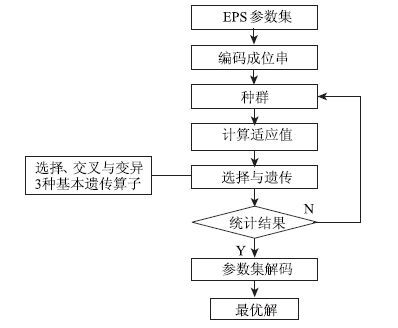
3.3 遗传算法优化遗传算法(genetic algorithm,GA)是一种进化优化算法,是将获取问题的最优解模拟成一个生物的进化过程来进行求解。图 4为遗传算法流程图。
|
| 图 4 遗传算法流程图 Fig. 4 Flowchart of genetic algorithm |
| |
机械参数和控制参数的优化:
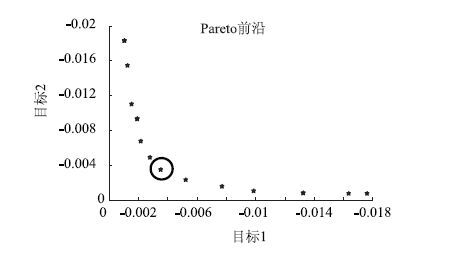
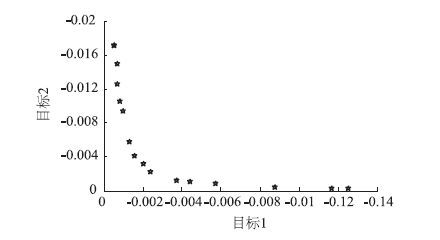
图 5和图 6分别为机械结构参数和控制参数多目标优化图,横轴为转向路感频域能量值,纵轴为转向灵敏度频域能量值。由于转向灵敏度反映的是转向系统的正效率,即输入端变化导致输出端变化,而操纵路感反映的是转向系统的逆效率,即输出端变化导致输入端变化,两者存在一定的矛盾,良好的转向灵敏度意味着较差的路感,故两能量值在取最优值时是相互冲突的,优化时就需要在两值之间进行适当的均衡处理,使两值均达到适度最优。MATLAB遗传算法工具箱在进行多目标优化时,优化结果常用Pareto图表示,Pareto前沿即Pareto最优化解的集合,当所得解越接近Pareto前沿,说明该解越趋于最优解。
|
| 图 5 机械参数多目标优化 Fig. 5 Multi-objective optimization for mechanical parameters |
| |
|
| 图 6 控制参数多目标优化 Fig. 6 Multi-objective optimization for control parameters |
| |
数学转换后,确定6个决策变量的上下界,编写约束条件函数,及适应度函数。结果见表 1。
| 目标函数 | 机械优化 | 控制优化 | 集成优化 |
| 目标函数1 | -0.003 503 | -0.002 197 | -0.012 203 |
| 目标函数2 | -0.003 732 | -0.003 771 | -0.013 586 |
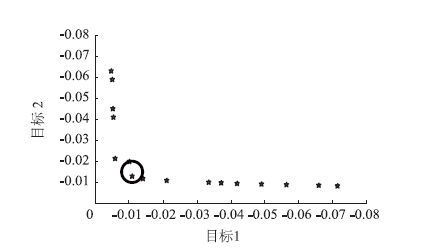
|
| 图 7 集成参数多目标优化 Fig. 7 Multi-objective optimization for integrated parameters |
| |
根据以上参数数据,将Kp,Ki,Kd固定不变,优化N1,Im,Ks可得目标函数的最优结果和优化后的机械参数。同理可得优化后的控制参数和相应的目标函数最优结果。将机械和控制参数集成优化,得集成优化结果和优化后参数。
根据所得数据可以看出:集成优化得到的目标函数分别是机械参数优化的3.484和3.64倍,是控制参数优化的5.554和3.602倍。这表明遗传算法集成优化使得操纵路感和转向灵敏度的均值都得到了一定的提高。
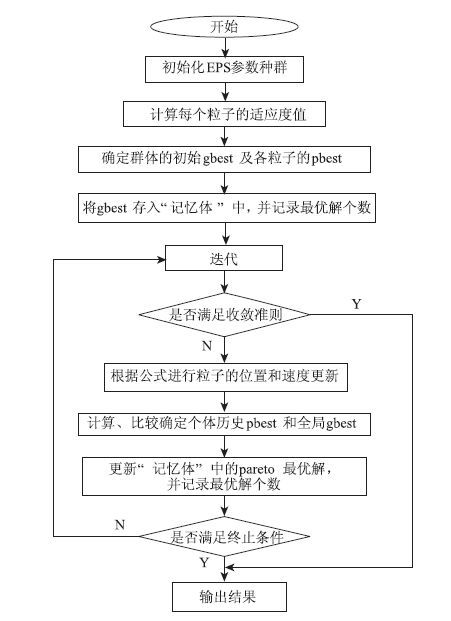
3.4 改进的粒子群算法优化粒子群算法(PSO)是一种基于群体的随机优化算法。它是通过粒子追寻搜索到的当前最优值来寻找全局最优值。单纯的粒子群优化很难解决多目标优化问题,本论文参考文献[10],参考其中的“记忆体”概念,通过不断记忆最优粒子,来寻找全局最优值,如流程图 8所示。更新各粒子速度和位置的公式为:
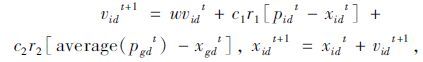
|
(17) |
|
| 图 8 改进的粒子群流程图 Fig. 8 Flowchart of improved PSO |
| |
式中,t为第t次迭代;d为决策变量的维数;average(pgdt)为对“记忆体”中当前最优Pareto解两两相互比较所得的较优粒子[10]。
机械参数的优化:
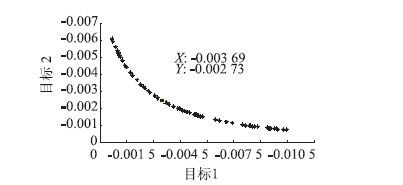
选取种群个数为100,w取值在[0.5,1.5]之间,c1,c2取值为2,r1,r2为介于0到1之间均匀分布的随机函数自动生成。根据前面已经计算出的目标函数和优化参数,结合改进的粒子群程序,运行得到最终优化结果,如图 9所示。
|
| 图 9 机械参数多目标粒子群优化结果 Fig. 9 Optimization result of mechanical parameters by multi-objective PSO |
| |
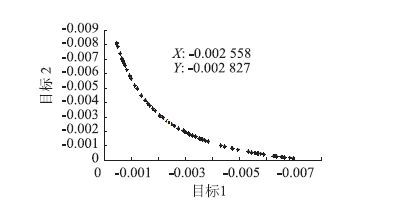
根据约束条件和适应度函数,得出多目标参数集成优化结果,如图 10所示。
|
| 图 10 控制多目标粒子群优化结果 Fig. 10 Optimization result of control parameters by multi-objective PSO |
| |
优化后得到表 2,根据所得数据可以看出:集成优化得到的目标函数分别是机械参数优化的3.74倍、4.55倍,是控制参数优化的5.39倍和4.40倍。这表明改进的粒子群集成优化使得操纵路感和转向灵敏度的均值在不同程度上都有了改善。
| 目标函数 | 机械优化 | 控制优化 | 集成优化 |
| 目标函数1 | -0.003 69 | -0.002 558 | -0.013 81 |
| 目标函数2 | -0.002 731 | -0.002 827 | -0.012 45 |
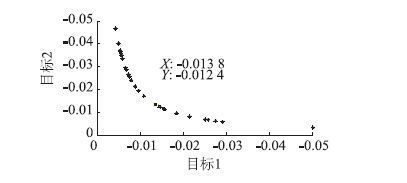
|
| 图 11 集成参数多目标粒子群优化结果 Fig. 11 Integrated optimization result by multi-objective PSO |
| |
4 操纵稳定性验证
关于转向操纵稳定性的试验评价,通常情况下在时域主要评价指标为质心侧偏角和横摆角速度[11]。对公式(1)进行零初始条件拉氏变换,得下述等式:
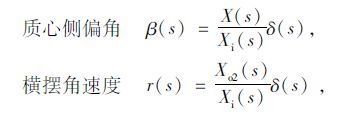
|
(18) |
式中,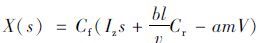
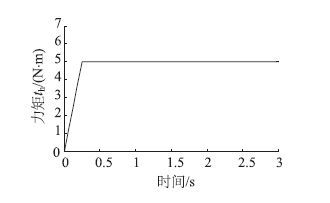
由于在实际工况中很难模拟方向盘阶跃响应,本论文以接近90°的斜率开始J-turn操作,图 12为方向盘输入力矩。
|
| 图 12 方向盘输入力矩 Fig. 12 Steering wheel input torque |
| |
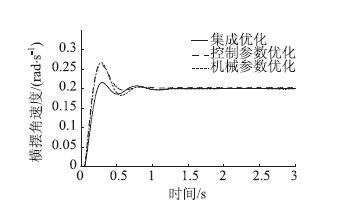
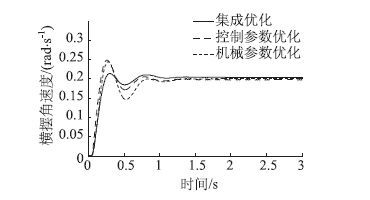
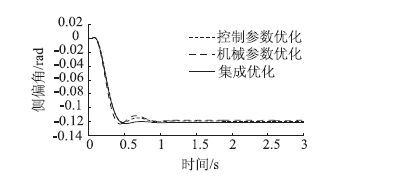
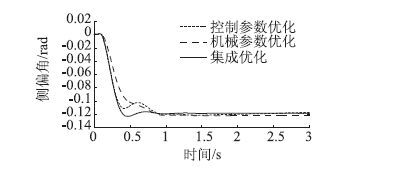
图 13~图 16为遗传算法和改进的粒子群算法优化结果,由图可知,经过集成优化后,与单独优化相比,两者的超调量明显降低,系统过渡过程时间进一步缩短,更快地由瞬态达到稳态,改善了转向系统的动态响应特性。
|
| 图 13 横摆角速度优化结果(遗传算法) Fig. 13 Result of yaw rate optimization (GA) |
| |
|
| 图 14 横摆角速度优化结果(改进的粒子群) Fig. 14 Result of yaw rate optimization (improved PSO) |
| |
|
| 图 15 质心侧偏角优化结果(遗传算法) Fig. 15 Result of sideslip angle optimization (GA) |
| |
|
| 图 16 质心侧偏角优化结果(改进粒子群) Fig. 16 Result of sideslip angle optimization (improved PSO) |
| |
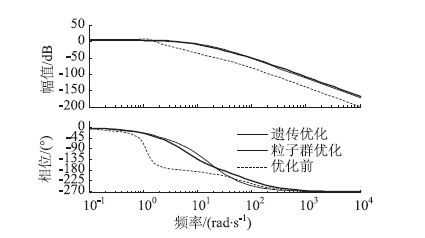
为了进一步从频域客观评价优化前后EPS对整车操纵稳定性的影响,文中采用了国际通用的操稳性四参数分析方法[11-12],得到了图 17的转向灵敏度幅频与相频特性曲线,由图可得表 3。
|
| 图 17 优化前后的转向灵敏度对比曲线 Fig. 17 Contrast curves of steering sensitivity |
| |
| 优化指标 | 优化前 | 优化后 (GA) | 优化后 (OPS) | |
| 横摆角速度增益/dB | 0.189 | 0.257 | 0.274 | |
| 共振峰频率/Hz | 1.18 | 1.31 | 1.37 | |
| 共振时增幅比b/a | 1.37 | 1.15 | 1.16 | |
| 横摆角速度峰值/稳态横摆角 速度=1/(2ζ) | 0.226 | 0.359 | 0.327 | |
| f=0.1 Hz | 0.023 | 0.003 | 0.010 | |
| 相位滞后角/(°) | f=0.6 Hz | -22.4 | -14.34 | -14.30 |
| f=1 Hz | -30.1 | -25.3 | -24.1 | |
由表 3可知:
(1)优化后的汽车稳态横摆角速度增益适度增大,共振峰频率变高,使转向操控更加清晰准确,整车操纵稳定性得到了提高。
(2)系统共振时,优化后的增幅比降低,车辆稳定性提高。同时,优化后转向灵敏度响应带宽分别约增加了0.515 7,0.526 8 Hz,带宽增大,系统响应速度提高。优化后系统阻尼比增大,超调量减小,幅频特性曲线较平缓,系统通频带宽增加,系统稳定性得到进一步提高。
f=0.1 Hz时优化前后的相位滞后角基本不变,均接近于0值,表明缓慢转向时,优化前后的转向特性基本不变;f=0.6 Hz时相位滞后角绝对值在优化后适当减小,表明优化后快速度转动方向盘时系统响应较快;同时,由f=1 Hz时相位滞后角绝对值优化后的减小可知以更快速度转动方向盘时,汽车响应速度得到进一步的提高。
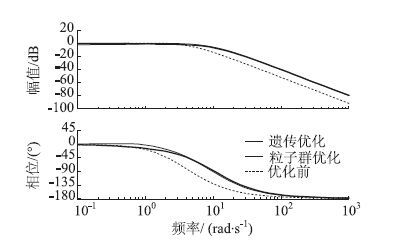
此外,由图 18转向路感幅频与相频特性曲线可知:
|
| 图 18 优化前后的转向路感对比曲线 Fig. 18 Contrast curves of steering road feeling before and after optimization |
| |
(1) 优化后的伯德曲线中频段增益平坦,相位和幅值裕度充足。优化后较优化前的相位裕度增加了19.1°,汽车操纵稳定性得到提高。
(2) 优化后带宽约增加了0.535 9,0.527 3 Hz,相位滞后减少,加快了系统响应速度。
5 结论(1) 基于转向操纵性能,建立多目标优化函数和约束条件,通过遗传算法和改进的粒子群优化算法得到了比原EPS系统更优的车辆操稳性能。
(2) 通过机械与控制多学科多目标协同优化方法对EPS系统进行集成优化,同时结合车辆操稳性分析的四参数评价验证方法,可以找到最优的EPS系统参数组合,最大限度降低了二者在运行情况下的相互作用和制约,使电动助力转向系统实现全局最优性能。
| [1] | ZENG Qun, HUANG Ju-hua. Modeling and Simulation of the Electric Power Steering System[C]//Pacific-Asia Conference on Circuits, Communications and Systems. Chengdu, China: IEEE, 2009: 236-239. |
| [2] | 费二威.电动助力转向系统匹配研究[D].长春:吉林大学,2014. FEI Er-wei. Matching Study of Matching of Electric Power Steering System[D].Changchun:Jilin University,2014. |
| [3] | 马涛峰, 薛念文, 李仲兴. 对汽车操纵稳定性的影响因素分析及对操稳性的研究评价[J]. 机械设计与制造,2005, (4) :122–123. MA Tao-feng, XUE Nian-wen, LI Zhong-xing. The Analysis of the Influence Factors of Vehicle Handling and Stability and Study and Evaluation on Handling and Stability[J]. Machinery Design & Manufacture, 2005, (4) : 122–123 . |
| [4] | LIU Z, YANG J, LIAO D. The Optimization of Electric Power Assisted Steering to Improve Vehicle Performance[J]. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, 2003, 217 (217) : 639–646 . |
| [5] | PYJMAK B I. Simulation of Electric Power Steering Armature Inertia Effects on Vehicle SystemHandling Response Using BondGraph Technology[EB/OL]. [2015-06-20]. http://papers.sae.org/851639/. |
| [6] | MCCANN R, PUJARA L R, LIEH J. Influence of Motor Drive Parameters on the Robust Stability of Electric Power Steering Systems[C]//Power Electronics in Transportation.Dearborn, MI: IEEE, 1998: 103-108. |
| [7] | 赵万忠, 施国标, 林逸, 等. 基于遗传算法的EPS 系统参数优化[J]. 吉林大学学报:工学版,2009,39 (2) :286–290. ZHAO Wan-zhong, SHI Guo-biao, LIN Yi, et al. Parameter Optimization of EPS System Based on Genetic Algorithm[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39 (2) : 286–290 . |
| [8] | 陈慧鹏, 陈立平, 王君明, 等. 电动助力转向系统性能优化及参数研究[J]. 机械科学与技术,2010,29 (2) :146–152. CHEN Hui-peng, CHEN Li-ping, WANG Jun-ming, et al. Optimization of the Parameters and Performance of an Electric Power Steering System[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29 (2) : 146–152 . |
| [9] | 王伟, 云浩. 电动助力转向系统参数研究及优化设计[J]. 中国工程机械学报,2014,12 (1) :28–33. WANG Wei, YUN Hao. Parametric Study and Optimal Design on Electric Power Steering Systems[J]. Chinese Journal of Construction Machinery, 2014, 12 (1) : 28–33 . |
| [10] | 宋冠英, 李海楠, 邹玉静. 一种基于Pareto 解集的无约束条件的多目标粒子群算法[J]. 制造业信息化,2008, (5) :141–143. SONG Guan-ying, LI Hai-nan, ZOU Yu-jing. A Multi-objective PSO Algorithm without Constraint Conditions Based on Pareto Optima Set[J]. Mechanical Engineer, 2008, (5) : 141–143 . |
| [11] | MIMURO T, OHSAKI M, YASUNAGA H, et al. Four Parameter Evaluation Method of Lateral Transient Response [EB/OL]. [2015-06-20]. http://papers.sae.org/901734/. |
| [12] | BAXTER J.Analysis of Stiffness and Feel for a Power-assisted Rack and Pinion Steering Gear[C]//SAE International Congress & Exposition. Detroit: SAE,1988: 827-833. |
 2016, Vol. 33
2016, Vol. 33
