扩展功能
文章信息
- 苏标, 阮梅洪, 王谦, 曹东源
- SU Biao, RUAN Mei-hong, WANG Qian, CAO Dong-yuan
- 新型城镇化模式下的离散交通网络设计模型与算法
- A Model of Discrete Transport Network Design and Its Algorithm under New Urbanization Mode
- 公路交通科技, 2016, 33(7): 130-136
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(7): 130-136
- 10.3969/j.issn.1002-0268.2016.07.021
-
文章历史
- 收稿日期:2015-09-14
离散型交通网络设计(discrete network design problem,简称DNDP)是指在投入资金有限的情况下,采用定量方法研究在已有路网上改扩建或新建某些路段的问题,属于交通规划的方案设计部分[1]。随着城镇化进程的加快,城镇中心较周边地区在人口、资源、环境等方面有更大的压力,也对交通规划工作提出了更为严格的要求。交通规划不仅需要从交通管理、交通投资的角度考虑,同时也需要考虑道路土地资源的集约、节约利用,并减少对周边生态环境的影响。
新型城镇化发展模式坚持以人为本,以新型工业化为发展动力,以集约高效、功能完善为发展特点,追求城镇发展与资源、环境、生态的协调。本文基于新型城镇化的发展理念,从不同区域对资源环境有不同限制程度的角度考虑,构建了区域差别化排放约束和区域差别化道路土地资源约束下的双层规划模型,以描述离散交通网络设计问题。其中,上层模型是在差别化约束下,寻求系统阻抗与投资费用的Pareto最优解;下层模型采用固定需求下的用户平衡配流模型描述用户出行的路径选择。为对构建的模型有效求解,采用Frank-Wolfe算法(简称F-W法)[2]求解下层规划模型,采用NSGAII求解上层规划模型;为避免算法陷入早熟收敛,采用第k小距离策略代替拥挤距离策略,并验证了设计算法的有效性。算例测试结果及区域范围的鲁棒性分析,表明本文构建的模型和算法可为中等规模路网规划提供借鉴。
1 优化模型 1.1 符号表示模型中使用的符号含义如下所示:
A为网络中路段a的集合;R为起点集合;S为讫点集合;xa为路段a的流量;X为路段流量向量;da为路段a的长度;Ka为路段a固有通行能力;Ka′为路段a单车道设计通行能力; ya为路段a的能力增量;Y为路段能力增量向量;ta(xa,ya)为路段a上的走行时间函数,是流量xa与能力增量ya的函数,采用BPR函数;Sa(xa,ya)为路段a上车辆的平均运行速度,是流量xa与能力增量ya的函数;qrs为点对(r,s)间的OD需求,r∈R,s∈S;fkrs为点对(r,s)间的第k条路径的交通流量,r ∈R,s∈S;δa,krs为路径关联变量,如果路段a在连接OD对(r,s)间的第k条路径上,δa,krs取1,否则取为0;
1.2 优化目标典型离散交通网络设计的优化目标主要从交通系统运行效率、资源节约及用户便利的角度考虑,由于交通网络设计问题是典型的领导者-追随者问题,已广泛应用双层规划模型描述此类问题[3-4],优化目标分述如下:
(1) 离散交通网络设计,首先要保证路网系统的总阻抗最小化,可用总行程时间最小化表示。由Wardrop第二原理[2]可知,路网系统总时间是路段流量向量与能力增量向量的函数,可表示如下:
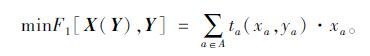
|
(1) |
(2) 从有限资金的角度考虑,在无投资费用约束的情况下,应以投资费用最小化作为优化目标。由于投资费用与改扩建路段的长度、宽度有关,因此整体投资费用是路段能力增量向量的函数,可表示如下:
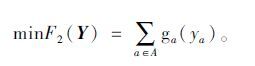
|
(2) |
(3)下层模型从用户出行便利性的角度考虑,采用固定需求下的用户平衡模型,其目标函数如下:
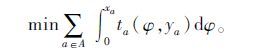
|
(3) |
一般认为此目标函数只是一种数学手段,不作直观或经济意义上的解释。
1.3 约束条件 1.3.1 上层模型约束条件(1) 区域差别化尾气排放约束
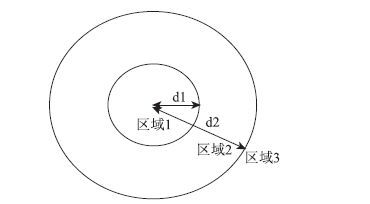
新型城镇化对生态环保要求更高,城镇中心区较周边地区有更为严格的机动车尾气排放要求,使机动车道单位面积的尾气排放广义费用呈现区域差别化。不同区域划分图见图 1。
|
| 图 1 不同区域划分示意图 Fig. 1 Schematic dcagram of region partition |
| |
区域i机动车道单位面积的广义排放费用:
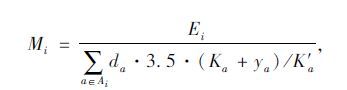
|
(4) |
式中,Ai为区域i的路段集合,i=1,2,3;3.5为单车道宽度。Ei为区域i的广义排放费用,表示如下:
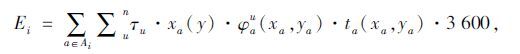
|
(5) |
式中,τu为污染物u的单位广义排放费用,n为排放物的种类数。φau为路段a上第u种污染物的排放因子,单位为g/(veh·s),表示如下:
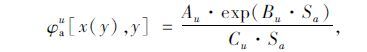
|
(6) |
式中,Au,Bu,Cu为排放参数,路段a上平均速度Sa表示如下:
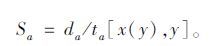
|
(7) |
机动车尾气排放主要成分为NOx,VOC,CO,其排放相关参数[5-6]见表 1。
| 排放物 | NOx | VOC | CO |
| Au | 1.571 8 | 2.784 3 | 3.396 3 |
| Bu | 0.040 732 | 0.015 062 | 0.014 561 |
| Cu | 10 000 | 10 000 | 1 000 |
| τu(EURO/kg) | 13.80 | 2.95 | 0.01 |
新型城镇化模式下,中心地区较周边地区有更高的生态环保要求,认为三区域机动车道单位面积的广义排放费用存在如下关系:
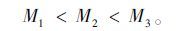
|
(8) |
(2) 区域差别化道路土地资源约束
新型城镇化发展模式要求集约、节约利用土地,城镇中心区的土地资源较城镇外围地区要求更为严格,即土地资源约束表现出差异性。道路用地资源与路段的长度、可拓宽的宽度有关。针对新增车道改扩建的情况,由于通行能力是按车道增加扩容,因此不同区域路段改扩建的能力增量为路段固有能力的倍数,即:
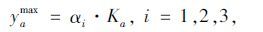
|
(9) |
式中,yamax为按规划通行能力增加的量;αi为区域i的能力增量参数,应由中心城镇向外围递增。
(3) 对于无预算约束的离散型交通网络设计上层规划模型,从DNDP含义的角度,路段能力增量的取值范围如下:
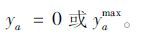
|
(10) |
下层模型由交通流守恒条件和非负约束条件,可得路段流量的约束条件如下:
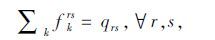
|
(11) |
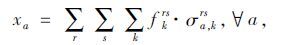
|
(12) |
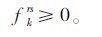
|
(13) |
对于相互冲突、矛盾的多个优化目标,不存在使各分目标同时取得最优的可行解[7]。而Pareto最优解是一组寻求多目标最优的折衷解,这组解的特点是在不弱化其他目标值的情况下,不可能再改进任一目标值。由于上层规划模型有两个优化目标,可采用Pareto最优理念构建上层模型。
由前文给出的模型优化目标函数及约束条件,基于Pareto最优解思想,构建了新型城镇化模式下的多目标离散交通网络设计双层规划模型如下:
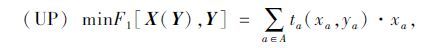
|
(14) |
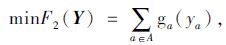
|
(15) |
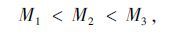
|
(16) |
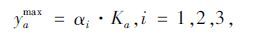
|
(17) |
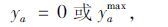
|
(18) |
xa=xa(ya)由下层模型求得:
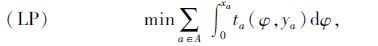
|
(19) |
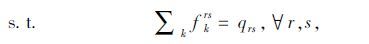
|
(20) |
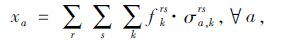
|
(21) |
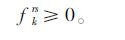
|
(22) |
由于本文构建的交通网络设计模型是多个目标同时优化求取折衷解的模型,而遗传算法具有并行搜索的特性,只需选择合适的遗传算子即可搜索到模型的近似最优解[8],与传统启发式算法相比求解过程更为高效。由于F-W算法可以有效求解用户平衡配流模型,NSGAII[9-10]已被广泛应用于求解多目标优化的Pareto优化解[11-12],因此本文结合F-W算法和NSGAII设计了求解前文构建双层规划模型的进化算法。
2.1 模型的算法设计遗传算法的编码方法采用0,1符号编码,个体编码的长度length等于决策变量的个数,即要改扩建路段与新建路段的个数之和。
步骤1:初始化参数设置。分别设置种群规模M,最大遗传代数T,交叉概率Pc,变异概率Pm,初始进化代数Gen=1。
步骤2:在差别化道路土地资源约束条件对应搜索空间内随机生成本代初始种群pop,对每个个体,采用F-W法[2]计算下层UE模型得到路段流量向量x1。针对pop中每个个体,分别求解三区域单位面积排放的广义费用M1,M2,M3,并将满足M3-M2>0且M2-M1>0的个体作为本代最终个体集s的个体。判定s是否等于规模M,若是,将得到的s个个体作为本代最终个体,并得到对应的本代最终流量向量x2,转向步骤3;若否,转向步骤2。
步骤3:针对本代最终个体,分别计算两目标值,进行非支配排序,并计算每个个体的拥挤距离。若Gen>1,则采用精英保留策略选择进化个体。对本代当前个体进化操作得到下一代种群qpop,具体进化操作如下:
(1) 选择算子,拥挤比较算子与随机联赛选择相结合的操作算子;
(2) 交叉算子,采用双点交叉操作算子;
(3) 变异算子,采用基本位变异操作算子。
步骤4:终止判断。若Gen<T,令Gen=Gen+1,转向步骤2,并将qpop赋值给pop,而不再随机生成pop;若是,终止算法转向步骤5。
步骤5:算法结束,输出第一个最优前沿F1作为决策值集,每个决策值对应的个体为路段规划决策方案。
算法的具体流程如图 2所示。
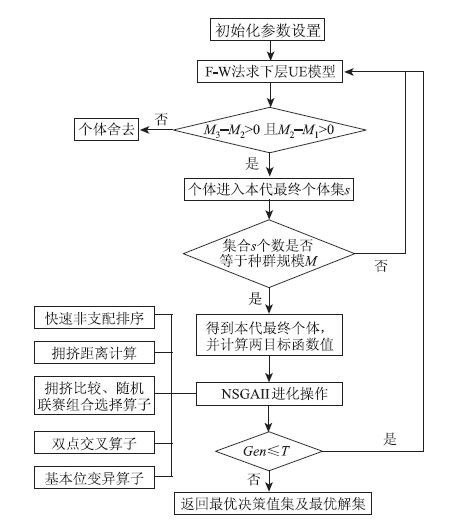
|
| 图 2 算法流程 Fig. 2 Flowchart of algorithm |
| |
2.2 算法验证设计
多目标进化算法的应用研究表明,NSGAII的拥挤距离仅在优化低维多目标优化问题时性能较好,说明拥挤距离的可解释性并不强[13]。而第k小距离作为一种最小邻里距离,是用欧式距离反映个体间的距离大小,已在第二代强度Pareto算法中广泛应用[14-15]。为避免前文设计算法出现早熟收敛,采用第k小距离代替设计算法中的拥挤距离,以验证设计的算法是否有效。
假设进化种群规模为N,外部集规模为N1,则种群中个体i与个体j间的距离可用两个体对应各目标值的欧式距离表示如下:
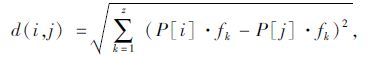
|
式中,z为目标维数,P[i]·f k表示个体i的第k个目标值。
将个体i 与进化群体及外部集中所有个体的距离升序排列,其中第k小的距离值即为个体i 的第k小距离,k常取进化群体与外部集规模之和的开平方值。
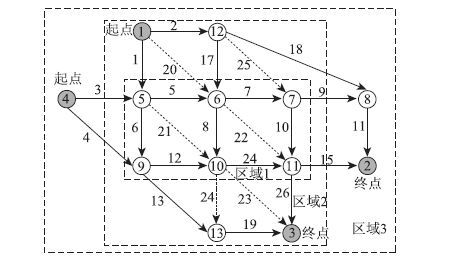
3 算例 3.1 算例参数设置本文在经典的Nguyen-Dupuis网络上(简称N-D网络)[16-17]划分不同区域,以测试本文提出的离散交通网络设计模型与算法。具体路网及区域划分见图 3。
|
| 图 3 路网图 Fig. 3 Road network |
| |
N-D网络图由13个节点,19条待改扩建路段(实线表示)和6条待新建路段(虚线表示)组成。节点1和4为交通需求的发生点;节点2和3为交通需求的吸引点。路段a上的行驶时间可采用BPR函数如下:
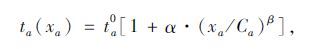
|
(24) |
式中,ta0为路段a的自由流走行时间,Ca为路段a的通行能力,参数α取0.15,β取4。
假设路段投资费用函数采用式(25):
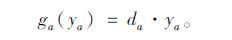
|
(25) |
假设节点12,6,10,13所在路段为N-D网络的主轴线,路段8为区域的中心,可将N-D网络距中心距离远近划分为3个区域:区域1包括路段5,6,7,8,10,12,14,21,22;区域2包括路段1,2,13,16,17,19,20,23,24,25;区域3包括路段3,4,9,11,15,18。
针对新增车道改扩建的情况,从土地资源区域差别化约束,假定区域1、区域2、区域3的能力增量参数α1,α2,α2分别取0.5,1.0,1.5,由固有通行能力与能力增量之和,可得到其规划通行能力。针对新建路段的情况,仍保持原N-D网络参数设置不变,则修改的路网参数如表 2所示。
| 路段 编号 | 路段长度/km | 自由流时间/min | 现状通行能力/(veh·h-1) | 规划通行能力/(veh·h-1) |
| 1 | 12 | 12 | 250 | 750 |
| 2 | 12 | 12 | 250 | 750 |
| 3 | 12 | 12 | 250 | 1 000 |
| 4 | 24 | 24 | 150 | 600 |
| 5 | 12 | 12 | 250 | 500 |
| 6 | 12 | 12 | 250 | 500 |
| 7 | 12 | 12 | 250 | 500 |
| 8 | 12 | 12 | 250 | 500 |
| 9 | 12 | 12 | 250 | 1 000 |
| 10 | 12 | 12 | 250 | 500 |
| 11 | 12 | 12 | 250 | 1000 |
| 12 | 12 | 12 | 250 | 500 |
| 13 | 24 | 24 | 150 | 450 |
| 14 | 12 | 12 | 250 | 500 |
| 15 | 12 | 12 | 250 | 1 000 |
| 16 | 12 | 12 | 250 | 750 |
| 17 | 12 | 12 | 250 | 750 |
| 18 | 36 | 36 | 150 | 600 |
| 19 | 12 | 12 | 250 | 750 |
| 20 | 24 | 24 | 0 | 250 |
| 21 | 24 | 24 | 0 | 250 |
| 22 | 24 | 24 | 0 | 250 |
| 23 | 24 | 24 | 0 | 250 |
| 24 | 12 | 12 | 0 | 500 |
| 25 | 24 | 24 | 0 | 250 |
结合算法的收敛性,经过多次对参数进行调试,最终确定遗传算法初始化参数设置如下:个体长度length=25,种群规模M=80,初始进化代数Gen=1,最大遗传代数T=500,交叉概率Pc=0.85,变异概率Pm=0.05,单车道设计通行能力K′a取250 veh/h。编码的前19位表示待改扩建的路段,后6位表示待新建的路段。每个基因座用符号1或0编码,1表示路段进行改扩建或新建,0表示现状路段不作改变。4个OD对间交通需求分别为q12=q42=350 veh/h,q13=q43=500 veh/h。
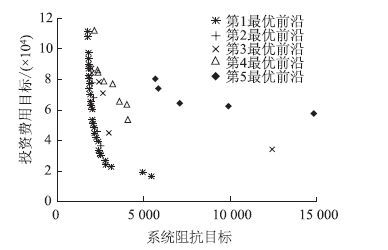
3.2 算例求解运行开发的Matlab程序,得到满足差别化排放约束和道路土地资源约束的37个优化解及其对应决策值。37个不同优化解即最终道路规划方案,受篇幅所限不再一一列出;截取决策值的前5个最优前沿如图 4所示。
|
| 图 4 NSGAII所得5个最优前沿 Fig. 4 Five optimal frontiers obtaineed from NSGAII |
| |
图 4中第一最优前沿的37个决策值对应37个最优规划方案。结合Pareto占优定义,第一前沿中的决策值为非支配解对应的决策值集,而其他前沿中的决策值均受前一前沿决策值支配。另外,第一前沿决策值集数量较多,表现出较广的分布性。
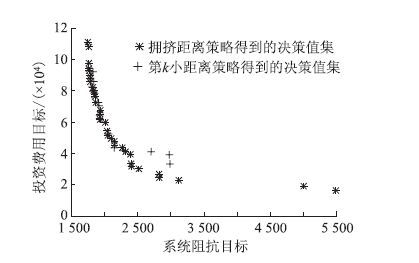
3.3 算法有效性的验算将第k小距离取代拥挤距离,运行Matlab程序,将得到的决策值集与拥挤距离得到的决策值集对比见图 5。
|
| 图 5 两种距离策略对应决策值集对比 Fig. 5 Comparison of Corresponding decision value sets of 2 distance strategies |
| |
由图 5可知,第k小距离策略得到的决策值多数与拥挤距离策略得到的决策值基本重合,少数受拥挤距离策略得到的决策值支配,且第k小距离得到的决策值分布范围较小。因此,对比结果说明NSGAII采用拥挤距离可以保证求取模型时解的收敛性和分布性,即验证了设计的算法可以有效求解构建的模型。
4 区域划分的鲁棒性分析由于前文得到的最优解集及决策值集是在一种区域划分基础上求取的,尚需分析约束强度区域范围变化对决策值的影响,以期为规划决策提供更为深入的借鉴。
情景1:将前文区域划分作为情景1。
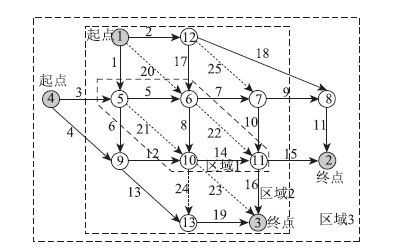
情景2:将区域1划分得更小,即土地、排放约束更为严格要求的区域更小,即将情景1中区域1的路段6,7,10,12划分到区域2,见图 6。
|
| 图 6 情景2路网图 Fig. 6 Road network of scenario 2 |
| |
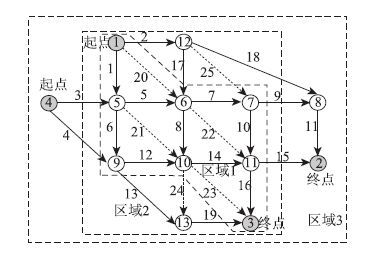
情景3:区域1划分得更大,即土地、排放约束更为严格要求的区域更大,即情景1中区域2的1,16,20,23划分到区域1,见图 7。
|
| 图 7 情景3路网图 Fig. 7 Road network of scenario 3 |
| |
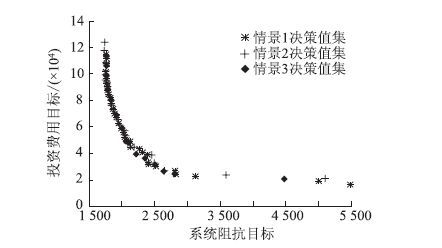
在Matlab程序中更改土地资源约束范围与尾气排放约束范围之后,得到3种情景的决策值集对比如图 8所示。
|
| 图 8 3种情景决策值集对比 Fig. 8 Comparison of decision value sets under 3 scenarios |
| |
由图 8可知,投资费用目标与系统阻抗目标是一组相互矛盾的目标,投资费用越高,系统阻抗越小。据中心区域划分大小的不同,可知情景2的中心区范围最小,情景1中心区范围次小,情景3中心区范围最大。据3种情景决策值集变化情况,得到如下两点分析结论:
(1) 投资费用大于4×104时,3种情景的投资费用目标值与系统阻抗目标值基本重合。这说明当投资费用较充裕时,同一投资费用决策值附近,3种情景的系统阻抗相差不大。
(2) 投资费用小于等于4×104时,3种情景的决策值集差异明显。
① 情景2的决策值集数量较情景1、情景3少,说明投资费用较低时,约束强度较高的中心区域范围越大,可选的路网规划方案越多。
② 同一系统阻抗目标时,情景2投资费用决策值最大,情景3与情景1的投资费用决策值重合,或情景3投资费用最小,即投资费用较低时,同一系统阻抗值附近,中心区域范围越大,投资费用越小。这说明在道路投资费用不足情况下,按规划车道条数较少情况建设,可在投资费用相对较小的情况下,达到相差不大的系统阻抗目标。
综上可知,投资费用较充裕的情况下,较强的区域差别化排放约束与道路资源约束范围大小变化,对投资费用与系统阻抗影响较小;投资费用不足情况下,较强的区域差别化排放约束与道路资源约束范围越大,可在投资费用相对较低情况下达到相同的系统阻抗,并且可选的规划方案更多。
5 结论为使交通规划工作与生态、资源相协调,基于新型城镇化发展理念,提出了区域差别化的排放约束和土地资源约束,构建了离散交通网络设计双层规划模型,其中上层模型采用Pareto最优思想处理双目标优化问题。在NSGAII基础上,设计了模型的求解算法,并在Matlab平台上开发了相应的算法程序。算例的测试结果及区域范围的鲁棒性分析表明,本文构建的模型与算法可为实际路网规划工作提供决策参考和借鉴。
| [1] | 刘灿齐. 预算约束的离散交通网络设计问题[J]. 中国公路学报,2002,15 (2) :90–93. LIU Can-qi. Discrete Network Design Problem with Budget Constraint[J]. China Journal of Highway and Transport, 2002, 15 (2) : 90–93 . |
| [2] | 陆化普. 交通运输规划理论与方法[M]. 北京: 清华大学出版社, 2006 : 179 -184. LU Hua-pu. Theory and Method in Transportation Planning[M]. Beijing: Tsinghua University Press, 2006 : 179 -184. |
| [3] | CHIOU S W. Bi-level Programming for the Continuous Transport Network Design Problem[J]. Transportation Research Part B:Methodological, 2005, 39 (4) : 361–383 . |
| [4] | 张小宁. 双层优化交通模型及其算法[J]. 同济大学学报:自然科学版,2005,33 (2) :169–173. ZHANG Xiao-ning. Bi-level Optimization in Transportation Analysis[J]. Journal of Tongji University:Natural Science Edition, 2005, 33 (2) : 169–173 . |
| [5] | LONG J C, SZETO W Y, HUANG H J. A Bi-objective Turning Restriction Design Problem in Urban Road Networks[J]. European Journal of Operational Research, 2014, 237 (2) : 426–439 . |
| [6] | MAYERES I, OCHELEN S, PROOST S. The Marginal External Costs of Urban Transport[J]. Transportation Research Part D, 1996, 1 (2) : 111–130 . |
| [7] | SOHN K. Multi-objective Optimization of a Road Diet Network Design[J]. Transportation Research Part A, 2011, 45 (6) : 499–511 . |
| [8] | 周明, 孙树栋. 遗传算法原来与及应用[M]. 北京: 国防工业出版社, 2005 . ZHOU Ming, SUN Shu-dong. Genetic Algorithms Theory and Applications[M]. Beijing: National Defend Industy Press, 2005 . |
| [9] | DEB K, MEMBER A, PRATAP A, et al. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6 (2) : 182–186 . |
| [10] | LI M M, LIU S M, ZHANG L, et al. Non-dominated Sorting Genetic Algorithms-Based on Multi-objective Optimization Model in the Water Distribution System[J]. Procedia Engineering, 2012, 37 (4) : 309–313 . |
| [11] | 唐云岚, 赵青松, 高妍方, 等. Pareto最优概念的多目标进化算法综述[J]. 计算机科学,2008,35 (10) :25–27. TANG Yun-lan, ZHAO Qing-song, GAO Yan-fang, et al. Overview on the Pareto Optimal-based Multi-objective Evolutionary Algorithms[J]. Computer Science, 2008, 35 (10) : 25–27 . |
| [12] | 公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J]. 软件学报,2009,20 (2) :271–289. GONG Mao-guo, JIAO Li-cheng, YANG Dong-dong, et al. Research on Evolutionary Multi-objective Optimization Algorithms[J]. Journal of Software, 2009, 20 (2) : 271–289 . |
| [13] | 刘厚才, 陈志钢. 非支配排序均匀遗传算法[J]. 计算机应用研究,2011,28 (11) :4020–4022. LIU Hou-cai, CHEN Zhi-gang. Non-dominated Sorting Uniform Generic Algorithm[J]. Application Research of Computers, 2011, 28 (11) : 4020–4022 . |
| [14] | 陈大山, 孙剑, 李克平. 基于SPEA2的城市快速路速度引导多目标优化[J]. 公路交通科技,2011,28 (10) :92–95. CHEN Da-shan, SUN Jian, LI Ke-ping. Multi-objective Optimization of Urban Expressway Speed Guidance Based on SPEA2[J]. Journal of Highway and Transportation Research and Development, 2011, 28 (10) : 92–95 . |
| [15] | 陆化普, 李悦, 蔚欣欣. 供给与需求不确定的离散交通网络设计模型[J]. 东南大学学报:自然科学版,2012,42 (6) :1221–1226. LU Hua-pu, LI Yue, YU Xin-xin. Discrete Traffic Network Design Model under Supply and Demand Uncertainty[J]. Journal of Southeast University: Natural Science Edition, 2012, 42 (6) : 1221–1226 . |
| [16] | 卞长志.需求不确定的离散交通网络设计模型与算法[D]. 北京:清华大学,2009:33-38. BIAN Chang-zhi. Model and Algorithm of Discrete Network Design Problem under Demand Uncertainty[D]. Beijing: Tsing Hua University,2009:33-38. |
| [17] | LO H K, TUNG Y K. Network with Degradable Links: Capacity Analysis and Design[J]. Transportation Research Part B, 2003, 37 (4) : 345–363 . |
 2016, Vol. 33
2016, Vol. 33
