0 引言

随着人民生活水平的不断提高和电子商务的迅猛发展，城市货运需求量的急剧增大使得货运交通在城市交通中的占比越来越大。研究货运车辆的出行行为、获得货运OD矩阵，对有效疏导与规划货运车辆的行车范围、合理分配城市道路交通资源具有现实意义。道路阻抗函数作为研究货运OD矩阵反推的基础，关系到整个反推过程中交通分配的准确与否。所以，将城市道路上的货车作为研究对象，合理地将城市道路上的客车对货车的影响作用表征出来成为继续研究后续问题的关键。

Bureau of Public Roads道路阻抗函数(以下简称BPR函数)模型是目前应用最多的计算道路阻抗的函数模型，该模型认为交通流饱和度对车流速度起确定性作用^[1]。由于它是根据高速公路的数据建立的，因此与城市道路的交通情况有所差异，在实际应用中应予注意。 H. Spiess^[2]就BPR函数中的模型参数β值过高和计算精度过低修正了BPR函数。K. B. Davidson^[3]利用排队理论，对Highway Capacity Manual (HCM)中的道路数据进行分析，提出了拥堵和非拥堵状态下道路阻抗的计算方法。我国学者提出用线性或非线性回归关系作为阻抗函数，该阻抗函数考虑了机、非之间的影响关系，比较符合我国机非混行的实际交通状况。王炜等^[4]根据交通流理论建立了车辆行驶速度与道路流量的理论模型。钟连德等^[5]基于我国城市快速路实测数据，对比了快速路交通流模型以及流量在不同车道分布与高速公路交通流特性的异同。

在针对性地研究货运OD矩阵时，需要将道路上的客、货车分开考虑，主要考虑的影响因素有客车对货车的影响、道路车道数、道路限速等因素，基于改进的BPR函数将路段上客车对货车的交通阻抗定量化地表达出来。

1 基本思路

路阻函数用数学式定量化地表达了交通阻抗。在货运OD反推过程中主要以货运车辆为研究对象，在使用TransCAD软件进行交通分配时，需要采用能够准确表征路网中路段阻抗情况的道路阻抗函数。在之前学者研究成果的基础上^[6-13]，考虑将实际交通出行路网中的客运车辆(包括私家车、微型车、公交车等)的交通负荷作为在路段上影响货运车辆行驶时间的主要因素，并将其视为各路段的背景交通量，建立针对路段上货运车辆的阻抗模型。对于模型中的系数，可根据道路交通量、通行能力和车速等数据采用最小二乘法来确定^[14]。

2 BPR道路阻抗函数分析

现行研究的城市交通路网中的阻抗主要是指交通成本(时间成本和费用成本)、交通时间、交通安全、舒适程度等因素。然而，综合考虑这些因素建立一个准确、严谨、科学的数学模型是非常困难的，而且运用起来也会因参数繁多而相当复杂难解。因此，通常采用条件假设和情景限定来简化研究内容。在众多专家大量理论研究和分析的基础上，现以BPR函数为基础进行道路阻抗模型研究。

2.1 BPR模型

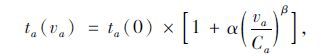
(1)

式中，t_a(v_a)为路段a上车流量为v_a时的车辆行驶时间；t_a(0)为路段a上车流量为零时的车辆行驶时间；v_a为路段a上的机动车流量；C_a为路段a的实际通行能力；α，β为系数，建议取α=0.15，β=4。

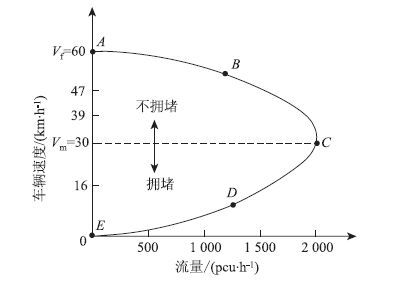
在利用TransCAD进行交通分配时，阻抗模型采用BPR函数，系数α，β可根据实际情况定义。图 1为速度-流量关系变化示意图，V_f为自由流时的车速；V_m为流量最大时对应的车速；A点、E点表示流量为0时对应的两种车速；B点、D点表示流量接近1/2最大流量时对应拥堵和不拥堵情况的车速；C点表示最大流量对应的车速。

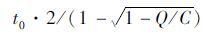
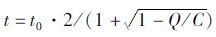
从图 1中可以看出，流量和速度之间的关系可表征道路的阻抗，即以流量为自变量，随着流量的增加出现车辆速度的变化。对于同一个交通量，在拥堵和非拥堵区域对应有两个车流速度，说明道路在这两个状态下的阻抗值不同。假设t₀为自由流时的车辆通过时间，Q为车流量，C为路段通行能力，当道路处于拥堵状态时，车流通过路段的时间为t=；当道路处于非拥堵状态时，车流通过路段的时间为；当Q/C=1时，t/t₀=2，即在路段处于饱和状态时，车辆的通行时间是自由通行时间的2倍^[15]。

美国BPR函数是理论回归模型。该函数主要考虑交通量的影响，较好地反映了阻抗的变化情况，且模型简单，使用起来比较简便，参数易于标定。

2.2 BPR函数用于货运OD反推的不足

(1) BPR函数只适于车流构成单一的情况，在针对货运OD矩阵的研究中，需要把调查的流量分为两类：客车流量、货车流量。有时还需根据研究情况将车型按大小细分。

(2) BPR函数主要针对高速公路小汽车，我国在对BPR函数重新标定运用于城市道路时，对于道路上出现的各种型号的货车，后期处理是将其直接折算为当量小汽车进行计算,这就将货车与小汽车之间的阻抗影响视为完全等同，但这与实际情况是不相符的。

(3) 对于货运量较大的路段，整体车流的速度应比直接将货车换算成当量小汽车的车流速度要小，但是BPR函数不能反映这一情况。

(4) 路段上客车数量增加时对货车速度的影响程度应低于路段上货车数量增加时对货车速度的影响程度，但BPR函数不能表征这一情况。

可以得出，若直接将BPR函数作为货运OD矩阵反推中使用的阻抗函数，存在着明显不足，需要针对性地研究以客车为主要因素对路段上货车产生的阻抗作用。

3 道路阻抗模型构造 3.1 客车流量的处理

研究货车的路段阻抗函数是为了在货运OD矩阵的反推过程中提供较为符合实际情况的货运车辆阻抗函数的计算方法。而货运OD矩阵反推的主要目的是研究现状货运OD矩阵，客运交通流量是已经发生过的现状流量，在每条路段上的交通量是固定的，不同于预测流量的分配。无论估计的货运OD矩阵如何变化，作为不参与分配的客运流量是保持不变的。对于已经发生在路段上的客运交通，属于背景交通量，客运流量虽然可以不参与分配和反推，但是流量的存在改变了路段阻抗，所以在进行道路货运交通研究的同时，需要把客运流量先加入到路段上去，将其视为路段的背景交通量，从而改变路段的实际阻抗。

3.2 构造路阻函数

路阻函数的影响因素众多，在有针对性地研究货运OD矩阵反推时，主要考虑的阻抗因素有：客车行驶产生的阻抗作用、道路类别(其道路限速有一定差别)、车道数、公交站点等，现主要分析路段上道路阻抗的变化情况。

为了反映客运流量对货运流量的阻抗作用，将加入客运流量后的路网阻抗作为初始阻抗，提出如下阻抗函数模型：

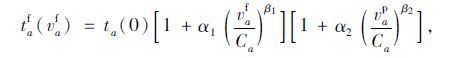
(2)

式中，t_a^f(v_a^f)为客车交通量为v_a^p、货车交通量为v_a^f时，路段a的整体行程时间；t_a(0)为交通量为自由流时，路段a的行程时间；C_a为路段a的通行能力；α₁，α₂，β₁，β₂为模型参数，可根据道路上客、货车的交通量、车速调查数据、道路通行能力等用最小二乘法确定，应根据不同城市的交通情况而定。

3.3 阻抗函数的特性

(1) 阻抗与客车流量成正比，即根据客车流量的增大，客车对货车的阻抗增大：

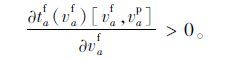
(3)

(2) 路段的阻抗值主要取决于货车自身的流量：

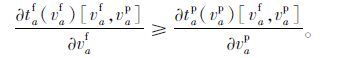
(4)

(3) 货车对客车的阻抗干扰强度大于客车对货车的干扰强度：

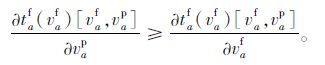
(5)

式(3)表示在客车和货车混行的路段，客车对货车的干扰作用是不可忽视的，而且干扰作用是一个单调函数，即随着客车量的增加，干扰作用也增加；式(4)和式(5)是符合现实的。在实际交通环境中，由于大货车与普通客车的车种性能、安全程度不同，导致了货车与客车驾驶员不同的交通心理状态及交通行为，反映到整个交通流状态上，就是货车对客车的干扰强度大于客车对货车的干扰强度，尤其是在以货车交通为主的交通结构下。

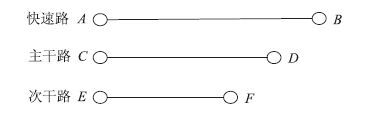
4 算例研究 4.1 道路阻抗函数标定

图 1为本文算例采用的道路类型和线路示意图。在从节点A到节点B(快速路)、从节点C到节点D(主干路)、从节点E到节点F(次干路)的路径上，当客运车辆作为背景交通量时，根据式(2)分别对货运车辆初始阻抗参数进行标定。

驾驶员在道路上的驾驶行为因其驾驶技术、心理特性、性别、年龄、工作等因素而存在差异，此处假设研究路段上的驾驶员是在正常情况下正常行驶，并假设：

(1) 节点之间的简化路径分别代表不同道路类别，即快速路、主干路、次干路。

(2) 路径忽略车辆通过交叉口时造成的延误阻抗。

(3) 参数标定所需数据(客、货车辆的速度、路径、行程、距离等)均为已知。

(4) 路径上行驶的客、货车辆数量均各自小于道路的通行能力。

现设定使用模型的约束条件为：城市快速路和没有交叉口或交叉口较少的城市一般路段(包括主干路和次干路)、以货运车辆为主的交通结构条件。其中节点之间的距离、货车速度和客车速度如表 1所示，节点之间的交通流量及通行能力如表 2所示。

根据已知数据，按照式(2)，采用SPSS软件进行拟合计算，其拟合系数结果如表 3所示。

算例采用的阻抗函数是将路段上的客车和货车区别分析，将客车量作为背景交通量，研究客车对路段货车的阻抗影响以及路段上货车之间的相互影响，综合得到路段的总阻抗，相对于单纯将机动车作为一个整体得到的阻抗要更为精确。

4.2 不同标定方式的结果比较

为了验证式(2)的道路阻抗适用于货运OD反推过程的分配模型，现将传统BPR函数的标定结果与式(2)所表示的路阻函数标定结果进行比较。同样采用SPSS对算例数据根据传统BPR公式进行拟合，结果如表 4所示。

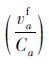
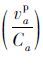
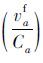
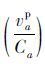
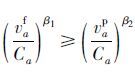
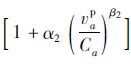
可以看出，BPR函数标定的参数β比式(2)的阻抗模型标定的参数β₂相差无几，而比参数β₁偏大。这是因为传统BPR函数将道路上的所有机动车作为一个整体，只单纯考虑了车流速度与饱和度之间的关系，而没有考虑其他影响因素，例如同向车流中客车对货车的影响以及货车与货车之间的相互影响。改进的BPR函数弥补了传统BPR函数模型中将货车和客车一视同仁的处理，在重点考虑货车为主时，区别对待客车和货车因车型、行驶速度等因素造成的阻抗延误的不同影响程度，即路段上的货车阻抗主要取决于货车自身的车流。这与前面所述的阻抗函数特性(2)是相符的。且改进的BPR函数还分析了客车对货车的阻抗影响，根据算例数据及假设条件(4)，特别是在以货车为主要交通流的道路上，有和均小于1；且有≥时，由表 4标定结果β₁值小于β₂值或β值(即β₁＜β₂或β₁＜β)，即,表明由客车造成的阻抗干扰小于货车造成的阻抗干扰，这与前面所述的阻抗函数特性(3)是相符的。通过比较可以发现，传统的BPR函数忽略了客车对货车的阻抗作用这部分造成的时间延误，而在式(2)中可看出，这一延误必然是大于1的。可见，改进的BPR函数相比于传统的BPR函数对路段阻抗的描述更为准确。

4.3 不同道路类型的标定结果比较分析

根据表 3可得到在算例中快速路、主干路、次干路针对货车的阻抗计算模型：

快速路：

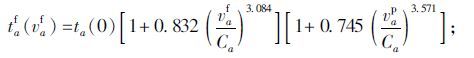
(6)

主干路：

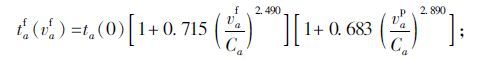
(7)

次干路：

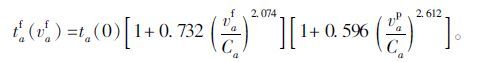
(8)

根据表 3中的拟合系数标定结果，对不同类型道路的阻抗模型进行对比。假设自由流时车辆速度相同，通过式(6)～(8)可以看出，随着道路等级的下降，客车对货车的阻抗作用表征参数β₂值也在下降，即随着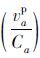的增大，车速增长的速度下降，这是因为随着道路等级的降低，道路限速也降低，道路的路面性质也改变。快速路有较少的平面交叉路口、公交站点等影响车流速度的设施，而且快速路一般与周边环境存在物理隔离，极大程度地减少了干扰车流的其他因素。主干路虽没有与周边环境隔离，但其道路基础设施相对完善(道路较宽，单向车道数多为3车道以上)，车速影响因素主要为公交站点(尤其是路中式公交站点形式)和平面交叉口。由于城市限货，城市货运车辆多出现在快速路和主干路上，所受干扰比次干路严重，根据标定结果可以看出这一变化趋势。可见，改进的BPR函数对于不同类型的道路在货运OD矩阵的反推过程中是适用的。

5 结论

通过改进传统BPR函数，并对算例的参数采取不同的标定方法进行分析，结果表明，改进的BPR函数计算结果更接近货运OD矩阵反推过程的实际路段阻抗情况。在实测的城市路网交通数据的基础上，在城市快速路或一般道路以货车为主要交通结构和忽略交叉口延误影响的情况下，可将改进的BPR函数运用于反推过程中的交通分配模型，获得货运OD矩阵的初步反推结果。但模型要在实际工作中得到应用，还需要对该模型进行更加深入的研究，例如，在除快速路以外的道路类型上分析阻抗的影响因素时，还应考虑在不限货的城市道路交叉口处以及交叉口处非机动车对货车的阻抗影响。