扩展功能
文章信息
- 何栋梁, 成彦惠, 方建勤, 柳群义
- HE Dong-liang, CHENG Yan-hui, FANG Jian-qin, LIU Qun-yi
- 考虑时空效应的隧道围岩变形分析
- Analysis of Deformation of Tunnel Surrounding Rock Considering Effect of Time and Space
- 公路交通科技, 2016, 33(7): 91-96
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(7): 91-96
- 10.3969/j.issn.1002-0268.2016.07.014
-
文章历史
- 收稿日期:2015-03-30
2. 湖南城市学院 城市管理学院, 湖南 益阳 413000 ;
3. 广东云梧高速公路有限公司, 广东 云浮 527300 ;
4. 中南大学 地球科学与信息物理学院, 湖南 长沙 410083
2. School of City Management, Hunan City University, Yiyang Hunan 413000, China ;
3. Guangdong Yunwu Expressway Co., Ltd., Yunfu Guangdong 527300, China ;
4. School of Geosciences and Info-physics, Central South University, Changsha Hunan 410083, China
隧道的变形可以认为是岩体流变特性参数和围岩应力状态的函数[1-3],并且隧道的开挖掘进和支护结构安装过程对围岩的应力状态有着强烈的影响[4]。隧道掘进对变形的影响主要是掌子面前未开挖岩体对于已开挖部分变形的限制作用,即当掌子面与研究断面非常接近的时候,掌子面对已开挖部分能够提供一些支护抗力,并且这一支护抗力随着掌子面和研究断面间距的增加而以递减的速率作用到衬砌上,所以掌子面与研究断面之间的距离多少决定着围岩荷载的释放率,围岩的荷载释放率影响其内在的力学行为特性、支护结构形变及力学性质和衬砌支护时机的选择。
为了有效发挥围岩自身承载能力确保隧道的稳定性,需对衬砌的合理加固时机进行确定,许多学者进行了相应研究[5-9],如辛全山等[8]利用二次耦合加固理论和现场监测结果,提出监测结果的变形转折点即为二衬加固的合理时间;荣耀[7]根据岩体应变能释放时间,给出了二衬的大致时间;张鹏等[9]利用芬纳公式和圆孔扩张理论,根据变形监测结果确定二次衬砌的合理加固时机。尽管以上这些研究给出了二衬衬砌加固时机的确定方法,但未考虑围岩特性和支护结构的相互作用关系。而在隧道开挖过程中,围岩将产生一定变形,为了限制围岩的变形,需构筑支护结构。此时,围岩的压力将分担给支护结构,而支护结构同样存在对围岩的反作用力,从而利用支护结构对围岩产生的径向约束力来控制围岩变形,防止围岩破坏。Sulem等[10]根据隧道围岩变形情况进行反馈设计提出的收敛限制法,采用地层特征线表征围岩承受的约束压应力同其实际变形之间的关系,考虑了围岩特性和支护结构的相互作用关系,从理论上解决了最佳支护设计问题。但Sulem等给出的隧道变形计算公式仅考虑了隧道变形的空间效应,未考虑时间对于隧道变形存在的影响。因此,为了同时考虑隧道开挖的时空效应,本文拟建立时间和空间效应共同作用下的隧道周边和拱顶位移,通过现场各部分围岩的变形监测,以依托某项目高速公路隧道为工程背景,进行隧道二衬加固时机的确定研究,拟为类似工程提供参考和借鉴。
1 工程概况与监测分析 1.1 工程概况以某高速公路隧道为工程背景,隧道围岩主要由砂岩和白云质灰岩组成,岩石较为破碎,存在一断层,围岩级别为V级。该隧道采用复合式衬砌,初期支护为锚喷支护,二衬为模注混凝土曲墙式,支护结构的具体尺寸见图 1,围岩的物理力学参数见表 1,隧道支护结构参数见表 2。
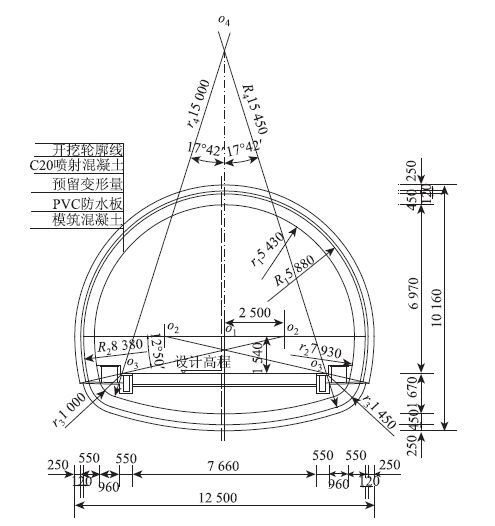
|
| 图 1 隧道横断面(单位:mm) Fig. 1 Tunnel cross-section(unit:mm) |
| |
| 围岩级别 | 弹模 E/GPa | 泊松比 μ | 重度 g/(kN·m-3) | 黏聚力 c/kPa | 内摩擦角 φ/(°) |
| Ⅴ级围岩 | 0.1 | 0.4 | 19.8 | 28 | 25.6 |
| 名称 | 弹模E/GPa | 重度γ/ (kN·m-3) | 截面积A/ mm2 | 惯性矩I/m4 |
| 系统锚杆 | 210.0 | 77.6 | 380 | — |
| 初衬 | 24.8 | 22.6 | 1 000 | — |
| 二衬 | 28.3 | 24.5 | 3 000 | 0.002 23 |
1.2 监测结果与分析
选取隧道的拱顶、拱腰等位置作为特征点,见图 2,分析相应的围岩和支护结构的内力和变形。
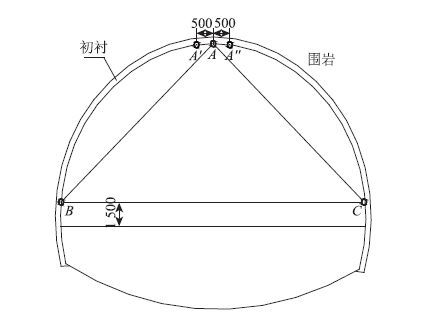
|
| 图 2 围岩隧道变形监测测点布置图(单位:mm) Fig. 2 Layout of tunnel surrounding rock deformation monitoring points(unit:mm) |
| |
图 3~图 7为隧道断面监测项目时程图,从图 3看出,拱顶下沉在开始阶段受上下台阶开挖的影响较为显著,这一阶段所形成的下沉量占总下沉量也较大,大约在开挖后第15天左右,上下台阶开挖的影响逐渐变小,参见图 3中第15~20天之间的曲线斜率明显减小;在第20天,下台阶开挖到监测断面所在位置,拱顶下沉曲线明显出现反弯;到第28天时,各开挖步骤的影响已趋于零。从图中还可以看出,当拱顶下沉平稳时,掌子面距离监测断面约60 m,下台阶距离监测断面约20 m,而仰拱的开挖对拱顶下沉的影响较小。由于开始阶段埋设测点被破坏,导致图 4中AC,BC测线前几天没有读数,但是从AB测线可以看出,前期下台阶和仰拱开挖皆处于停滞阶段时,AB线的收敛值发展较快,占到总收敛值的60%左右,因而上台阶开挖对于周边收敛的影响非常显著。第9天后下台阶开始施工,3条测线周边收敛量都有大幅度提高,但是从后面第19~30天的曲线可见下台阶和仰拱开挖对于周边收敛影响较之上台阶要小得多。周边收敛达到平稳时掌子面距离监测断面约60 m,下台阶距离监测断面约 20 m,所有这些都和拱顶下沉显现出同样的规律。图 5中前5天内由于上台阶开挖围岩压力增加迅速,达到总量的60%左右。在第14~15天,由于下台阶开挖至监测断面附近导致围岩压力突变,第31天围岩压力基本平稳。此时,距离掌子面为71 m,距离下台阶为20 m左右。超过该距离后施工对围岩压力的影响几乎不存在。从图 6可以看出初衬内力的发展规律基本上和围岩压力相似。由图 7可见:钢支撑开始阶段,外侧受到压力作用,且其因掌子面的推进而发展迅速;内侧开始阶段受到微小的拉应力作用,其对掌子面推进反应不是很敏感。第17天后,由于仰拱施工钢支撑内外力变化较为显著,该时期,外侧压应力继续增加,内侧逐渐由拉应力过渡到压应力。至35天钢支撑受力基本平稳。
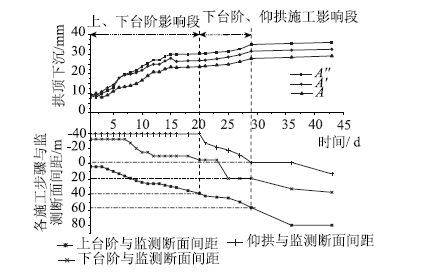
|
| 图 3 拱顶下沉时程图 Fig. 3 Time-histories of vault sink |
| |
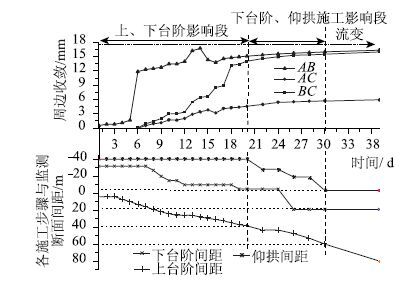
|
| 图 4 周边收敛时程图 Fig. 4 Time-histories of peripheral convergence |
| |
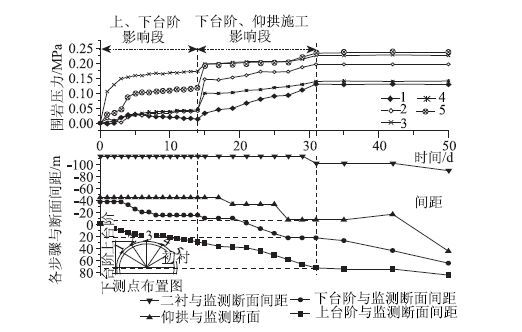
|
| 图 5 围岩压力时程图 Fig. 5 Time-histories of pressure of surrounding rock |
| |
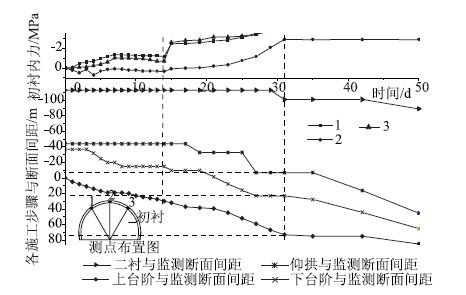
|
| 图 6 初衬内力时程图 Fig. 6 Time-histories of initial lining |
| |
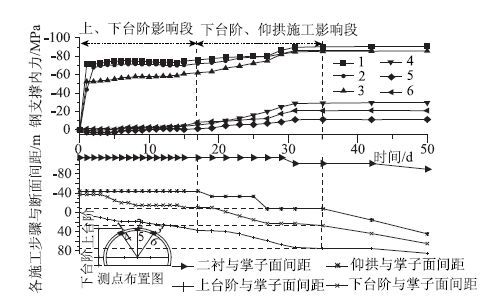
|
| 图 7 钢支撑内力时程图 Fig. 7 Time-histories of internal force of steel reinforcement |
| |
从表 3可见,在V级围岩中开挖隧道,周边位移收敛和拱顶下沉稳定时间约为30 d。根据欧阳建等[11],张周平等[12]的建议,由于V级围岩稳定性极差,周边位移收敛和拱顶下沉稳定时间可取上限值,即24天。另外,周边位移收敛和拱顶下沉达到稳定后,监测断面与掌子面之间的平均距离为67 m,同样可取上限值102 m。从围岩压力和初衬内力检测结果看,围岩和支护结构应力达到平衡所需时间及与掌子面间距都稍大于变形监测结果,能与变形监测结果形成映衬。
| 序号 | 埋深/m | 稳定时间/d | 掌子面与监测断面间距/m | ||
| 拱顶下沉 | 周边收敛 | 综合评定值 | |||
| 1 | 43 | 28 | 30 | 30 | 60 |
| 2 | 52 | 37 | 37 | 33 | 53 |
| 3 | 48 | 30 | 29 | 30 | 78 |
| 4 | 46 | 27 | 38 | 35 | 96 |
| 5 | 47 | 30 | 30 | 30 | 70 |
| 6 | 49 | 29 | 29 | 29 | 68 |
| 7 | 50 | 28 | 29 | 29 | 58 |
| 8 | 52 | 24 | 27 | 27 | 60 |
| 9 | 95 | 22 | 22 | 22 | 43 |
| 10 | 103 | 39 | 41 | 41 | 79 |
| 11 | 111 | 31 | 32 | 32 | 76 |
2 二衬时机的确定 2.1 考虑时空效应的隧道变形计算
Sulem等[10]根据隧道围岩变形情况,建立围岩特性曲线和支护特性曲线的相互作用关系,见图 8,从图中可以看出,在初始阶段,特征曲线呈现线弹性状态;当围岩变形量达到一定值后,逐渐出现塑性变形,此时,围岩可在较小的约束反力下即保持稳定,并且保持稳定所需要的约束力逐渐减小;当出现松动区时,表明围岩开始产生破坏,此时,若要保持围岩的稳定则需提供较大的约束力。
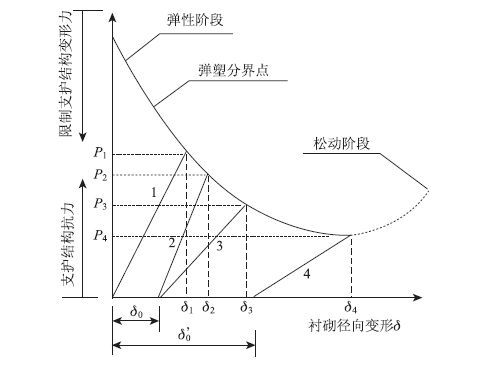
|
| 图 8 围岩与衬砌的相互作用 Fig. 8 Interaction of surrounding rock and lining |
| |
线段1表示隧道开挖后立即进行加固,在支护结构上产生的支护反力P1,此时,由于围岩在地应力作用下存储了一定的应变能,若立即进行支护则释放的能量较小,因此,支护结构上将承担较大的围岩压力。线段2,3表示围岩产生一定变形量δ0后再进行支护结构的施工,其中线段2表示的支护结构刚度大于线段3表示的支护结构的刚度。可见,刚度越大的结构可有效限制围岩变形,但同时由于刚度大将产生更多的附加工程费用。而刚度适当降低的支护结构,允许围岩有一定变形,但确保围岩的稳定性情况,从而有效达到支护围岩的目的,并且能够减少工程造价,达到优化支护的效果。线段4表示当围岩发生一定变形δ0时再进行支护,此时,围岩变形量达到了最大允许变形量,对于支护结构刚度的要求可进一步降低,并且支护结构上所承担的支护压力也达到最小值P4,因此,该时刻即为施工衬砌的最优时机。若支护结构提供的约束力无法达到P4,则岩体将产生塑性变形,产生松动区,并不断扩大,直到岩体出现失稳破坏。
从以上分析可以看出,收敛限制法采用地层特征线表征围岩承受的约束压应力同其实际变形之间的关系,支护限制线表示隧道开挖并产生一定变形后设置支护时,围岩对支护作用的地层压力和支护变形间的关系;地层特征线和支护限制线的交点表示围岩的变形已趋于稳定,因此,收敛限制法从理论上解决了最佳支护设计问题。
Sulem等[10]根据收敛限制法拟合得到隧道变形的计算公式:
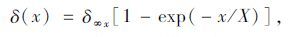
|
(1) |
式中,δ(x)为隧道周边或拱顶位移;δ∞x为由于施工过程中产生的隧道周边和拱顶位移;X为掌子面施工过程的影响距离,该值受隧道围岩的塑性半径R0的影响,X=aR0,a=0.84。
当隧道围岩处于弹性状态时,式(1) 的预测结果较好,但是,若围岩进入塑性状态,式(1) 的预测存在一定误差,因此,Sulem等[10]对式(1) 进行了修正:
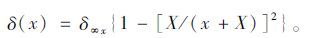
|
(2) |
从式(2)可以看出,其主要考虑了隧道变形的空间效应,但是在实际开挖过程中,往往时间对于隧道变形同样存在较大影响。因此,为了同时考虑隧道开挖的时空效应,本文将时间和空间效应得到的隧道周边和拱顶位移进行叠加,即通过时间-位移曲线和空间-位移曲线得到的结果进行相加,从而可得到考虑时空效应的隧道变形情况,
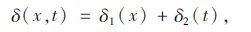
|
(3) |
式中,δ(x,t)为考虑施工时间和空间效应的隧道周边和拱顶位移;δ1(x)为不考虑时间效应的隧道周边和拱顶位移;δ2(t)为只考虑时间效应的隧道周边和拱顶位移。
根据式(3),可分别将δ1(x)和δ2(t)展开成如下形式,
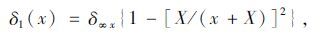
|
(4) |
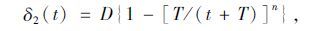
|
(5) |
式中,参数D与掌子面的推动距离x存在如下关系:
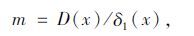
|
(6) |
从而可将式(3)进一步变化为,
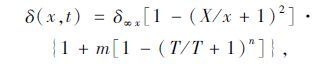
|
(7) |
式中,m,n 为待定系数。
式(7)中的5个参数,可以通过监测得到的位移进行计算,然后,可进一步得到x和t趋向某一值时,岩体的位移。
2.2 二衬支护时机的确定选择A点的下沉量和沿BC线的收敛量作为研究对象。该级别围岩中考虑流变和掌子面推进的共同影响,因而可采用式(7)结合实测值,反演其中的参数,得到其相应的参数,见表 4,从而可得到拱顶下沉稳定时,δ∞x的平均值为8.6 mm,X的平均值为23.5 m,m的平均值为23.2,T的平均值为40 d,n的平均值为4。周边收敛时,δ∞x的平均值为8.6 mm,X的平均值为24.4 mm,m的平均值为21.4,T的平均值为21 d,n的均值为4。
| 项目 | 测点号 | δ∞x/mm | X/m | m | T/d | n |
| 拱顶下沉 | A | 10.1 | 37.2 | 3.8 | 75.9 | 15 |
| A | 0.8 | 40.2 | 49.9 | 68.2 | 12 | |
| A | 8.6 | 16.8 | 3.3 | 59.9 | 14 | |
| A | 2.7 | 3.3 | 18.4 | 13.2 | 1 | |
| A | 13.6 | 14.7 | 13.2 | 11.9 | 1 | |
| A | 11.7 | 21.6 | 20.8 | 15.6 | 3 | |
| A | 3.1 | 16.9 | 57.4 | 78.7 | 10 | |
| A | 3.4 | 26.4 | 33.6 | 31.3 | 4 | |
| A | 23.3 | 34.0 | 8.0 | 6.5 | 1 | |
| 周边收敛 | BC | 0.3 | 29.7 | 22.8 | 19.2 | 2 |
| BC | 2.2 | 18.0 | 25.2 | 28.6 | 5 | |
| BC | 1.7 | 29.3 | 35.5 | 24.0 | 7 | |
| BC | 34.7 | 21.7 | 6.5 | 5.3 | 1 | |
| BC | 14.7 | 25.5 | 21.5 | 20.5 | 3 | |
| BC | 5.6 | 19.0 | 52.3 | 65.9 | 13 | |
| BC | 10.6 | 22.2 | 7.7 | 6.3 | 1 | |
| BC | 1 | 20.0 | 14.7 | 10.7 | 1 | |
| BC | 6.9 | 34.0 | 6.6 | 5.3 | 1 |
将以上所得到的参数值代入式(7),可通过计算得到拱顶下沉和周边收敛总量分别为207.4 mm和193.6 m。由于已产生的各项位移达到各项预计位移总量的80%~90%,拱顶下沉为176.3~186.7 mm,周边收敛达到154.9~174.2 mm,假设隧道掌子面的施工速度为2 m/d,则可推算得到二衬合理支护时间为22 d,并且此时断面与掌子面的距离为68 m。
3 结论(1) 探讨了围岩与衬砌的相互关系,通过理论推导得到了同时考虑时空效应的隧道围岩变形修正计算公式,该公式包含了时间参数,可确定达到不同衬砌位移及围岩位移所需要的时间。
(2) 以某高速公路隧道工程为背景,针对隧道拱顶下沉、周边收敛、围岩压力和初衬内力,开展了隧道二衬合理支护时机的监测分析,得到了围岩变形修正公式中的待定系数,并最终确定隧道衬砌的合理支护时机。
| [1] | 王祥秋, 杨林德, 高文华. 软弱围岩蠕变损伤机理及合理支护时间的反演分析[J]. 岩石力学与工程学报,2004,23 (5) :793–796. WANG Xiang-qiu, YANG Lin-de, GAO Wen-hua. Creep Damage Mechanism and Back Analysis of Optimum Support Time for Soften Rockmass[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23 (5) : 793–796 . |
| [2] | 赵晓勇. TBM法隧道施工下穿涵洞的数值模拟研究[J]. 地下空间与工程学报,2011,7 (3) :513–517. ZHAO Xiao-yong. Study on the TBM Tunnel beneath Existing Culvert by Numerical Simulation[J]. Chinese Joumal of Underground Space and Engineering, 2011, 7 (3) : 513–517 . |
| [3] | 林杭, 李江腾, 曹平. 岩石临界应变能释放率测试及其相关规律[J]. 中南大学学报:自然科学版,2013,44 (2) :714–717. LIN Hang, LI Jiang-teng, CAO Ping. Critical Strain Energy Release Rate Test and Its Interrelated Law of Rock Parameters[J]. Journal of Central South University:Science and Technology Edition, 2013, 44 (2) : 714–717 . |
| [4] | 郭小红, 王梦恕. 隧道支护结构中锚杆的功效分析[J]. 岩土力学,2007,28 (10) :2234–2239. GUO Xiao-hong, WANG Meng-shu. Analysis of Efficacy of Rock Bolt for Tunnel Support Stucture[J]. Rock and Soil Mechanics, 2007, 28 (10) : 2234–2239 . |
| [5] | 刘志春, 李文江, 朱永全, 等. 软岩大变形隧道二次衬砌施作时机探讨[J]. 岩石力学与工程学报,2008,27 (3) :580–588. LIU Zhi-chun, LI Wen-jiang, ZHU Yong-quan, et al. Research on Construction Time of Secondary Lining in Soft Rock of Large-deformation Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (3) : 580–588 . |
| [6] | 张社荣, 梁礼绘. 考虑三维应力旋转的隧洞衬砌支护时机研究[J]. 水利学报,2007,38 (6) :704–709. ZHANG She-rong, LIANG Li-hui. Analysis on Tunnel Liner Supporting Time Considering Three-dimensional Stress Rotation[J]. Journal of Hydraulic Engineering, 2007, 38 (6) : 704–709 . |
| [7] | 荣耀. 巷道支护时机与围岩级别关系的研究[J]. 矿山压力与顶板管理,2003,20 (4) :11–13. RONG Yao. The Study of the Relation of Pudding Time of Tunnel's Country Rock Support and the Class of the Country Rock[J]. Ground Pressure and Strata Control, 2003, 20 (4) : 11–13 . |
| [8] | 辛全山, 刘善永, 赵延峰. 利用二次耦合理论确定二次支护的最佳时间[J]. 山东煤炭科技,2003, (4) :16–17. XIN Quan-shan, LIU Shan-yong, ZHAO Yan-feng. Using Second Coupling Theory to Define the Best Time of Second Support[J]. Shandong Coal Science and Technology, 2003, (4) : 16–17 . |
| [9] | 张鹏, 李宁, 何敏. 软岩圆形隧洞衬砌支护时机现场变形监测判据研究[J]. 西安理工大学学报,2007,23 (2) :140–143. ZHANG Peng, LI Ning, HE Min. Theoretical Estimation of the Supporting Time in Soft Rocks Tunnels under High Initial Stress[J]. Journal of Xi'an University of Technology, 2007, 23 (2) : 140–143 . |
| [10] | SULEM J, PANET M, GUENOT A. Closure Analysis in Deep Tunnels[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1987, 24 (3) : 145–154 . |
| [11] | 欧阳建, 付云升, 石维新, 等. 南水北调中线西四环暗挖段暗涵二衬支护时机的研究[J]. 南水北调与水利科技,2008,6 (1) :48–51. OUYANG Jian, FU Yun-sheng, SHI Wei-xin, et al. Timbering Opportunity of the Buried Culvert under the West Fourth Ring Road of the Middle Route Project in the South-to-North Water Diversion[J]. South-to-North Water Transfers and Water Science & Technology, 2008, 6 (1) : 48–51 . |
| [12] | 张周平, 余伟健, 高谦, 等. 金川深部工程围岩支护时机与参数设计研究[J]. 金属矿山,2008, (2) :40–44. ZHANG Zhou-ping, YU Wei-jian, GAO Qian, et al. Study on Time and Parameter Design for Engineering Support of Wall Rock at Depth in Jinchuan Mine[J]. Metal Mine, 2008, (2) : 40–44 . |
 2016, Vol. 33
2016, Vol. 33
