扩展功能
文章信息
- 毛德均, 钱永久
- MAO De-jun, QIAN Yong-jiu
- 套箍法加固RC轴压柱承载力计算方法研究
- Study on Calculation Methods of Bearing Capacity of RC Axial Compression Column Strengthened with Hoop
- 公路交通科技, 2016, 33(7): 76-85
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(7): 76-85
- 10.3969/j.issn.1002-0268.2016.07.012
-
文章历史
- 收稿日期:2015-09-14
轴心受压构件的极限承载力是受压构件承载力的上限值,在工程设计中常常作为强度复核和初步估算截面的重要手段,具有重要的理论意义[1]。套箍法属于增大截面加固法范畴,目前,在工程加固中已被广泛用于RC墩柱的加固[2-3]。针对加固柱极限承载能力的计算,我国现行GB 50367—2013《混凝土结构加固设计规范》[4](以下简称GB加固规范)和JTG/T J22—2008《公路桥梁加固设计规范》[5](以下简称JTG加固规范)都给出了各自的方法。此外,一些研究者也给出了不同的方法[3, 6-9],从中可以发现,对加固柱极限承载能力计算方法的研究,人们关注的重点多为如何合理准确地计算出新增部分的承载贡献程度。对于套箍层对原柱(也可称核心柱,本文不进行区分)混凝土的约束增强效应,上述两种规范方法和部分研究者[6-7]给出的方法没有考虑,但也有研究者[8-9]给出了考虑套箍约束增强效应的承载力计算公式。
对适用于同一对象的不同计算方法进行探讨是一些研究者关注的重点[10-11]。就套箍法加固RC轴压柱的极限承载力计算而言,GB加固规范、JTG加固规范和不同研究者给出的方法在形式上存在差异,计算表明得到的结果也相差较大。因此,比较各种计算方法的精度并探讨其可能存在的问题是必要的,但目前未见相关研究成果的文献报道。本文通过对算例和搜集到的有关试件进行计算分析,同时结合一定理论分析,重点讨论了GB加固规范、JTG加固规范和文献[7-8]中给出的4种不同计算方法,对这几种典型计算方法的适用性进行了研究。在此基础上,还提出了一种计算套箍法加固RC轴压柱的实用计算方法,并应用有限元分析结果和现有试验研究成果,对提出公式进行了验证。
1 4种不同计算方法对比分析 1.1 公式简介 1.1.1 GB加固规范按照GB加固规范第5.4.1节规定,套箍法加固RC轴心受压构件的正截面承载力计算公式为:

|
(1) |
式中,N为构件加固后的轴向压力设计值;φ为构件稳定系数;fc,fc0分别为新、旧混凝土轴心抗压强度设计值;Ac0,Ac分别为构件加固前混凝土截面面积和加固后新增部分混凝土截面面积;f′y,f′y0分别为新增纵向钢筋和原纵向钢筋的抗压强度设计值;A′s,A′s0分别为新增纵向钢筋和原纵向钢筋的截面面积;αcs为综合考虑新增混凝土和钢筋强度利用程度的降低系数(以下简称强度折减系数),取值为0.8。各材料强度设计取值按现行《混凝土结构设计规范》确定。
GB加固规范考虑了二次受力过程中由于新增部分的应力应变滞后,导致其强度得不到有效发挥的影响,故在进行截面承载力计算时,对新增部分统一乘以强度折减系数αcs=0.8。
1.1.2 JTG加固规范JTG加固规范第5.3.1节给出的承载力计算公式为:
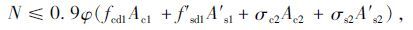
|
(2) |
式中,φ意义同前;fcd1,f′sd1分别为原构件混凝土轴心抗压强度设计值和纵向钢筋抗压强度设计值;Ac1,Ac2分别为原构件和新增部分混凝土截面面积;A′s1,A′s2分别为原有纵向普通钢筋和新增纵向普通钢筋的截面面积;σc2为在达到承载能力极限状态时,新增混凝土的应力,σc2=Ec2εc2≤fcd1;σs2为在达到承载能力极限状态时,新增纵向钢筋的应力,σs2=Es2εs2≤f′sd2,f′sd2为新增纵向钢筋的抗压强度设计值,各材料强度设计取值按现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》确定;εc2为新增混凝土的应变;εs2为新增钢筋的应变,计算公式为:

|
(3) |
式中,εcu为轴心受压混凝土极限压应变,取值εcu=0.002;Ec1,Es2分别为原构件混凝土弹性模量和新增纵向受压钢筋的弹性模量;αEs为原构件纵向普通钢筋与混凝土弹性模量比,αEs=Es1/Ec1;b1,h1为原构件截面宽度与高度;Nd1为第一阶段轴向力组合设计值。
JTG加固规范先根据构件加固前在荷载作用下的实际应变和加固后构件达到承载能力极限状态时混凝土的极限压应变,按平截面假定确定新增钢筋和混凝土在构件破坏时的应变εs2,εc2,再根据弹性理论的应力等于弹性模量乘以应变确定新增钢筋和混凝土的应力值,且分别小于新增钢筋和旧混凝土的抗压强度设计值,进而确定加固构件的极限承载力。显然,同样是考虑加固柱的二次受力特性,JTG加固规范的两阶段计算法和GB加固规范的折减系数法区别明显。
1.1.3 两种公开文献报道的计算方法罗苓隆在文献[7]中给出的计算公式为:

|
(4) |
式中,α为新增钢筋和混凝土的强度折减系数,计算式见式(7);其余符号意义同式(1)。
式(4)在形式上与式(1)一致,前者与后者的主要区别为:考虑加固柱的二次受力特性,新增部分的强度折减系数取值不是固定值0.8,而是用与核心柱混凝土初始应力水平β有关的函数式α=2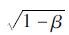
程昌熟在文献[8]中给出的计算公式为:
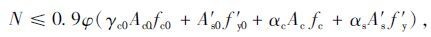
|
(5) |
式中,γc0为原柱旧混凝土的强度提高系数,计算式见式(18);αc为新增混凝土强度折减系数,计算式同式(4)中的α;αs为新增钢筋强度折减系数,计算式见式(8);其余符号意义同式(1)。
式(5)与式(4)的主要区别为:用强度提高系数来计入新增套箍层对原柱混凝土的约束增强影响;新增混凝土和钢筋的强度折减系数分开计算,其中钢筋的强度折减系由β和钢筋材料特性共同决定。
显然,GB加固规范的计算原理和JTG加固规范相通,实现途径有所区别,后者的计算过程比前者相对复杂;而罗和程给出的计算方法可视为是对GB加固规范方法的改进,计算过程和JTG加固规范相当。
1.2 算例配筋对比分析算例1[12]:某RC轴心受压柱截面尺寸为400 mm×400 mm,混凝土等级为C20,原柱配有4-20受压钢筋,箍筋按构造配筋,柱计算长度为7.2 m。由于某种原因导致荷载增加,增加后柱的轴向力设计值为3 800 kN。根据验算该柱强度不满足要求,需要进行加固,采用钢筋混凝土套箍法进行加固。加固时原柱所受轴向力设计值为1 320 kN,加固用混凝土为C30,套箍层厚度定为100 mm,加固用钢筋等级为Ⅱ级HRB335钢筋,确定加固纵向受力钢筋用量。
将由4个公式计算求得的配筋量列于表 1。
由表 1可知,不同方法得出的配筋量存在明显差异。其中文献[7]罗的配筋量最大,GB加固规范最小,前者是后者的2.56倍;从已省略的计算过程可知,罗的新增部分强度折减系数计算值为0.674,小于规范的取值0.8,强度折减系数减小导致计算承载能力相对降低通过增大配筋量来弥补。
文献[8]程的配筋量是GB加固规范的1.21倍。程的计算方法考虑了套箍层对核心柱混凝土强度的约束提高,强度提高系数计算值为1.244,而新增混凝土和钢筋的强度折减系数分别为0.674和0.572,均小于规范取值0.8;和GB加固规范相比,核心柱混凝土强度提高导致承载能力提升和新增部分承载贡献减小综合作用使得配筋量略有增加。
JTG加固规范的配筋量是GB加固规范的2.42倍。就直接指导工程加固设计的规范方法而言,GB加固规范和JTG加固规范,由于在不同的工程结构中,构件所处的工作环境、承受荷载的性质、使用特点不同,采用的可靠度指标不同。其中GB加固规范的混凝土材料分项系数取值为1.4,钢筋的材料分项系数取值为1.1;而JTG加固规范的混凝土材料分项系数取值为1.45,钢筋的材料分项系数取值为1.2,由此导致二者得出的配筋量存在差异不难理解。但是,将JTG加固规范的材料强度值代入GB加固规范的公式进行配筋求解,得到的配筋量为A′s=2 036 mm2,即此时新增纵筋的配筋量也是GB加固规范的1.62倍。可见,造成JTG加固规范配筋量与GB加固规范存在明显差异的主要原因是其本身的计算方法。
综上可知,各种方法的计算结果差异明显。对新增部分的强度利用程度如何界定取值,以及是否考虑套箍层对原柱混凝土的约束增强作用对公式结果有明显影响。
1.3 计算值与实测值对比分析结合现有试验资料对各公式的适用性进行计算分析。将查阅大量文献搜集到可用于计算分析的12根试验柱参数资料列于表 2。由表 2可知,现有试验研究的试件总量还偏少,试件变化参数主要为核心柱的初始应力水平指标β′,β′的取值范围主要集中在0~0.60内,且规律性较差,有必要有针对性地补充相关试验。
| 试件编号 | 数据来源 | Ac0/mm2 | A/mm2 | A′s0/mm2 | A′s/mm2 | fcu1/MPa | fcu2/MPa | β′ | N1/kN | f′y/MPa | f′y0/MPa | Es/GPa | Es0/GPa | l0/cm |
| HZA-1 | [6] | 200×206 | 302×303 | 314 | 628 | 31.8 | 30.7 | 0 | 0 | 284 | /354 | 209 | 189 | 140 |
| HZA-2 | [6] | 193×201 | 299×305 | 314 | 628 | 31.8 | 26.2 | 0.31 | 321 | 284 | /354 | 209 | 189 | 140 |
| HZA-3 | [6] | 199×203 | 300×303 | 314 | 628 | 31.8 | 25.4 | 0.65 | 702 | 284 | /354 | 209 | 189 | 140 |
| HZA-4 | [6] | 199×201 | 296×303 | 314 | 628 | 31.8 | 23.8 | 0.78 | 843 | 284 | /354 | 209 | 189 | 140 |
| A-1 | [13] | 150×149 | 251×248 | 314 | 415 | 26.2 | 10.4 | 0.48 | 237 | 331 | /331 | 200 | 200 | 180 |
| A-2 | [13] | 149×149 | 250×248 | 314 | 415 | 26.2 | 10.4 | 0.58 | 285 | 331 | /331 | 200 | 200 | 180 |
| A-3 | [13] | 150×151 | 251×251 | 314 | 415 | 26.2 | 29.4 | 0.55 | 275 | 331 | /331 | 200 | 200 | 180 |
| A-4 | [13] | 150×149 | 251×250 | 314 | 415 | 26.2 | 29.4 | 0.61 | 301 | 331 | /331 | 200 | 200 | 180 |
| YJGZ | [3] | 200×200 | 299×302 | 452 | 452 | 30.3 | 61.8 | 0 | 0 | 367 | /367 | 210 | 210 | 190 |
| JGZ-1 | [3] | 200×200 | 299×302 | 452 | 452 | 30.3 | 52.6 | 0.22 | 204 | 367 | /367 | 210 | 210 | 190 |
| JGZ-2 | [3] | 200×200 | 300×301 | 452 | 452 | 30.3 | 61.8 | 0.39 | 360 | 367 | /367 | 210 | 210 | 190 |
| JGZ-3 | [3] | 200×200 | 299×303 | 452 | 452 | 30.3 | 52.6 | 0.50 | 460 | 367 | /367 | 210 | 210 | 190 |
| 注:A为加固后柱截面面积;fcu1,fcu2分别为原柱混凝土和新增混凝土的立方体抗压强度;β′=N1/Nu为加固前核心柱受到的轴向力与其极限承载力计算值的比值,即核心柱的初始应力水平指标;Es,Es0分别为新、旧钢筋弹性模量;l0为加固柱的计算长度;其余符号意义同式(1)。公式计算所用的材料强度值,按《混凝土结构试验方法标准》(GBT0152—2012)的方法推定得到。 | ||||||||||||||
4种计算方法得到的试件承载能力计算值和试验得到的实测值数据见表 3,计算值与实测值有关的统计分析结果见表 4。
| 试件编号 | Nu,G/kN | Nu,J/kN | 罗苓隆计算值/kN | 程昌熟计算值/kN | 实测值Nu/kN | Nu,G/Nu | Nu,J/Nu | 计算值/实测值 | |
| 罗苓隆 | 程昌熟 | ||||||||
| HZA-1 | 1 969 | 2 596 | 2 212 | 2 571 | 2 150 | 0.916 | 1.207 | 1.029 | 1.160 |
| HZA-2 | 1 824 | 2 604 | 2 009 | 2 275 | 2 264 | 0.806 | 1.150 | 0.887 | 0.990 |
| HZA-3 | 1 810 | 2 585 | 1 813 | 2 046 | 2 107 | 0.859 | 1.227 | 0.860 | 0.971 |
| HZA-4 | 1 746 | 2 550 | 1 594 | 1 800 | 1 911 | 0.914 | 1.334 | 0.834 | 0.942 |
| A-1 | 820 | 1 558 | 8 68 | 919 | 1 181 | 0.694 | 1.319 | 0.735 | 0.778 |
| A-2 | 817 | 1 553 | 845 | 890 | 1 153 | 0.709 | 1.347 | 0.733 | 0.772 |
| A-3 | 1 248 | 1 575 | 1 329 | 1 473 | 1 851 | 0.674 | 0.851 | 0.718 | 0.796 |
| A-4 | 1 243 | 1 570 | 1 292 | 1 430 | 1 803 | 0.689 | 0.871 | 0.717 | 0.793 |
| YJGZ | 2 799 | 2 499 | 3 254 | 4 015 | 4 367 | 0.641 | 0.572 | 0.745 | 0.914 |
| JGZ-1 | 2 545 | 2 499 | 2 914 | 3 548 | 3 872 | 0.657 | 0.645 | 0.753 | 0.916 |
| JGZ-2 | 2 799 | 2 497 | 3 159 | 3 892 | 4 155 | 0.674 | 0.601 | 0.760 | 0.937 |
| JGZ-3 | 2 554 | 2 498 | 2 804 | 3 420 | 3 730 | 0.685 | 0.670 | 0.752 | 0.917 |
| 注:Nu,G为GB加固规范方法的计算值;Nu,J为JTG加固规范方法的计算值。 | |||||||||
JTG加固规范计算值和实测值比值的均值为0.983,不安全的柱子数量为6根,所占比例高达50%,不安全柱计算值与实测值的最大偏差为34.7%,综合表明JTG加固规范结果偏于不安全。GB加固规范的计算值均小于实测值,最大偏差为35.9%也不够合理,计算与实测比值的均值为0.743,表明GB加固规范结果整体偏于安全。对于HZA-4号试件,GB加固规范的计算与实测比值为0.914,该试件的初始应力水平为0.78,在所有试件中处于较高水平,这在某种程度上可反映出当原柱的初始应力水平较高时,GB加固规范结果的安全储备可能不足,对此还有待进一步试验验证。计算值和实测值的统计分析结果还表明,JTG加固规范的计算值离散性更大,和实测值的吻合程度也比GB加固规范差。可见,两种规范方法相比,GB加固规范的方法要优于JTG加固规范。
罗苓隆和程昌熟的方法得到的不安全柱数量均为1根,占总数的比例为8.3%,不安全柱的编号均为HZA-1,对于该试件,所有方法的计算值与实测值比值均偏大,因此不排除该试件有一定的初始缺陷,导致其实测承载能力有所降低。罗和程的计算值和实测值比值的均值分别为0.794和0.907,可见,程的计算结果有较适宜的安全储备。罗和程的计算值与实测值有关的统计数据均和GB加固规范方法接近甚至略为更优。二者作为GB加固规范方法的改进,新增部分强度折减系数的计算取值考虑了核心柱的初始应力水平这一重要影响因素,计算结果也更加理想。其中,程的方法在分开考虑新增混凝土和钢筋强度折减系数的同时,还考虑了原柱混凝土强度在套箍层约束作用下的提高,其计算结果也最为理想。从罗和程的结果对比还可以发现,若只考虑由于二次受力导致新增部分强度得不到有效发挥,不考虑新增部分对原混凝土强度的约束提高,将在一定程度上导致承载能力计算结果更偏安全。
从表 1的算例配筋结果可知,JTG加固规范的配筋量是GB加固规范的2.42倍,而基于表 3试验结果的比较又不难发现JTG加固规范结果偏于不安全,前后存在矛盾。原因是JTG加固规范和GB加固规范的计算方法本身存在明显差异,当用二者进行配筋设计时,钢筋和混凝土材料强度取值均为各自规定的设计值,对此两个版本规范间存在差异。而对试验构件的承载力实测值进行复核时,材料强度取值皆为实测值,二者不存在区别。实际工程中,当需要对公式计算结果进行检验时,我们采用的有关参数取值应该是实测值,而不是设计值。因此,配筋设计得出的配筋量并不能真正反映公式计算结果的安全情况。就JTG加固规范和GB加固规范而言,前者是针对桥梁结构加固,后者主要适用房屋建筑结构加固,但作为国家标准规范,其加固设计基本原理适用于土木工程各行业。二者配筋设计结果与实测值复核结果表现矛盾,这反映出二者结果的整体一致性还不够好,应引起关注。
2 实用计算方法分析 2.1 JTG加固规范方法的进一步分析为进一步研究JTG加固规范的计算方法,再利用算例1进行计算分析,其中除原柱的初始应力水平β′变化外,其余参数均不变。根据《公路钢筋混凝土及预应力混凝土桥梁桥涵设计规范》(JTG D62—2004)5.3.1条,原柱的极限承载力为:
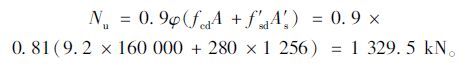
|
对不同β′对应的εc2,εs2,σc2,σs2进行计算,求得数据见表 5。
| β′ | N1/kN | εc2,εs2 | σc2/MPa | σs2/MPa |
| 0 | 0 | 0.002 | 60.0 | 400.0 |
| 0.10 | 132.95 | 0.001 97 | 59.1 | 393.9 |
| 0.20 | 265.90 | 0.001 94 | 58.2 | 387.7 |
| 0.30 | 398.85 | 0.001 91 | 57.2 | 381.6 |
| 0.40 | 531.80 | 0.001 88 | 56.3 | 375.4 |
| 0.50 | 664.75 | 0.001 85 | 55.4 | 369.3 |
| 0.60 | 797.70 | 0.001 82 | 54.5 | 363.2 |
| 0.70 | 930.65 | 0.001 79 | 53.6 | 357.0 |
| 0.80 | 1 063.60 | 0.001 75 | 52.6 | 350.9 |
| 0.90 | 1 196.55 | 0.001 72 | 51.7 | 344.7 |
| 1.00 | 1 329.50 | 0.001 69 | 50.8 | 338.6 |
从表 5可知,随着核心柱初始应力水平β′的提高,新增混凝土和钢筋的应变、应力值都在降低,但不管在何种应力水平下,最后得出的新增部分应力值始终没有小于控制值fcd1=9.2 MPa和f′sd2=280 MPa,用于公式(2)进行计算的σc2和σs2最终还是取用fcd1=9.2 MPa和f′sd2=280 MPa,这就使得εc2和εs2的计算没有实际意义,进而造成整个计算过程失去了考虑两阶段受力进行加固计算的意义,公式(2)可直接写为:

|
(6) |
对比式(6)和式(1)不难发现,JTG加固规范对新增部分的强度处理,实质上是新增钢筋的强度全部得到了发挥,新增混凝土的强度则得不到有效发挥,以旧混凝土强度进行设计控制,εc2,εs2的计算并没有反映出新、旧材料分阶段受力特点,显得繁琐而无用,反而造成公式计算结果不安全。因此,JTG加固规范中εc2,εs2的计算方法在今后规范修订时应进行合理修正。
2.2 新增部分强度折减系数分析本文重点讨论的4种计算方法中,除JTG加固规范以外,其余3种方法都是采用对套箍层新增部分材料乘以强度折减系数来考虑加固柱的二次受力特性影响。
GB加固规范给出的新增混凝土和钢筋的强度折减系数均为αcs=0.8,该取值是在编制我国第一版结构加固规范即CECS25—1990《混凝土结构加固技术规范》时依据当时的试验结果确定的,并一直延用至今。这样处理使得公式计算过程简便许多,但规范条文说明对该取值的解释说明过于笼统,导致在实际加固工程中,工程师往往不能对加固柱给出较为准确的安全度量。故又在GB加固规范条文说明的5.4.1条中注明:当有充分试验依据时,αcs的取值可作适当调整。
罗苓隆[7]给出的新增部分强度折减系数α计算表达式为:

|
(7) |
式中,β为核心柱混凝土的初始应力水平,β=N1/[A′×fc0];A′为核心柱的换算截面积;其余符号意义同式(1)。
程昌熟[8]给出的新增混凝土的强度折减系数αc计算式同式(7),新增钢筋强度折减系数αs的计算式为:
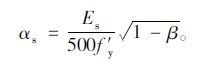
|
(8) |
式中Es为新增钢筋弹性模量,其余符号意义同式(1);当计算出αs>1.0时,说明钢筋已进入塑性区,其取值为1.0。
此外,苏三庆[9]给出的新增混凝土强度折减系数αc计算式也同式(7)。新增钢筋的强度折减系数计算式为:

|
(9) |
对比分析可以发现,给出上述3式的研究者在建立公式时采用的理论分析方法相同,得出的新增混凝土强度折减系数计算方法也相同。对于新增钢筋的强度折减系数,罗为便于计算进行了简化,直接取为和混凝土相同的计算方法,而程和苏是将两种材料的强度折减系数分开计算。由于混凝土和钢筋的材料特性并不一样,二者的强度折减系数也必定不等,因此,分开计算是必要而合理的。
程和苏的不同之处在于后者最后对新增钢筋的折减系数计算也进行了简化处理,其根据钢筋的弹塑性本构关系,用新增钢筋弹性模量乘以混凝土的轴压极限压应变0.002来近似等于新增钢筋的抗压强度设计值,从而得出了式(9)。这种做法不够合理,因为对于常用的Ⅰ级、Ⅱ级和Ⅲ级钢筋,钢筋弹性模量乘以应变值0.002得出的值都大于钢筋本身的抗压强度设计值,这就导致在进行加固设计时得出的钢筋强度折减系数往往低于实际值,造成误差且违背了计算基本前提,而程没有进行简化,得出了式(8)。比较上述3种折减系数计算方法,显然是没有作任何简化的程的方法更合理,可供工程加固实践参考。
康光宗[14]等通过理论分析,给出的新增部分强度折减系数α的计算表达式为:

|
(10) |
式中,ΔN1为原柱加固前的卸载量;αEs意义同式(3);ρs1为原柱配筋率;其余符号意义同式(1)。
式(10)涵盖了多个影响参数,看似更加合理,但进一步分析便可发现,由于ΔN1/[(1+αEsρs1)Ac0]=Δσc1,则α=Δσc1/fc0,即新增部分的强度折减系数α等于原柱混凝土的应力水平降幅Δβ;若加固前原柱的卸载量ΔN1=0,则得出的α=0,即此时新增部分完全不发挥作用,这明显不合理。实际加固时,即使原柱应力水平已达到较高水平,也必然存在由于一些条件限制而无法卸载的情形,且当一阶段受力程度未超出一定限值时也可以不进行卸载。从试验验证方面看,在进行加固柱的静力破坏试验时,对二阶段受力的加载、部分卸载、加固后再加载直至破坏这一过程的模拟非常困难,目前也尚无相关资料可查,式(10)的适用性很难得到验证。因此,虽然文献[14]对折减系数的计算作了有益探讨,但参考价值有限。
盛光复[15]也给出了两种模式下新增加固部分强度折减系数α的计算表达式。
模式1:当新增混凝土在加固柱达到承载能力极限时的应变小于新增钢筋抗压极限应变,即(εc0-

|
(11) |
模式2:当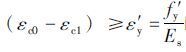

|
(12) |
式(11)、(12)中,ρ′s为新增截面纵筋相对于新增截面的配筋率;εc1为原构件加固前混凝土的初始应变;εc0为轴心受压混凝上的极限压应变,取值εc0=0.002;α′E为新增钢筋和混凝土的弹性模量比;其余符号意义同式(1)。对式(11)和(12)作变换后进行分析。
加固前原柱混凝土的应力水平指标:

|
(13) |
加固前原柱混凝土的应变水平指标:

|
(14) |
由混凝土的本构关系曲线可以推知

|
(15) |
则公式(11)可变换为:

|
(16) |
公式(12)可变换为:

|
(17) |
对比式(7)和式(16)、(17),可以认为盛光复的计算方法是对式(4)的进一步改进,涵盖了更多的影响参数。显然,用盛光复的方法进行计算比较麻烦,尤其是进行配筋计算时,由于事先不确定新增截面的配筋率,故不能确定折减系数α,α不确定又将导致配筋计算无法进行,这就需要多次试算来进行求解,导致计算过程复杂,不利于工程师掌握和公式的推广应用。目前,式(16)和(17)也尚无试验资料可供验证。
对于新增部分的强度折减系数,在没有更多试验资料支撑的前提下,目前很难提出其他有效计算方法。不难发现,不同研究者提出的折减系数计算方法和JTG加固规范的方法都涉及到了原柱一阶段的受力水平这一重要指标。但在实际工程中,要比较准确地估算一阶段的受力情况很难做到,而且对实际荷载的估算往往因人而异,这也正是这些计算方法存在的局限性。
2.3 套箍约束增强效应分析对于套箍层对原柱混凝土的约束增强效应,在建立加固柱承载能力计算方法时,显然有如下两种选择:
(1) 不考虑,即忽略加固后套箍层对原柱混凝土抗压强度的约束提高;
(2) 考虑,采用近似方法对核心柱混凝土的增强系数进行计算。
本文讨论的两种规范方法都没有考虑。查阅的相关文献中,只有文献[8]程和文献[9]苏给出的计算方法做了考虑,二者给出的约束效应对原柱混凝土的强度提高系数计算式均为:

|
(18) |
式中,t为套箍加固层厚度;d为矩形短边长度;阴影部分为有效约束面积如图 1所示;其余符号意义同式(1)。

|
| 图 1 有效约束面积 Fig. 1 Effective restraint areas |
| |
式(18)是根据套箍法加固RC圆柱的理论推导公式乘以折减系数0.8得到。折减系数取值0.8缺乏理论和试验依据。且不难发现,对于长宽比等于1的正方形截面,方法用于近似计算偏差不会太大,但是在加固设计中进行强度复核和截面初步估算时,对于长宽比不等于1的矩形截面,该方法得到的圆形有效约束面积与核心柱截面积比值,将随矩形长宽比的增大而减小,导致用于计算的约束混凝土面积比实际面积大;而且混凝土圆柱受到的套箍约束是均匀受压[1, 9],方柱比圆柱的约束受力机理更为复杂,原柱混凝土不再受均匀的约束力,截面不同位置处套箍层混凝土的应变也不再一致。因此,公式(18)的适用性并不会太好。Takeuti[16]认为,虽然矩形柱和圆形柱一样,存在套箍层对核心柱的约束效应,但是约束效果远不及圆形柱明显,也很难运用现有约束混凝土强度模型来做比较准确的计算。
根据加固柱的二次受力特点,可以分析出套箍层对核心柱混凝土约束增强原理为:考虑套箍层混凝土的抗拉强度,不考虑普通箍筋约束作用,加固柱二次受力后,核心柱混凝土产生的累积横向膨胀变形大于套箍层混凝土,导致套箍层混凝土受拉,在核心柱截面四边的直线段,由于RC套箍层具有一定的刚度而不易产生水平弯曲,从而对核心柱混凝土产生一定的约束;在核心柱截面转角处,两个互相垂直方向上的套箍层混凝土拉力又形成沿原柱对角线方向上的合力,该合力在原柱对角线方向又形成约束,总的约束效应是上述两部分的叠加,套箍层混凝土纵向开裂后,约束作用消失。
同样是套箍形式加固,外包钢形成矩形钢管混凝土加固和CFRP环向围束加固矩形柱的研究成果可以借鉴到RC套箍加固矩形柱的分析上。有研究表明,矩形钢管混凝土中,方钢管对管内混凝土的套箍效应相对较弱,约束增强作用有限,通常不作考虑[17]。对于CFRP环向围束加固矩形柱,倒角半径大小和矩形截面的长宽比都对柱截面的约束应力分布和约束效果有重要影响。当前,不同研究者提出的CFRP约束矩形柱计算模型的适用性也并不够理想[18-19],而混凝土材料的离散性比钢材和CFRP大。
综上所述,一方面,要对套箍加固柱的极限承载力作更精准的计算,考虑套箍约束增强效应无疑是必要的;另一方面,套箍加固矩形截面的约束受力复杂,混凝土材料的离散性也较大,要建立比较符合实际的模型来计算约束增强效应已相当困难。而且如果只考虑核心柱混凝土强度的约束增强,忽略套箍层混凝土的强度降低也不尽合理,但要做到二者兼顾难度更大。从前面的计算分析结果可知,不考虑约束作用的结果是得出的承载能力计算值偏于安全。因此,计算时可以不考虑套箍层对核心柱混凝土的约束增强效应,将其用作安全储备。
2.4 本文提出的计算方法 2.4.1 思路及公式有国外研究者就认为,套箍层的混凝土保护层对加固柱的极限承载力贡献有限[16]。而文献[3, 20]中对加固柱破坏过程及现象的有关论述也表明:在加载过程中,套箍层的混凝土保护层在柱子达到极限承载力前就已经发生开裂、剥落破坏,而在加固柱达到极限承载力时,套箍层中的新增钢筋能达到屈服。结合前面的分析,基于以下思路,本文提出了一种计算加固柱极限承载能力的实用计算方法:
(1) 不考虑套箍层的混凝土保护层对加固柱的极限承载贡献,其余新增混凝土的强度全部得到发挥;
(2) 新增纵向钢筋强度全部得到发挥;
(3) 不考虑套箍层对核心柱的约束作用,用于安全储备;
(4) 核心柱的钢筋和混凝土强度全部得到有效发挥;
(5) 构件稳定系数及可靠度系数的计算取值和GB加固规范相同。
综上几点,得出如下公式:

|
(19) |
式中,Ac,inner为扣除混凝土保护层厚度后的新增部分混凝土截面面积;其余符号意义同式(1)。
公式(19)在计算时不需要对原柱的一阶段受力情况进行估算,应用方便。下面结合有限元计算结果和表 2试件的试验结果对其可用性进行验证。
2.4.2 有限元分析模型简介用有限元分析软件ANSYS对表 2中的试件进行数值计算分析。试验柱的混凝土用SOLID65单元模拟,钢筋用LINK8单元模拟,用SOLID45单元模拟加载过程中防止柱端部发生局部破坏的钢垫板。钢筋和混凝土的本构关系采用GB 50010—2010《混凝土结构设计规范》[21]中提供的模型。建模时,试件的材料特性采用各参考文献中给出的实测值,模型柱的构造尺寸等取值也与试验一致。
相关试验研究结果表明,钢筋和混凝土之间以及套箍层和原柱混凝土结合面的黏结状况良好[3, 6, 13, 22-23]。因此,模型不考虑钢筋和混凝土之间以及新老混凝土之间的黏结滑移问题。利用ANSYS求解模块中的单元生死(Birth and Death)命令来控制套箍新增部分是否参与工作,从而模拟加固柱的二次受力问题。在第一阶段,先将套箍新增部分单元杀死,模拟原柱加固前的受力状况;第二阶段,再将套箍新增部分单元激活,模拟加固后柱的二次受力过程。
在柱顶相应单元上施加面荷载,采用牛顿-拉普森迭代法求解,收敛容差釆用ANSYS默认值,取荷载-位移曲线的峰值点作为极限承载力。
2.4.3 公式验证对于表 2中的试件资料,式(19)的计算值、有限元计算值与试验实测值的有关数据见表 6。
| 试件编号 | 公式计算值/kN | 有限元计算值/kN | 实测值/kN | 计算值/实测值 | |
| 式(19) | 有限元 | ||||
| HZA-1 | 1 937 | 2 110 | 2 150 | 0.901 | 0.981 |
| HZA-2 | 1 815 | 2 100 | 2 264 | 0.802 | 0.928 |
| HZA-3 | 1 801 | 1 970 | 2 107 | 0.855 | 0.935 |
| HZA-4 | 1 756 | 1 786 | 1 911 | 0.919 | 0.935 |
| A-1 | 835 | 1 076 | 1 181 | 0.707 | 0.911 |
| A-2 | 833 | 1 049 | 1 153 | 0.723 | 0.910 |
| A-3 | 1 231 | 1 723 | 1 851 | 0.665 | 0.931 |
| A-4 | 1 232 | 1 680 | 1 803 | 0.683 | 0.932 |
| YJGZ | 2 751 | 4 070 | 4 367 | 0.630 | 0.932 |
| JGZ-1 | 2 509 | 3 680 | 3 872 | 0.648 | 0.950 |
| JGZ-2 | 2 751 | 4 011 | 4 155 | 0.662 | 0.965 |
| JGZ-3 | 2 509 | 3 619 | 3 730 | 0.673 | 0.970 |
由表 6可知,有限元计算值和实测值非常接近,偏差在10%以内,表明有限元分析具有足够的精度,可用于参数分析,同时也反映出用这些试验结果来进行公式验证和本文有限元模型的相关处理方法均是可行的。对于所有试件,式(19)的计算值均小于实测值,表明计算结果是安全的。
对式(19)的计算值和实测值进行统计分析,有关结果见表 7,表 7的符号意义同表 4。
| 计算方法 | m | D | CV | r |
| 式(19) | 0.739 | 0.010 6 | 0.139 1 | 0.957 6 |
由表 7可知,式(19)的计算结果偏于安全,结合表 3和表 4可知,式(19)与GB加固规范方法的计算效果相近。可见,式(19)具有一定的可用性,可为相关人员提供参考。
3 结论(1) 现行JTG加固规范的计算方法适用性较差,原因是其一阶段受力后原柱应变计算存在问题,使得二阶段受力后新增部分的应变计算值偏高,导致最后得出的承载能力计算结果偏不安全,应引起关注。
(2) GB加固规范的计算结果整体偏于安全。当用折减系数来计入新增部分强度不能有效发挥的影响时,新增材料的折减系数和初始应力水平等因素有关,两种材料的强度折减系数也并不相等。在结构加固中,当可以比较精确地估算出加固前原柱的初始应力水平时,新增混凝土和钢筋的强度折减系数可分别采用文中的式(7)和(8)来进行计算。
(3) 对于矩形加固柱的套箍层对核心柱混凝土的约束增强效应,可以不予考虑,用作安全储备。
(4) 本文提出了一种计算套箍法加固RC轴压柱极限承载力的简便方法,公式计算结果偏于安全,可为工程加固提供一定参考。
| [1] | 郑继光. 二次受力叠合式钢筋混凝土圆截面柱受压性能分析及承载力研究 [D]. 长春:吉林大学,2011. ZHENG Ji-guang. Analysis on Compression Performance of RC Composite Circular Column Subjected to Secondary Load and Study on Its Bearing Capacity [D]. Changchun: Jilin University, 2011. |
| [2] | JÚLIO E S, BRANCO F, SILVA V D. Structural Rehabilitation of Columns with Reinforced Concrete Jacketing[J]. Progress in Structural Engineering & Materials, 2003, 5 (1) : 29–37 . |
| [3] | 何红霞. 自密实混凝土增大截面法加固轴心受压柱的研究与应用 [D]. 长沙:中南大学,2007. HE Hong-xia. Research and Application of Axial Compression Columns Strengthened by Enlarge Section Method with Self-compacting Concrete [D]. Changsha: Central South University, 2007. |
| [4] | GB 50367-2013,混凝土结构加固设计规范 [S]. GB 50367-2013, Code for Design of Strengthening Concrete Structure [S]. |
| [5] | JTG/TJ22-2008,公路桥梁加固设计规范 [S]. JTG/TJ22-2008, Specifications for Strengthening Design of Highway Bridge [S]. |
| [6] | 韩兵康. 钢筋混凝土柱加大截面加固的试验研究 [D]. 上海:同济大学,1993. HAN Bing-kang. Experimental Research on Reinforced Concrete Columns Strengthened by Enlarge Section Method [D]. Shanghai: Tongji University, 1993. |
| [7] | 罗苓隆. 加大截面加固钢筋混凝土构件的正截面强度计算方法[J]. 四川建筑科学研究,1989, (4) :17–20. LUO Ling-long. Calculation Method of Normal Section Bearing Capacity for Reinforced Concrete Member Strengthened by Enlarge Section Method[J]. Sichuan Building Science, 1989, (4) : 17–20 . |
| [8] | 程昌熟. 外包钢筋混凝土加固柱正截面承载力理论分析 [D]. 长沙:湖南大学,2003. CHENG Chang-shu. Theoretical Analysis of Normal Section Strength of Column Reinforced with Enclosed Reinforced Concrete [D]. Changsha: Hunan University, 2003. |
| [9] | 苏三庆, 丰定国, 王清敏. 用外包钢筋混凝土方法加固 RC 轴心受压柱的承载力计算[J]. 西安建筑科技大学学报:自然科学版,1997,29 (4) :29–33. SU San-qing, FENG Ding-guo, WANG Qing-min. Calculation of Load Carrying Capacity of Axially Compressive RC Columns Strengthened with Enclosed Reinforced Concrete[J]. Journal of Xi'an University of Architecture & Technology:Natural Science Edition, 1997, 29 (4) : 29–33 . |
| [10] | 林上顺, 陈宝春. 钢筋混凝土偏压构件承载力各国规范算法比较[J]. 广西大学学报:自然科学版,2014,39 (1) :88–94. LIN Shang-shun, CHEN Bao-chun. Comparison on Calculation Methods for Load Bearing Capacity of Reinforced Concrete Members in codes of Various Countries[J]. Journal of Guangxi University: Natural Science Edition, 2014, 39 (1) : 88–94 . |
| [11] | 陈宝春, 林上顺. 混凝土偏压柱承载力计算方法[J]. 交通运输工程学报,2014,14 (1) :18–25. CHEN Bao-chun, LIN Shang-shun. Calculation Methods of Bearing Capacities of Eccentrically Loaded Concrete Columns[J]. Journal of Traffic and Transportation Engineering, 2014, 14 (1) : 18–25 . |
| [12] | 赵考重, 王莉, 贾留东. 钢筋砼受压构件加固计算[J]. 山东建筑工程学院学报,1995,10 (4) :25–30. ZHAO Kao-chong, WANG Li, JIA Liu-dong. Consolidation Calculation of Reinforced Concrete Members in Compression[J]. Journal of Shandong Institute of Architecture and Engineering, 1995, 10 (4) : 25–30 . |
| [13] | 季强, 苏三庆, 张心斌. 用外包钢筋混凝土法加固RC柱性能的试验研究[J]. 工业建筑,2005,35 (S1) :945–947. JI Qiang, SU San-qing, ZHANG Xin-bin. An An Experimental Study on Behavior of RC Columns Strengthened with Enclosed Reinforced Concrete[J]. Industrial Construction, 2005, 35 (S1) : 945–947 . |
| [14] | 康光宗, 戚跃然, 刘军. 对钢筋混凝土轴心受压柱增大截面加固中强度折减系数取值的进一步分析[J]. 工业建筑,2002,32 (12) :83–85. KANG Guang-zong, QI Yue-ran, LIU Jun. Analyzing on the Strength Reduction Factor of Axially Loaded RC Column Reinforced by Increasing Section Area[J]. Industrial Construction, 2002, 32 (12) : 83–85 . |
| [15] | 盛光复, 任迎春, 赵艳红. 加大截面加固RC轴心受压构件的强度计算[J]. 四川建筑科学研究,2004,30 (2) :26–28. SHENG Guang-fu, REN Ying-chun, ZHAO Yan-hong. Strength Calculation of Axial Compressive RC Members Strengthened with Increasing Section Method[J]. Sichuan Building Science, 2004, 30 (2) : 26–28 . |
| [16] | TAKEUTI A R, HANAI J B D, MIRMIRAN A. Preloaded RC Columns Strengthened with High-Strength Concrete Jackets Under Uniaxial Compression[J]. Materials & Structures, 2008, 41 (7) : 1251–1262 . |
| [17] | 李黎明. 矩形钢管混凝土柱力学性能研究 [D]. 天津:天津大学,2007. LI Li-ming. Study on Mechanical Performance of Concrete-filled Rectangular Steel Tubes [D]. Tianjin: Tianjin University, 2007. |
| [18] | 刘涛. 碳纤维(CFRP)布加固混凝土矩形柱的性能研究 [D]. 上海:上海大学,2006. LIU Tao. Study on Performance of Rectangular Concrete Columns Reinforced with CFRP [D]. Shanghai: Shanghai University, 2006. |
| [19] | 郭瑞峰. 碳纤维约束钢筋混凝土圆柱及方柱本构模型 [D]. 哈尔滨:哈尔滨工业大学,2010. GUO Rui-feng. Constitutive Models of CFRP-confined Reinforced Concrete Circular and Square Columns [D]. Harbin: Harbin Institute of Technology, 2010. |
| [20] | 孙昊. 套箍技术加固既有钢筋混凝土拱桥的试验研究 [D]. 成都:西南交通大学,2011. SUN Hao. Experimental Research on Hooping Strengthening Technique for Existing Reinforced Concrete Arch Bridge [D]. Chengdu:Southwest Jiaotong University, 2011. |
| [21] | GB 50010-2010,混凝土结构设计规范 [S]. GB 50010-2010, Code for Design of Concrete Structure [S]. |
| [22] | CAMPIONE G, FOSSETTI M, GIACCHINO C, et al. RC Columns Externally Strengthened with RC Jackets[J]. Materials & Structures, 2014, 47 (10) : 1715–1728 . |
| [23] | PAPANIKOLAOU V K, STEFANIDOU S P, KAPPOS A J. The Effect of Preloading on The Strength of Jacketed R/C Columns[J]. Construction & Building Materials, 2013, 38 (1) : 54–63 . |
 2016, Vol. 33
2016, Vol. 33
