扩展功能
文章信息
- 王 勇,李康宁,刘 永,林 鹰
- WANG Yong, LI Kang-ning, LIU Yong, LIN Ying
- 基于断裂点模型的物流节点空间吸引范围划分研究
- Study on Logistics Nodes Spatial Attracting Scope Partition Based on Breakpoint Model
- 公路交通科技, 2016, Vol. 33 (6): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 152-158
- 10.3969/j.issn.1002-0268.2016.06.025
-
文章历史
- 收稿日期:2015-06-18
物流节点是物流系统的重要组成部分,在现代物流网络中起着越来越重要的作用。在物流节点上不仅要完成装卸搬运,保管等环节的运作,也要处理服务范围内的车辆调度和信息反馈等。因此,确定空间吸引范围有利于物流节点整合车辆调度信息,优化车辆路径,合理安排各环节的有效衔接进而提高物流系统的整体运作效率。
目前国内外学者对物流行业空间吸引范围的研究多集中于区域、城市层面,如刘荷和王健[1]、侯赟慧等[2]利用引力模型研究了区域和城市间的经济联系强度;杨家其[3]运用引力模型研究了港口腹地划分问题;韩瑞玲等[4]基于引力模型结合区域经济发展水平对东北物流市场分割进行了研究;JI和HE[5] 对以港口为节点的区域物流与其所在地区的区域经济相互影响、协调发展情况进行了研究;John[6]对两家知名快递企业的网络结构进行空间分析和前景预测。通过上述研究可以发现,对空间吸引力范围的研究较少涉及物流节点,并且在确定空间吸引范围过程中,多应用传统的空间划分模型[7],带有一定的主观性且精确度不高。
本文采用断裂点模型结合泰森多边形理论研究了多物流节点空间吸引力范围划分问题。首先运用含有主观约束条件的拉开档次法对物流节点质量重新构建,考虑物流节点的区位条件和规模条件,使物流节点质量更具实际意义。其次,运用断裂点到两端点距离对泰森多边形进行加权,确定了物流节点空间划分的方法,提高了划分的精确性。最后由物流节点质量确定的划分顺序并对物流节点空间吸引范围进行划分。
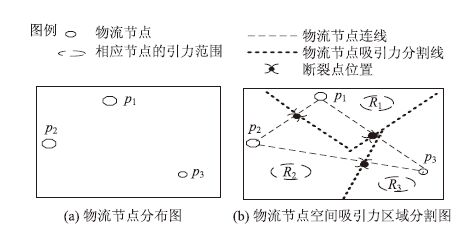
1 研究问题阐述已有物流行业区域划分研究较少涉及物流节点(物流园区、物流中心等)这一微观层面。但从我国整体来看,在城市或区域内还存在着局部物流发展失衡、物流节点分布不均和服务水平差异大等现象,进而导致了区域内物流发展规划不衔接、资源整合障碍等问题[8]。在物流网络中,一般根据物流节点的定位功能不同分为主次物流节点[4, 5, 6, 7, 8, 9]要进行分层次研究,而本文研究的是同一层次的物流节点,不涉及主次关系。其次文中选取的物流节点分属于同一经济区域内的不同地区,由于经济发展、生产消费流通和交通条件等指标因素的不同,对不同地区物流节点发展的影响程度也有所不同。因此将地区指标因素对物流节点的影响加入到物流节点空间范围划分研究中非常有必要。以物流节点为研究对象,结合断裂点模型与泰森多边形理论对空间范围进行划分,如图 1所示。在图 1(a)中,P1,P2,P3表示区域内3个物流节点位置分布,图 1(b) 中R1,R2,R3 区域是应用断裂点模型与泰森多边形理论划分得到的P1,P2,P3的空间吸引范围。
|
| 图 1 物流节点空间吸引范围划分图 Fig. 1 Partition diagram of logistics nodes spatial attracting scope |
地区经济发展水平决定了地区物流量的大小,影响区域物流发展水平,而物流节点规模水平又直接影响其发展水平和服务范围,因此,研究不同物流节点的空间引力范围就需要考虑地区物流发展水平的影响因素和物流节点的规模水平。文中物流节点的“质量”由两部分构成:一是代表物流节点所处地区物流发展水平的“区位质量”;二是代表物流节点规模水平的“规模质量”。
2.1.1 “区位质量”指标体系构建根据指标的可获取、可比较、定性定量相结合原则,借鉴相关文献[10, 11, 12],从经济发展、生产消费流通、交通条件3个方面构建“区位质量”的指标体系,如表 1所示。
| 指标 | 指标量 | 子指标 |
| 经济发展 a | a1 | GDP |
| a2 | GNP | |
| a3 | 固定资产投资总额 | |
| a4 | 工业固定资产投资总额 | |
| a5 | 工业能源消费总量 | |
| 生产消费流通b | b1 | 总人口数 |
| b2 | 社会消费品总额 | |
| b3 | 农业生产总值 | |
| b4 | 工业生产总值 | |
| b5 | 第三产业生产总值 | |
| 交通条件c | c1 | 境内公路里程数 |
| c2 | 路网密度 | |
| 注:文中指标因素主要来源《重庆统计年鉴2014》 | ||
为了确定区位质量,应用主成分分析法对表 1中的指标数据进行分析。主成分分析法一般选取贡献率累计达到85%以上的前z个主成分指标进行计算。其中为取得“区位质量”,对各地区在主成分上的得分进行加权求和,权重由式(1)确定:
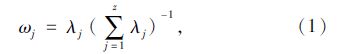
第w个地区的“区位质量”为:

式中,j为主成分数量,取值为(1,2,…,z); w为地区数量,取值为(1,2,…,k); λj表示第j个主成分的特征根; pwj是指第w个区域在主成分j上的得分。
2.1.2 “规模质量”指标的选取本文选取物流节点的面积、入驻商家数量、从业人员数量、库存容量和库存租金来构建物流节点规模质量的指标体系。
首先用公式(3)消除观测值uij量纲影响
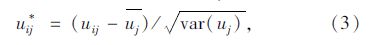
式中,$\operatorname{var}\left( {{u}_{j}} \right)={{\sum\limits_{i=1}^{n}{\left( {{u}_{ij}}-{{{\bar{u}}}_{j}} \right)}}^{2}}/\left( m-1 \right)$, i为物流节 点,取值为(1,2,…,n); j为指标,取值为(1,2,…,m)。 则标准观测值矩阵 B =(uij*)n×m, 各指标权重采用德尔菲法[13]进行确定。则第i个物流节点的“规模质量”为:

拉开档次法在几何中解释为:n个评价指标构成的n维评价空间,m个被评价对象是n维评价空间中的点。根据n维评价空间构造一个最佳的一维空间,使得各点在一维空间上的投影点最为分散的向量为最优解。
y=ω1x1+ω2x2+…+ωnxn= W T X 表示极大型评价指标X1,X2,…,Xn的综合评价函数。W=(ω1,ω2,…,ωn)T表示n维权系数向量,X=(x1,x2,…,xn)T 表示被评价系统的状态向量,xij(i=1,2,…m; j=1,2,…,n)表示第i个评价对象的xj评价指标的观测值。为了消除不同类型指标之间的不可公度性,将观测值进行无量纲化处理。郭亚军等[14]研究表明不同的无量纲处理方法会使得拉开档次法的评价结果和效果产生变化。根据拉开档次法被评价对象整体差异越大评价效果越好的特点,采用线性比例法进行无量纲化处理转化为标准观测值,公式如下:

式中αj为第j评价指标观测值中的最小值。
如果第i个系统的n个标准观测值x′i1,x′i2,…,x′in代入综合评价函数式,即得:
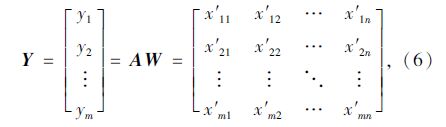
式中,Y为指标评价矩阵,A为指标观测矩阵。
确定权系数向量 W=(ω1,ω2,…,ωn)T的准则是体现出各个评价对象的最大差异,即使指标的状态向量 X=(x1,x2,…,xn)T的线性函数yi的取值的方差或分散 程度尽可能大。因此,m个被评价对象取值构成样本的方差为:
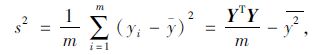
由此得到:
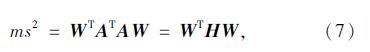
式中,H 为A的转置与A乘积得到的实对称矩阵。
显然,当对ω不加限定时式(10)可取任意大的值,因此限定WTW=1,W>0可求得权重值。由以上的步骤可看出拉开档次法是基于“差异驱动”的赋权方法,应用了客观的数学理论与方法,却没有考虑评价或决策中发挥重要作用的评价者主观信息。而评价者由于经验、知识、偏好等因素不能给出确定的权重值,但却可以给出权重之间某些模糊或者定性的关系[15](如ωi>ωj,i≠j)将这种关系用函数表示为:
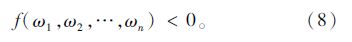
将式(7)、(8)以及限定条件结合起来,得到主观信息嵌入的权重方程:
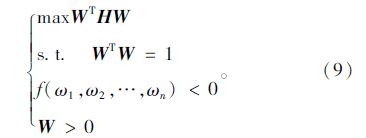
由于考虑规模质量和区位质量两个指标,本文中n的值设定为2,求得权系数向量,因此第i物流节点质量为:
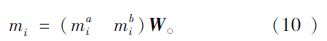
断裂点模型是在引力模型的基础上演化而来,引力模型中引力的大小由两研究对象的质量和距离决定,与质量成正比与距离成反比,而两研究对象引力达到的平衡点即为断裂点。其模型如下:
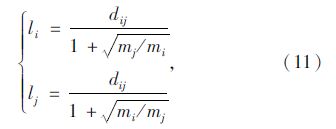
式中,li,lj分别代表断裂点到i和j的距离; dij为i和j之间的距离; mi,mj分别代表i和j的质量。
泰森多边形法[16, 17]是对空间平面的一种划分方法,它形成的任意凸多边形中含有一个发生点Pi,任意内点到该凸多边形发生点Pi的距离都小于该点到其他任何发生点Pj的距离,而这些发生点就叫泰森多边形的发生元。而到相邻两发生元距离相等的点构成的图形为泰森多边形,即相邻两发生元连线的垂直平分线围成的图形。
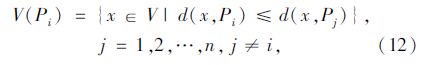
式中,Pi为二维空间V上的点集合,i=1,2,…,n;x是空间上的点;d(x,Pi)为点x到Pi的距离函数。
借鉴泰森多边形理论以相邻两点取垂直平分线的区域划分集成方法,以一定的顺序由pipj连线dij上断裂点处做垂线的方法来划分整个区域,使得每个多边形内含有一个点。不同的划分顺序会导致区域划分结果不同,因此,划分顺序需要提前确定。由于节点质量对吸引范围的划分起到决定性作用,因此本研究以物流节点的综合质量大小确定划分顺序。按照综合质量大小将各点进行排列得到pi*,则按照以下规则进行划分:
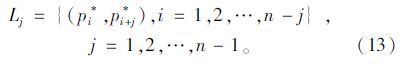
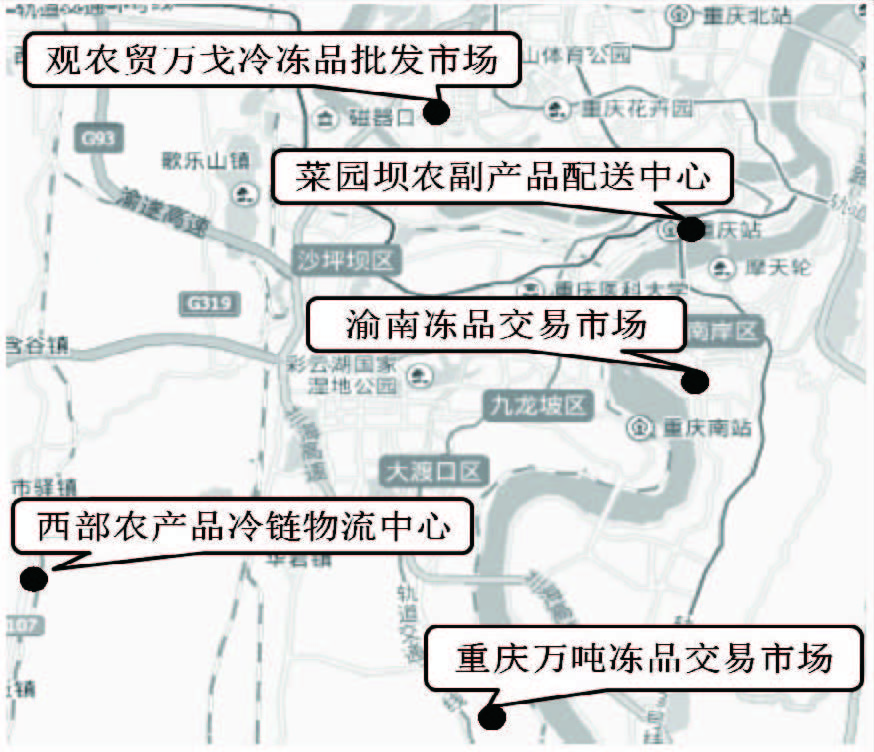
选取重庆主城区及其周边区域范围内的5个冷链物流节点进行空间吸引范围划分研究。5个冷链物流节点分别为九龙坡、大渡口区、南岸区、渝中区和江北区的西部农产品冷链物流中心。 重庆万吨冻品交易市场、渝南冻品交易市场、 菜园坝农副产品配送中心和观农贸万戈冷冻品批发市场,分别用P1,P2,P3,P4,P5表示。其在重庆市的分布如图 2所示。
|
| 图 2 重庆市主要冷链物流节点分布图 Fig. 2 Distribution of main cold chain logistics nodes in Chongqing |
以2014年重庆主城区及其周边11个区县城市的数据资料作为基础,应用主成分分析方法,对11个区县的综合得分进行判定。输出表 2为特征根统计表,表示主成分的贡献率;表 3为主成分载荷表,表示主成分变量对相应原变量的相对重要程度。由表 2可以看出:3个主成分的贡献率分别为48.894%,30.405%,10.862%,累计方差贡献率为90.161>85%,即可用这3个主成分代替原来12个经济指标。由表 3可以看出,第一主成分载荷最大的是公路里程数;第二主成分主要有 GDP。
| 主成分 | 特征根 | 贡献率/% | 累计贡献率/% |
| 1 | 5.867 | 48.894 | 49.894 |
| 2 | 3.649 | 30.405 | 79.299 |
| 3 | 1.303 | 10.862 | 90.161 |
| 主成分因子 | |||
| 1 | 2 | 3 | |
| a1 | -0.202 | 0.968 | -0.050 |
| a2 | -0.745 | 0.547 | 0.272 |
| a3 | 0.529 | 0.642 | -0.478 |
| a4 | 0.871 | 0.120 | -0.187 |
| a5 | 0.748 | 0.608 | 0.208 |
| b1 | 0.705 | 0.104 | 0.534 |
| b2 | -0.551 | 0.800 | 0.146 |
| b3 | 0.896 | 0.172 | 0.345 |
| b4 | 0.348 | 0.658 | -0.564 |
| b5 | -0.660 | 0.618 | 0.355 |
| c1 | 0.914 | 0.283 | 0.176 |
| c2 | -0.823 | 0.197 | -0.141 |
计算各区县在3个主成分上得分,并按各主成分的贡献率,将特征根λ的值代入式(1),计算3个主成分的权重为(0.518,0.355,0.127),然后用式(2)结合表 2与各地区在主成分上得分计算综合评价值。为保证物流质量为正值,将总得分线性平移2个单位,得到区位质量得分值[1],如表 4所示。
| 地区 | 1得分 | 2得分 | 3得分 | 质量 |
| 渝中区 | -1.798 | 0.757 | 1.691 | 1.484 |
| 大渡口区 | -0.526 | -2.059 | 0.204 | 1.045 |
| 江北区 | -0.703 | -0.048 | -0.121 | 1.588 |
| 沙坪坝区 | -0.529 | 0.418 | -0.834 | 1.753 |
| 九龙坡区 | -0.263 | 0.775 | 0.253 | 2.149 |
| 南岸区 | -0.462 | -0.042 | -0.585 | 1.665 |
| 北碚区 | 0.348 | -0.740 | -0.512 | 1.878 |
| 渝北区 | 0.602 | 1.734 | -1.287 | 2.757 |
| 巴南区 | 0.727 | -0.160 | 0.120 | 2.355 |
| 江津区 | 2.019 | 0.243 | 1.854 | 3.400 |
| 璧山县 | 0.586 | -0.877 | -0.783 | 1.927 |
结合冷链物流节点特点,选取面积(万平方米)、入驻商家数量(个)、从业人员数量(个)、冷库容量(万吨)和冷库月租金(元/平方米)来构建物流节点规模质量的指标体系,指标数据值如表 5所示。
| 节点名称 | 面积/(×104 m2) | 入驻商家/个 | 从业人员/个 | 冷库容量/(×104 t) | 月租金/(元·m-2) |
| P1 | 43 | 460 | 8 000 | 23 | 60 |
| P2 | 26 | 500 | 5 000 | 10 | 140 |
| P3 | 3.8 | 300 | 1 800 | 3 | 120 |
| P4 | 5 | 300 | 1 500 | 1 | 80 |
| P5 | 3 | 210 | 1 600 | 1.5 | 110 |
由于各指标的量纲不同,需要对原始数据结合式(4)进行标准化处理来消除量纲影响[18],然后根据德尔菲法,确定各指标权重为(0.2,0.12,0.18,0.21,0.29),最后根据式(5)求得物流节点规模质量,如表 6所示。
| 节点 名称 | 面积/ (×104 m2) | 入驻 商家 | 从业 人员 | 冷库容量/(×104 t) | 月租金/ (元·m-2) | 质量 |
| P1 | 1.508 | 0.872 | 1.532 | 1.648 | -1.37 | 1.630 |
| P2 | 0.553 | 1.201 | 0.506 | 0.248 | 1.029 | 1.696 |
| P3 | -0.694 | -0.44 | -0.59 | -0.51 | 0.343 | 0.695 |
| P4 | -0.627 | -0.44 | -0.69 | -0.72 | -0.69 | 0.347 |
| P5 | -0.739 | -1.18 | -0.76 | -0.67 | 0.686 | 0.632 |
| 权重 | 0.2 | 0.12 | 0.18 | 0.21 | 0.29 |
通过数据调研和分析,得知规模水平对物流节点空间吸引力范围的影响比区位条件大,因此式(8)可改写为ωa<ωb并将其代入式(9),然后根据式(5)、(9)以及表 4、表 6的数据求得mia和mib的权重系数向量 W = (0.298,0.702)T,最后通过式(10)的数据求得各物流节点的质量如表 7所示。
| 质量 | P1 | P2 | P3 | P4 | P5 |
| mia | 2.057 | 1 | 1.594 | 1.420 | 1.520 |
| mib | 4.704 | 4.895 | 2.006 | 1 | 1.824 |
| mi | 3.915 | 3.734 | 1.883 | 1.125 | 1.734 |
首先确定冷链物流节点之间的直线距离dij,根据图 1所示冷链物流节点的具体分布,测得各节点之间的距离。然后将表 7中物流节点的质量mi和dij距离带入式(11),可得出5个冷链物流节点的断裂点位置。最后按照物流节点的质量大小进行排序为:p1,p2,p3,p5,p4,并根据式(13)确定划分顺序,如表 8所示。
| 物流节点 | 顺序 | 两点距离/km | 断裂点位置/km |
| (P1,P2) | 1 | 13.8 | 6.98 |
| (P1,P3) | 5 | 20.7 | 12.22 |
| (P1,P4) | 10 | 20.6 | 13.41 |
| (P1,P5) | 8 | 19.3 | 11.591 |
| (P2,P3) | 2 | 11.8 | 6.899 |
| (P2,P4) | 9 | 14.5 | 9.361 |
| (P2,P5) | 6 | 18.6 | 11.063 |
| (P3,P4) | 7 | 4.3 | 2.425 |
| (P3,P5) | 3 | 11.2 | 5.716 |
| (P4,P5) | 4 | 7.1 | 3.168 |
| 注:表中断裂点位置是指断裂点到(pi,pj)中点pi的距离。 | |||
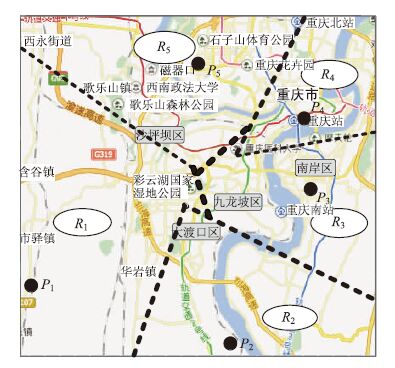
应用表 8中数据对物流节点的空间吸引范围进行划分,如图 3所示。图中R1,R2,R3,R4,R5分别表示物流节点p1,p2,p3,p4,p5的空间吸引范围。
|
| 图 3 重庆市主要冷链物流节点空间吸引范围划分图 Fig. 3 Spatial attracting scope partition figure of main cold chain logistics nodes in Chongqing |
图 3即为重庆市主城区五大冷链物流节点的区域划分范围,通过实地调研,该划分范围与上述五大物流节点的实际服务范围具有较高的吻合度。该方法也可用于类似物流节点的区域范围划分中。
4 结论运用断裂点模型结合泰森多边形理论确定合理的空间划分方法,并基于节点质量大小确定空间划分顺序,使结果更加精确,与实际有较高的吻合度。这为解决类似物流节点的空间吸引范围划分问题提供了借鉴。同时,可以在空间吸引范围划分和区域利益最大化的基础上,对区域内物流节点进行整体规划,整合区域供应链、均衡区域物流发展,提高区域竞争力。
通过研究可知物流节点自身规模水平对其空间吸引力的影响比区位条件更大。因此加强冷链物流节点自身基础设施建设,提高服务水平,更有利于增大空间吸引范围,在区域竞争中占取更大的市场份额、获取有利市场地位。
| [1] | 刘荷,王健.基于轴辐理论的区域物流网络构建及实证研究[J].经济地理,2014,34(2):108-113. LIU He,WANG Jian. The Construction of Regional Logistics Networks and Its Empirical Research Based on Hub-and-Spoke Theory[J].Economic Geography,2014,34(2):108-113. |
| [2] | 侯赟慧,刘志彪,岳中刚.长三角区域经济一体化进程的社会网络分析[J].中国软科学,2009(12):90-101. HOU Yun-hui,LIU Zhi-biao,YUE Zhong-gang. Social Network Analysis over the Process of Economic Integration in the Yangtze River Delta[J]. China Soft Science,2009(12):90-101. |
| [3] | 杨家其.基于模糊综合评判的现代港口腹地划分引力模型[J].交通运输工程学报,2002,2(2):123-126. YANG Jia-qi. Gravity Model for Partitioning Port Hinterlands Based on Fuzzy Comprehensive Evaluation[J].Journal of Transportation Engineering,2002,2(2):123-126. |
| [4] | 韩瑞玲,于建辉.基于引力模型的东北地区物流市场分割及应用[J].干旱区资源与环境,2012,26(10):169-173. HAN Rui-ling,YU Jian-hui.Logistics Market Segmentation Based on Gravity Model and Its Application to Northeast China[J]. Journal of Arid Land Resources and Environment,2012,26(10):169-173. |
| [5] | 计明军,贺茂英. 基于双层规划的动态腹地二级港口物流网络优化[J]. 交通运输系统工程与信息,2010,10(6):89-94. JI Ming-jun,HE Mao-ying. Optimization of Two-Stage Port Logistics Network of Dynamic Hinterland Based on Bi-level Programming Model[J]. Journal of Transportation Systems Engineering and Information Technology,2010,10(6):89-94. |
| [6] | BOWEN J T, Jr. A Spatial Analysis of FedEx and UPS:Hubs,Spokes,and Network Structure[J]. Journal of Transport Geography,2012,24(3):419-431. |
| [7] | 丁涛,代舒,蒋军.基于引力模型和群决策理论的物流园区空间吸引范围[J].水运工程,2009(12):24-27. DING Tao,DAI Shu,JIANG Jun. Discussion of Spacial Attracting Scope of Logistics Park Based on Gravity Model and Theory of Group Decision[J].Port and Waterway Engineering,2009(12):24-27. |
| [8] | 张芳霞,朱志玲,张晓霞.银川市产业集聚与城市空间结构优化研究[J].干旱区资源与环境,2011,25(2):34-39. ZHANG Fang-xia,ZHU Zhi-ling,ZHANG Xiao-xia. Optimization of Industrial Cluster and Urban Spatial Structure of Yinchuan City[J]. Journal of Arid Land Resources and Environment,2011,25(2):34-39. |
| [9] | 胡青蜜,胡志华,陶莎.二级轴辐式零担物流网络设计的资源均衡利用问题[J].公路交通科技,2013,30(4):124-131. HU Qing-mi,HU Zhi-hua,TAO Sha. Resource Balanced Usage Problem for Bi-level Hub-and-spoke LTL Logistics Network Design[J]. Journal of Highway and Transportation Research and Development,2013,30(4):124-131. |
| [10] | 谢如鹤,邱祝强,陈宝星.区域物流产业竞争力指标体系及其应用[J].工业工程,2008,11(1):109-112. XIE Ru-he,QIU Zhu-qiang,CHEN Bao-xing. Index System and Its Application for the Competitiveness of Regional Logistics Industry[J]. Industrial Engineering Journal,2008,11(1):109-112. |
| [11] | 李全喜,金凤花,孙磐石.区域物流引力和地位模型的构建及应用研究[J].经济地理,2010,30(10):1619-1624,1630. LI Quan-xi,JIN Feng-hua,SUN Pan-shi. Construction and Application of Regional Logistics Gravity Model and Regional Logistics Status Model[J]. Economic Geography,2010,30(10):1619-1624,1630. |
| [12] | 丁伟,张亮,李健.轴-辐式现代物流网络构建及实证分析[J].中国软科学,2010(8):161-168. DING Wei,ZHANG Liang,LI Jian. The Construction of Hub-and-Spoke Logistics Networks and Its Empirical Research[J]. China Soft Science,2010(8):161-168. |
| [13] | 成耀荣,单华夷,刘丰根.物流园区辐射范围的确定及物流量分摊计算[J]. 交通运输工程学报,2008,8(6):122-126. CHENG Yao-rong,SHAN Hua-yi,LIU Feng-gen. Acting Sphere Determination of Logistics Park and Allocation Calculation of Logistics Volume[J]. Journal of Traffic and Transportation Engineering,2008,8(6):122-126. |
| [14] | 郭亚军,马凤妹,董庆兴.无量纲化方法对拉开档次法的影响分析[J].管理科学学报,2011,14(5):19-28. GUO Ya-jun,MA Feng-mei,DONG Qing-xing. Analysis of Influence of Dimensionless Methods on Deviation Maximization Method[J]. Journal of Management Sciences in China,2011,14(5):19-28. |
| [15] | 戚宇,郭亚军,郭英民.主观信息嵌入式的拉开档次法及其应用[J].东北大学学报:自然科学版,2011,32(7):1057-1060,1064. QI Yu,GUO Ya-jun,GUO Ying-min. The Scatter-Degree Method of Subjective Information Insertion Type and Its Application[J]. Journal of Northeastern University:Natural Science Edition,2011,32(7):1056-1060,1064. |
| [16] | 张仪彬,吴刚,赵佳虹, 等. 基于加权Voronoi图的物流园区腹地界定[J]. 公路交通科技,2012,29(10):154-158. ZHANG Yi-bin,WU Gang,ZHAO Jia-hong,et al. Definition of Logistics Park Hinterland Based on Weighted Voronoi Diagram[J].Journal of Highway and Transportation Research and Development,2012,29(10):154-158. |
| [17] | LONG Xiao-qiang,ZHANG Yi-bin,CHEN Yan-ru. Using Voronoi Diagram in Construction the Scope of Logistics Park Hinterland:an Engineering Application[J]. Systems Engineering Procedia,2011, 10(2):69-76. |
| [18] | 刘静,毛海军.可拓学理论在区域物流发展评价中的应用[J].公路交通科技,2010,27(10):148-152. LIU Jing,MAO Hai-jun. Application of Extenics in Evaluation of Regional Logistics Development[J]. Journal of Highway and Transportation Research and Development,2010,27(10):148-152. |
 2016, Vol. 33
2016, Vol. 33
