扩展功能
文章信息
- 谷金晶,杨 艳,张敬东
- GU Jin-jing, YANG Yan, ZHANG Jing-dong
- 考虑到站时间差的多层级常规公交时刻表
- Timetable of Multi-level Transit Considering Arrival Time Difference
- 公路交通科技, 2016, Vol. 33 (6): 128-133
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 128-133
- 10.3969/j.issn.1002-0268.2016.06.021
-
文章历史
- 收稿日期:2015-07-06
居民多样化出行,要求公交运能应适应居民的不同需求,公交服务应更加精细化。在分析道路交通状况与居民出行特征的基础上,提出相对适应的多层级常规公交线网系统由大站快车、干线公交、支线公交、社区公交和专线公交5个层级组成,既有疏通性功能,又有服务性功能[1]。该公交体系统具有线路分层级、多元化的特点,对运营调度方式精确性和柔性的要求也相应增加。公交运行时刻表是连接公交企业与乘客之间的纽带,通过提供有效的换乘衔接,整合不同层级的公交线路,协调层级间公交线网的换乘衔接,既可保证特定时间段内的运输效率,又可实现运输资源的优化配置。
国内外学者对多线路公交协调时刻表编制问题的研究,多集中考虑使所有公交线路上的运营车辆最大同步到达。Adamski[2]对在换乘点的同步换乘和在共同路段行驶的不同线路的协同这两种调度问题建模,采用遗传算法求解了模型。Ceder[3]在确定的发车频率和有限的公交车运力条件下,建立了不同线路公交车辆在换乘站点的相遇次数最大模型,编制出发车时刻表。Fleurent[4]从最小、最大和理想3种换乘时间角度考虑了同步换乘质量指标,采用拉格朗日松弛算法和启发式算法求解了模型。覃运梅[5]和石琴[6]从总相遇点数最小和最大同步性换乘角度,分别构建了混合整数非线性规划和多目标优化模型。杨丽[7]将区域发车时刻表编制归结为有容量限制的多重0-1背包问题,以换乘价值为导向,编制出区域调度范围内换乘服务品质最优的时刻表。司徒炳强[8]考虑公交线路之间合作与竞争关系下的公交网络行车时刻表优化模型,并考虑乘客等车时间的多线路组合行车时刻表编制了模型,分别采用蚁群算法进行了模型求解。陈霞[9]分析了公交线网结构与公交车辆的同步到达关系,构建了换乘点换乘车辆数最大模型,采用遗传算法求解了模型。何迪[10]以最大程度协调了区域内各公交线路上的车辆,并以公交乘客在主要换乘站点的等待时间之和最少为优化目标,构建了整数规划模型。Ibarra[11]和柏海舰[12]从同时到站次数和车辆数最大角度构建了时刻表编制模型。
本文在多层级常规公交线网布局规划背景下,以各个层级的公交线网为区域调度单元,明确区域调度的范围和对象,对在换乘站点处有衔接关系的公交服务特性和线路之间的关系进行分层说明,细分时间差,有的放矢地优化层级间公交线路的到站 时间。根据线路间的层级服务关系来协调确定到达 换乘站点的时间,而不单纯追求同时到达同一换乘站点的车辆或次数最大。同时统筹考虑发车时刻与发车间隔,使编制出的时刻表能更好地满足多层级常规公交的实际运营需要。
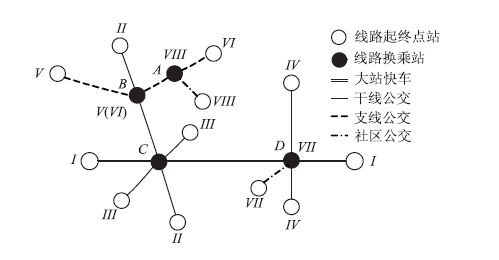
1 多层级常规公交线网布局及运营特性 1.1 多层级常规公交线网布局多层级常规公交网络布局模式如图 1所示。
|
| 图 1 多层级常规公交网络布局图 Fig. 1 Layout of multi-level transit network |
图 1中以大站快车、干线公交为疏通性公交主体。支线公交、社区公交除自身服务功能外,还对上一级公交系统输送和承接乘客,在公交运输服务体系中起着重要的微循环作用[13]。多层级常规公交线网在物理上整合为一个系统,可减少乘客的换乘次数,同时可提供多样化的公交服务。B和C为同层级公交线路换乘站点,A和D为层级间公交线路换乘站点。层级间线路的集散关系尤为关键,各层级公交线路在换乘站点处的衔接效能对整体线网运营服务影响很大。
1.2 多层级常规公交运营特性多层级常规公交线网换乘模式由以路段换乘为主的服务模式,逐渐向分级集散的模式转变。依据换乘模式的不同,将多层级公交线路的运营特性归纳为表 1。
| 分类依据 | 有换乘 | 无换乘 | |||
| 线路层级 | 大站快车 | 干线公交 | 支线公交 | 社区公交 | 专线车 |
| 运行道路 | 快速路、主干道 | 主干道 | 次干道 | 社区道路 | 各种道路 |
| 线路形状 | 弯曲少、迂回少 | 允许适当弯曲和迂回 | 允许弯曲和迂回 | 允许弯曲和迂回 | 允许弯曲和迂回 |
| 运送速度/(km·h-1) | >25 | 20~25 | 15~20 | <15 | 依乘客需求定 |
| 线路长度/km | >15 | 8~15 | <8 | 0.3~0.5 | 依乘客需求定 |
| 站间距/km | >1.0 | 0.5~1.0 | 0.3~0.5 | <0.3 | 依乘客需求定 |
| 调度优化目标 | 直达客流量最大 | 换乘效率最高 | 换乘效率最高 | 换乘效率最高 | 换乘次数最少 |
多层级常规公交运行时刻表编制的核心问题是在一个特定时间段内,实现乘客换乘时间最小化的多条公交线路协同发车。公交线路按照服务特性归属不同层级,将整个线网分层分块地划分为若干层级作为优化调度单元。编制行车时刻表时,既要考虑同一层级内单一线路上的乘客出行需求,又要兼顾乘客在不同层级公交线路间的换乘需求,同时还要尽量保证每条线路的客流均衡,以更好地实现乘客和企业双赢。专线公交将一部分乘客从公交线路中剥离出去,在增加整个体系公交服务灵活性的同时,保证剩余4个层级公交运营在一定范围内乘客出行的稳定性。
对同一层级内的公交线路,基于对换乘站点容量和上一层级公交服务均衡性的考虑,并避免多辆无换乘关系的车辆同时到达而造成站台处乘车混乱,编制时刻表时应侧重错时到达。下一层级公交线路向上一层级公交集散乘客,即层级间公交线路存在换乘关系,需着重考虑乘客等车时间的多线路组合协同发车,使不同层级公交车辆同时到达同一换乘站点。相对于单线调度,区域调度中公交时刻表的编制在确定了各条线路的发车间隔后,还要尽量考虑减少乘客在不同线路交叉点处的换乘等待时间。
因此,本文以公交线路层级间的服务关系不同作为划分多线路协同发车的准则,基于到达同一换乘站点的时间差,分别研究层级内与层级间多条线路公交始发车时刻和发车间隔模型,编制出适用于多层级常规公交的运行时刻表。
2.2 模型假设(1)优化周期内,车辆的站间行程时间稳定;(2)层级内同一条线路的公交车辆有规律地行驶,无越站和超车等行为;(3)不同层级线路的车辆同时到站,不考虑车辆的停站时间;(4)换乘站点处的乘客只等1条线路的公交车;(5)优化周期内,公交乘客不随公交服务质量的变化而变化;(6)公交乘客利益(成本)与公交企业效益(成本)的重要性是等同的。
3 构建模型本文分别从公交线路的始发车时刻和发车间隔两个方面,构建多层级常规公交运行时刻表优化模型。
3.1 多层级常规公交发车时刻模型 3.1.1 层级内公交始发车时刻模型同一层级内公交线路主要满足同一出行需求服务,同一层级不同线路在同一换乘站点相遇,需要满足换乘公交站台的容量,并能保证公交服务的均衡性。层级内公交线路的发车时刻优化目标应使同一层级内各线路异步到站。以图 1中换乘站点B和C为研究对象,令线路i和线路j的车辆到站时间差为Z1,则有:
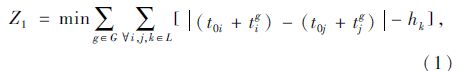
式中,G为公交线网中换乘站点集合;g为公交线网中第g个换乘站点,g∈G;L为公交线路集合,L={L1,L2,…,Ln}; n为公交线路编号,n={I,II,…,VIII};i,j,k分别为公交线网中第i条、第j条和第k条线路,i,j,k∈L,且i≠j≠k;线路i与线路j属于同一层级公交线路;k属于比i和j高层级的公交线路;t0i,t0j分别为优化周期内线路i和线路j的始发车时刻;tig,tjg分别为线路i和线路j车辆从始发站到站点g的行程时间;hk为线路k的发车间隔。
从线路的始发车时刻、发车间隔、站点容纳能力3个方面,得到如下约束条件:
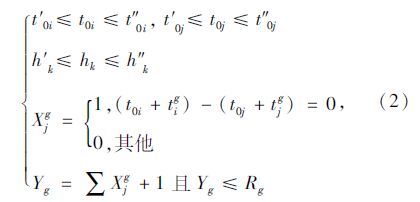
式中,t′ 0i,t′ 0j为线路i和线路j的最早始发车时刻;t″ 0i,t″ 0j为线路i和线路j的最迟始发车时刻;h′ k为线路k的最小发车时间间隔;h″ k为线路k的最大发车时间间隔;Xjg为与线路i同时到站点g的线路j的车辆数;Yg为同时到达站点g的所有线路数量;Rg为站点g的容纳能力。
3.1.2 层级间公交始发车时刻模型乘客需要换乘的两个层级公交,如果不同时到达换乘站点,将会产生乘客在站点的候车时间,损失乘客利益,并浪费公交资源。层级间的集散关系是双向的,可通过调整各线路车辆的始发车时刻,使不同层级公交线路车辆到达换乘站点的时间差达到最小。 以图 1中的换乘站点A和D为例,令Z2为非异步到站时间差,构建线路j和线路k的非异步到站时间差最小发车时刻优化模型的目标函数为:
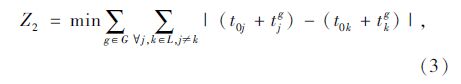
要实现Z2取得最小值,从线路的始发车时刻和站点的容纳能力进行约束,即需要满足:
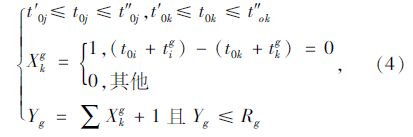
式中,t′0k为线路k的最早始发车时刻;t″0k为线路k的最迟始发车时刻;Xkg为与线路i同时到站点g的线路k车辆数。
3.2 多层级常规公交发车间隔模型 3.2.1 层级内公交发车间隔模型获得线路在优化周期内的始发车时刻后,层级公交客流的不均衡性可以采用发车间隔来协调。通常在一个足够长的时间段内,同一线路车辆使用不同的发车间隔比使用较小的等发车间隔所需的运营总车辆数多,且车辆利用率更低。因此,采用等间隔发车。公交线路最优发车间隔h*的确定主要需要考虑两方面因素:一是公交企业运营费用,本文主要考虑线路上运营的公交车辆数;二是公交乘客换乘候车成本[14],则有:
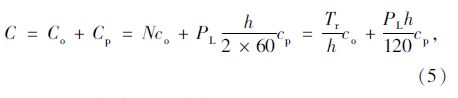
式中,C为线路运营总成本;Co为公交企业运营费用;Cp为公交乘客等车成本;N为运营公交车辆数;co和cp分别为单位小时企业运营成本和乘客成本;PL为线路车辆上单位小时乘客数量;h为车辆发车间隔;Tr为优化周期。
对发车间隔h求导,并令导数为零,得到公交线路最优发车间隔h*:
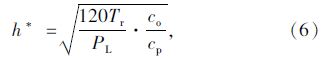
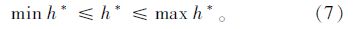
当多条公交线路汇合到1条线路上时,该条公交线路发车频率为多条公交线路发车频率的总和,即有:
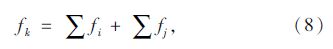
式中,fi,fj,fk分别为线路i,j,k的发车频率。
线路k所属层级公交线路区段的平均联合发车间隔计算公式为:
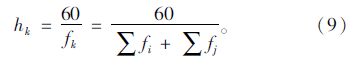
(1)公交行车计划及运营参数集
公交行车计划及运营参数集合={换乘站点集合;公交线路集合;公交线路层级;线路始发车时刻;线路最早始发车时刻;线路最迟始发车时刻;各线路车辆从始发站到站点的行程时间;站点容纳能力;线路发车间隔;线路最小发车时间间隔;线路最大发车时间间隔;单位小时企业运营成本;单位小时企业乘客成本;线路车辆上单位小时乘客数量}。
(2)生成初始种群
计算各条公交线路的最小发车间隔h′和最大发车间隔h″,列举出各条线路所有可能的发车间隔h。
(3)适应度函数
适应度函数是区分个体优劣的标准,通过对目标函数进行变换,得到个体的适应度值为目标函数值的倒数,即
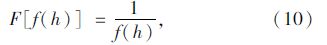
式中,F[f(h)]为个体适应度函数值;f(h)为函数值。
(4)遗传算法
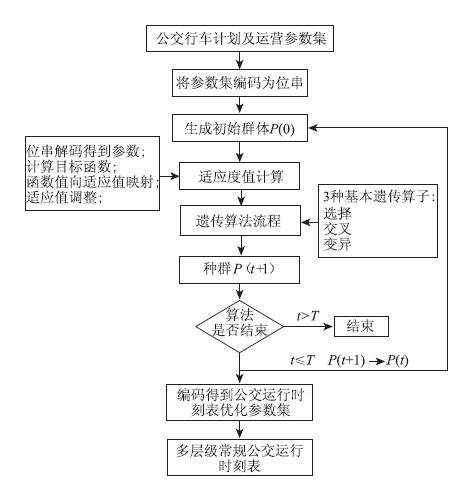
遗传算法的计算流程如图 2所示。
|
| t—种群代数;P(t)—当前种群;P(t+1)—下一代种群;T—遗传算法执行的最大迭代次数。 图 2 遗传算法运算流程图 Fig. 2 Flowchart of genetic algorithm operation |
图 1中的多层级常规公交线网包含8条线路(分别以I,II,…,VIII表示)和4个换乘站点(分别以A,B,C,D表示)。m1,m2,m3,m4依次表示大站快车、干线公交、支线公交和社区公交线路的层级。案例中,m1= {I};m2= {II,III,IV};m3={V,VI};m4= {VII,VIII}。站点的容纳能力分别为2,2,2,3辆公交车,令Tr为1 h,4个换乘站点的权重相等,根据实际跟车调查和公交公司提供的数据,得到各条公交线路运营参数,如表 2所示。
| 参数 | 线路 | |||||||
| I | II | III | IV | V | VI | VII | VIII | |
| co/[元·(辆·h)-1] | 90 | 80 | 80 | 60 | 50 | 50 | 50 | 40 |
| cp/[元·(人·(h)-1] | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| PL/[人·(辆·(h)-1] | 1920 | 427 | 427 | 320 | 67 | 67 | 67 | 14 |
| 始发车时刻 | 7:00 | 7:20 | 7:20 | 7:45 | 7:00 | 7:00 | 7:30 | 7:00 |
| 发车间隔/min | 5 | 5 | 8 | 8 | 5 | 5 | 8 | 15 |
| tA0/min | — | — | — | — | — | 15 | — | 20 |
| tB0/min | — | 15 | — | — | 25 | 20 | — | — |
| tC0/min | 25 | 20 | 17 | — | — | — | — | — |
| tD0/min | 20 | — | — | 15 | — | — | 25 | — |
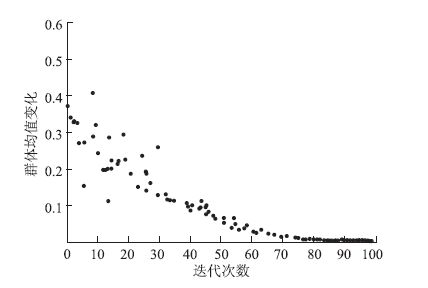
运用遗传算法求解,设种群规模为40,根据变量精度确定码长为10,以0.9为交叉率、0.06为变异率、压差2为目标函数来线性分配适应度值,经过100次迭代后输出结果。群体均值变化如图 3所示。
|
| 图 3 遗传算法运算迭代图 Fig. 3 Iterative graph of operation by genetic algorithm |
优化后所需车辆数和多层级常规公交运行时刻如表 3所示。
| 参数 | 线路 | |||||||
| I | II | III | IV | V | VI | VII | VIII | |
| 发车时刻 | 7:05 | 7:10 | 7:15 | 7:35 | 7:00 | 7:10 | 7:25 | 7:05 |
| 发车间隔/min | 2.5 | 5 | 5 | 5 | 10 | 10 | 10 | 20 |
| 所需车辆数/辆 | 30 | 15 | 14 | 13 | 5 | 4 | 5 | 2 |
优化前后公交企业运营车辆的投入和乘客等车费用变化情况如表 4所示。
| 对比项 | 优化前时刻表 | 优化后时刻表 | 变化率/% |
| 运营车辆数/辆 | 82 | 89 | +8.5 |
| 乘客换乘候车费用/元 | 2 200 | 1 782 | -23.5 |
从表 3可以看出,同层级多条线路在同一换乘站点向上一层级公交集散乘客,较低层级公交发车间隔与较高层级公交发车间隔的数值关系满足式(9),符合本文模型体系构建思想。由表 4中的对比数据可知,基于本文乘客与公交企业取相同权重值的假设,该模型对于提高换乘效率效果明显,虽然所需的公交车辆数增加,使企业的投入增加,但总体的系统费用得到了一定程度的改善。在公交调度中心做出调度决策时,应根据不同时段乘客与企业的相互关系,权衡之后决定乘客换乘候车成本和公交企业运营成本的权重。
6 结论本文基于到站时间差编制出权衡了公交乘客与公交运营企业利益的区域化多层级常规公交运行时刻表。通过算例分析,得出多层级常规公交区域协调运营时刻表,在降低公交乘客换乘候车费用的同时会增加公交车辆的投入,但系统总成本得到了改善,为进一步实现区域公交调度提供了理论基础。实际应用中,公交线路属性特征数据及行程时间会因不同时段的客流需求和不同交通条件有所变化,因此依据对应时段的数据重复采用上述模型和求解方法可制订出全天的公交网络运行时刻表。
| [1] | 邹毅,张瑾.安宁市城乡公交一体化规划研究[M].北京:人民交通出版社,2012. ZOU Yi, ZHANG Jin. Study on Integrated Planning of Anning Urban and Rural Public Transport[M].Beijing:China Communications Press,2012. |
| [2] | ADAMSKI A, CHMIEL W. Optimal Service Synchronization in Public Transport[C]//Transportation Systems 1997. Chania, Greece:[s.n.], 1997:1283-1287. |
| [3] | CEDER A, TAL O. Timetable Synchronization for Buses[C]//Computer-Aided Scheduling of Public Transport. Berlin:Springer-Verlag,1999. |
| [4] | FLEURENT C, LESSARD R, SÉGUIN L. Transit Timetable Synchronization:Evaluation and Optimization[C]//Proceedings of the 9th International Conference on Computer-aided Scheduling of Public Transport, San Diego:[s. n.], 2004:9-11. |
| [5] | 覃运梅.城市公交调度优化方法研究[D].合肥:合肥工业大学,2006. QIN Yun-mei. Research on Methods of City Bus Dispatching Optimization[D].Hefei:Hefei University of Technology, 2006. |
| [6] | 石琴,覃运梅,黄志鹏.公交区域调度的最大同步换乘模型[J].中国公路学报,2007,20(6):90-94. SHI Qin,QIN Yun-mei,HUANG Zhi-peng. Maximal Synchronous Transfer Model of Bus Regional Dispatching[J]. China Journal of Highway and Transport, 2007, 20(6):90-94. |
| [7] | 杨丽.基于换乘价值的城市公交区域调度方法研究[D].成都:西南交通大学,2010. YANG Li. Study of Bus Regional Scheduling Basd on Transfer Value[D].Chengdu:Southwest Jiaotong University, 2010. |
| [8] | 司徒炳强.公交网络时刻表编制的理论建模及可靠性控制方法研究[D]. 广州:华南理工大学,2011. SITU Bing-qiang. Research on Theoretical Modeling and Reliability Control Method of Timetable for Bus Network[D]. Guangzhou:South China University of Technology, 2011. |
| [9] | 陈霞.基于线网结构的公交协同研究[D].长沙:长沙理工大学,2011. CHEN Xia. Collaboration Based on Structure of Public Traffic Network[D]. Changsha:Changsha University of Science & Technology, 2011. |
| [10] | 何迪.公交发车时刻表区域协同模型研究[J].统计与决策,2012,8:56-58. HE Di. Study on Public Transportation Timetabling Regional Synchronized Model[J].Statistics and Decision,2012,8:56-58. |
| [11] | IBARRA-ROJAS O J, RIOS-SOLIS Y A. Synchronization of Bus Timetabling[J]. |
| [12] | 柏海舰,董瑞娟,张敏,等.基于同步多样性的公交时刻优化方法[J].交通运输工程学报,2013,13(3):79-85. BAI Hai-jian, DONG Rui-juan, ZHANG Min, et al. Optimization Method of Bus Time Based on Synchronization Diversity[J]. Journal of Traffic and Transportation Engineering, 2013, 13(3):79-85. |
| [13] | 熊杰,关伟,黄爱玲.社区公交接驳地铁路径优化研究[J].交通运输系统工程与信息,2014,14(1):166-173. XIONG Jie, GUAN Wei, HUANG Ai-ling. Research on Optimal Routing of Community Shuttle Connect Rail Transit Line[J]. Journal of Transportation Systems Engineering and Information Technology, 2014,14(1):166-173. |
| [14] | VUCHIC V R. 城市公共交通运营、规划与经济(上册:运营部分)[M]. 宋瑞,等译.北京:中国铁道出版社,2012. VUCHIC V R. Urban Transit:Operations, Planning, and Economics(Volume I:Operation)[M]. SONG Rui, et al translated. Beijing:China Railway Press, 2012. |
 2016, Vol. 33
2016, Vol. 33
