扩展功能
文章信息
- 蔡艳锋,孙大志,唐贵涛
- CAI Yan-feng, SUN Da-zhi, TANG Gui-tao
- 展宽段排队溢出状态下区段延误模型研究
- Study on Section Delay Model under Widening Zone Queue Overflow Condition
- 公路交通科技, 2016, Vol. 33 (6): 123-127
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 123-127
- 10.3969/j.issn.1002-0268.2016.06.020
-
文章历史
- 收稿日期:2015-10-08
2.昆明理工大学 交通工程学院,云南 昆明 650093
2. School of Traffic Engineering, Kunming University of Science and Technology, Kunming Yunnan 650093, China
信号交叉口是城市路网的重要组成部分,如何提高交通流在交叉口处的通行效率一直是城市交通管控的重点和难点。拓宽进口道可以增加进口道车道数并提高进口道的通行能力,其长度由展宽渐变段和展宽段构成[1]。红灯期间到达的车辆在展宽段内压缩存储,绿灯期间高效释放。早在1967年,Leisch[2]将进出口道拓宽部分相对于路段增加的车道称为短车道,并提出了若干短车道长度建议值;Lee[3]通过模拟手段分析了拓宽进口道的通行能力,但并未考虑溢出拥堵问题;Tian[4]、杨晓光[5]、程国柱[6]从概率论角度研究了展宽段长度受限下的交叉口通行能力。
延误是指行驶在路段上的车辆由于受到道路环境、交通管理与控制或其他车辆的干扰等影响而损失的时间[7]。现有延误模型多以整个进口道上的所有车辆为研究对象,较少对空间某路段通过车辆延误进行研究。随着展宽段的普遍设置,为了更好地发挥展宽段的功能,研究展宽段单周期内通过车辆所产生的区段延误极有必要。区段延误是指单位时间内通过某固定路段车辆所产生的延误。本文在3大经典延误理论的基础上,以整个展宽段为研究对象,在考虑展宽段最大排队长度和饱和流率波动的前提下,对展宽段排队溢出时所产生的区段延误进行分析研究。
1 经典延误模型多年来,国内外对交叉口延误的研究积累了丰富的成果,比较经典的理论方法有稳态理论、定数理论和过渡函数理论。
(1)稳态理论
稳态理论研究的是低饱和度稳态交通流延误时间和停车次数的数学表达式。车辆平均延误时间可以简化为均衡相位平均延误时间与随机平均延误时间两部分,较为经典的Webster延误模型[8]见式(1)、式(2)。另外,Miller和Akcelik也提出了相似的延误计算模型[9, 10]。
稳态理论总延误:
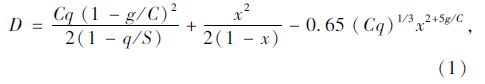
稳态理论平均延误:
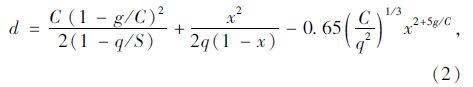
式中,D为总延误;d为平均延误;C为信号周期时长;q为车辆到达率;g为绿灯时长;S为饱和流率;x为饱和度。
稳态理论在低饱和度的情况下是比较切合实际的,但随着饱和度的增高,稳态理论计算结果与实际情况有较大出入,因此稳态理论不适用于计算过饱和状态下的延误。另外从式(1)、式(2)可以看出,稳态理论在计算延误时没有考虑研究路段的长度及饱和流率的波动问题。
(2)定数理论
定数理论是针对过饱和交叉口排队车辆随周期累积的现象提出的,其中典型的研究成果是May在1965年编著的《交通流理论》和其与Heller在1976年 合作编著的《定数排队模式》[11]。定数理论假设车辆到达率q大于通行能力Q,且在研究时段内为定值。定数理论把过饱和交通流作为一种确定的情况考虑,交通流排队长度、延误时间随时间线性增加。
定数理论总延误:

定数理论平均延误:
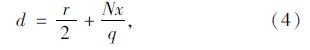
式中,r为红灯时长;N为平均滞留车辆数。
但定数理论同样没有考虑研究路段的长度及饱和流率的波动问题,因此计算出来的理论排队长度及延误时间是无限制的,这与本文要研究的展宽段内车辆周期区段延误相矛盾。
(3)过渡函数理论
过渡函数理论首先由Whiting提出,主要用于解决仿真程序中关于随机延误的模拟。后来,Kimber和Hollis深入研究了稳态理论与定数理论的结合方法,提出了过渡函数理论的推导模型[12]。
过渡函数总延误:
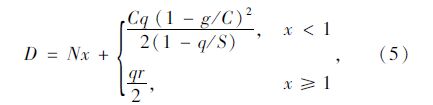
过渡函数平均延误:
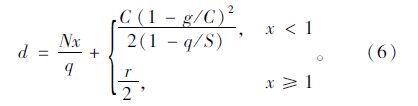
过渡函数理论的建立不仅解决了近饱和交通状态下车辆受阻滞程度的定量分析,而且弥补了过饱和交通状态下被定数理论所忽略的随机阻滞。但是同稳态理论和定数理论一样,过渡函数也没有考虑路段长度及饱和流率的波动问题,所以对过饱和状态下展宽段区段延误的计算不合适。
以上3种经典延误模型在计算信号交叉口延误时均没有考虑到路段的长度及饱和流率的波动问题,因此对于展宽段排队溢出状态下区段延误的计算结果将会与实际出现偏差。因此,本文以3种经典延误模型为基础,推导适合展宽段排队溢出状态的区段延误计算模型。
2 展宽段溢出状态下区段延误模型的建立本文以展宽段为研究对象,考虑在展宽段排队溢出时,单位周期通过展宽段车辆的区段总延误及车均延误。在这种情况下,展宽段内排队长度是固定的,不会像定数理论那样随着时间的延续一直增加。当绿灯启亮时,随着队首车辆的驶离,展宽段后排队车辆陆续进入展宽段。
为便于研究,现提出以下约定条件:
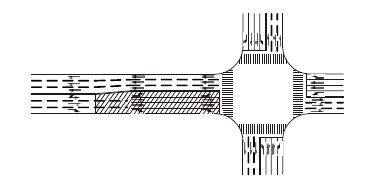
(1)以图 1所示交叉口为研究对象,各个方向设计参数相同,采用单口放行;
|
| 图 1 信号交叉口 Fig. 1 Signalized intersection |
(2)将展宽渐变段等同于展宽段进行分析,阴影部分为研究区域;
(3)西进口道由于过饱和引起排队溢出现象的发生;
(4)以排队溢出为研究起始点,展宽段内排队车辆车头间距取 ${\bar{h}}$;
(5)由于设有专用车道且不受信号控制,不对右转车辆进行研究。
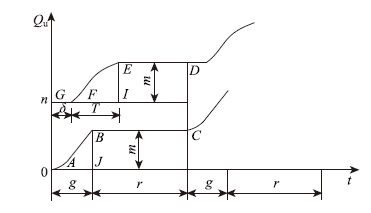
2.1 展宽段驶入流率qs和消散饱和流率S不恒定实际情况中,展宽段驶入流率qs和消散饱和流率S为变量。根据研究区段内交通流的特性,绘制出展宽段内单车道排队车辆数Qu与延误时间t的关系曲线,如图 2所示。
|
| 图 2 qs与S不恒定时的排队车辆数与延误时间< Fig. 2 Number of queuing vehicles and delay time when qs and S are unsteady |
图 2中,n为展宽段内单车道所能容纳的最大车辆数;δ为绿灯启亮后启动波传播至展宽段末端所用的时间;m为绿灯期间驶离展宽段的车辆数,也是后续驶入展宽段的车辆数;T为后续驶入展宽段m辆车所用的时间[13]。 求解单周期内单车道通过车辆的区段延误问题可以转化为求解不 规则图形ABCDEFG的面积问题,即为:
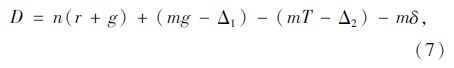
式中,D为单车道区间延误;Δ1为图形ABJ的面积;Δ2为图形IEF的面积。
2.2 展宽段驶入流率qs和消散饱和流率S恒定过饱和引起排队溢出的情况,单周期展宽段内车辆无法完全释放,释放车流流率经历了绿灯初期流率快速增长阶段和以饱和流率消散两个阶段。引入当量饱和流率Se的概念[14],将饱和流率转化为定值,计算公式为:
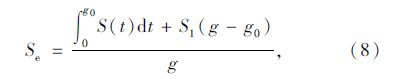
式中,Se为车流当量饱和流率;S(t)为绿灯初期车流流率随时间的变化函数;S1为车流饱和流率;g为相位有效绿灯时间;g0为绿灯初期流率增长阶段时长。
同样将展宽段车流驶入流率转化为定值,计算公式为:
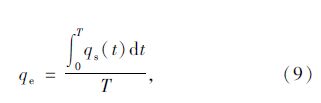
式中,qe为当量车流驶入流率;qs (t )为车流驶入流率随时间的变化函数。
从而绘制出展宽段驶入流率和消散饱和流率恒定时的排队车辆数Qu与延误时间t的关系曲线,如图 3所示。
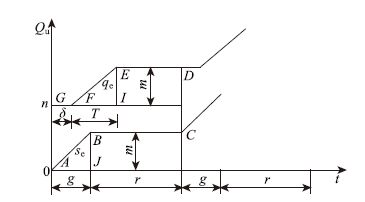
|
| 图 3 qs与S恒定时的排队车辆数与延误时间 Fig. 3 Number of queuing vehicles and delay time when qs and S are steady |
从而得出各参数的计算公式如下:





式中,L为拓宽进口道总长度;L1为展宽段长度;L2为展宽渐变段长度;${\bar{h}}$为排队车辆平均车头间距;u为进口道启动波波速。
这种情况下,单周期内单车道延误即可简化为:
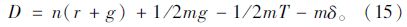
把式(10 )~ (14)代入式(15)得:
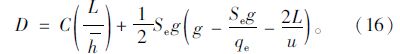
整个展宽段区段延误Dall的计算公式即为:
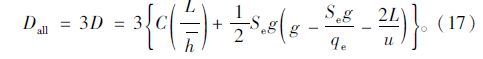
在一个信号周期内,展宽段内共进入与通过的车辆数为3 (n+m),所以车辆平均延误为:
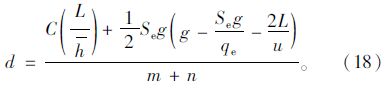
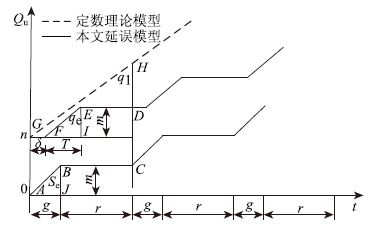
3大理论中,定数理论与本文研究模型的假设条件较为接近,为验证本文研究模型的优越性,以图 1所示交叉口为例,分别依照定数理论和本文提出的区段延误模型绘制单车道排队车辆数Qu与延误时间t随周期的变化趋势,如图 4所示。
|
| 图 4 定数理论与本文延误模型的比较 Fig. 4 Comparison of fixed number theory and proposed delay model |
假设展宽段后路段车流到达率恒定,从图 4可以看出,定数理论单车道延误即为不规则图形ABCHG的面积,定数理论每周期排队车辆数和车辆总延误随着周期的延续逐渐增加,而本文提出的区段延误模型所得的排队车辆数与车辆总延误在定值周围浮动。假设展宽段内单车道排队车辆数到达n辆排队溢出时为研究的第1周期,则利用定数理论计算的该周期总延误为:
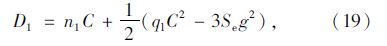
式中,n1=3n,ql为展宽段后路段车流到达率。
利用本文延误模型计算的总延误为:
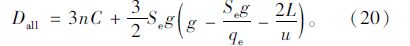
前者比后者多出的总延误为:
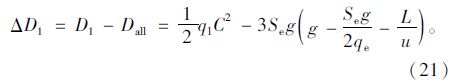
利用定数理论计算的第2周期总延误为:
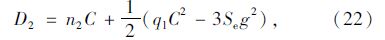
利用本文区段延误模型计算的总延误为:
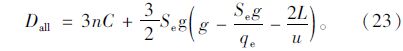
第2周期前者比后者多出的总延误为:
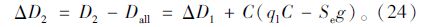
溢出车流消散之前的第i周期,定数理论比本文延误模型多出的总延误为:
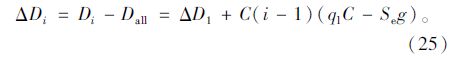
总延误增加量的斜率为:
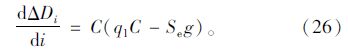
由以上计算过程可以得出,过饱和状态下定数理论计算出的总延误量与周期呈线性正相关,延误量增长速率与每周期内滞留的车辆数及信号周期有关,用定数理论延误模型计算出的总延误大于实际展宽段每周期通过车辆所产生的延误。相反,本文提出的展宽段区段延误模型能够很好地反映展宽段在排队溢出状态下进口道总延误和排队长度的特性。
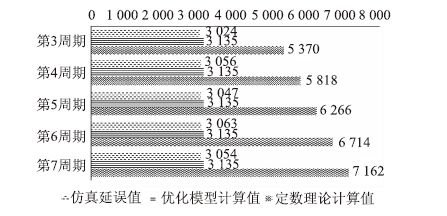
4 仿真验证以图 1所示交叉口为研究对象,应用VISSIM微观仿真软件进行区段延误模型的模拟验证,仿真界面如图 5所示。设该信号交叉口采用单口放行,各相位绿灯时长25 s,黄闪时长3 s,周期总计时长112 s,西进口路段车流到达率取1 200 veh/h,展宽段单车道车流驶入流率取1 500 veh/h,单车道车流消散饱和流率取1 600 veh/h,展宽渐变段长度为20 m,展宽段长度为60 m,车头间距取7 m,启动波波速取5 m/s,车流运行数据自第3周期开始检测。分别应用定数理论模型和本文区段延误模型进行单周期通过车辆总延误计算,并将计算结果与仿真所得区段总延误通过图表形式展现出来,具体如表 1和图 6所示。
|
| 图 5 VISSIM仿真界面 Fig. 5 VISSIM simulation interface |
| 第3周期 | 第4周期 | 第5周期 | 第6周期 | 第7周期 | |
| 仿真延误值/s | 3 024 | 3 056 | 3 047 | 3 063 | 3 054 |
| 优化模型计算值/s | 3 135 | 3 135 | 3 135 | 3 135 | 3 135 |
| 定数理论计算值/s | 5 370 | 5 818 | 6 266 | 6 714 | 7 162 |
|
| 图 6 三种所得延误值对比图(单位:s) Fig. 6 Contrast figure of 3 kinds of delay value(unit:s) |
由表 1和图 6可以看出,仿真延误值以3 049 s为中心上下轻微波动。总体来说,仿真延误值略小于区段延误模型计算值,较为稳定且不随周期的延续发生较大的波动。区段延误模型计算值为定值3 135 s,不随周期的延续而发生变化。定数理论计算值在第3周期起始已经大于仿真延误值和区段延误模型计算值,且随着周期的延续,定数理论计算值将以448 s为公差逐渐增加,直至无穷大。因此可以看出,与定数理论计算方法比较,本文提出的区段延误模型能够更好地反映信号交叉口单周期通过展宽段车辆的区段延误。
5 结论本文在定数理论的基础上,考虑展宽段长度和饱和流率的波动性,建立了展宽段排队溢出状态下的区段延误模型。该模型能较好地反映溢出状态下单周期通过展宽段车辆所产生的延误,为今后展宽段的科学设计提出参考依据。但模型的建立与研究过程中仍有一些不足之处,如未考虑右转车辆对直行和左转车辆的干扰以及右转车辆产生的延误。对常规四相位设置情况下区段延误模型的建立、区段延误模型与展宽段设置形式之间的内在逻辑关系均有待进一步的研究。
| [1] | GB 50647-2011, 城市道路交叉口规划规范[S]. GB 50647-2011, Code for Planning of Intersections on Urban Roads[S]. |
| [2] | LEISCH J E. Capacity Analysis Techniques for Design of Signalized Intersections:Installment No. 2 Part IV:High Type Facilities and Interchanges[J]. Public Roads, 1967, 34(10):171-210. |
| [3] | LEE J J. Impact of Lane Drops on Intersection Capacity[D]. North Caroline:North Carolina State University, 2005. |
| [4] | TIAN Z Z, WU N. Probabilistic Model for Signalized Intersection Capacity with a Short Right-turn Lane[J]. |
| [5] | 杨晓光, 赵靖, 曾滢, 等. 短车道对信号交叉口通行能力影响研究[J]. 公路交通科技, 2008, 25(12):151-156. YANG Xiao-guang, ZHAO Jing, ZENG Ying, et al. Research on Impact of Short Lane on Signalized Intersection Capacity[J]. Journal of Highway and Transportation Research and Development, 2008, 25(12):151-156. |
| [6] | 程国柱. 路口拓宽条件下信号交叉口通行能力研究[D]. 哈尔滨:哈尔滨工业大学, 2002. CHENG Guo-zhu. Research on Capacity of Widened Signalized Intersection[D]. Harbin:Harbin Institute of Technology, 2002. |
| [7] | 李江. 交通工程学[M]. 北京:人民交通出版社, 2002:66-67. LI Jiang. Traffic Engineering[M]. Beijing:China Communications Press, 2002:66-67. |
| [8] | WEBSTER F V. Traffic Signal Settings, Road Research Technical Paper No. 39[R]. London:Road Research Laboratory, 1958. |
| [9] | MILLER A J. Settings for Fixed-cycle Traffic Signals[J]. |
| [10] | AKCELIK R. Comments on the Application of Queueing Theory to Delays at Signals[J]. Australian Road Research, 1990, 20(3):53-61. |
| [11] | MAY A D, HELLER H E M. A Deterministic Queueing Model[J]. |
| [12] | KIMBER R M, HOLLIS E M. Peak Period Traffic Delays at Road Junctions and other Bottlenecks[J]. Traffic Engineering and Control, 1978, 19(10):442-446. |
| [13] | 刘岩, 王殿海. 基于短连线的过饱和信号交叉口最大延误模型[J].中国公路学报,2011,24(6):91-95. LIU Yan, WANG Dian-hai. Maximum Delay Model in Short Length Signalized Intersection under Supersaturated Traffic Flow[J]. China Journal of Highway and Transport, 2011, 24(6):91-95. |
| [14] | 尚斌. 基于信号交叉口渠化段长度的配时参数优化方法[D]. 长春:吉林大学, 2007. SHANG Bin. Optimal Method of Signal Parameters Based on Channelization Length at Signalized Intersections[D]. Changchun:Jilin University, 2007. |
 2016, Vol. 33
2016, Vol. 33
