扩展功能
文章信息
- 林 丽, 蒋 聪, 徐晓丹, 过宇亮, 陈 婷
- LIN Li, JIANG Cong, XU Xiao-dan, GUO Yu-liang, CHEN Ting
- 基于加速度干扰的城市隧道出入口交通流拥挤度评价
- Evaluation of Congestion Degree of Traffic Flow at Urban Tunnel Access Based on Acceleration Interference
- 公路交通科技, 2016, Vol. 33 (6): 113-118
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 113-118
- 10.3969/j.issn.1002-0268.2016.06.018
-
文章历史
- 收稿日期:2015-06-29
城市隧道在城市道路网中承担着重要的交通功能,其道路功能等级与城市快速路相似。然而在高峰时段,由于城市隧道出入口的衔接方式复杂,车辆驾驶行为不一致,出入口车辆的运行速度动态变化,致使该区域的交通流通行能力低于隧道内交通流,并易产生隧道交通流拥挤现象,无法保证交通流的快速通过。因此对城市隧道出入口交通流状态进行合理划分并对城市隧道服务水平提出科学的评价,有助于了解城市隧道交通流的运行状况和城市隧道的服务质量,同时为城市隧道出入口的组织设计、路况改善以及提高交通管理水平提供科学依据[1]。
衡量服务水平的主要指标有行车速度、行车时间、交通流密度、行车延误、驾驶员心理、乘客舒适度、行车安全性和运行费用等。交通流评价一般根据相应的服务水平指标,采用等级划分的方式来定性和定量地综合分析[2]。这种评价方式简单,结果直观,被相关学者广泛使用,但是其等级的界定主要采用经验法和模糊综合评判法,有一定的模糊性,无法直观反映微观车辆的运行动态,存在缺陷。因此,有必要完善交通流评价体系,寻求更加科学严密的服务水平评价指标来评价城市隧道出入口的交通流拥挤情况,并为工程实践提供参考。
1 加速度干扰现状评价 1.1 加速度干扰概述当车辆在城市隧道中行驶时,车速动态变化,无法保持某个绝对不变的速度行驶。当道路上的交通量较小时,车辆会在其所要求的速度左右摆动。当交通量较大时,跟驰现象明显,在隧道出口的交织区范围内,一旦受到车辆换道行为的影响,跟驰车辆的速度更会出现摆动。当车流量逐渐增大时,车辆之间的相互干扰增加,最直接的变化就是速度出现明显的波动,交通流状态从离散到拥挤,车流速度减小,交通流从拥挤到离散状态,车流又不断加速。加速度干扰σ就是用来描述车辆速度摆动的一个量化指标[3],该数值可以用来评价城市隧道出入口交通流中车辆之间的干扰程度。
1.2 加速度干扰研究现状Jones等对各类道路不同的交通条件及不同的驾驶员进行了加速度干扰的测量,其中,与拥挤评价相关的结论有:交通量增加,σ增加;由于停车、公交停靠站、横向交通等影响,增加了城市道路的交通拥挤,σ增加;与行驶时间和停车时间相比,σ值可能是交通拥挤更好的度量标准;σ的高值表明有潜在的危险情况[4]。文献[5]指出,建议将加速度干扰作为评价道路服务水平的指标。Winzer研究了在不同交通流密度下车辆的加速度干扰情况,指出当交通流密度增加时,σ值逐渐增大,然而在交通流密度继续增加到某个定值以后,σ值不再增加,而是开始逐渐降低。
国内学者很少对加速度干扰进行研究[6],最近几年,开始有相关文献通过加速度干扰指标来评价道路线形和行车舒适度[7, 8, 9],但只是建立了相关的模型,并没有构建相应完善的评价体系,通过加速度干扰值来衡量城市道路服务水平等级的研究资料也很少。总之,国内外对加速度干扰评价方面的研究均较少,国外已有的研究文献年代也比较久远,并没有成熟完善的研究成果。
2 加速度干扰的计算方法车辆速度摆动的大小可用加速度对平均加速度的标准差σ来表示,称σ为加速度干扰,单位与加速度的单位一致,其公式如下:

式中,T为观测总时间;a(t)为t时刻加速度;${\bar{a}}$为平均加速度。
如果加速度的观测以连续的时间间隔Δt来取样,那么相应的计算公式如下:
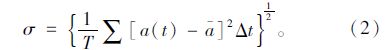
式(1)、式(2)本身对现场研究中所搜集的数据不能减轻计算工作。适用于数据简化和分析的加速度干扰方程为:
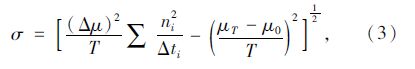
式中,Δμ为速度的等分间距;${{n}_{i}}=\frac{|{{\mu }_{i}}-{{\mu }_{i-1}}|}{\Delta \mu }$(取整数值),其中 |μi-μi-1| 为相邻两个时间间隔结束时速度差的绝对值;Δti为在速度数值niΔμ变化(n为整数)中的时间间隔;μT 为观测总时段的末速度;μ0为观测总时段的初速度;K为等加速度的路段数$\left( \sum\limits_{i=1}^{K}{\Delta {{t}_{i}}=T} \right)$。
3 加速度干扰特征分析 3.1 城市隧道出入口车速变化特性《公路隧道通风照明设计规范》(JTJ026.1—1999)[10]中根据照明亮度以及视觉适应性将隧道划分为5个不同路段,因此本文将城市隧道具体划分为:入口段、入口过渡段、中间段、出口过渡段和出口段,如图 1所示。

|
| 图 1 隧道分段示意图 Fig. 1 Schematic diagram of tunnel subsection |
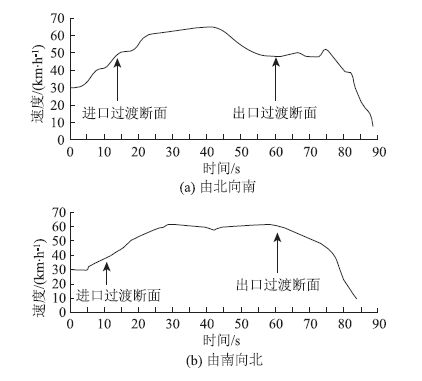
为获得城市隧道出入口车速变化的一般规律,研究城市隧道出入口交通流的加速度干扰特性,本文调查时间为工作日高峰小时时段(星期二至星期四16 :30—18 :30),在南京主城区的3个隧道(玄武湖隧道、鼓楼隧道和九华山隧道)中,利用试验车针对隧道交通流速度进行了跟车记录,见图 2至图 4,分析了各隧道出入口驾驶行为的变化对其后续车流车速造成的影响。

|
| 图 2 玄武湖隧道速度变化图 Fig. 2 Speed variation in Xuanwuhu tunnel |
|
| 图 3 鼓楼隧道速度变化图 Fig. 3 Speed variation in drum-tower tunnel |

|
| 图 4 九华山隧道速度变化图 Fig. 4 Speed variation in Jiuhuashan tunnel |
根据图 2至图 4,可以发现城市隧道出入口交通流的速度有如下特点:
(1)一般情况下,车辆在接近隧道入口过渡段时开始加速,而在接近出口过渡段时开始减速,出口处的车速低于进口处的速度。通过计算发现,前者加速度的绝对值小于后者。计算结果如下:3处隧道6个方向,隧道进口加速度均值为0.498 m/s2;出口加速度均值为-0.256 m/s2。该结果与高速公路隧道进出口车速变化[11]存在非常明显的差异,这是因为城市隧道出入口衔接着城市主干路或直接与平面信号交叉口相接,车流受到外部干扰较大,驾驶行为必然发生变化。以玄武湖隧道(由东向西)为例,距出口断面100 m处存在着平面信号交叉口,左转车流占60%以上,高峰时段交通流状态不稳定,由于前方车辆进入交叉口区域要发生减速换道,其换道波阵面沿着车流向后传播,致使车辆在接近出口过渡断面时,速度开始降低,并且降幅存在明显的波动。
(2)变坡对车辆加减速变化明显。隧道的出入口位置往往存在变坡点,以鼓楼隧道为例,其出入口的坡度在3条隧道中最大,其隧道出入口的变坡位置对应了出入口的过渡断面,因此,该位置前后驾驶员是否及时换挡将影响车辆的动力性能,并且驾驶员要适应隧道外部的交通条件(包括衔接城市道路和衔接平面信号交叉口)而采取相应的减速。
(3)平面线形对车辆的速度影响程度有限。由于城市隧道长度较短,九华山隧道2 780 km,玄武湖隧道2 660 km,鼓楼隧道1 150 km,隧道内部几乎为直线路段,平面线形对车速的影响并不明显。
3.2 加速度干扰值计算根据观测记录的数据,本节对3条城市隧道的车速进行加速度干扰的计算。以玄武湖隧道交通流车速为例,速度-时间轨迹见图 2。试验车开始以46 km/h的初始速度进入隧道,随后加速行驶,在30 s时,车速接近设计车速60 km/h,并以此速度小范围浮动行驶。在130 s时,由于接近出口过渡段,车辆被迫调整到较低速度行驶,车速降幅明显,记录的加速度干扰实测数据见表 1。
| 时间 间隔/s | 在每一时间间 隔结束时的经过时间/s | 在每一时间间 隔结束时的速度/ (km·h-1) | ni | Δti/s | $\frac{n_{i}^{2}}{\Delta {{t}_{i}}}/s$ |
| 0 | 0 | 46 | — | — | — |
| 1 | 10.3 | 46 | 0.00 | 10.3 | 0.00 |
| 2 | 12.0 | 45 | 1.00 | 1.7 | 0.59 |
| 3 | 13.4 | 47 | 2.00 | 1.4 | 2.86 |
| … | … | … | … | … | … |
| 40 | 183.2 | 32 | 2.00 | 4.4 | 0.91 |
| 41 | 184.2 | 25 | 7.00 | 1.0 | 49.00 |
| 42 | 185.5 | 20 | 5.00 | 1.3 | 19.23 |
| 总计 | — | — | — | 185.5 | 650.97 |
该案例中,进入隧道的初始速度μ0为46 km/h,离开隧道的末速度μT为20 km/h,在一般情况下,把1 s 作为计算σ值的统计时间间隔。从隧道出口过渡段开始,由于前方驾驶行为的变化,试验车速度出现明显波动,假设Δμ=1 km/h,将在每一时间间隔结束时的速度μ从km/h换算成m/s,利用式(3)计算得到σ值为:

通过试验车法,对城市隧道的交通流速度进行多次观测记录,分别得到交通流的σ值,见表 2。
| 名称 | 隧道 长度/m | 方向 | 隧道出口衔接 | 速度/ (km·h-1) | 饱和 度 | 加速度 干扰值/ (m·s-2) | |
| 玄武湖隧道 | 2 660 | 由东向西 | 平面信号交叉口 | 44.8 | 0.87 | 0.519 | |
| 由西向东 | 封闭的立交匝道 | 52.3 | 0.81 | 0.373 | |||
| 鼓楼隧道 | 1 152 | 由北向南 | 城市主干路 | 43.6 | 0.76 | 0.494 | |
| 由南向北 | 城市主干路 | 45.9 | 0.74 | 0.463 | |||
| 九华山隧道 | 2 780 | 由南向北 | 平面信号交叉口 | 45.6 | 0.88 | 0.600 | |
| 由北向南 | 封闭的立交匝道 | 58.0 | 0.78 | 0.239 |
上述调查试验是采用1辆试验车来得到σ值,未必能够代表大多数车辆的运行状况,并且在实际情况中,通过检测仪对车辆处于不同交通流状态的动态速度采集过程比较耗时费力,效率也较低。因此,为了更全面地反映出不同交通流状态下的车辆运行特征,计算出相应的σ值,从而判断交通流所处的状态,对道路服务水平进行分级。 本研究利用VISSIM模拟城市隧道单方向双车道道路环境,每隔0.01 s记录车辆的状态,同时根据所选的时空区域以1 s为统计时间间隔,计算车辆的σ值。图 5为通过VISSIM仿真得到的车辆正常行驶时加速度的波动图。将仿真值与实测数据进行验证后,认为该仿真可以用来分析车辆的加速度干扰特性。

|
| 图 5 正常行驶时车辆纵向加速度的波动图 Fig. 5 Vehicle longitudinal acceleration fluctuation during normal operation |
具体的仿真交通流状态(用饱和度表示)与σ值的关系见图 6。由图可知,该关系曲线上有几个关键的特征点:A,B,C,D。在OA阶段,随着饱和度的增加,σ值由低值逐渐变大,这主要是因为随着交通流状态由离散转化为 跟驰,车辆之间的相互干扰增大,需要通过不断调整车速来满足自身的期望车头间距,在该段曲线上就表现为σ值随着饱和度的增大而增加,直至达到最大值。

|
| 图 6 交通饱和度和加速度干扰关系 Fig. 6 Relation between traffic saturation and acceleration interference |
曲线过了A点之后,交通流状态是由跟驰转化为拥挤的过程,σ值不断下降,直至降低至一个较低的稳定值。这主要是因为随着交通量的增大,交通流越来越拥挤,车辆间的干扰也变得越来越大,车辆之间只存在车头间距变小,超车和换道变得越来越困难,车辆无法自由调整车速,故随着流量的增加,σ值逐渐变小。在整个AD区间中,AB阶段的曲线呈上凸趋势,σ值变化幅度不大,表明车辆在该阶段的相互干扰逐渐增大。然而有变换车道需求的驾驶员仍然可以寻找机会换道,如果驾驶员期望换道的频率较多,σ值就会偏大。在BC阶段,曲线斜率变化明显,开始下凹,σ值降低较为明显,说明车辆已经无法自由变换车道了。当交通量继续增加时,车辆之间的相互干扰也继续增加,几乎无法超车,整体车流的运行受到限制,只能跟车前进,车速的波动开始变小,从而使在CD阶段的σ值减至某较小值附近。当道路的通行能力低于交通流量时,交通流呈现拥堵状态,车辆停车排队,在极限情况下,σ值降至零。故根据图 6,将交通流状态划分为4个区域,各个区域之间有着各自相对应的车辆运行特征。
4 基于加速度干扰的服务水平划分 4.1 基于加速度干扰的现状交通流状态评价σ值主要受驾驶员、道路和交通情况3种因素的影响。在高峰时段,交通情况对σ值的影响大于前两者,因此,根据表 2计算的结果,本文主要分析交通环境的变化与σ的关系,发现有如下特点:
(1)当城市隧道出口衔接大型平面信号交叉口时,隧道内的跟驰 车流被迫调整到较低速度来适应隧道外部环境的变化,包括换道、超车甚至停车排队等。这些驾驶行为使跟驰车流车速受到较大的干扰,加速度干扰值超过0.5 m/s2,发生拥挤的概率最大。
(2)当城市隧道出口衔接封闭的道路(如立交匝道)时,隧道车流车速受到外界干扰较小。车辆从出口过渡段到离开洞口的过程存在一个完整封闭的过渡区,因此发生换道、超车等驾驶行为的情形相对较少,从而对隧道交通流的加速度干扰最小,发生拥挤的概率也最小。
(3)当城市隧道出口衔接城市主干路时,隧道跟驰车流的车速受到的干扰程度介于上述两种情形之间。这主要是因为隧道内的跟驰车流通过出口断面后汇入城市主干路,隧道口的跟驰车流受到的干扰主要来自于隧道外平面车流的横向干扰,干扰程度有限。另外,当车辆驶出隧道,驶入城市道路,不久就会进入平面交叉口区域,出现车速降低甚至停车排队的现象在所难免,从而产生波阵面,波速沿着跟驰车流向后传播,传至隧道出口断面时,交通波的波速已变小,从而使隧道交通流受到的加速度干扰较小,降低了发生拥挤的概率。
(4)鼓楼隧道全长最短,车辆从入口行驶到出口离开的整个过程中,由于变坡、照明等因素,车辆的车速始终在不断变化调整,导致加速度整体波动偏大。
4.2 基于加速度干扰的服务水平划分标准由图 6呈现的曲线特征可知,4个阶段的车辆运行特征存在着明显差异,对应的σ值变化特性也有所区别。由于城市隧道的设计速度为60 km/h,因此,参考《城市道路工程设计规范》(CJJ37—2012)[12]中快速路的服务水平分级,并综合考虑交通流的速度、饱和度等指标,基于σ值,将城市隧道单向交通流的服务水平分成4个等级,见表 3。
| 服务水平等级 | 加速度干扰/(m·s-2) | 速度/ (km·h-1) | 饱和度 | 最大服务交通量/ (pcu·h-1) | |
| 一级(自由流) | ≤0.5 | ≥65 | 0.30 | 600 | |
| 二级(稳定流上段) | <0.5 | ≥50 | 0.55 | 1 000 | |
| ≥0.4 | |||||
| 三级(稳定流) | <0.4 | ≥44 | 0.77 | 1 500 | |
| ≥0.2 | |||||
| 四级 | (饱和流) | >0.5 | ≥30 | ≈1.00 | 1 800 |
| (强制流) | <0.2 | <30 | >1 | — | |
表 3的划分标准与图 6呈现的特征是一致的。当服务水平较高时,车速较快,交通流处于离散状态,车流之间的相互干扰少,σ值较低;当交通流的饱和度逐渐变大时,车流之间的干扰增多,此时,驾驶员为寻求期望的车头间距而频繁调整车速,σ值就逐渐提高;当道路中的交通量仍在持续增多时,车流运行时受到的阻碍也开始逐渐增加,车速的波动幅度越来越小,因此,σ值开始降低;当道路呈现拥挤状态时,饱和度接近1,车辆行驶缓慢,车速变化受到的限制达到最大,此时车速几乎无法改变,σ值也降至最低。因此,车流的σ值可以体现出不同的道路服务水平。
由表 3的划分标准也可以看出,在同一等级交通流状态的评价指标中,只有σ值同时出现两种分级标准,这是由于同一个σ值可能会表示出完全不同的两种交通流状态。例如,当服务水平为四级,交通流处于强制流状态时,车辆几乎处于停滞状态,因此车辆之间便难以再产生干扰,此时,σ值小于0.2 m/s2;然而当服务水平为一级,交通流处于自由流状态时,车流密度小,车速较高,相互干扰小,σ值也非常有可能小于0.2 m/s2,因此,在利用σ值进行服务水平划分时,参考速度、饱和度以及最大服务交通量等指标的分析,能够更全面地呈现出基于σ值的服务水平评价方法的特点。
5 结论阐述了加速度干扰用于道路服务水平评价的实践意义,介绍了加速度干扰的计算方法,利用实测和仿真数据,得到了城市隧道交通流σ值的关系图,根据该图表现出来的不同车辆运行特征,可以将城市隧道单行双车道服务水平分为4个等级,并相应给出了各级之间平均速度的取值范围。通过对不同隧道交通流σ值的计算分析,发现城市隧道出入口衔接类型与城市隧道交通流内部干扰程度密切相关,并指出短距离隧道对交通流车速的波动影响明显。
σ值是对车辆之间相互干扰程度的一个量化指标,它衡量了车流在不同状态下的相互影响度,并且能够从加速度干扰的变化趋势上划分出交通流随流量变化的内在特性,因此将σ值作为划分道路服务水平的标准具有现实意义,但是利用σ值评价仍然存在着不足:变化的趋势图中有转折点,在该值附近具有两种不同的交通流状态,故在实际情况评价时,必须将速度、饱和度等其他评价指标与σ值相结合,进行综合分析,对道路服务水平提出更完善的评判标准。
| [1] | 李相勇, 蒋葛夫. 城市道路服务水平的模糊综合评判[J]. 交通运输系统工程与信息, 2002, 2(3):48-50. LI Xiang-yong, JIANG Ge-fu. Fuzzy Comprehensive Assessment of Service Level for Urban Roads[J]. Journal of Transportation Systems Engineering and Information Technology,2002, 2(3):48-50. |
| [2] | 任福田. 新编交通工程学导论[M].北京:中国建筑工业出版社,2011. REN Fu-tian. Introduction to New Traffic Engineering[M]. Beijing:China Building Industry Press, 2011. |
| [3] | 鸠洛夫D L, 休伯M J. 交通流理论[M]. 蒋璜, 等译. 北京:人民交通出版社,1983. DOVEROVE D L, HUBER M J. Traffic Flow Theory[M]. JIANG Huang, et al translated. Beijing:China Communi-cations Press, 1983. |
| [4] | JONES T R, POTTS R B. The Measurement of Acceleration Noise:A Traffic Parameter[J]. |
| [5] | DREW D R, DUDEK C L, KEESE C J. Freeway Level of Service as Described by an Energy-acceleration Noise Model[R]. Washington, D. C.:National Research Council, 1967:30-85. |
| [6] | 刘江.基于加速度干扰的双车道公路服务水平量化研究[J]. 土木工程学报,2012,45(10):169-174. LIU Jiang. Quantitative Research on Level-of-service of Two-lane Highways Based on Acceleration Noise[J]. Journal of Civil Engineering, 2012, 45(10):169-174. |
| [7] | 许伦辉, 周静. 基于道路结构的加速度干扰模型及行车安全舒适性评价[J]. 公路, 2007(3):102-107. XU Lun-hui, ZHOU Jing. Acceleration Noise Model Based on Road Structure and Evaluation of Traffic Safety and Riding Comfort[J]. Highway, 2007(3):102-107. |
| [8] | 李林, 徐建闽, 叶凡. 基于道路平面线形的加速度干扰模型研究[J]. 中外公路, 2010, 30(2):18-21. LI Lin, XU Jian-min, YE Fan. Research on Acceleration Interference Model Based on Road Plane Alignment[J]. Journal of China & Foreign Highway, 2010, 30(2):18-21. |
| [9] | 黄艳国, 康裕荣, 许伦辉. 基于道路线形的加速度干扰与行车舒适性分析[J]. 中外公路,2011,31(3):287-290. HUANG Yan-guo, KANG Yu-rong, XU Lun-hui. Analysis of Acceleration Disturbance and Driving Comfort Based on Road Alignment[J]. Journal of China & Foreign Highway, 2011, 31(3):287-290. |
| [10] | JTJ026.1-1999,公路隧道通风照明设计规范[S]. JTJ026.1-1999,Specifications for Design of Ventilation and Lighting of Highway Tunnel[S]. |
| [11] | 杨轸, 郭忠印. 隧道进出口车速变化研究[J].上海公路,2006(1):48-51. YANG Zhen, GUO Zhong-yin. Research on Speed Alteration at Entrance and Exit of Tunnel[J]. Shanghai Highways, 2006(1):48-51. |
| [12] | CJJ37-2012, 城市道路工程设计规范[S]. CJJ37-2012, Code for Design of Urban Road Engineering[S]. |
 2016, Vol. 33
2016, Vol. 33
