扩展功能
文章信息
- 刘 云,张惠珍
- LIU Yun, ZHANG Hui-zhen
- 多目标带时间窗的车辆路径问题的单亲遗传混合蚁群算法
- A Partheno-genetic Hybrid Ant Colony Algorithm for Solving Multi-objective Vehicle Routing Problem with Time Window
- 公路交通科技, 2016, Vol. 33 (6): 95-100,106
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 95-100,106
- 10.3969/j.issn.1002-0268.2016.06.015
-
文章历史
- 收稿日期:2015-08-20
带时间窗的车辆路径问题[1](Vehicle Routing Problem with Time Windows,VRPTW)最早由Savelsbergh提出,是在车辆路径问题(Vehicle Routing Problem,VRP)的基础上增加了客户接受配送服务的时间窗要求,较VRP更贴近实际生活。VRPTW已被证实是一个NP难问题,当问题规模较大时,精确算法难以求出其最优解,因此,国内外很多学者利用智能启发式算法来寻找其满意解。常见的求解VRPTW的智能启发式算法有遗传算法[2, 3]、蚁群算法[4, 5, 6, 7]、模拟退火算法[8, 9]、粒子群算法[10, 11]等。然而,迄今为止,这些智能启发式算法大都被用于求解单目标的车辆路径问题,在多目标车辆路径优化问题中涉及的并不多。随着电子商务的迅速发展,物流配送任务日益庞大和复杂,追逐单一目标最优已经无法满足商家的发展要求,因此研究多目标的车辆路径问题迫在眉睫。
多目标车辆路径问题是指:给定若干具有一定需求量的客户,若干具有一定装载能力的车辆从配送中心出发,为客户进行配送服务后回到配送中心,同时使总路程最短、车辆数最少、费用最省等多个目标达到最优。与带时间窗的单目标车辆路径问题相比,多目标车辆路径问题更接近于现实生活,对实际问题更有指导意义。本文所研究的多目标VRPTW不仅要求完成配送任务的总路程最短和车辆数最少,而且车辆在配送过程中的等待时间和运输时间不能超过一定限制,本文将该问题称之为“具有最大等待时间和运输时间限制的多目标带时间窗的车辆路径问题”。
单亲遗传算法[12](Partheno-Genetic Algorithm,PGA)取消了传统遗传算法(Genetic Algorithm,GA)中的交叉算子,仅需一个父代,因此即使种群中的个体均相同,也不会影响遗传操作,降低了对种群多样性的要求。此外,单亲遗传算法在寻优效率和“早熟收敛”上都较传统遗传算法具有优势[13]。而蚁群算法(Ant Colony Algorithm,ACA)具有鲁棒性强、可以进行分布式计算,易与其他算法有效结合等优点,但其容易陷入局部最优。本文针对具有最大等待时间、最大运输时间限制的多目标带时间窗的车辆路径问题,在单亲遗传算法和蚁群算法的基础上,吸收这两种方法的长处和优势,克服它们的短处和缺陷,进而提出混合型搜索多目标车辆路径问题的启发式优化算法,并通过测试算例验证其求解性能。
1 具有最大等待时间和运输时间限制的多目标VRPTW 1.1 问题描述本文研究的是总路程和车辆数均受限的多目标VRPTW,该问题不仅要求配送车辆完成配送任务所行驶的总路程最短,而且要求在总路程最短的基础上完成任务所使用的车辆数最少。假设所有车辆都相同且容量相等,所探讨的问题也必须同时要满足如下条件:
(1)服务约束:每辆车可以服务多个客户,但一个客户只能由一辆车服务。
(2)配送中心约束:所有车辆由单一配送中心出发,配送完路径上所有的客户后返回到配送中心。
(3)装载量约束:每条路径上所有客户的需求量之和不能超过车辆的最大载重量WE。
(4)最大运输时间约束:每辆车的运输时间(行驶时间、服务时间以及等待时间之和)不能超过最大运输时间T。
(5)时间窗约束:客户i接受服务的时间不能超过其时间窗 [ei,li ]的限制。其中,ei为客户i最早接受服务的时间,li为其最晚接受服务的时间。
(6)最大等待时间约束:车辆给任一客户配送货物时的等待时间不能超过W,车辆若早于客户最早服务时间ei到达,则需等待一段时间,等待时间过长会影响车辆的配送效率,增加企业成本。
1.2 符号定义与数学模型下面对具有最大等待时间和运输时间限制的多目标带时间窗的车辆路径问题建立数学模型。
已知一个配送中心(配送中心用1表示)和N个客户(i=1,2,…,N),设总的车辆数为K;每辆车的最大载重量和最大工作时间分别为WE和T;车辆到达客户i的时刻为ti;客户i允许服务的最早开始时间和最晚开始时间分别为ei和li;客户i的需求量、服务时间和等待时间分别为di,si和wi(有上限);wj为客户j的等待时间;客户i到客户j的距离为cij;车辆从客户i到客户j所需要的行驶时间为tij,|S|为某一车辆的配送客户集,S 表示集合S中所含的顶点个数。
决策变量:

数学模型:

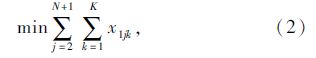

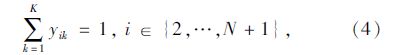
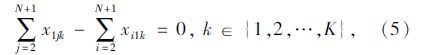
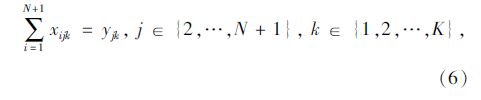

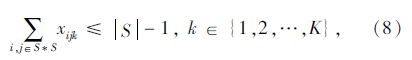
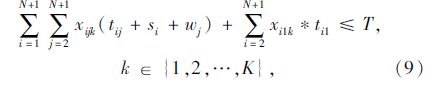
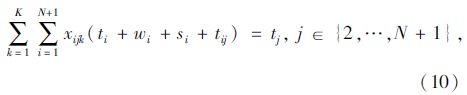
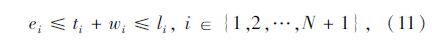
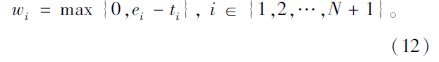
模型中,式(1)和式(2)分别为要求总路程和车辆数最少的目标函数;式(3)为车辆载重量限制;式(4)表示每一个客户只能由一辆车服务;式(5)表示从配送中心出发的车辆在完成配送任务后要返回配送中心;式(6)表示车辆在服务完客户i后紧接着服务客户j;式(7)表示车辆在服务完客户j之前只服务客户i;式(8)表示消除子回路,式(6)~式(8)共同形成可行回路;式(9)为车辆运行时间限制;式(10)为到达每个客户的时间表达式;式(11)为时间窗限制;式(12)为等待时间表达式。
2 单亲遗传混合蚁群算法的设计 2.1 单亲遗传算法单亲遗传算法的遗传算子包括基因重组算子和基因突变算子。基因重组算子又可分为基因换位算子、基因移位算子以及基因倒位算子。单亲遗传算法所有的遗传 操作都可分为单点基因操作和多点基因操作。本文所用的遗传算子为单、多点基因换位算子和单、多点基因移位算子,现分别介绍如下:
(1)基因换位算子
基因换位是指交换一条染色体中某两个(些)基因的位置[14],被交换的基因位置随机生成。
单点基因换位:


基因移位是指将一条染色体中某个(些)子串中基因的位置依次后移,并把该子串中的最后一个基因移到最前面的位置[14],子串长度随机生成。
单点基因移位:

多点基因移位:

蚁群算法是意大利学者M.Dorigo等人通过模拟蚁群觅食行为提出的一种基于种群的模拟进化算法。蚁群算法采用分布式并行计算机制,易与其他方法结合,具有较强的鲁棒性等特点。但该算法亦有搜索时间较长,易陷入局部最优的缺点。路径上信息素的更新和蚂蚁状态的转移是蚁群算法的重要组成部分。本文针对基本蚁群算法收敛速度慢和易陷入局部最优等缺点,蚂蚁的状态转移规则采用了确定性选择和伪随机比例选择相结合的方法,以便有效抑制算法的早熟现象,并加快算法的求解速度。
2.2.1 信息素更新规则本文利用式(13)~(15)对客户i和客户j路径上的信息素进行更新:
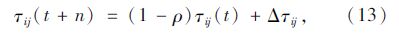
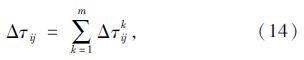

式中,τij(t+n)为所有蚂蚁完成一次周游,n只蚂蚁通过边(i,j)后,边(i,j)的信息素含量;ρ(0<ρ<1)为信息素挥发系数;Δτij为边(i,j)上信息素的增量;Δτijk为蚂蚁k在边(i,j)上留下的单位长度信息素增量;Q为信息素强度;L(k)为第k只蚂蚁在本次周游中所走的路径长度。
2.2.2 状态转移规则本文采用了确定性选择和伪随机比例选择相结合的方法确定蚂蚁的状态转移,即当蚂蚁位于客户i时,会以概率q0使用确定性选择规则或以概率1-q0 使用伪随机比例选择规则(pseudo random proportional action choice rule)选择下一个客户j。
确定性选择规则:
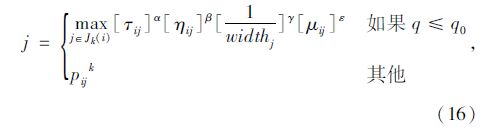
伪随机比例规则:
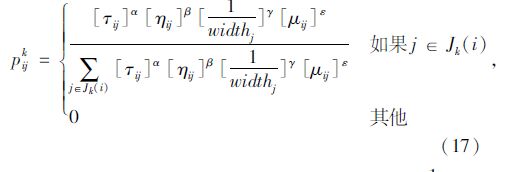
式中,τij为边(i,j)上的信息素浓度;${{\eta }_{ij}}=\frac{1}{{{d}_{ij}}},{{d}_{ij}}$为边(i,j)的长度,反映了蚂蚁对下一个客户的预见性; $\frac{1}{widt{{h}_{j}}}\left( widt{{h}_{j}}={{l}_{j}}-{{e}_{j}} \right)$是客户j的时间窗紧度,当j1和j2都是候选客户时,若j1的时间窗跨度比j2的小,选择客户j1时可以提高车辆的配送效率;μij (μij=d1i+di1+d1j+dj1-(d1i+dij+dj1)=di1+d1j-dij)为将客户点i和客户点j直接连接和两点分别与配送中心连接产生的节约量;α,β,γ,ε为权衡因子,分别决定了信息素浓度τij与启发式信息ηij,$\left[ \frac{1}{widt{{h}_{j}}} \right]$和μij的相对影响力;q0∈(0,1)是一个常数;q为(0,1)区间的随机数;Jk (i)为对于蚂蚁k位于客户i时可选择客户的集合;pijk为当蚂蚁k位于客户i时,离蚂蚁k越近、时间窗紧度越小、节约量越大、信息素浓度越大的客户j越容易被选择。
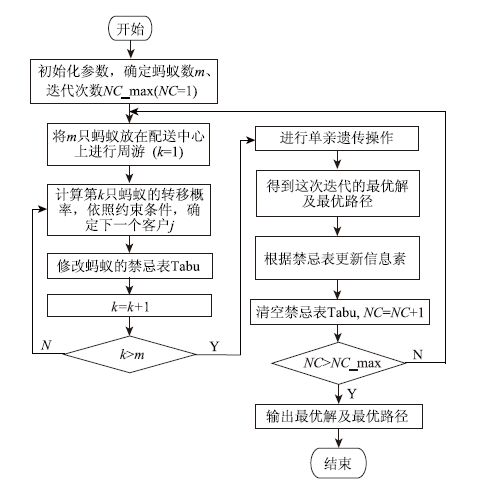
2.3 单亲遗传混合蚁群算法的步骤将单亲遗传算法和蚁群算法相融合,本文构建了求解多目标车辆路径问题(1 )~ (12)的单亲遗传混合蚁群算法,其算法框图如图 1所示。
|
| 图 1 算法流程图 Fig. 1 Flowchart of algorithm |
单亲遗传混合蚁群算法的优化步骤如下:
步骤1:初始化各参数,确定蚂蚁数m和最大迭代次数NC_max。
步骤2:m只蚂蚁从配送中心出发。对于蚂蚁k,按照式(16 )、 (17)计算其转移概率,确定下一个服务的客户j,若客户j满足载重量(3)、车辆运行时间(9)、 时间窗(11)、等待时间(12)等约束条件,则将客户j加入蚂蚁k的禁忌表中;否则,车辆回到配送中心,并重新启动下一辆车执行未完成的配送任务。
步骤3:所有客户服务结束后,蚂蚁完成一次周游,此时得到问题的一个可行解。更新蚂蚁数k=k+1,若k≤m,转步骤2;否则,转步骤4。
步骤4:从m只蚂蚁的禁忌表中选出最优路径,并对其进行单亲遗传操作(采用不同的基因移位、基因换位操作,即可产生不同的单亲遗传混合蚁群算法),即将该最优解路径 A 看成一个染色体,按一定的概率q对其作移位或换位变换,生成一条新路径 B 。
步骤5:若路径 B 的目标 函数值优于路径 A 的目标函数值,则更新最优路径和最优解,同时将禁忌表中路径 A 更新为路径 B ,以新的禁忌表更新信息素;否则,最优路径、最优解、禁忌表保持不变。
步骤6:根据信息素更新规则,式(13 )~ (15)对信息素进行更新,并清空禁忌表。更新迭代次数NC=NC+1 ,若NC≤NC_max,转步骤2。
步骤7:输出当前最优解和最优路径。
3 实例计算为了测试算法的计算性能,本文利用基本蚁群算法、单点单亲遗传混合蚁群算法和多点单亲遗传混合蚁群算法对文献[15]中的测试算例进行求解,并对比分析各种算法的求解效率与精度。
测试算例中各参数设定情况如下:利用最大载重量WE为8 t的最少车辆向20个客户(客户数据如表 1所示)提供配送服务,每辆车的最大运行时间T为8 h,车辆等待时间wi上限为4.5 h(为避免初次迭代时无法确定第一个客户,故等待时间上限为客户中最迟的时间窗开始时刻,即为客户编号10的时间窗开始时刻4.5 h),车辆的运行速度v保持恒定为40 km/h。配送中心坐标位置为(70 km,70 km),配送中心的需求量、服务时间、时间窗均为0。
| 客户 编号 | 横坐标/ km | 纵坐标/ km | 需求量/ t | 服务 时间/h | 时间窗开始 时刻/h | 时间窗结束时刻/h |
| 1 | 70 | 70 | 0 | 0 | 0 | 0 |
| 2 | 107 | 77 | 3.4 | 0.2 | 1.5 | 3.5 |
| 3 | 109 | 139 | 0.8 | 0.2 | 3.0 | 5.5 |
| 4 | 120 | 22 | 3.9 | 0.2 | 2.0 | 5.0 |
| 5 | 48 | 47 | 1.9 | 0.4 | 1.5 | 5.0 |
| 6 | 116 | 22 | 3.2 | 0.2 | 2.0 | 5.5 |
| 7 | 12 | 138 | 1.4 | 0.5 | 4.0 | 8.0 |
| 8 | 86 | 40 | 2.2 | 0.4 | 1.5 | 3.0 |
| 9 | 121 | 124 | 2.1 | 0.2 | 2.5 | 5.0 |
| 10 | 61 | 57 | 3.5 | 0.2 | 4.5 | 8.0 |
| 11 | 40 | 113 | 2.3 | 0.2 | 2.0 | 3.5 |
| 12 | 129 | 24 | 1.8 | 0.4 | 2.5 | 5.5 |
| 13 | 12 | 84 | 1.6 | 0.4 | 2.0 | 4.5 |
| 14 | 44 | 116 | 2.7 | 0.2 | 3.0 | 6.0 |
| 15 | 102 | 52 | 1.5 | 0.2 | 3.5 | 5.5 |
| 16 | 41 | 36 | 1.3 | 0.2 | 4.0 | 7.0 |
| 17 | 132 | 138 | 2.4 | 0.4 | 3.0 | 6.0 |
| 18 | 104 | 139 | 2.9 | 0.2 | 3.0 | 5.0 |
| 19 | 104 | 54 | 1.3 | 0.4 | 1.0 | 3.5 |
| 20 | 22 | 104 | 1.1 | 0.4 | 2.0 | 4.5 |
| 21 | 46 | 133 | 0.7 | 0.4 | 2.0 | 4.5 |
本文利用MATLAB R2011a 对基本蚁群算法、单点单亲遗传混合蚁群算法和多点单亲混合蚁群算法进行编程实现,3种算法在 Intel Core i3-2310M 2.10 GHz (6.00GB RAM),操作系统为Win7的环境下运行。为便于比较,3种算法中各参数设定相同的数值,参数设定情况为:蚂蚁数m=20,最大迭代次数NC_max=200,信息素挥发系数ρ=0.1,信息素强度Q= 15,信息素因子α=1,显著性因子β=1,时间窗紧度因子γ=2,节约量因子ε= 3,转移概率q0=0.6,换位算子概率q=0.7。
3种算法随机运行25次,优化结果如表 2所示。基本蚁群算法求出的最优路径长度为1201.923km,最优车辆数为8辆,算法运行平均耗时为65.84s;单点单亲遗传混合蚁群算法求出的最优路径长度为1157.415km,最优车辆数为7辆,算法运行平均耗时为56.25s;多点单亲遗传混合蚁群算法求出的最优路径长度为1189.409km,最优车辆数为7辆,算法运行平均耗时为57.63s。可见,单点单亲遗传混合蚁群算法与多点单亲遗传混合蚁群算法具有较高的求解效率,其求得的解均优于基本蚁群算法求得的解,并且单点单亲遗传混合蚁群算法的求解性能更优于多点单亲遗传混合蚁群算法。
| 算法 | 基本蚁群算法 |
单点单亲遗传 混合蚁群算法 |
多点单亲遗传 混合蚁群算法 |
| 最优路径长度/km | 1 201.923 | 1 157.415 | 1 189.409 |
| 最优车辆数/veh | 8 | 7 | 7 |
| 最差路径长度/km | 1 312.641 | 1 202.840 | 1 245.408 |
| 最差车辆数/veh | 9 | 8 | 8 |
| 平均路径长度/km | 1 268.976 | 1 187.228 | 1 219.152 |
| 平均车辆数/veh | 8.02 | 7.36 | 7.48 |
| 平均耗时/s | 65.84 | 56.25 | 57.63 |
经过多次测试运算发现,单点单亲遗传混合蚁群算法在其他参数保持不变的情况下,改变转移概率q0的取值,计算结果能够得到进一步优化。当q0=0.4时,随机运行单点单亲遗传混合蚁群算法10次所得的车辆数均为7,路径长度的标准差为16.435 km。较低的标准差说明单点单亲遗传混合蚁群算法具有较好的稳定性。
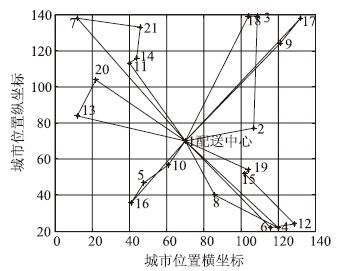
单点单亲遗传混合蚁群算法10次运行结果的最优路径长度为1095.510 km,车辆数为7辆,最优配送方案的路线图如图 2所示(1代表配送中心,2-21代表 20个客户的编号)。7辆车的配送路线分别为:
|
| 图 2 最优配送方案路径图(单位:km) Fig. 2 Routes of optimal delivery scheme(unit:km) |
车辆1:1-8-4-1;
车辆2:1-16-5-10-1;
车辆3: 1-2-3-18-1;
车辆4: 1-19-15-12-6-1;
车辆5: 1-11-14-21-7-1;
车辆6: 1-20-13-1;
车辆7: 1-9-17-1。
4 结论本文对具有最大等待时间和运输时间限制的多目标带时间窗的车辆路径问题建立了数学模型,然后针对该问题,将单亲遗传算法与蚁群算法相结合,使两种算法相互取长补短,设计出求解多目标车辆路径问题的单亲遗传混合蚁群算法。求解测试算例表明:在基本蚁群算法中引入单亲遗传算子操作后,能够有效改善基本蚁群算法收敛速度慢和易陷入局部最优的缺点。本文所设计的单亲遗传混合蚁群算法不仅具有较好的求解性能,而且能够有效求解多目标带时间窗的车辆路径问题,尤其单点单亲遗传混合蚁群算法具有较高的计算效率和较高的稳定性,是求解多目标带时间窗的车辆路径问题的一种有效算法。
本文所提出的单亲遗传混合蚁群算法不仅为多目标车辆路径问题的求解提供了一种较为有效的工具和手段,而且本文研究内容也拓宽了蚁群算法的改进方法。
| [1] | SAVELSBERGH M W P. Local Search in Routing Problems with Time Windows[J]. |
| [2] | URSANI Z, ESSAM D, CORNFORTH D, et al. Localized Genetic Algorithm for Vehicle Routing Problem with Time Windows[J]. |
| [3] | GHOSEIRI K, GHANNADPOUR S F. Multi-objective Vehicle Routing Problem with Time Windows Using Goal Programming and Genetic Algorithm[J]. |
| [4] | DING Q L,HU X P, SUN L J, et al. An Improved Ant Colony Optimization and Its Application to Vehicle Routing Problem with Time Windows[J]. Neurocomputing, 2012,98(12):101-107. |
| [5] | 张勇. 基于改进蚁群算法物流配送路径优化的研究[J]. 控制工程, 2015, 22(2):252-256. ZHANG Yong. Study of Optimizing Logistic Distribution Routing Based on Improved Ant Colony Algorithm[J]. Control Engineering of China, 2015, 22(2):252-256. |
| [6] | 何小锋,马良.带时间窗车辆路径问题的量子蚁群算法[J]. 系统工程理论与实践,2013, 33(5):1255-1261. HE Xiao-feng, MA Liang. Quantum-inspired Ant Colony Algorithm for Vehicle Routing Problem with Time Windows[J]. Systems Engineering-Theory & Practice, 2013, 33(5):1255-1261. |
| [7] | 温惠英,徐建闽.基于改进型蚁群算法的车辆导航路径规划研究[J]. 公路交通科技,2009,26(1):125-129. WEN Hui-ying, XU Jian-min. Research on Vehicle Routing Problem Based on Improved Ant Colony Algorithm[J]. Journal of Highway and Transportation Research and Development, 2009, 26(1):125-129. |
| [8] | 王超,穆东. 基于模拟退火算法求解VRPSPDTW问题[J]. 系统仿真学报, 2014, 26(11):2618-2623. WANG Chao, MU Dong. Solving VRPSPDTW Problem Using Simulated Annealing Algorithm[J]. Journal of System Simulation, 2014, 26(11):2618-2623. |
| [9] | 马华伟,靳鹏,杨善林.时变车辆路径问题的启发式算法[J].系统工程学报,2012,27(2):256-262. MA Hua-wei, JIN Peng, YANG Shan-lin. Heuristic Methods for Time-dependent Vehicle Routing Problem[J]. Journal of System Engineering, 2012, 27(2):256-262. |
| [10] | 宁涛,陈荣,郭晨, 等. 一种基于双链量子编码的动态车辆路径问题解决策略[J]. 运筹学学报, 2015,19(2):72-82. NING Tao, CHEN Rong, GUO Chen, et al. A Scheduling Strategy for Dynamic Vehicle Routing Problem Based on Double Chains Coding[J]. Operations Research Transactions, 2015, 19(2):72-82. |
| [11] | 温惠英,孙博. 基于离散粒子群算法的协同车辆路径问题[J]. 公路交通科技, 2011,28(1):149-153,158. WEN Hui-ying, SUN Bo. Resolving Collaborative Vehicle Route Problem Based on Discrete Particle Swarm Optimization[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1):149-153,158. |
| [12] | 李茂军,童调生. 单亲遗传算法及其全局收敛性分析[J]. 自动化学报, 1999, 25(1):71-75. LI Mao-jun, TONG Tiao-sheng. A Partheno Genetic Algorithm and Analysis on Its Global Convergence[J]. Acta Automatica Sinica, 1999, 25(1):71-75. |
| [13] | 肖鹏,李茂军,张军平,等. 车辆路径问题的单亲遗传算法[J]. 计算技术与自动化, 2000,19(1):26-30. XIAO Peng, LI Mao-jun, ZHANG Jun-ping, et al. Partheno Genetic Algorithm for Vehicle Routing Problem[J]. Computing Technology and Automation, 2000, 19(1):26-30. |
| [14] | 李茂军,罗日成,童调生. 单亲遗传算法的遗传算子分析[J]. 系统工程与电子技术, 2001,23(8):84-87. LI Mao-jun, LUO Ri-cheng, TONG Tiao-sheng. Analysis on the Genetic Operators of Partheno-Genetic Algorithm[J]. Systems Engineering and Electronics, 2001, 23(8):84-87. |
| [15] | 李建,张永,达庆利. 第三方物流多车型硬时间窗路线问题研究[J]. 系统工程学报, 2008,23(1):74-80. LI Jian, ZHANG Yong, DA Qing-li. Research on Heterogeneous Vehicle Routing Problem with Hard Time Windows for the Third Party Logistics[J]. Journal of System Engineering, 2008, 23(1):74-80. |
 2016, Vol. 33
2016, Vol. 33
