扩展功能
文章信息
- 彭 伟,李建中
- PENG Wei, LI Jian-zhong
- 黏滞阻尼器用于桥梁减震控制的几个问题及研究现状
- Some Problems and Current Study Situation of Applying Fluid Viscous Dampers in Bridge Seismic Control
- 公路交通科技, 2016, Vol. 33 (6): 76-82
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 76-82
- 10.3969/j.issn.1002-0268.2016.06.012
-
文章历史
- 收稿日期:2015-07-09
2.同济大学 土木工程防灾国家重点实验室, 上海 200092
2. State Key Laboratory for Disaster Prevention in Civil Engineering, Tongji University, Shanghai 200092, China
地震是一种破坏性强的自然灾害。随着桥梁抗震研究的深入, 结构被动控制技术[1, 2, 3, 4]逐渐成为抵抗地震作用、降低结构预期地震响应的热门方法之一, 例如引入减、隔震装置, 提高结构预期抗震性能。
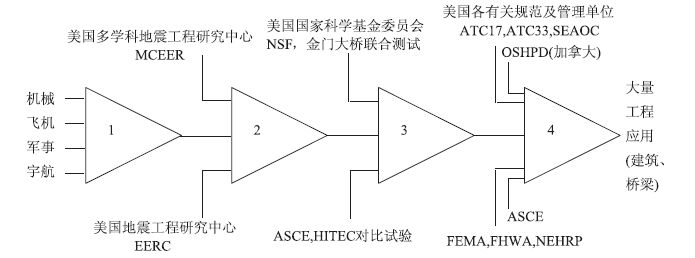
20世纪90年代以来, 广泛用于机械、军工等领域的黏滞阻尼器(Fluid Viscous Damper, 简称FVD)开始用于建筑和桥梁结构的减震控制, 鉴于其具有良好的耗能能力和正常运营条件下不影响结构使用功能等优点, 工程界看好其应用前景, 并积极致力于推广该项技术。其中, 美国科研工作者针对工程结构用黏滞阻尼器的产品研发、试验验证、技术规范编制等方面进行了大量的研究, 总结这些研究工作, 黏滞阻尼器应用于建筑与桥梁结构的发展过程[5]如图 1所示。
|
| 图 1 黏滞阻尼器发展历程 Fig. 1 Development of fluid viscous damper |
首次将黏滞阻尼器应用于桥梁的是美国金门大桥的抗震加固工程, 此后, 国内也有多座桥梁采用黏滞阻尼器改善结构抗震性能, 例如鹅公岩大桥、卢浦大桥、苏通大桥、东海大桥、江阴长江大桥等。从目前收集的资料看, 用于桥梁减震的黏滞阻尼器, 一般安装在结构相对位移较大的部位[6, 7], 例如主梁与桥墩(台)、桥塔之间或相邻主梁之间, 见图 2。

|
| 图 2 黏滞阻尼器安装位置 Fig. 2 Installation positions of FVDs |
与蓬勃的工程应用现状相比, 黏滞阻尼器在国内实际桥梁中的应用时间较短, 普遍缺乏实际地震作用的检验。而且国内对桥梁结构用黏滞阻尼器的研究起步较晚, 目前还没建立实用的黏滞阻尼器参数设计方法, 这既不满足当前工程实践的需要, 也不利于该项技术的推广应用。在此背景下, 本文就桥梁减震用黏滞阻尼器的几个问题进行分析探讨, 以减少桥梁结构使用黏滞阻尼器的盲目性, 并为实际工程用的黏滞阻尼器设计参数选取提供一定的理论支持。
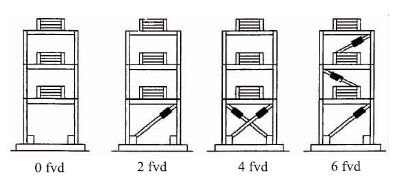
1 线性与非线性黏滞阻尼器减震机理分析认识减震系统或装置的作用机理是减震设计的基础, 世界上最早开展黏滞阻尼器减震机理研究的是美国纽约州立大学Buffalo分校, 部分原因在于其较早开展民用黏滞阻尼器的研制, 能够对黏滞阻尼器的构造、性能等进行系统的研究。例如该校学者Constantinou[2]以附加黏滞阻尼器的钢框架结构模型(图 3)进行了振动台试验, 结果表明在附加黏滞阻尼器后, 第一阶模态阻尼比从1.74%提升为9.9%、17.7%、19.4%, 安装阻尼器个数分别为0,2,4,6, 层间位移相应降低30%~70%, 而且黏滞阻尼器出力与结构位移反相, 黏滞阻尼器在降低结构位移的同时并不会增加结构受力。此后, 世界范围内掀起了关于黏滞阻尼器研制与应用的热潮。
|
| 图 3 黏滞阻尼器减震试验 Fig. 3 Seismic reduction experiment of FVD |
虽然不同机构或厂家的黏滞阻尼器在构造和工作性能上有一定差异, 但从工程应用看, 人们对此类装置的主要疑惑有:这是什么样的装置?能起什么作用?这构成了黏滞阻尼器减震机理的主要内容。
1.1 黏滞阻尼器的力学特性研究对第一个问题的回答涉及到黏滞阻尼器的力学特性研究, 包括黏滞阻尼器的计算模型、黏滞阻尼器出力、滞回特性和耗能能力等方面, 从实现方式上可分为试验研究与数值模拟两大类。
Constantinou[2]在其早期的黏滞阻尼器性能试验中, 研究了不同激励频率、幅值条件下的黏滞阻尼器滞回特性, 确定了所用阻尼器表现纯黏滞行为的截断频率范围(Cut-off Frequency), 并验证了黏滞阻尼器的力学模型、温度稳定性等。尽管该试验所用黏滞阻尼器属于早期产品(小吨位、小行程), 但这无疑具有开创性的意义, 此后, 关于黏滞阻尼器的数值模拟都引用了该试验的某些结论, 其中就包括采用Maxwell模型的合理性。根据Maxwell模型, 黏滞阻尼器出力表达式为:
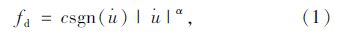
式中, C为黏滞阻尼系数, 这与油缸直径、活塞直径、黏性介质等因素有关, 需试验测定; α为速度指数, 这表征黏滞阻尼器的非线性特征。
翁大根等[8]采用上海材料研究所研制的黏滞阻尼器进行力学性能试验, 结果表明所用黏滞阻尼器具有较好的消能效果, 阻尼力具有较好的调控能力, 但该试验激励频率只在3 Hz以内。
随着黏滞阻尼器逐渐用于实际桥梁工程, 以美国Taylor公司为例[9], 在出厂前都需对黏滞阻尼器进行严格的原型检测, 这些大吨位、大行程条件下的测试结果更有助于了解黏滞阻尼器的性能, 遗憾的是, 这些产品都是针对单个具体工程制造的, 有关这些测试内容和结果的详细、公开技术资料并不多见。在此情况下, 根据试验建立的研究基础, 采用数值仿真是最常用的方法, 这也避免了试验条件的局限, 能分析更多的变量参数及其影响。
在正弦波激励下, 聂利英[10]研究表明黏滞阻尼器滞回曲线不仅和阻尼系数c、速度指数α有关, 而且随激励频率、幅值变化; 周云[11]进一步研究相同速度、不同激励频率和幅值条件下的出力-位移、出力-速度曲线, 结果表明, 尽管激励频率和幅值不同, 但黏滞阻尼器出力峰值相同, 各工况的黏滞阻尼器出力-速度曲线吻合情况很好, 这说明激励幅值和频率变化并不是影响黏滞阻尼器出力的实质因素。这表明活塞运动速度对黏滞阻尼器性能有重要影响, 应该在活塞高、低速运动条件下分别讨论黏滞阻尼器的作用。
为了从理论角度研究黏滞阻尼器, Chopra[12]、Goel[13]建立了黏滞阻尼器在一个循环周期内消耗能量的表达式, 并推导了附加阻尼比ξd计算式, 研究了耗能相同但不同α对出力的影响。这些研究部分揭示了线性(α=1.0)、非线性(α<1.0)黏滞阻尼器在出力与耗能能力等方面的差异, 对于实际应用而言, 还需进一步讨论常用速度指数取值对阻尼器耗能能力的影响, 以及在活塞高、低速运动情况下, 黏滞阻尼器参数取值对附加阻尼比ξd的影响。
1.2 黏滞阻尼器的减震作用分析对第二个问题的回答涉及到黏滞阻尼器对结构动力响应的影响。一个完整的结构动力响应分析, 通常包括计算模型、激励条件、分析方法这3大要素, 但在附加黏滞阻尼器后, 还应考虑阻尼系数 C、速度指数α、附加阻尼比ξd或阻尼器可能的安装位置等。
在理论研究中, 最常用的是单自由度模型, 优点在于能突出黏滞阻尼器的作用, 发现最普遍的规律, 甚至可得解析解(简谐激励条件)。Chopra[12]考虑结构自振周期Tn=0.05~5 s, 附加阻尼比ξd=5%, 15%, 30%, 速度指数α=0.35~1.0, 就正弦波激励下的稳态响应与地震波作用下的瞬态响应进行分析, 结果表明:结构动力响应随ξd增加而降低; 当ξd相同, 在一定的周期范围内, 动力响应基本不受α的影响; 非线性黏滞阻尼器的性能可采用ξd、α这两个相互独立的无量纲数描述, 分别反映黏滞阻尼器的耗能能力、非线性特征。Geol[13]在此基础上进一步研究了考虑结构非线性情况下的减震效果, 以及速度指数对结构动力响应的影响, 但分析限制在Tn≤3 s、ξd=20%。
以上基础性工作对黏滞阻尼器减震研究具有重要的指导意义, 但减震桥梁是长周期(例如飘浮体系斜拉桥)、大阻尼结构, 因此, 有必要扩大结构周期范围、采取更大的附加阻尼比进一步分析。文献[14]研究了在相同c但不同α条件下的结构动力响应, 结果表明在活塞高、低速运动情况下的动力响应规律相反, 但其并没有从阻尼比这个更一般的角度去解释线性、非线性黏滞阻尼器的减震实质。
实际桥梁相对复杂, 并不一定能简化为单自由度体系, 因此常用全桥有限元计算模型, 调整阻尼器参数进行动力分析并总结数据规律, 这样的分析往往是针对具体结构而言, 相关的研究文献较多[15, 16]。与单自由度模型相比, 采用多自由度模型(全桥)的研究更具实践意义, 但结论的适用性非常有限, 难以推广应用。
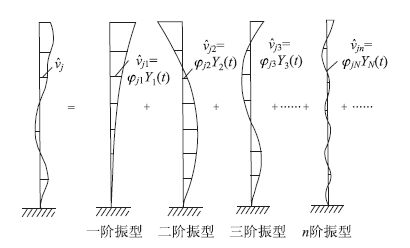
2 附加黏滞阻尼器桥梁的非经典阻尼问题与近似解耦分析结构抗震分析方法, 主要分为模态叠加与直接数值积分两大类。模态叠加法对分析线弹性结构非常有效, 计算效率高, 而且结构地震响应往往由少数低阶振型控制, 采用模态截断技术、只取部分振型进行叠加(图 4)就可得满意的计算效果。基于直接积分的时程方法不受结构弹性假定的限制、适用面广, 能考虑各种非线性因素, 但计算量大、结果处理繁琐, 一般用于特殊结构分析或最终设计阶段的数值验证。
|
| 图 4 模态叠加法示意图 Fig. 4 Schematic diagram of modal superposition method |
模态叠加法是以结构无阻尼振型向量 Φ i建立模态坐标, 要求结构总阻尼矩阵 C 满足关于无阻尼振型矩阵 Φ 的正交性, 由于结构在弹性阶段的阻尼很小, 采用经典阻尼假定后就满足这样的正交性, 例如Rayleigh阻尼[17]。在附加耗能装置后, 结构的整体耗能能力增强, 但各部分的阻尼特性截然不同, 这导致 C 不满足关于 Φ 的正交性, 模态阻尼矩阵含有非零非对角元素Cij*( k≠j), 引起模态耦合, 这就是非经典阻尼问题, 如下所示:(i=1,…,n)
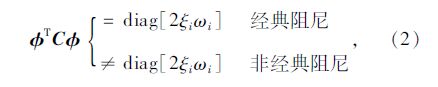
式中, 向量 Φ i已标准化, Φ iT C Φ i= Cii*, ξi、ωi分别为结构第i阶振型的阻尼比与振动频率。
安装黏滞阻尼器的桥梁具有非经典阻尼特性, 由于模态耦合, 不能直接采用模态叠加法分析结构动力响应。围绕这一主题, 从应用角度可将此问题分为两方面:非经典阻尼解耦方法; 非经典阻尼对桥梁结构地震响应的影响及近似解耦范围。
2.1 非经典阻尼解耦方法严格地讲, 实际结构都是非经典阻尼结构, 例如水坝、主次结构、核电站等结构的动力响应都涉及到非经典阻尼问题。国外自20世纪50年代起就对非经典阻尼结构动力响应分析方法进行研究[18], 由此产生大量的研究成果。国内关于非经典阻尼问题的研究较少, 早期的研究[19]侧重于概念定义及数学证明, 随减震(振)技术应用于实际结构, 结构非经典阻尼问题突出。文献[20, 21]对非经典阻尼条件下的一般解进行了研究。
总结这些成果, 非经典阻尼解耦方法可分为复模态解耦与各种近似解耦两大类, 其中, 复模态方法是在2n×2n维空间内完全解耦, 理论上是精确的, 但其物理意义不明确, 计算过程相对复杂, 因此, 该方法主要用于理论研究, 很少用于工程实际, 目前常用的分析软件也很少采用复模态方法。相比较而言, 实模态方法物理意义明确、 计算简便且易于推广。因此, 用传统的实模态方法去求解非经典阻尼结构动力响应的近似方法更受青睐, 即用经典阻尼去近似非经典阻尼, 所以近似解耦就必定存在误差, 在实际应用中就需关注近似解耦误差的大小及其影响因素。
2.2 非经典阻尼对桥梁结构地震响应的影响采用耗能减震技术后, 桥梁非经典阻尼问题突出, 但关于这方面的文献很少, 部分原因如前所述, 即非经典阻尼是在实模态空间内定义的, 用直接积分求解动力方程不会涉及到非经典阻尼问题。
以附加黏弹性阻尼器的连续梁桥为例, Franchin[22]采用复模态与强迫解耦方法计算结构地震响应, 结果表明当结构阻尼比达到30%, 两种方法所得主梁和墩顶纵向位移仍然分别具有良好的吻合情况。清华大学秦权[23]以青马桥、虎门桥为例, 研究结果表明采用2%,5%的经典阻尼模型都会带来较大的误差, 得不出精确解, 并认为大跨悬索桥的抗震抗风动力分析应当使用非经典阻尼模型。林丽霞[24]以双链式悬索桥为例, 研究表明用经典阻尼模型得不出可靠的解, 双链式悬索桥的地震响应分析, 应当使用非经典阻尼模型, 但在初步分析时, 纵、竖向地震下的非经典阻尼体系地震响应可分别按相应的经典阻尼体系进行简化处理。
影响非经典阻尼特性的因素较多, 具体桥型、阻尼器参数及其布置方式都可能引起总阻尼矩阵的变化, 并影响非经典阻尼的程度, 因此, 需要建立更多的分析情况才可得出更具一般性的结论, 并以此明确非经典阻尼对关注桥型动力响应的影响及可近似解耦范围, 这会对抗震分析和设计带来极大的便利。
3 黏滞阻尼器对桥梁结构模态阻尼比的影响桥梁减震属结构被动控制范畴, 即调整结构动力特性以改善动力响应, 由于黏滞阻尼器在截断频率范围内只提供附加阻尼, 因此, 在减震应用中需关注黏滞阻尼器对结构阻尼比的影响, 尤其是主控模态阻尼比的变化情况, 这是实现减震目标的关键。
查阅文献表明, 迄今极少有文献资料提及黏滞阻尼器参数与全桥模态阻尼比的关系, 原因如下:
(1) 结构真实的阻尼特性极其复杂, 影响因素多, 在实际应用中, 通常将各种阻尼耗能现象统一从宏观的角度进行描述, 例如当桥梁处于线弹性阶段, 一般取结构自身阻尼比ξ=2%(钢结构)、ξ=5%(混凝土结构)。
(2) 根据阻尼比定义, 对结构总阻尼矩阵进行特征分析可得模态阻尼比。在安装黏滞阻尼器后, 总阻尼矩阵 C 由自身阻尼矩阵 C s与附加阻尼矩阵 C d构成, C s 可按Rayleigh阻尼理论建立, 但 C d的推导较为困难, 手算或电算都难以给出总阻尼矩阵, 尤其对于多自由度的大跨度桥梁, 这种做法并不现实。
在一般情况下, 结构有限元模型的自由度越多, 计算结果越准确, 但建模的根本原则是把握结构主要的力学特征。因此, 如果建立的计算模型既反映结构力学行为, 又无需太多自由度, 这样的模型就可用于研究结构阻尼比与耗能装置之间的关系, 例如讨论黏滞阻尼器参数对结构主控模态阻尼比的影响, 以此作为黏滞阻尼器设计参数选取的基础。
4 黏滞阻尼器参数设计方法在应用黏滞阻尼器进行结构减震设计时, 最难且最关键的问题在于黏滞阻尼器参数选取, 设计的结果就是黏滞阻尼器厂商生产的依据, 比如黏滞阻尼器出力、阻尼系数、速度指数及活塞行程等。
由于国内对桥梁用黏滞阻尼器的研究相对滞后, 还没有成熟的阻尼器参数设计方法, 《公路桥梁抗震设计细则》(JTG/TB02-01—2008)[25]仅有桥梁减隔震指导原则方面的规定, 缺少完整详细的设计建议。
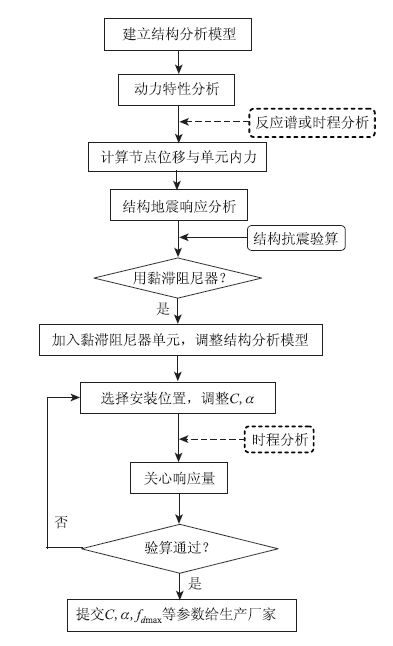
对于单自由度结构, 黏滞阻尼器参数选取相对简单, 但实际桥梁相对复杂, 并非都可简化为单自由度体系。所以实际桥梁用黏滞阻尼器的参数往往是专门设计, 如图 5所示, 采用全桥有限元模型, 调整阻尼器参数及可能的安装位置, 再用非线性时程方法进行计算, 根据参数分析结果总结规律现象, 将最优动力响应对应的一组黏滞阻尼器参数作为最终的‘设计’参数, 这也称为试算法。
|
| 图 5 用时程分析方法设计黏滞阻尼器参数 Fig. 5 FVD parameters designed by time history analysis |
从图 5可见, 试算法计算耗时长、计算量大, 不适合抗震初步设计阶段的计算要求, 而且这种做法只知结果, 不明过程, 缺乏坚实的理论基础, 所‘设计’的参数可能具有一定的盲目性。
一些学者对此开展研究以期解决黏滞阻尼器参数选取问题。J.S Hwang[6]用提高结构总阻尼以考虑附加阻尼的思想, 推导了在给定阻尼比情况下连续梁桥选取黏滞阻尼器的方法, 并用数值证明了其可行性; 叶爱君[26]建议利用径向基函数(RBF)神经网络建立黏滞阻尼器参数与桥梁地震反应之间的映射关系, 以帮助选取所需阻尼器的参数, 但又降低试算的工作量; 李爱群[27]以主跨1490 m的润扬悬索桥为对象, 建立了基于地震位移控制的3种评估函数, 并提出基于罚函数和一阶优化原理的阻尼器最优布置方法。巫生平[28]以淮安大桥为背景, 应用最小二乘回归分析建立关键截面参数与阻尼参数之间的数学模型, 以控制截面内力和变形最小为原则, 通过求解拟合方程的极值推导获得所需最优黏滞阻尼器设计参数。
以上各方法的设计角度不同:最后3种方法是结合地震响应的数学寻优设计, 计算量大、适用性差。J.S Hwang根据黏滞阻尼器的附加阻尼作用, 从减震目标所需阻尼的角度建立简化设计方法, 不仅具有理论基础, 而且也便于在实践中推广。因此, 从工程实用的角度, 在明确具体减震目标后, 建立桥梁总阻尼与附加阻尼的关系, 开展桥梁用黏滞阻尼器设计参数选取方法研究, 是一个可行的方向。
5 结论综上所述, 利用黏滞阻尼器的耗能作用改善新建或既有桥梁的抗震性能正成为应用的热点, 但其减震控制理论研究落后于工程实践的现象也越明显。线性、非线性黏滞阻尼器在出力与耗能能力等方面有明显差异, 但其减震机理都可以从附加阻尼比这个更一般的角度去解释, 同时这种附加阻尼也导致结构非经典阻尼问题并影响结构地震响应, 这需要考虑不同桥梁的动力特性、附加阻尼程度等因素进一步分析。从参数设计的角度, 基于结构总阻尼与黏滞阻尼器附加阻尼的关系, 推导所需的附加阻尼和相应的阻尼器参数, 具有明显的理论基础和实践意义。
| [1] | YAO J T P. Concept of Structural Control[J]. Journal of the Structural Division, 1972, 98(7):1567-1574. |
| [2] | CONSTANTINOU M C, SYMANS M D. Experimental and Analytical Investigation of Seismic Response of Structures with Supplemental Fluid Viscous Dampers, NCEER Rep-92-0032[R]. Buffalo:State University of New York at Buffalo,1992. |
| [3] | SYMANS M D, CONSTANTINOU M C. Passive Fluid Viscous Damping Systems for Seismic Energy Dissipation[J]. ISET Journal of Earthquake Technology,1998,35(4):185-206. |
| [4] | CASAROTTI C. Bridge Isolation and Dissipation Devices:State of the Art Review of Seismic Response and Modelling of Modern Seismic Isolation and Dissipation Devices[D]. Pavia:University of Pavia and ROSE School, 2004. |
| [5] | 陈永祁,耿瑞琦,马良喆.桥梁用液体黏滞阻尼器的减振设计和类型选择[J].土木工程学报,2007, 40(7):55-61. CHEN Yong-qi, GEN Rui-qi, MA Liang-zhe. Design and Selection of Fluid Viscous Devices for Shock Control of Bridges[J]. China Civil Engineering Journal, 2007, 40(7):55-61. |
| [6] | HWANG J S, TSENG Y S. Design Formulations for Supplemental Viscous Dampers to Highway Bridges[J]. |
| [7] | 李正英.大跨度拱桥地震反应特性及减震控制研究[D]. 重庆:重庆大学,2008. LI Zheng-yin. Research on Earthquake Response Characteristic and Seismic Control of Long Span Arch Bridges[D].Chongqing:Chongqing University,2008. |
| [8] | 翁大根, 卢著辉,徐斌,等.粘滞阻尼器力学性能试验研究[J].世界地震工程,2002, 18(4):30-34. WENG Da-geng, LU Zhu-hui, XU Bin, et al. The Experimental Study on Property of Energy Dissipation of Viscous Fluid Damper[J]. World Earthquake Engineering, 2002, 18(4):30-34. |
| [9] | TAYLOR D P, CONSTANTINOU M C. Test Methodology and Procedures for Fluid Viscous Dampers Used in Structures to Dissipate Seismic Energy[R]. North Tonawanda:Taylor Devices, Inc., 1994. |
| [10] | 聂利英,李建中,胡世德,等.任意荷载作用下液体粘滞阻尼器在桥梁工程中减震作用探讨[J].计算力学学报,2007, 24(2):197-202. NIE Li-ying, LI Jian-zhong, HU Shi-de, et al. Investigation of Decreasing Vibration Effects of Fluid Viscous Damper in Bridge Engineering under Random Loads[J]. Chinese Journal of Computational Mechanics, 2007,24(2):197-202. |
| [11] | 周云. 粘滞阻尼减震结构设计[M].武汉:武汉理工大学出版社, 2006. ZHOU Yun. Structure Design of Viscous Damping[M]. Wuhan:Wuhan University of Technology Publishing House,2006. |
| [12] | LIN W H,CHOPRA A K. Earthquake Response of Elastic SDF Systems with Non-linear Fluid Viscous Dampers[J]. |
| [13] | GOEL R K. Seismic Response of Linear and Non-linear Asymmetric Systems with Non-linear Fluid Viscous Dampers[J]. |
| [14] | 蒋建军.桥梁几种典型减隔震装置的减震效果比较与研究[D].上海:同济大学,2005. JIANG Jian-jun. Analysis of Typical Earthquake Mitigation and Isolation Devices for Bridges[D].Shanghai:Tongji University, 2005. |
| [15] | 王志强,胡世德,范立础.东海大桥粘滞阻尼器参数研究[J].中国公路学报,2005, 18(3):37-42. WANG Zhi-qiang, HU Shi-de, FAN Li-chu. Research on Viscous Damper Parameters of Donghai Bridge[J].China Journal of Highway and Transport,2005, 18(3):37-42. |
| [16] | 吴斌暄,王磊, 王歧峰. 使用非线性粘滞阻尼器的桥梁在地震反应中的响应分析[J].公路交通科技,2007,24(10):76-80. WU Bin-xuan, WANG Lei, WANG Qi-feng. A Method of Seismic Response Analysis for Bridge with Nonlinear Viscous Damper[J].Journal of Highway and Transportation Research and Development, 2007,24(10):76-80. |
| [17] | CHOPRA A K. Dynamics of Structures:Theory and Applications to Earthquake Engineering[M]. Englewood Cliffs, New Jersey:Prentice-Hall, 1995. |
| [18] | FOSS K A. Coordinates Which Uncouple the Equations of Damped Linear Dynamic Systems[J]. Journal of Applied Mechanics, 1958, 25:361-364. |
| [19] | 冯振东,吕振华.阻尼系统振动分析的实模态与复模态理论间统一性的探讨[J].吉林工业大学学报,1989, 19(3):64-69. FENG Zhen-dong, LV Zhen-hua. Discussions about the Unity between Real and Complex Modal Formulations of Damped Vibration Theory[J]. Journal of Jilin University of Technology, 1989, 19(3):64-69. |
| [20] | 秦金旗, 唐驾时.非经典阻尼系统的精确解[J].动力学与控制学报,2006, 4(2):136-144. QIN Jin-qi, TANG Jia-shi. Exact Solution of Non-classical Damping Systems[J]. Journal of Dynamics and Control, 2006, 4(2):136-144. |
| [21] | 张淼, 于澜. 对称非经典阻尼系统动力响应精确解算法比较[J]. 长春工业大学学报,2015,36(1):107-110. ZHANG Miao, YU Lan. Algorithm Comparison for the Solution of Symmetric Non-classical Damped System[J]. Journal of Changchun University of Technology, 2015, 36(1):107-110. |
| [22] | FRANCHIN P, MONTI G, PINTO P. On the Accuracy of Simplified Methods for the Analysis of Isolated Bridges[J]. |
| [23] | 秦权,楼磊.非经典阻尼对悬索桥地震反应的影响[J].土木工程学报,1999, 32(3):17-22. QIN Quan, LOU Lei. Effect of Non-proportional Damping on Seismic Response of Suspension Bridges[J]. China Civil Engineering Journal, 1999, 32(3):17-22. |
| [24] | 林丽霞,丁南宏,张元海,等.考虑阻尼值修正的双链式悬索桥地震响应分析[J]. 铁道科学与工程学报,2012, 9(5):25-30. LIN Li-xia, DING Nan-hong, ZHANG Yuan-hai, et al. Seismic Response Analysis of Double Chains Suspension Bridge Considering Modified Damping Value[J].Journal of Railway Science and Engineering, 2012, 9(5):25-30. |
| [25] | JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. JTG/T B02-01-2008, Guidelines for Seismic Design of Highway Bridges[S]. |
| [26] | 叶爱君.径向基函数(RBF)神经网络在桥梁减震设计中的应用仿真[J].系统仿真技术,2006, 2(1):31-37. YE Ai-jun. The Application of RBF Neural Network to Seismic Design of Bridges[J]. System Simulation Technology, 2006, 2(1):31-37. |
| [27] | 李爱群,王浩.大跨悬索桥地震响应控制的阻尼器最优布置方法[J].东南大学学报:自然科学版,2009, 39(2):315-319. LI Ai-qun, WANG Hao. Optimal Placement Method of Dampers for Seismic Control of Long-span Suspension Bridges[J]. Journal of Southeast University:Natural Science Edition, 2009, 39(2):315-319. |
| [28] | 巫生平, 张超, 房贞政. 斜拉桥粘滞阻尼器设计方案及参数回归分析[J] 桥梁建设,2014,44(5):21-26. WU Shen-ping, ZHANG Chao, FANG Zhen-zheng. Design Schemes and Parameter Regression Analysis of Viscous Dampers for Cable-stayed Bridge[J]. Bridge Construction, 2014,44(5):21-26. |
 2016, Vol. 33
2016, Vol. 33
