扩展功能
文章信息
- 徐 岳,展丙来,李 扬,申成岳
- XU Yue, ZHAN Bing-lai, LI Yang, SHEN Cheng-yue
- 钢管混凝土拱桥斜拉扣挂施工扣索索力的优化计算方法
- An Optimum Calculation Method of Cable Force of CFST Arch Bridge in Inclined Cable Hoisting Construction
- 公路交通科技, 2016, Vol. 33 (6): 61-67
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 61-67
- 10.3969/j.issn.1002-0268.2016.06.010
-
文章历史
- 收稿日期:2015-06-10
大跨径钢管混凝土拱桥采用缆索吊装斜拉扣挂法施工时,扣索的初张力直接影响到拱肋的安装线形和成桥受力状态,因此确定合适的扣索初张力是钢管混凝土拱桥缆索吊装斜拉扣挂法施工的关键。
目前,扣索索力的确定方法有零弯矩法、弹性-刚性支撑法、定长扣索法、零位移法以及影响矩阵法等多种方法[1]。其中,零弯矩法索力计算结果有时会出现负值或严重不均衡,需要对扣点位置等因素加以调整,且无法考虑吊装段的切向拼装位移[2];弹性-刚性支撑法在求解索力时需求解高次超静定方程,计算量大且对于弹性支撑的刚度难以准确模拟[3];零位移法实际施工扣索倾角与理论计算值很难相符,因此实际施工中吊点处必定会产生位移;在定长扣索法中,预抬高量的确定十分繁琐,不利于实际应用[4]。刚性支撑连续梁法、内力(应力)平衡法、最小弯曲能量法、用索量最小法等均可用影响矩阵的形式表示,可归结为影响矩阵法。由影响矩阵法求索力时,约束条件的种类选择较广,可取为控制截面的内力、应力、位移、弯曲能量、用索量等,但是要求结构必须满足线性叠加原理,当计入索的垂度效应、切向拼装位移、混凝土收缩徐变等影响时,影响矩阵法将不再适用。
拱桥与梁桥、斜拉桥不同,切向拼装位移对各拼装段的线形影响较大且具有累加效应,在计算过程中必须加以考虑。张建民等[5]通过对拼装构件的节点坐标、转角等进行修正,考虑了切线拼装位移对结构安装线形的影响,通过确定目标函数与约束条件,采用最优化理论确定了斜拉扣挂施工拱桥的合理施工状态;田维锋等[6]分析了大跨径斜拉桥施工控制和结构分析中零杆虚位移的成因及其导致的计算误差,提出了基于无应力状态法理论的误差修正方法,经算例验证是有效可行的;张万晓等[7]针对ANSYS生死单元出现的虚位移,推导了坐标修正公式,引入无应力状态法,使得分阶段施工的拱桥内力、线形与一次落架的裸拱计算结果一致;戴鹏等[8]采用随动坐标迭代法,基于优化理论及前进分析法,考虑几何非线性效应对缆索吊装过程的影响,更精确地模拟了缆索吊装的施工过程,且分析结果正确有效。但是,以上各分析方法求解过程均较繁琐,不便于工程应用。
本文基于扣索索力对各扣点位移的影响矩阵,以成拱阶段各扣点的位移值为约束条件,引入优化分析理论,确定扣索张力迭代初值,然后采用正装插值迭代法求解适于斜拉扣挂施工钢管混凝土拱桥的一次张拉扣索索力,使得计入切向拼装位移影响的安装线形能够达到目标要求。
1 基本理论与实现方法 1.1 影响矩阵法斜拉扣挂施工的拱桥扣索力的计算类似于斜拉桥的施工索力计算,只是前者不存在成桥索力,但拱桥扣索索力的计算也应考虑到拱肋合龙以至桥面铺装完成后的成桥线形,因此可以参考斜拉桥施工的索力计算[9]。
影响矩阵法目前多用于斜拉桥合理成桥状态的索力优化及施工阶段索力的确定,影响矩阵法的计算过程中,如果结构满足线性叠加原理,且记受调向量为 D 、施调向量为 x 、影响矩阵为 A ,则受调向量为 D 与影响矩阵为 A 须满足下列方程[10]:

影响矩阵表达的只是一种索力与位移之间的矩阵关系,并不能直接求出索力值,可以通过选定合适的目标函数与约束条件,对式(1)采用线性规划法进行索力求解。
1.2 最优解理论(1)黄金分割法
对于单参数变量问题,当无法由某种确定的函数关系确定最优解,而又能根据经验确定最优解的一维变量区间[a,b]时,可以采用黄金分割法。黄金分割法又称0.618法,依照去坏留好原则、对称原则及等比收缩原则[11],算法简单,效果显著。
(2)线性规划
当需要求得多个控制变量在满足一定约束条件下的最优解时,通过给定控制变量与被约束值间的线性函数关系,确定目标函数,即可应用线性规划的理论确定最优解。由于影响矩阵给出的位移与索力之间是满足线性叠加关系的,所以可以引入线性规划理论来进行索力的优化。建立线性规划数学模型的主要步骤包括:
① 建立约束条件及目标函数;
② 得到约束条件所表示的可行域;
③ 在可行域内求目标函数的最优解。
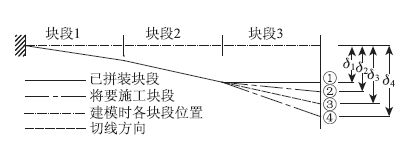
1.3 切向拼装位移影响[12]钢结构或预制混凝土结构采用悬臂拼装施工时,需要考虑悬臂端部各个施工阶段发生的切向角位移,否则无法实现各块段之间的无缝拼接。以图 1所示的悬臂拼装结构为例,拼装块段3时,①号线为块段单元的激活方向;②号线为若不计入切向拼装影响,块段3拼装后在施工荷载及自重作用下的位置。因此(δ2-δ1)为不计切向拼装影响,块段3端点当前施工阶段的位移,δ2为不计切向拼装位移影响块段3端点施工至此步时的累计位移;③号线为块段2、3接点位置处沿块段2的切线方向;④号线为若计入切向拼装影响,块段2在施工荷载及自重作用下的位置。因此(δ4-δ1)为计入切向拼装影响,块段3端点当前施工阶段的位移,δ4为计入切向拼装影响块段3端点施工至此步时的实际位移[6]。
由图 1可见,切向拼装位移的计入与否,会给各拼装扣点的当前步骤位移带来差异,这一差异会随着施工进程而增大,在最后一个施工阶段达到最大,导致合龙线形受到显著影响。对于斜拉扣挂施工拱桥来说,为了保证有限元计算结果与实际工程要求相符,必须计入切向拼装位移的影响,而这将导致结构不再满足线性叠加原理。所以,对于计入切向拼装位移影响施工的斜拉扣挂施工拱桥,由影响矩阵法求得的索力与实际一次张拉索力存在误差,需要进一步调整。
|
| 图 1 当前安装阶段切向位移影响 Fig. 1 Effect of tangential displacement on current mounting phase |
根据以上分析,针对大跨度拱桥不对称斜拉扣挂施工的特点,同时为了实现安装拱肋扣索一次张拉施工的目的,扣索索力可按以下步骤确定:
(1)确定影响矩阵
对于斜拉扣挂施工的拱桥,可取计入预拱度的拱肋坐标线形为目标安装线形,即若以计入预拱度的坐标建立有限元模型,则拱肋合龙并拆除扣索后,若各关键节点处于建模时的坐标处,即认为满足合龙目标线形要求。
因此,以拱肋合龙并拆除扣索后的拱肋关键节点(扣点)位移值为约束条件,当位移值为0时,则必定满足合龙目标的线形要求。为了达到一次张拉施工的目的,使拱肋合龙后的线形刚好落在设计标高位置,取位移值的一个较小范围[p,q]作为约束条件,既保证拱肋变形不至太大,又为以后的线性规划提供充足的可行域。建立有限元模型,确定计入施工阶段扣索索力对于扣点位移的影响矩阵:

式中,A 为影响矩阵,即索力的变化对扣点位移值的影响矩阵; x 为施调向量,即由各索力值组成的向量; D 为受调向量,即由各扣点在拱肋合龙阶段的位移值组成的向量。
(2)引入线性规划理论
设左岸扣索i索力值为ai,扣点i位移值为mi,右岸扣索j索力值bj,扣点j位移值为nj。以各索力值的方差为目标函数F:
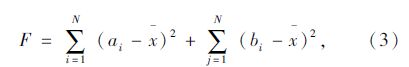
式中,$\bar{x}=\frac{\sum\limits_{i=1}^{6}{{{a}_{i}}}+\sum\limits_{j=1}^{6}{{{a}_{j}}}}{2N}$,为索力平均值;N为一岸侧扣索数量。
确定约束条件:
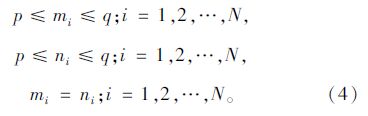
联立影响矩阵中索力与位移值的关系,求解目标函数最小时的索力值。
(3)应用黄金分割法正装迭代
由于切向拼装位移影响的计入,需对由影响矩阵法求得的索力进行调整。将索力作为迭代初值导入有限元模型运算,得到该组索力下各扣点的实际位移值,根据位移值对单根索力或多根索力进行调整。
首先可从最大实际位移值处开始调整索力,由于扣点处位移受当前段扣索索力的影响最大,所以对于每一个扣点位移值,视其受对应的扣索索力单参数影响。根据经验选取合理的单步步长S,当扣点位移δ<时,将索力增加S再次迭代;当扣点位移δ>q时,将索力减小S再次迭代。直至迭代至某步时位移值的变化跨越区间[p,q],则在上一步至该步的步长S区间内采用黄金分割法不断搜索合适索力直至位移值满足约束条件。
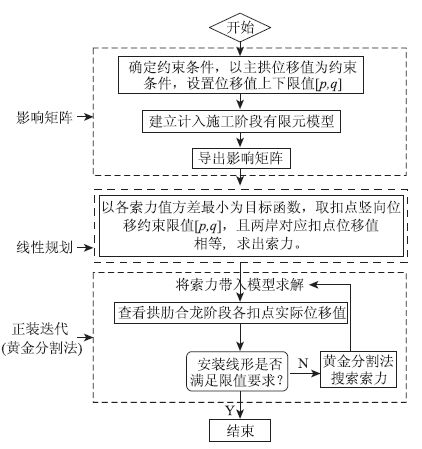
搜索索力时只针对当前阶段,确定当前索力合理步长,对于每一岸的N个扣索,依次筛选合适索力,这样每搜索N次为一轮。事实上,N根扣索力与N个扣点位移值是相互影响的,如当索i值合适时虽然扣点i的位移值满足限值要求,可能会导致本来已经满足位移约束条件的扣点j位移值再次超限。因此,只有当拱肋合龙阶段所有扣点的位移值均在给定的约束范围[p,q]中时,认为该组索力达到收敛目标,可停止迭代。扣索索力确定流程如图 2所示。
|
| 图 2 扣索索力确定流程 Fig. 2 Procedure for determine stayed-buckle cable force |
实桥采用中承式有推力钢管混凝土拱桥结构,计算跨径248 m,计算矢高比1/4,拱轴线为m=1.5 的悬链线,桥道系全宽16 m,设计速度80 km/h,上下行双向六车道,车辆荷载取公路-I级。
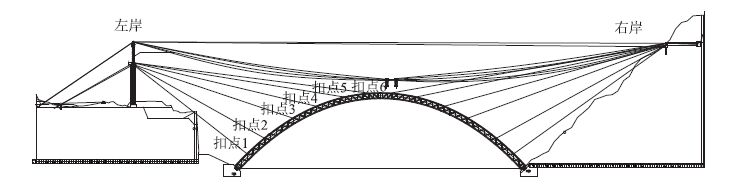
主拱施工采用无支架缆索吊装施工方法,全拱共12个吊装段和一个合龙段,受地形条件的限值,左岸采用主塔、扣塔合一,主塔扣塔铰接的形式,而右岸将扣索直接锚固于锚碇,这也造成了两岸吊装扣索倾角和距离的不对称性,如图 3所示。
|
| 图 3 实桥不对称斜拉扣挂施工示意 Fig. 3 Schematic diagram of asymmetric cable hoisting construction of real bridge |
(1)确定影响矩阵
取拱肋合龙后各扣点的位移上限为0,位移下限为-3 mm。
建立计入施工阶段的有限元模型,分别确定左岸与右岸各索索力值的变化对于各扣点位移的影响矩阵,见表 1及表 2。需要指出,利用影响矩阵求得的位移值均未计入切向拼装位移影响。
| 索力值/kN | 位移值/mm | |||||
| 1#扣点 | 2#扣点 | 3#扣点 | 4#扣点 | 5#扣点 | 6#扣点 | |
| 1#索 | 0.777 04 | 0 | 0 | 0 | 0 | 0 |
| 2#索 | 0.297 93 | 0.811 68 | 0 | 0 | 0 | 0 |
| 3#索 | 0.094 66 | 0.261 50 | 0.486 32 | 0 | 0 | 0 |
| 4#索 | 0.051 67 | 0.145 25 | 0.280 96 | 0.425 58 | 0 | 0 |
| 5#索 | 0.032 38 | 0.093 11 | 0.188 88 | 0.302 68 | 0.456 47 | 0 |
| 6#索 | 0.019 40 | 0.056 73 | 0.118 98 | 0.197 57 | 0.311 00 | 0.446 27 |
| 索力值/kN | 位移值/mm | |||||
| 1#扣点 | 2#扣点 | 3#扣点 | 4#扣点 | 5#扣点 | 6#扣点 | |
| 1#索 | 1.002 89 | 0 | 0 | 0 | 0 | 0 |
| 2#索 | 0.383 87 | 1.044 31 | 0 | 0 | 0 | 0 |
| 3#索 | 0.118 93 | 0.327 05 | 0.604 65 | 0 | 0 | 0 |
| 4#索 | 0.064 46 | 0.179 81 | 0.343 44 | 0.514 59 | 0 | 0 |
| 5#索 | 0.040 39 | 0.114 86 | 0.228 66 | 0.360 22 | 0.535 78 | 0 |
| 6#索 | 0.025 42 | 0.073 43 | 0.150 91 | 0.246 18 | 0.382 20 | 0.544 03 |
由表 1和表 2可以看出,由于两岸分别进行施工互不影响,扣索采用一次张拉施工,当前阶段的索力不会对以后阶段扣点的位移值造成影响,所以计入施工阶段的影响矩阵一定是两个三角矩阵。
(2)引入线性规划
由式(3),得目标函数$F={{\sum\limits_{i=1}^{6}{\left( {{a}_{i}}-\bar{x} \right)}}^{2}}+{{\sum\limits_{j=1}^{6}{\left( {{b}_{i}}-\bar{x} \right)}}^{2}},$式中$\bar{x}=\frac{\sum\limits_{i=1}^{6}{{{a}_{i}}}+\sum\limits_{j=1}^{6}{{{b}_{j}}}}{12}$。
由式(4),得约束条件:
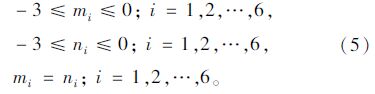
联立影响矩阵中索力与位移值的关系,限于篇幅,此处仅以左岸3#扣点位移m3为例: m3=0.486 32×a3+0.280 96×a4+0.188 88×a5+0.118 98×a6-652.785 35。
类似地,可得左岸扣点位移m1~m6关于索力a1~a6的表达式,及汉中岸扣点位移n1~n6关于索力b1~b6的表达式。求目标函数F在满足式(5)所列约束条件下达到最小时的索力值见表 3。
| 位置 | 索号 | |||||
| 1# | 2# | 3# | 4# | 5# | 6# | |
| 左岸 | 118 | 323 | 467 | 470 | 737 | 1 298 |
| 右岸 | 118 | 329 | 474 | 476 | 705 | 1 169 |
由表 3可见,由于扣索构形的不对称性,为了达到两岸对应扣点位移值相等,必然会使两岸索力产生差别,但是索力变化规律是相同的,索力值从1#至6#均逐渐增大。
将表 3中的各索力值作为扣索张力迭代初值,带入有限元计算模型,考虑切向拼装位移影响,求得各扣点位移值,见表 4。
| 位置 | 扣点号 | |||||
| 1# | 2# | 3# | 4# | 5# | 6# | |
| 左岸 | -2.20 | -3.00 | -0.64 | 5.42 | 23.80 | 59.75 |
| 右岸 | -3.54 | -4.89 | -1.04 | 6.30 | 23.86 | 56.88 |
由表 4可知,当计入切向拼装位移影响时,大多扣点位移超出约束限值[-3,0] mm且不满足对称施工的要求。由第1.3节的分析可知,对于斜拉扣挂施工的拱桥,为了保证各个块段间的拼接符合工程要求,必须计入切向拼装位移影响。因此,基于影响矩阵求出的扣索张力迭代初值需进一步调整。
(3)正装迭代
由表 4可见,实际位移最大值位于左岸第6段扣点处,为59.75 mm。因此可从左岸6号扣索开始调整,根据经验可选取50 kN为步长,降低索力以减小位移值,直至迭代至某步时位移值小于-3 mm,则在上一步至该步的50 kN区间内采用0.618法插值搜索合适索力,直至位移值落入[-3,0] mm区间,然后可采用同样方法对下一根索力值进行调整。
当所有扣点的位移值均在约束范围[-3,0] mm内时,认为该组索力收敛,可停止迭代。
将扣索张力迭代初值与满足收敛目标的扣索张力迭代终值对比分别见表 5及表 6,扣索张力迭代终值下各扣点位移计算结果见表 7。
| 扣索号 | 扣索张力迭代初值/kN | 扣索张力迭代终值/kN | 相对误差/% |
| ① | ② | (②-①)/①×100 | |
| 1#索 | 118 | 119 | 0.85 |
| 2#索 | 323 | 325 | 0.62 |
| 3#索 | 467 | 475 | 1.71 |
| 4#索 | 470 | 495 | 5.32 |
| 5#索 | 737 | 761 | 3.26 |
| 6#索 | 1 298 | 1 175 | -9.48 |
| 扣索号 | 扣索张力迭代初值/kN | 扣索张力迭代终值/kN | 相对误差/% |
| ① | ② | (②-①)/①×100 | |
| 1#索 | 118 | 119 | 0.85 |
| 2#索 | 329 | 331 | 0.61 |
| 3#索 | 474 | 475 | 0.21 |
| 4#索 | 476 | 500 | 5.04 |
| 5#索 | 705 | 729 | 3.4 |
| 6#索 | 1 169 | 1 061 | -9.24 |
| 左岸 | 1#扣点 | 2#扣点 | 3#扣点 | 4#扣点 | 5#扣点 | 6#扣点 |
| 位移 | -0.40 | -0.22 | 0.00 | -1.16 | -2.93 | -1.22 |
| 右岸 | 1#扣点 | 2#扣点 | 3#扣点 | 4#扣点 | 5#扣点 | 6#扣点 |
| 位移 | -1.82 | -2.42 | -2.69 | -1.52 | -1.85 | -2.61 |
由表 5、表 6可知,迭代前后索力值最大相对误差小于10%,说明切向拼装位移对一次张拉索力值的影响并不大。可见,基于影响矩阵由线性规划求出的索力值准确度较高,作为迭代初值可大大加快收敛速度。且在迭代过程刚开始确定每根扣索力调整的合理步长时,一般取值不应超过迭代初值的10%,即可很快找到搜索区间,应用黄金分割法搜索最合适索力。
由表 7可见,当计入切向拼装位移影响时,以基于影响矩阵求得的索力为迭代初值,采用黄金分割法搜索迭代出最优索力,此时所有扣点在拱肋合龙阶段的位移值均满足最初设定的[-3,0] mm的约束条件,证明所给方法正确有效,且能够实现一次张拉施工达到拱肋安装线形要求。
(4)理论值与监控数据对比
取施工监测得到的数据与上文得到的理论计算值进行对比,由于现场场地实际条件限制,只取右岸前3个扣索值比对,结果见表 8。
| 扣索号 | 理论值 | 施工监控值 | 相对误差 |
| ① | ② | (②-①)/①×100% | |
| 1#索 | 119 | 118.6 | -0.34 |
| 2#索 | 331 | 324.3 | -2.02 |
| 3#索 | 475 | 474.9 | -0.02 |
由表 8可以看出,计算所得索力理论值与实际施工监测值相对误差均在5%以内,证明本文所提出的扣索力计算方法可行可靠。
3 结论本文通过影响矩阵法确定扣索张力迭代初值,计入切向拼装位移的影响,采用黄金分割法并通过正装插值迭代搜索适合一次张拉的优化索力,提出了钢管混凝土拱桥斜拉扣挂施工扣索索力的确定方法,通过实桥应用及分析,可得出以下主要结论:
(1)基于影响矩阵,以拱肋变形为约束条件,以索力方差最小为目标,用线性规划求解扣索索力的方法,适用于不计切向拼装位移影响的一次张拉施工,求得的索力值与计入切向拼装影响的一次张拉索力相对误差小于10%,索力值可为施工单位准备施工机具提供参考。
(2)对于斜拉扣挂施工的钢管拱肋结构,切向拼装位移对安装线形影响较大,而对索力的影响较小,说明在一次张拉施工过程中,扣索初张力较小的变化对于拱肋安装线形即能引起较大的改变。因此,对于以位移为控制目标诸如斜拉扣挂施工的拱桥,必须计入切向拼装位移的影响。
(3)提出了扣索索力的优化计算方法,包括:建立有限元模型,确定扣索索力对扣点位移的影响矩阵;给定约束条件与目标函数,利用线性规划求解扣索张力迭代初值;计入切向拼装位移影响,采用黄金分割并正装迭代计算直至满足收敛目标对索力进行调整,求得一次张拉索力值。实桥应用表明,优化计算方法步骤清晰,方便有效,可以实现扣索一次张拉达到拱肋安装线形的期望要求。
| [1] | 梅盖伟,张勇,高雄.拱桥缆索吊装法施工中索力计算方法的探讨[J].重庆建筑,2012,108(11):42-44. MEI Gai-wei,ZHANG Yong,GAO Xiong. Calculation Method of Cable Force of Arch Bridge in Cable-hoisting Construction[J].Chongqing Architecture,2012,108(11):42-44. |
| [2] | 张玉平,李传习,董创文."零弯矩法"应用于斜拉扣挂索力确定的讨论[J].长沙交通学院学报,2004,20(1):15-18. ZHANG Yu-ping, LI Chuan-xi, DONG Chuang-wen. Discussion on "Zero Moment Method" in the Cable Calculation of Cable-stay[J].Journal of Changsha Communications University,2004,20(1):15-18. |
| [3] | 刘智慧,喻光勇,乔文庭.大跨度钢管混凝土拱桥拱肋吊装施工索力计算方法探讨[J].北方交通,2013,246(10):29-32. LIU Zhi-hui,YU Guang-yong,QIAO Wen-ting. The Calculating Method Discussion on the Lifting Construction Cable Force of Longspan Concrete-filled Steel Tubes Arch Bridge and Arch Rib[J].Northern Communications,2013,246(10):29-32. |
| [4] | 刘书杰.外倾式钢箱拱桥扣索吊装拱肋线形控制[D].上海:同济大学,2008. LIU Shu-jie. Line Shape Control of Steel Box Arch Rib of External Slanted Arch Bridge[D].Shanghai:Tongji University,2008. |
| [5] | 张建民, 郑皆连, 肖汝诚. 钢管混凝土拱桥吊装过程的最优化计算分析[J]. 中国公路学报, 2005, 18(2):40-44. ZHANG Jian-min, ZHENG Jie-lian, XIAO Ru-cheng. Calculation Method for Optimizing the Installation Process of Concrete-filled Steel Tube Arch Bridge[J]. China Journal of Highway and Transport,2005,18(2):40-44. |
| [6] | 田维锋, 周水兴, 秦镇. 基于无应力状态法的零杆虚位移修正[J]. 重庆交通大学学报:自然科学版, 2010, 29(1):20-22. TIAN Wei-feng, ZHOU Shui-xing, QIN Zhen. Modification of Virtual Displacement Based on Unstressed State Method[J].Journal of Chongqing Jiaotong University:Natural Science Edition, 2010, 29(1):20-22. |
| [7] | 张万晓, 杨昌龙, 周水兴, 等. 基于无应力状态法的拱桥悬臂施工控制方法研究[C]//中国土木工程学会桥梁及结构工程分会.第二十一届全国桥梁学术会议论文集(上册).北京:人民交通出版社,2014:785-789. ZHANG Wan-xiao, YANG Chang-long, ZHOU Shui-xing, et al. Study on Control Methods for Arch Bridge Cantilever Construction Based on Unstressed State Method[C]//Bridge and Structures Engineering Branch of China Civil Engineering Institute. Proceedings of 21st National Bridge Academic Conference(Volume I). Beijing:China Communications Press,2014:785-789. |
| [8] | 戴鹏, 谢功元, 郝宪武,等. 大跨径钢管混凝土拱桥缆索吊装非线性分析[J]. 武汉理工大学学报, 2007, 29(2):114-117. DAI Peng, XIE Gong-yuan, HAO Xian-wu, et al. Nonlinear Analysis of Cable-hoisting Construction of Long-span Concrete Filled Steel Tube Arch Bridge[J].Journal of Wuhan University of Technology,2007,29(2):114-117. |
| [9] | 周叶军.悬臂浇筑钢筋混凝土拱桥最优扣索索力计算方法研究[D].成都:西南交通大学,2008. ZHOU Ye-jun. Study on Calculation Method of Optimal Stayed-buckle Cable Force for Reinforced Concrete Arch Bridge with Cantilever Cast Method[D].Chengdu:Southwest Jiaotong University,2008. |
| [10] | 方鸿,高琼.影响矩阵法在系杆拱桥施工调索中的应用[J].中外公路,2014,34(6):146-148. FANG Hong,GAO Qiong. Application of Influence Matrix Method in Cable Adjustment of Tied Arch Bridge[J].Journal of China & Foreign Highway,2014,34(6):146-148. |
| [11] | 宋永东,张玉强,张建华.黄金分割法用于PID参数优化整定技术的研究[J].西安工程科技学院学报,2007,21(2):262-266. SONG Yong-dong,ZHANG Yu-qiang,ZHANG Jian-hua. Optimized PID Parameter Adjustment Technology Based on Golden Section Law[J]. Journal of Xi'an University of Engineering Science and Technology,2007,21(2):262-266. |
| [12] | 肖伟.超大跨度钢管混凝土拱桥施工过程中扣索索力计算方法研究[D]. 重庆:重庆交通大学, 2011. XIAO Wei. Research on Cable Force Calculation Methods for Construction of Super Long-span CFST Bridge[D]. Chongqing:Chongqing Jiaotong University,2011. |
 2016, Vol. 33
2016, Vol. 33
