扩展功能
文章信息
- 李 盛,王起才,马 莉,于本田,郭玉柱
- LI Sheng, WANG Qi-cai, MA Li, YU Ben-tian, GUO Yu-zhu
- 不同含气量水泥砂浆孔体积分形维数研究
- Study on Pore Volume Fractal Dimension for Cement Mortar with Different Air Contents
- 公路交通科技, 2016, Vol. 33 (6): 54-60
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 54-60
- 10.3969/j.issn.1002-0268.2016.06.009
-
文章历史
- 收稿日期:2015-07-24
2.兰州工业学院 土木工程学院,甘肃 兰州 730050
2. School of Civil Engineering, Lanzhou Institute of Technology, Lanzhou Gansu 730050, China
混凝土中的水泥经过水化反应生成了固体水化产物和孔结构[1],孔结构特征强烈地影响着混凝土材料的抗渗性、气密性、抗冻性、抗腐蚀性等物理特性和强度、刚度、韧性等力学行为,是混凝土材料科学中细观层次研究的重要课题,在国际上许多混凝土专家甚至把孔作为混凝土中的一个重要的组分[2, 3, 4],因此,对孔结构特征研究显得尤为重要。分形理论作为描述物质复杂性、不规则性的新兴学科,众多学者将其引入并逐渐应用到描述混凝土的微孔结构中,将孔结构的复杂程度量化为分形维数。李永鑫[5]、喻乐华[6]、宋军伟[7]、金珊珊[8]、Arandigoyen[9, 10]分别研究了水泥浆中掺加粉煤灰、珍珠岩、磷渣、石灰后其龄期、强度及孔结构参数与分形维数的关系;唐明[11]分析了不同水化龄期下冻融前后普通水泥和硫铝酸盐水泥分形维数的变化;王剑[12]探讨了不同矿物掺合料高流动混凝土分形维数与孔结构分布特征及抗冻性的关系;尹红宇[13]构造了孔轴线分形模型,研究了孔轴线分形维数与孔轴曲率、渗透系数的关系,以上的研究均取得了一些积极有价值的研究成果,为分形维数在混凝土科学及工程领域的应用奠定了基础。
依此,本文首先通过压汞试验得到了不同含气量水泥砂浆孔结构参数,再利用热力学关系分形模型,确定了不同含气量水泥浆体的不同尺度孔结构分形维数,进而对分形维数与孔结构参数的关系进行了探讨。
1 基于热力学关系的分形模型基于热力学关系的分形模型最早由张宝泉等[14]提出,后经陈三强[15, 16]等在其基础上改进,该模型计算方法如下:
采用压汞法测量多孔物料孔隙体积与孔径的关系时,外界环境对汞所作的功等于进入孔隙内汞液的表面能增加量,所施加于汞的压强P和进汞量V满足:
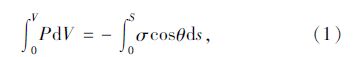
式中,σ为汞表面张力;θ为汞液与固体孔壁的接触角。
通过量纲分析,可将多孔物料孔隙表面积S的分形标度与孔径r、进汞量V进行关联,得到孔隙分形维数Ds的表达式。对于进汞操作,可将式(1)近似写成离散形式[15, 16]:
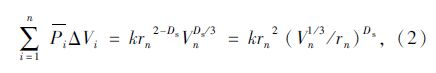
式中,Pi为第i次进汞操作的平均压力;ΔVi为第i次进汞操作的进汞量;n为在进汞操作中施加的间隔数;rn为第n次进汞所对应的孔隙半径;Vn为压力间隔1~n时的累积进汞量;Ds为基于热力学关系的分形维数;k为系数。
令
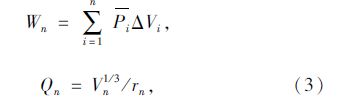
将式(3)代入式(2),并对两边取对数,得:
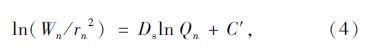
式中C′为常数。
由式(4)可知,该方程关联了压汞过程的施加压力P和进汞量V,故令n=1,2,3,…,直接采用压汞仪测定数据求出一系列Wn/rn2和Qn,然后,对二者取对数,以lnQn为横坐标,ln (Wn/rn2)为纵坐标,绘制散点图,并添加趋势线进行线性回归,得到回归方程及相关系数R2。如果相关系数较高,则表明孔结构特征具有明显的分形特征,所得到的直线斜率即为该多孔物料的分形维数Ds;如果相关系数较低,则表明孔结构不符合分形模型,且分形维数不能由此确定。
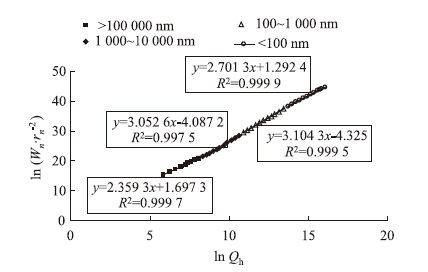
取养护龄期28 d的JZ试样为例进行说明,其不同尺度孔径范围的分形维数计算结果如图 1所示。由图中可以看出,不同尺度孔结构都具有明显的分形维数,相关系数均大于0.99,表明水泥砂浆不同尺度孔结构可以采用热力学分形模型,且随着孔径范围从100 000~10 000 nm变化到小于102 nm,分形维数先从2.359增大到3.104,后减小到2.701,呈先增大后减小的趋势。采用类似方法可以计算出其他水泥砂浆试样不同龄期的分形维数及其相关系数。
|
| 图 1 JZ水泥砂浆试样不同尺度孔结构分形维数 Fig. 1 Different scales' pore structure fractal dimensions of JZ cement mortar |
水泥采用甘肃某水泥有限公司生产的42.5级普通硅酸盐水泥,各项性能满足标准要求;砂子采用庄浪河砂,中砂,细度模数为2.68,含泥量1.6%,表观密度2.66 g/cm3,堆积密度1 559 kg/m3;矿物掺合料是由硅灰、粉煤灰、矿渣按比例配合而成;粉煤灰采用兰州热电厂的Ⅰ级粉煤灰,矿渣粉为安徽某水泥有限公司生产的Ⅲ级矿渣粉,硅灰为西北铁合金厂生产,性能满足要求,检测依据为《高强高性能混凝土用矿物外加剂》(GB/T18736—2002);所掺化学外加剂为PCA-Ⅰ 聚羧酸高性能减水剂和SJ-2型液体引气剂。试验用4种水泥砂浆胶凝材料,总量均为600 kg/m3,其中水泥掺量为422 kg/m3,粉煤灰掺量为100 kg/m3,矿粉掺量为60 kg/m3,硅灰掺量为18 kg/m3,单位用水量为240 kg/m3,砂浆水胶比均为0.40,砂子用量为1 520 kg/m3,高性能减水剂掺量为胶凝材料的1.0%。JZ为基准混凝土不掺引气剂,LSY1为混凝土引气剂掺量0.005%,LSY2为混凝土引气剂掺量0.01%,LSY2为混凝土引气剂掺量0.015%。
2.2 试验方法本试验主要是对各不同含气量下水泥砂浆孔结构进行分析,得到孔结构各参数值大小。试验采用压汞法,养护龄期分别为3,7,28 d,试件按汞压力测孔对试样的要求和处理进行制作[17],仪器使用美国某公司生产的 AutoPore IV9500全自动压汞仪。孔间距系数测定采用RapidAir457型硬化混凝土气孔结构分析仪,测试试件由100 mm×100 mm×400 mm切割成100 mm×100 mm×100 mm 的试件,将其表面进行研磨平后涂刷荧光剂并风干,养护龄期为28 d。
3 结果分析 3.1 不同含气量水泥砂浆孔结构试验结果不同含气量和龄期的水泥浆体孔结构试验结果见表 1、图 2~图 5所示。
| 样本编号 | 含气量 (新拌)/% | 龄期/d | 总孔体积/(ml·g-1) | 总孔面积/ (m·kg-1) | 比表面积/mm | 平均孔径/nm | 孔隙率/% |
| JZ | 2.3 | 3 | 0.081 5 | 3.21 | 39.33 | 87.5 | 20.03 |
| 7 | 0.075 6 | 3.52 | 46.59 | 65.4 | 18.75 | ||
| 28 | 0.068 7 | 4.07 | 59.24 | 40 | 14.37 | ||
| LSY1 | 3 | 3 | 0.089 8 | 3.66 | 40.72 | 99.1 | 22.47 |
| 7 | 0.081 4 | 3.85 | 47.26 | 77.3 | 20.34 | ||
| 28 | 0.069 4 | 4.63 | 66.73 | 49.3 | 16.63 | ||
| LSY2 | 4.9 | 3 | 0.090 2 | 3.64 | 40.32 | 98.2 | 23.14 |
| 7 | 0.086 1 | 4.46 | 51.74 | 84.6 | 21.54 | ||
| 28 | 0.076 3 | 5.53 | 72.41 | 64.8 | 17.21 | ||
| LSY3 | 6.2 | 3 | 0.110 2 | 3.86 | 35 | 123.9 | 27.04 |
| 7 | 0.093 | 4.74 | 51 | 107.2 | 23.05 | ||
| 28 | 0.087 5 | 5.85 | 66.86 | 70.3 | 21.13 |
|
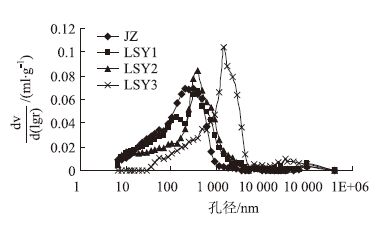
| 图 2 水泥砂浆孔径分布微分曲线 Fig. 2 Pore diameter distribution differential curve of cement mortar |

|
| 图 3 不同含气量水泥砂浆不同尺寸孔径分布图 Fig. 3 Pore diameter distribution of cement mortar with different air contents |
|
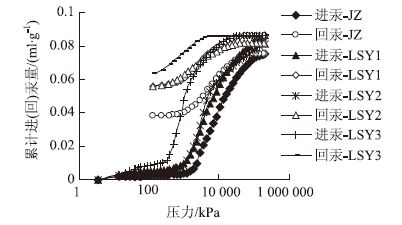
| 图 4 不同含气量水泥砂浆累积进汞量和回汞量与压力关系 Fig. 4 Relationships between cumulative inlet and return mercury contents and pressure of cement mortar with different air contents |
|
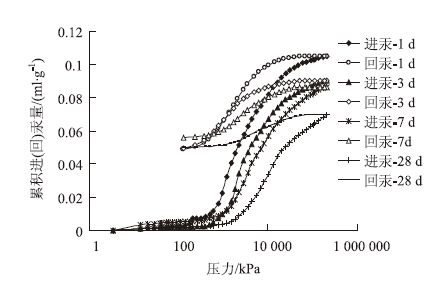
| 图 5 不同龄期水泥砂浆累积进汞量和回汞量与压力关系 Fig. 5 Relationships between cumulative inlet and return mercury contents and pressure on different aged cement mortar |
从表 1、图 2~图 5可以看出:
(1)龄期相同时,与JZ水泥浆体孔结构相比,含气量大的水泥浆体其孔隙率、总孔体积、平均孔径均增大,孔间距系数减小,累积进汞量明显增加,减小了小于100 nm孔所占总孔比例,明显增加了100~1 000 nm孔所占比例,28 d的LSY3水泥砂浆孔径分布相对均匀,说明掺入引气剂增大了孔隙率、平均孔径,减小了孔间距系数;
(2)当水泥砂浆配合比一定时,随着龄期的增大,其孔隙率、总孔体积、平均孔径减小,孔总面积、比表面积增大,累积进汞量明显减小,累积回汞量基本一致,大于1 000 nm的孔所占总孔比例减小,100~1 000 nm及小于100 nm孔明显增加。这是因为水泥砂浆的凝结和硬化过程中,水泥和水之间发生物理和化学变化,水化初期水泥砂浆中大的毛细孔比较多,孔隙的总体积大,随着龄期的增加,水泥水化反应的进一步进行,毛细孔体系的细密程度增加。
3.2 不同含气量水泥砂浆分形维数试验结果不同含气量和龄期的水泥砂浆分形维数试验结果如表 2所示,由表 2可以看出,不同尺度孔径范围孔结构呈现不同的分形维数,①当龄期相同时,随着含气量的增加,10 000~100 000 nm孔径范围的分形维数小于3,呈现逐渐增大的趋势;1 000~10 000 nm 及100~1 000 nm孔径范围的分形维数大于3,呈现逐渐增大的趋势;<100 nm孔径范围的分形维数小于3,呈现逐渐减小的趋势。②当水泥砂浆配合比一定时,随着龄期的增大,10 000~100 000 nm 孔径范围的分形维数小于3,呈现逐渐增大的趋势;1 000~10 000 nm孔径范围的分形维数大于3,呈现逐渐减小的趋势; 100~1 000 nm孔径范围的分形维数大于3,呈现逐渐增大的趋势;<100 nm 孔径范围的分形维数小于3,呈现逐渐增大的趋势。造成不同孔径范围的孔隙呈现多种分形维数的主要原因是:由于孔的成因不同,水泥和水拌和过程中,在固、液、气三相进行混合过程中,少量气泡仍受到表面张力和液相黏度的作用;另外,拌和过程中,水会在水泥颗粒表面形成一层水膜,影响水泥颗粒的堆积。随着水泥和水之间发生物理和化学变化的进一步进行,孔隙不断被填充和细化,从而造成了水泥砂浆不同孔径范围的孔隙分形维数的差异。
| 样本编号 | 龄期/d | 孔径范围/nm | |||||||
| 10 000~100 000 | 1 000~10 000 | 100~1 000 | <100 | ||||||
| 分形维数Ds | 相关系数R2 | 分形维数Ds | 相关系数R2 | 分形维数Ds | 相关系数R2 | 分形维数Ds | 相关系数R2 | ||
| JZ | 3 | 2.301 | 0.999 4 | 3.366 | 0.994 8 | 2.948 | 0.999 6 | 2.494 | 0.999 4 |
| 7 | 2.300 | 0.998 8 | 3.056 | 0.996 0 | 3.036 | 0.995 1 | 2.563 | 0.999 8 | |
| 28 | 2.359 | 0.999 7 | 3.053 | 0.997 5 | 3.104 | 0.999 5 | 2.701 | 0.999 9 | |
| LSY1 | 3 | 2.339 | 0.999 3 | 3.448 | 0.996 7 | 2.677 | 0.998 9 | 2.474 | 1.000 |
| 7 | 2.359 | 0.999 0 | 3.313 | 0.997 2 | 2.872 | 0.998 3 | 2.581 | 1.000 | |
| 28 | 2.412 | 0.998 5 | 3.203 | 0.995 1 | 3.010 | 0.999 4 | 2.556 | 0.999 9 | |
| LSY2 | 3 | 2.209 | 0.998 5 | 3.368 | 0.995 3 | 2.689 | 0.997 5 | 2.606 | 1.000 |
| 7 | 2.293 | 0.999 0 | 3.334 | 0.996 9 | 2.739 | 0.997 6 | 2.600 | 0.999 8 | |
| 28 | 2.432 | 0.999 1 | 3.255 | 0.989 7 | 3.012 | 0.997 6 | 2.530 | 1.000 | |
| LSY3 | 3 | 2.441 | 0.998 8 | 3.468 | 0.996 7 | 2.314 | 0.998 7 | 2.634 | 0.999 4 |
| 7 | 2.495 | 0.999 3 | 3.428 | 0.996 3 | 2.411 | 0.999 4 | 2.611 | 0.995 5 | |
| 28 | 2.475 | 0.999 2 | 3.355 | 0.996 7 | 3.108 | 0.999 7 | 2.296 | 0.997 8 | |
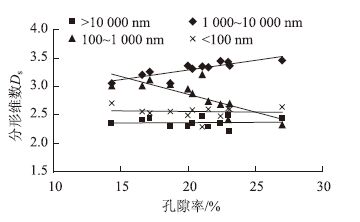
孔隙率是表征材料内部孔隙体积占其总体积百分率的物理量。 已有研究表明,孔隙率与材料的物理力学性能、耐久性能等有很密切的联系。图 6、表 3 描述了水泥砂浆不同尺度孔径分形维数与孔隙率的关系,可以看出,1 000~10 000 nm、100~1 000 nm孔径范围的分形维数与孔隙率具有良好的相关性,分别呈正相关和负相关关系,相关系数R2分别为0.712 8,0.609 4;而大于10 000 nm及小于100 nm孔径范围的分形维数与孔隙率相关性差。因而,在一定条件下可通过比较水泥砂浆1 000~10 000 nm、100~1 000 nm孔径范围的分形维数大小来推断其孔隙率大小,进而说明其内部孔隙空间分布形态复杂程度。
|
| 图 6 水泥砂浆不同尺度孔结构分形维数与孔隙率的关系 Fig. 6 Relationships between different scales' pore structure fractal dimensions and porosity of cement mortar |
| 孔径范围/nm | 回归方程 | 相关系数R2 |
| 10 000~100 000 | y=6E-05x+2.363 2 | 0.000 3 |
| 1 000~10 000 | y=0.004 9x+2.907 2 | 0.745 4 |
| 100~1 000 | y=-0.009 6x+3.609 6 | 0.719 9 |
| <100 | y=0.000 1x+2.541 9 | 0.001 3 |
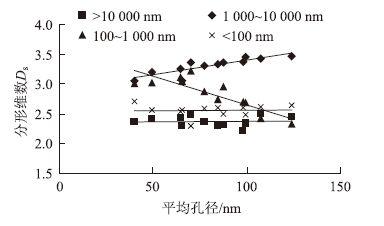
平均孔径是表示孔径平均大小的参数,其从一定方面也能够反映孔径的分布情况。一般来说,在孔隙率相同的情况下,平均孔径越小表明孔隙内部 小孔所占比例越大,反之则小孔所占比例越小。由图 7、表 4知,1 000~10 000 nm、100~1 000 nm 孔径范围的分形维数与平均孔径具有良好的相关性,分别呈正相关和负相关关系,相关系数R2分别为0.745 4,0.719 9,而大于10 000 nm及小于100 nm孔径范围的分形维数与平均孔径相关性差。因此,可以通过1 000~10 000 nm、100~1 000 nm 孔径范围的分形维数来反映水泥砂浆内部孔隙平均孔径的大小情况。平均孔径越小,孔隙内部小孔所占空间程度越高,孔结构分布形态越复杂,则分形维数越大。
|
| 图 7 水泥砂浆不同尺度孔结构分形维数与平均孔径的关系 Fig. 7 Relationships between different scales' pore structure fractal dimensions and average pore diameter of cement mortar |
| 孔径范围/nm | 回归方程 | 相关系数R2 |
| 10 000~100 000 | y=0.003 3x+2.196 1 | 0.232 8 |
| 1 000~10 000 | y=-0.005x+3.560 6 | 0.196 2 |
| 100~1 000 | y=0.015x+2.061 6 | 0.451 3 |
| <100 | y=-0.002 3x+2.670 | 0.075 1 |
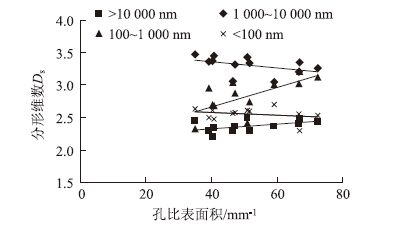
图 8、表 5表示出了水泥砂浆不同尺度孔结构分 形维数与孔隙比表面积的关系,可以看出,分形维数与孔比表面积相关性差,即水泥砂浆孔结构的复杂程度并不能用孔比表面积来表征,当水泥砂浆孔 比表面积相同时,其内部孔径分布状态可能不同,进而孔结构复杂程度也就不同。
|
| 图 8 水泥砂浆不同尺度孔结构分形维数与孔比表面积的关系 Fig. 8 Relationships between different scales’ pore structure fractal dimensions and pore specific surface area of cement mortar |
| 孔径范围/nm | 回归方程 | 相关系数R2 |
| 10 000~100 000 | y=-0.007 8x+2.508 7 | 0.874 6 |
| 1 000~10 000 | y=-0.020 7x+3.454 6 | 0.908 9 |
| 100~1 000 | y=-0.012 4x+3.225 5 | 0.55 |
| <100 | y=0.024x+2.245 | 0.689 4 |
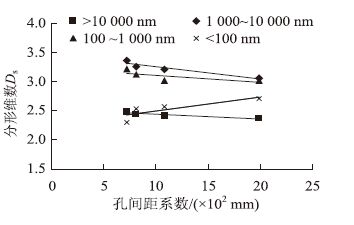
孔间距系数是指水泥石中的任一点与相邻任一气孔球面之间的最大距离,图 9、表 6描述了水泥浆体不同尺度孔结构分形维数与其孔间距系数的关系,可以看出,大于100 nm、小于100 nm孔径范围的分形维数与孔间距系数分别呈负相关性、正相关性。相比而言1 000~10 000 nm、大于10 000 nm孔径范围的分形维数与孔间距系数相关性较好,相关系数R2分别为0.908 9,0.874 6。因此,可以通过该孔径范围的分形维数来反映其孔间距系数的大小。
|
| 图 9 水泥砂浆不同尺度孔结构分形维数与孔间距系数的关系 Fig. 9 Relationships between different scales’ pore structure fractal dimensions and pore spacing coefficient of cement mortar |
| 孔径范围/nm | 回归方程 | 相关系数R2 |
| 10 000~100 000 | y=1.302 4x+2.258 3 | 0.030 7 |
| 1 000~10 000 | y=10.02x+2.460 8 | 0.685 4 |
| 100~1 000 | y=-19.034x+4.436 6 | 0.626 5 |
| <100 | y=-0.296x+2.578 7 | 0.001 1 |
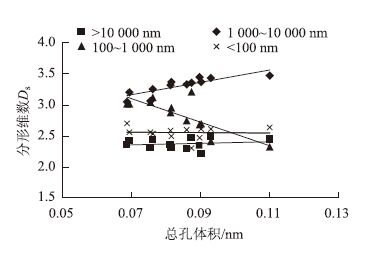
对水泥砂浆不同尺度孔结构分形维数与总孔体 积建立关系,如图 10所示。由图 10、表 7知,1 000~10 000 nm、100~1 000 nm 孔径范围的分形维数与总孔体积具有良好的相关性,分别呈正相关和负相关关系,相关系数R2分别为0.685 4,0.626 5,而大于10 000 nm及小于100 nm孔径范围的分形维数与总 孔体积相关性差。因此,可以通过1 000~10 000 nm、100~1 000 nm 孔径范围的分形维数来反映水泥砂浆内部孔隙总孔体积的大小情况。
|
| 图 10 水泥砂浆不同尺度孔结构分形维数与总孔体积的关系 Fig. 10 Relationships between different scales' pore structure fractal dimensions and total pore volume of cement mortar |
| 孔径范围/nm | 回归方程 | 相关系数R2 |
| 10 000~100 000 | y=1.302 4x+2.258 3 | 0.030 7 |
| 1 000~10 000 | y=10.02x+2.460 8 | 0.685 4 |
| 100~1 000 | y=-19.034x+4.436 6 | 0.626 5 |
| <100 | y=-0.296x+2.578 7 | 0.001 1 |
本文根据热力学分形理论模型及试验结果得到以下结论:
(1)水泥砂浆不同尺度孔结构具有多重明显的分形特征,且符合基于热力学关系的分形模型。①当龄期相同时,10 000~100 000 nm孔径范围的分形维数小于3,1 000~10 000 nm及100~1 000 nm孔径范围的分形维数大于3,随着含气量的增加均呈现逐渐增大的趋势;小于100 nm孔径范围的分形维数小于3,随着含气量的增加呈现逐渐减小的趋势。②当水泥砂浆配合比一定时,随着龄期的增大,小于100 nm、10 000~100 000 nm孔径范围的分形维数小于3,100~1 000 nm孔径范围的分形维数大于3,均呈现逐渐增大的趋势;1 000~10 000 nm孔径范围的分形维数大于3,呈现逐渐减小的趋势。
(2)不同尺度孔结构分形维数作为孔结构复杂程度的量化参数,与孔比表面积相关性极差,在1 000~10 000 nm及100~1 000 nm孔径范围内与孔隙率、平均孔径、总孔体积密切相关。相比而言,在1 000~10 000 nm孔径范围内与孔间距系数相关性最好,考虑到100~1 000 nm孔径范围孔结构所占比例较高,影响较大,可取100~1 000 nm孔径范围的分形维数来说明孔结构特性,这与采用统一的分形维数来研究孔结构特征参数的变化趋势一致。
| [1] | NAGARA T S,BANU Z.Generalization of Abrams' Law[J]. |
| [2] | MEHTA P K,BURROWS R W.Building Durable Structures in the 21st Century[J].Concrete International, 2001, 23(3):57-63. |
| [3] | SHAH S P, WANG K, WEISS W J.Mixture Proportioning for Durable Concrete:Challenges and Changes[J].Concrete International, 2000,22(9):73-78. |
| [4] | 廉惠珍,童良.建筑材料物相研究基础[M].北京:清华大学出版社,1996:105-125. LIAN Hui-zhen,TONG Liang. Basic Research on the Phase of Building Materials[M].Beijing:Tsinghua University Press, 1996:105-125. |
| [5] | 李永鑫,陈益民,贺行洋,等. 粉煤灰-水泥浆体的孔体积分形维数及其与孔结构和强度的关系[J].硅酸盐学报,2003, 31(8):774-779. LI Yong-xin, CHEN Yi-min, HE Xing-yang, et al.Pore Volume Fractal Dimension of Fly Ash-cement Paste and Its Relationship between the Pore Structure and Strength[J]. Journal of Chinese Cermaic Society, 2003, 31(8):774-779. |
| [6] | 喻乐华,欧辉,段庆普.掺珍珠岩水泥石孔分形维数及其与孔结构,强度的关系[J].材料科学与工程学报,2007,25(2):201-204. YU Le-hua, OU Hui, DUAN Qing-pu. Research on Pore Volume Fractal Dimension and Its Relation to Pore Structure and Strength in Cement Paste with Perlite Admixture[J].Journal of Materials Science and Engineering, 2007, 25(2):201-204. |
| [7] | 宋军伟,方坤河,刘冬梅,等.压汞测孔评价磷渣-水泥浆体材料孔隙分形特征的试验[J].武汉大学学报:工学版,2008,41(6):41-45. SONG Jun-wei, FANG Kun-he, LIU Dong-mei, et al.Research on Fractal Characteristics of Phosphate Slag-cement Paste Pore with MIP[J].Engineering Journal of Wuhan University, 2008, 41(6):41-45. |
| [8] | 金珊珊,张金喜,陈春珍,等.水泥砂浆孔结构分形特征的研究[J].建筑材料学报,2011,14(1):92-97. JIN Shan-shan, ZHANG Jin-xi, CHEN Chun-zhen, et al. Study of Pore Fractal Characteristic of Cement Mortar[J].Journal of Building Materials, 2011, 14(1):92-97. |
| [9] | ARANDIGOYEN M, ALVAREZ J I.Blended Pastes of Cement and Lime:Pore Structure and Capillary Porosity[J]. |
| [10] | ARANDIGOYEN M, ALVAREZ J I.Pore Structure and Mechanical Properties of Cement-lime Mortars[J]. |
| [11] | 唐明,李晓.多种因素对混凝土孔结构分形特征的影响研究[J].沈阳建筑大学学报:自然科学版,2005,21(3):232-237. TANG Ming, LI Xiao. Research of High Resistant Freezing Fly Ash Pumping Concrete in Ocean Engineering[J]. Journal of Shenyang Jianzhu University:Natural Science Edition, 2005, 21(3):232-237. |
| [12] | 王剑,张金喜.高流动混凝土孔分形特征及其与抗冻性的关系[J].混凝土,2011(12):12-15. WANG Jian, ZHANG Jin-xi. Relationship between Pore Fractal Dimension and Frost Resistance of High Fluidity Concrete[J].Concrete, 2011(12):12-15. |
| [13] | 尹红宇. 混凝土孔结构的分形特征研究[D].南宁:广西大学,2006. YIN Hong-yu. Study of Fractal Characteristic of Concrete's Pore Structure[D].Nanning:Guangxi University, 2006. |
| [14] | ZHANG Bao-qiang, LI Shao-fen. Determination of the Surface Fractal Dimension for Porous Media by Mercury Porosimetry[J]. |
| [15] | 陈三强,刘永忠,程光旭,等.用压汞法计算冻干物料的表面分形维数[J].食品科学,2004,25(7):25-29. CHEN San-qiang, LIU Yong-zhong, CHENG Guang-xu,et al. Computation on Surface Fractal Dimension of Freeze-dried Product by Mercury Porosimetry[J].Food Science, 2004,25(7):25-29. |
| [16] | 刘永忠,陈三强,孙皓.冻干物料孔隙特性表征的分形模型与分形维数[J].农业工程学报,2004,20(6):41-45. LIU Yong-zhong, CHEN San-qiang, SUN Hao. Characterizing Pores in Freeze-dried Materials by Fractal Models and Fractal Dimensions[J].Transactions of the Chinese Society of Agricultural Engineering, 2004, 20(6):41-45. |
 2016, Vol. 33
2016, Vol. 33
