扩展功能
文章信息
- 肖 杰,杨和平
- XIAO Jie, YANG He-ping
- 膨胀土堑坡格栅加筋柔性支护的数值模拟
- Numerical Stimulation of Geogrid Reinforced Flexible Support for Treating Expansive Soil Cut Slope
- 公路交通科技, 2016, Vol. 33 (6): 1-8,14
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 33 (6): 1-8,14
- 10.3969/j.issn.1002-0268.2016.06.001
-
文章历史
- 收稿日期:2015-02-09
因富含蒙脱石、伊利石或蒙脱石-伊利石混成等强亲水性矿物,膨胀土具有典型的“三性”特征,即胀缩性、裂隙性和超固结性,其工程特性受气候变化,即干湿循环作用的影响很大,导致修建于地表的各类轻型工程结构物时常发生多种破坏(病害),其中膨胀土边坡破坏地质灾害是最严重的一种类型[1, 2, 3, 4, 5]。20世纪90年代初期,南昆铁路通车运营后的前几年,百色盆地区段路堑边坡的严重破坏造成每年需花费上千万的整治费用,堪称我国膨胀土边坡在施工和营运期间最典型的破坏实例[4],而2002年开始修建的南(宁)友(谊关)高速公路施工期间宁明盆地十多公里膨胀土路段连续出现的“逢堑必滑”且多次坍滑[5]、2008年百(色)隆(林)高速公路施工中百色盆地膨胀土分布区域中心的四塘互通立交10多处匝道边坡,以及目前仍在建的南宁外环公路穿越南宁盆地膨胀土路段的多处边坡,均因施工期间处治不及时和支护技术方案不当发生了浅层坍滑破坏。
2004年长沙理工大学膨胀土课题组首创并实施土工格栅加筋柔性支护技术,成功治理南友路宁明膨胀土坍滑边坡之前,国内外工程界一直还没有找到一种既经济合理又行之有效的解决办法。最初采用土工格栅加筋柔性支护(直接用开挖膨胀土作加筋体填料)的宁明膨胀土14处坍滑堑坡经受了10年多考验,其处治效果至今仍令人十分满意。 近年来,徐晗[6]、蔡剑韬[7]、丁金州[8]等开展土工格栅加筋膨胀土渠坡的数值模拟,获得了一些有意义的成果; 笔者[9]也进行了膨胀土边坡加筋作用的对比模型试验,同样得到了有价值的结论,但土工格栅加筋稳定膨胀土堑坡真正的工作机理还不是十分清楚。
因此,本文采用FLAC2D有限差分软件,考虑降雨、蒸发等大气长期风化作用导致膨胀土抗剪强度的衰减,结合室内实测膨胀土非线性强度线确定抗剪强度参数,通过数值模拟分析研究降雨条件下风化层土体吸湿膨胀引起柔性支护膨胀土边坡土体及土工格栅的应力应变变化关系及其相互作用规律,探讨筋土界面不同强度参数、加筋层间距、坡面反包与否等因素的影响,进一步探究土工格栅加筋柔性支护处治膨胀土边坡的作用机理,弄清土工格栅对膨胀土边坡浅层坍滑破坏的抑制作用。
1 数值计算模型图 1为土工格栅加筋柔性支护膨胀土堑坡的施工设计示意图。

|
| 图 1 土工格栅加筋膨胀土边坡示意图 Fig. 1 Schematic diagram of geogrid reinforced expansive soil slope |
根据实际施工图,进行适当简化建立数值模型,见图 2,计算边坡模型高6.0 m,坡率1∶ 1.5,网格划分,共1014个网格单元。加筋体的水平宽 3.5 m,与土体风化层深度(沿坡面竖直方向2.32 m)相同,根据风化程度的不同将土体分为4层,分别为0.5,0.5,0.66 m和0.66 m。左右边界为滚动约束,底部为固定约束。

|
| 图 2 数值模型图 Fig. 2 Numerical model |
在自然气候条件作用下,随时间的推移,加筋膨胀土边坡土体含水率会因降雨、蒸发等干湿循环作用而发生变化,并伴随大量裂隙的产生,导致土体抗剪强度的不断衰减。膨胀土的饱和慢抗剪强度随法向应力的增加呈广义幂函数关系[10, 11],见式(1):

式中,Pa为大气压力; A,n,T为无量纲强度参数; SNL(σ|A,n,T)为非线性强度函数。
通过式(1)可求得任意法相应力下的切角即有效摩擦角,如式(2)所示:
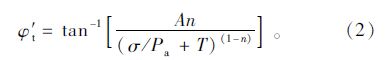
联立式(1)和式(2)可得到有效黏聚力c′ t,如式(3)所示:

在极限平衡条分法分析边坡稳定性时,因先假定滑动面,这样很容易算得土条底面的法向应力,从而可直接采用该非线性强度函数进行计算分析,但采用FLAC2D有限差分或有限元分析时,由于滑面无法事先确定而不能获得滑面的法向应力,因此无法直接应用。实际工程中,加筋土体采用重塑膨胀土回填,考虑到加筋土工格栅不仅会削弱干湿循环的作用,而且一定程度上还限制了土体的膨胀与收缩,使得土体应力与未加筋的相比会适当提高。本文仅考虑连续降大暴雨且雨强大于最外层土体的饱和渗透系数情况,忽略加筋土工格栅在一定程度上可减小降雨对加筋土体湿度变化的影响,考虑膨胀土边坡风化层内土体充分吸湿膨胀软化这一最不利状态。
实测重塑南宁膨胀土有荷干湿循环6次作用下,非线性饱和慢剪强度曲线参数A,T和n分别为0.469 1,0.035 2和0.835 2[10]。 采用其所对应法向应力5,10,20 kPa和50 kPa确定的黏聚力和摩擦角,分别为3.1 kPa、30.5°,3.4 kPa、28.6°,4.1 kPa 、26.5°和6.2 kPa、23.5°,近似代替3.5 m加筋体内4层(1~4号)土体的非线性慢剪强度参数。一般地,可认为3.5 m厚加筋体后部的原状土受外界干湿循环作用的影响很小,计算时,5号土体采用未风化原状土有荷0次得到的饱和慢剪常规抗剪强度参数,黏聚力和摩擦角为30.4 kPa和28.5°[10]。膨胀土体采用理想Mohr-Columb弹塑性本构模型来模拟,且未考虑不同深度土体弹性参数会随干湿循环作用不同而变化,均取用饱和土体的弹性参数值。
假设模型初始状态的干密度、饱和度和空隙率均相同,分别为1 700 kg/m3,54%和0.40。最上两层(1号和2号)、中间两层(3号和4号)和最里层(5号)土体的饱和渗透系数分别为2.3×10-6,2.3×10-7 m/s和2.3×10-8 m/s。实际应用时需注意将达西定律的渗透系数换算成FLAC2D中对应的“流动系数”,单位为m2/ (Pa·s),后者与前者之比约为1.02×10-4,即分别为2.346×10-10,2.346×10-11m2/ (Pa·s) 和2.346×10-12 m2/ (Pa·s)。
模型计算采用的膨胀土基本特性参数见表 1。
| 土层编号 | 干密度ρ/(kg·m-3) | 体积模量K/MPa | 剪切模量G/MPa | 热膨胀系数α/(m·K-1) | 强度参数 | |
| 黏聚力c/kPa | 内摩擦角φ/(°) | |||||
| 1 | 3.1 | 30.5 | ||||
| 2 | 3.5 | 29.6 | ||||
| 3 | 1700 | 8.710 | 2.394 | 2.34e-5 | 5.7 | 27.7 |
| 4 | 8.5 | 26.3 | ||||
| 5 | 30.4 | 28.5 | ||||
土工格栅单元采用FLAC2D中的Cable单元进行模拟,分别进行4组筋土界面参数和4组加筋间距的数值模拟计算,分析这些因素的影响规律。土工格栅及筋土界面参数详见表 2。
| 格栅 型号 | 厚度/ (×10-4 m) | 弹性模量/MPa | 界面剪切刚度/[×103(kN·m-1)] | 加筋间距/m | 界面似黏聚力/kPa | 界面似摩擦角/(°) |
| RS 35PP | 5 | 450 | 4.7 | 0.5 | 5 | 5 |
| 0.25 | ||||||
| 0.5 | 10 | 10 | ||||
| 0.75 | ||||||
| 1.0 | ||||||
| 0.5 | 15 | 15 | ||||
| 0.5 | 20 | 20 |
缪协兴[12]提出了湿度应力场理论,认为可用热传导形成的温度应力场近似代替水渗透导致的湿度应力场。因此,可根据温度场与湿度场的相似性,由室内无荷膨胀量试验结果,再通过数值模拟的方法来获得热膨胀系数。采用加筋土体的热膨胀系数为2.34×10-5 m/K,设初始含水率时的温度为0 ℃,吸水完全膨胀后的温度为200 ℃[13]。5号土体的含 水率受外界降雨影响很小,可将其设为0 ℃,最表层设为200 ℃,计算得到坡体湿度场的等效温度场变化见图 3。加筋体应力应变计算时,先设置cable单元,再施加温度场。

|
| 图 3 坡体湿度场的等效温度场变化 Fig. 3 Equivalent temperature field change of slope humidity field |
首先,开展加筋与未加筋膨胀土边坡的数值模拟分析,探讨加筋的作用效果。其中,加筋边坡坡面未反包,格栅加筋间距0.5 m,长3.5 m,界面似黏聚力和摩擦角分别为10 kPa和10 ℃。
图 4和图 5分别为计算得到的未加筋边坡的水平位移和强度折减后的最大剪应变增量与安全系数示意图。由图可知,未加筋边坡的最大水平位移达到1.25 m,安全系数为0.86,滑面深度约为1.5 m,表明未加筋边坡在干湿循环作用下,随膨胀土体的抗剪强度不断下降,遇持续降雨后发生了浅层坍滑破坏。

|
| 图 4 未加筋边坡的水平位移 Fig. 4 Horizontal displacement of unreinforced slope |

|
| 图 5 未加筋边坡的最大剪应变增量及安全系数 Fig. 5 Maximum shear strain increment and safety factor of unreinforced slope |
图 6~图 8分别为加筋边坡的格栅轴力、坡面水平位移和最大剪应变增量及安全系数示意图。由图可以发现,水平格栅的最大轴力随高度的增加,先增加后减小,其中第6层的最大轴力为2.545 kN; 水平格栅最大轴力的出现位置与未加筋边坡的滑动面位置基本一致,约位于格栅2/3处(至坡面距离); 加筋边坡坡面的最大水平位移仅1.80 cm,距坡脚高1.5 m,与未加筋边坡相比,显著减小; 加筋边坡的安全系数为1.17,而最危险滑动面位置由素膨胀土边坡的浅层移动到了格栅后部。因此,土工格栅与加筋土体间的相互作用,有效地约束了边坡的水平位移,一定程度上减小了土体的吸湿膨胀软化效应,间接提高了其强度,使得最危险滑动面向坡体深部转移。

|
| 图 6 加筋边坡格栅的轴力分布 Fig. 6 Axial force distribution of geogrid on reinforced slope |

|
| 图 7 加筋边坡坡面的水平位移 Fig. 7 Horizontal displacement of reinforced slope surface |

|
| 图 8 加筋边坡的最大剪应变增量及安全系数 Fig. 8 Maximum shear strain increment and safety factor of reinforced slope |
图 9为不同界面参数加筋边坡格栅的轴力分布,其中似黏聚力和似摩擦角为10 kPa和10 ℃的见图 6。图 10为不同界面参数加筋边坡坡面水平位移。

|
| 图 9 不同界面参数加筋边坡格栅的轴力分布 Fig. 9 Axial force distribution of geogrids on reinforced slopes with various interface parameters |

|
| 图 10 不同界面参数加筋边坡坡面水平位移 Fig. 10 Horizontal displacement of surface of reinforced slopes with various interface parameters |
为便于对比,绘制了每层格栅的最大轴力随高度的变化见图 11。由图易知,界面强度参数由小到大变化时,格栅最大轴力(界面参数从小到大)分别为2.768,2.545,2.545 kN和2.499 kN,出现在第4层(高0.5 m)、第6层(高1.5 m)、第6层(高1.5 m)和第7层(高2.0 m),最大与最小值之差仅为0.269 kN,且格栅最大轴力沿高度的变化曲线基本重合(最小的除外); 坡面最大水平位移分别为2.19,1.80,1.80 cm和1.75 cm,位置均位于高度约1.5 m处,且坡面水平位移随高度的变化曲线也基本重合(最小的除外); 安全系数分别为1.08,1.17,1.24和1.31,但最危险滑动面位置相同,且有效剪应力分布大体相同,最大值均出现在坡脚处,约为20 kPa。由此可知,格栅的最大轴力受筋土界面参数的影响很小,当界面强度参数大于某值后,其大小的改变对加筋格栅的应力、加筋体内土体的应力场以及边坡位移的影响均很微小,但安全系数会随界面强度的增大而不断增大。值得注意的是,即便筋土界面参数的似黏聚力和似摩擦角分别为5 kPa 和5 °时,大暴雨3天且不考虑格栅对渗透性及土体强度的增强作用情况下,安全系数也有1.08,仍大于1.0,未处于极限平衡状态,表明格栅的存在能显著提高边坡的稳定性。

|
| 图 11 不同界面参数格栅最大轴力随高度的变化 Fig. 11 Maximum axial force of geogrid with various interface parameters varying with height |
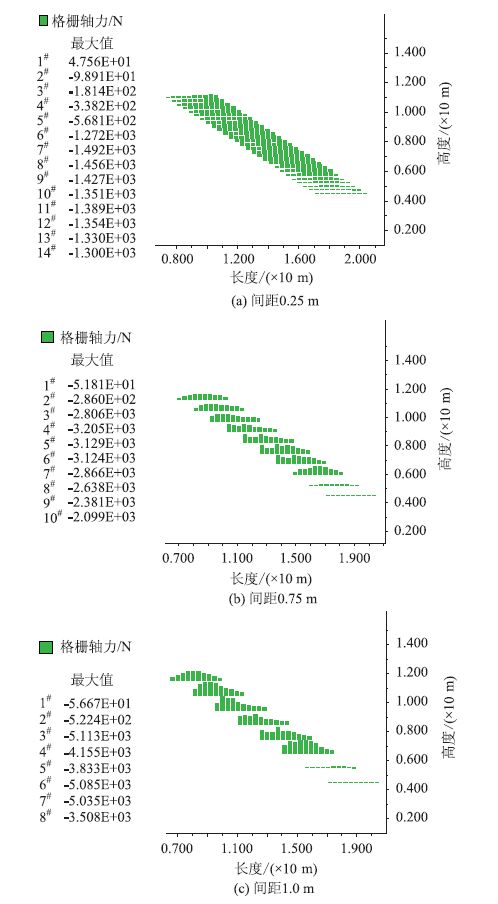
图 12~图 14分别为不同加筋间距边坡格栅轴力分布、坡面水平位移和格栅最大轴力随高度的变化图,其中加筋间距为0.5 m的轴力分布见图 6。
|
| 图 12 不同加筋间距边坡格栅的轴力分布 Fig. 1 Axial force distribution of geogrids with various reinforcement spacings |

|
| 图 13 不同加筋间距加筋边坡坡面水平位移 Fig. 13 Horizontal displacement of surface of reinforced slope with various reinforcement spacings |
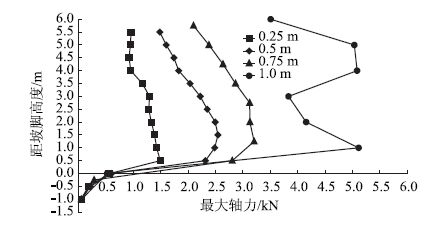
|
| 图 14 不同加筋间距格栅最大轴力随高度的变化 Fig. 14 Maximum axial force of geogrid with various reinforcement spacings varying with height |
分析图易知,不同加筋间距条件下,各层格栅的最大轴力沿高度的变化规律基本相同,先增加后减小,且加筋间距越小,其最大值越小,如加筋间距为0.25,0.5,0.75 m和1.0 m的4种边坡格栅最大轴力分别为1.499,2.545,3.235 kN和5.3 kN; 坡面水平位移随高度的增加均呈先增大后减小的规律变化,且加筋间距越大,其值越大,当加筋间距由0.25 m变至0.75 m时,两两间位移变化差值较一致,但由0.75 m增加为1.0 m时,位移差值变化很大,由不同加筋间距(由小到大)的最大值分别为1.17,1.80,2.43 cm和4.75 cm也可轻易看出; 安全系数随加筋间距的增加而减小,分别为1.33,1.17,1.11和1.06,最危险滑动面位置基本一致。因此,加筋间距对膨胀土边坡稳定性的影响较大,间距越小,边坡的稳定性越好。究其原因可能是一方面加筋间距越小,边坡被分割的层位越多,加筋土体的厚度越小,土体吸湿膨胀软化的作用越小;另一方面随土工格栅数量的增加,其受力越小,整体性越好,限制边坡水平变形的能力增强。但对实际工程而言,并非是加筋间距越小越好,还需结合实际工程特性、施工的可操作性和经济性等因素综合确定加筋间距。
3.4 有无反包格栅的影响因加筋膨胀土边坡施工中将土工格栅进行逐层反包,每层预留一定长度格栅再通过连接棒与上层格栅进行连接,并用“U”形钉在尾部将格栅固定,使加筋体形成一个整体发挥作用,但反包格栅的力学响应如何,也需要研究。因此,开展筋土界面强度参数似黏聚力和似摩擦角分别为10 kPa和10°,加筋间距0.5 m,坡面反包格栅加筋边坡数值模拟,并与未反包情况进行了对比分析,研究其作用效果。
图 15给出了反包边坡的水平加筋格栅轴力分布。图 16为反包与未反包加筋边坡坡面的水平位移。分析以上两图,并与未反包边坡结果(见图 12(b))进行对比,可知水平格栅的最大轴力随高度的变化规律基本一致,最大值也出现在第6层,为2.519 kN,略小于未反包的2.545 kN; 反包格栅的最大轴力为0.514 kN,出现在坡脚处,使得近坡面的水平格栅轴力变大,但最大轴力略有减小; 最大水平位移的位置相同,但值稍有变小(1.75 cm),安全系数也相同均为1.17。因此,与未反包加筋相比,反包土工格栅使坡面附近水平格栅轴力略有增加,边坡的水平位移稍有减小。究其原因应该是,水平格栅加筋后,边坡最危险滑动面已由浅层推移至加筋体后部,此时可将加筋体视为一个整体,反包格栅改变了加筋体内水平格栅及土体应力状态,使加筋体的整体性更强,“框箍”作用更好,保证了加筋体的稳定。此时,对边坡稳定性起决定作用的已变为加筋体后土体的强度。另一方面,反包格栅具有有效的防护作用,可有效降低降雨和蒸发等干湿循环作用对加筋土体的影响。且当表层土体吸湿膨胀时,限制边坡水平膨胀能力较未反包要稍强,可进一步减小深部土体受外界干湿循环的影响,使加筋体深部土体强度不会下降或下降程度有限,从而间接提高了边坡的稳定性,确保其稳定,这与文献[9]中室外大型模型试验结果相一致。

|
| 图 15 反包加筋边坡坡面的轴力分布 Fig. 15 Axial force distribution on surface of enveloped reinforced slope |

|
| 图 16 反包与未反包加筋边坡坡面的水平位移 Fig. 16 Horizontal displacement of surfaces of enveloped and unenveloped slopes |
针对在干湿循环作用下,膨胀土边坡常发生浅层坍滑这一特性,采用土工格栅加筋柔性支护技术进行处治,取得了良好的效果。加筋土工格栅一方面将边坡坡体进行了有效分割,加筋后边坡土体的裂隙发展深度受到限制,每层的裂隙最深也仅为加筋体间距的距离,如加筋间距为0.5 m时,加筋坡体裂隙的连续开展深度均不会大于0.5 m,这是由于土工格栅的存在阻碍了裂隙的进一步扩展。因此在干湿循环作用下,加筋边坡土体的裂隙不会像自然边坡或素膨胀土边坡那样开展,能达到弱风化与未风化层界面处; 另一方面土工格栅还起着“保湿防渗”作用,可以减少环境干湿循环作用对边坡土体的影响,保持土体含水量的稳定,从而保证土体具有相对较高的强度,同时还可以减轻干缩裂缝的产生。另外,由于土工格栅在加筋体中发挥良好的“框箍”作用,一定程度上限制了土体的膨胀、防止其崩解,使得加筋体成为一个整体,形成一个很厚的支护体,且因加筋坡体的坡率一般较缓,可保证支护体自身不会发生破坏。支护体具有一定的重量,相当于给处治边坡土体施加了一定的附加压力,可有效地限制加筋体后坡土体的吸湿膨胀,保持其强度不会发生大的衰减,从而保证了处治膨胀土边坡的稳定。因此,土工格栅加筋柔性支护能有效地解决膨胀土边坡的浅层破坏。
5 结论(1)土工格栅与加筋土体间的相互作用,有效地约束了边坡的水平位移,一定程度上减小了土体的吸湿膨胀软化效应,使得可能滑动面向坡体深部转移。
(2)格栅最大轴力受筋土界面参数的影响很小,当界面强度参数大于某值后,其大小的改变对加筋格栅的应力、加筋体内土体的应力场以及边坡位移的影响均很微小,但安全系数会随界面强度的增大而不断增大; 即便筋土界面参数较小,边坡中只要加入格栅,就能显著提高其稳定性。
(3) 不同加筋间距条件下,各层格栅的最大轴力沿高度的变化规律基本相同,先增加后减小,且加筋间距越小,其最大值越小; 加筋间距对膨胀土边坡稳定性有较大影响,间距越小,边坡的稳定性越好。
(4)反包土工格栅使坡面附近水平格栅轴力略有增加,边坡的水平位移稍有减小,可间接提高边坡的安全系数,以及坡面的耐冲刷和边坡的整体性。
| [1] | 廖世文. 膨胀土与铁道工程[M]. 北京:中国铁道出版社, 1984. LIAO Shi-wen. Expansive Soil and Railway Engineering[M]. Beijing:China Railway Publishing House, 1984. |
| [2] | 李生林, 秦素娟, 薄遵昭, 等. 中国膨胀土工程地质研究[M]. 南京:江苏科学技术出版社, 1992. LI Sheng-lin, QIN Su-juan, BO Zun-zhao, et al. Chinese Expansive Soil Engineering Geological Studies[M]. Nanjing:Jiangsu Science and Technology Publishing House, 1992. |
| [3] | 曲永新, 张永双, 杨俊峰, 等. 中国膨胀性岩、土一体化工程地质分类的理论与实践[M]//中国工程地质五十年. 北京:地震出版社, 2000:140-164. QU Yong-xin, ZHANG Yong-shuang, YANG Jun-feng, et al. Theory and Practice of Classification of Chinese Integrative Expansive Rock Soil Engineering Geology[M]//Fifty Years for Chinese Engineering Geology. Beijing:Seismological Press, 2000:140-164. |
| [4] | 冯玉勇, 张永双, 曲永新,等. 南昆铁路百色盆地膨胀土路堤病害机理研究[J]. 岩土工程学报, 2001, 23(4):463-467. FENG Yu-yong, ZHANG Yong-shuang, QU Yong-xin, et al. Mechanism of Embankment Defects Caused by Expansive Soils in Baise Basin, Nankun Railway[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4):463-467. |
| [5] | 杨和平, 郑鹏. 南友路膨胀土堑坡滑坍的地质调查与思考[J]. 长沙理工大学学报:自然科学版,2004, 1(1):14-19. YANG He-ping, ZHENG Peng. Geological Investigation and Reflection on the Expansive Soil in Nanning-Youyiguan Highway[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2004, 1(1):14-19. |
| [6] | 徐晗, 汪明元, 黄斌, 等. 土工格栅加筋膨胀土渠坡数值模拟研究[J]. 岩土力学, 2007, 28(增1):599-603. XU Han, WANG Ming-yuan, HUANG Bin, et al. Numerical Stimulation Research on Canal Slope of Expansive Soil Strengthened by Geogrid[J]. Rock and Soil Mechanics, 2007, 28(S1):599-603. |
| [7] | 蔡剑韬, 汪明元, 周小文, 等. 吸湿条件下土工格栅加筋膨胀土边坡稳定分析[J]. 人民长江, 2008, 39(11):84-88. CAI Jian-tao, WANG Ming-yuan, ZHOU Xiao-wen, et al. Analysis of Expansive Soil Slope Stability Reinforced by Geogrid under Condition of Moisture Absorption[J]. Yangtze River, 2008, 39(11):84-88. |
| [8] | 丁金华. 膨胀土边坡浅层失稳机理及土工格栅加固处理研究[D]. 杭州:浙江大学, 2014. JING Jin-hua. Research on Mechanism of Shallow Instability of Expansive Soil Slope and Geogrid-confined Effect on Swelling Deformation[D]. Hangzhou:Zhejiang University, 2014. |
| [9] | 肖杰, 杨和平, 符浩, 等. 膨胀土边坡加筋作用的对比模型试验[J]. 中国公路学报, 2014, 27(7):24-31. XIAO Jie, YANG He-ping, FU Hao, et al. Comparison Model Test on Effect of Geogrid Reinforcement for Expansive Soil Slope[J]. China Journal of Highway and Transport, 2014, 27(7):24-31. |
| [10] | 肖杰, 杨和平, 王兴正, 等. 南宁外环膨胀土抗剪强度非线性特征及影响因素分析[J]. 中国公路学报, 2014, 27(10):1-8. XIAO Jie, YANG He-ping, WANG Xing-zheng, et al. Analysis of Nonlinear Characteristics of Shear Strength of Nanning Expansive Soil and Its Influencing Factors[J]. China Journal of Highway and Transport, 2014, 27(10):1-8. |
| [11] | LADE P V. The Mechanics of Surficial Failure in Soil Slopes[J]. |
| [12] | 缪协兴,杨成永,陈至达. 膨胀岩体中的湿度应力场理论[J]. 岩土力学,1993, 14(4):49-55. MIAO Xie-xing, YANG Cheng-yong, CHEN Zhi-da. Humidity Stress Field Theory in Swelling Rock Mass[J]. Rock and Soil Mechanics, 1993, 14(4):49-55. |
| [13] | 程斌. 考虑格栅反包的加筋膨胀土边坡稳定性数值模拟分析[D]. 长沙:长沙理工大学, 2012, 30-32. CHENG Bin. Numerical Simulation Analysis on Stability of Turnup Geogrid Flexible Supporting Expansive Soil Slope[D]. Changsha:Changsha University of Science and Technology, 2012, 30-32. |
 2016, Vol. 33
2016, Vol. 33
