扩展功能
文章信息
- 马靖莲, 任建伟, 于丽静, 沈丽
- MA Jing-lian, REN Jian-wei, YU Li-jing, SHEN Li
- 乳品冷链物流系统建模研究
- Study on Modeling of Dairy Product Cold Chain Logistics System
- 公路交通科技, 2016, 33(5): 153-158
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 153-158
- 10.3969/j.issn.1002-0268.2016.05.024
-
文章历史
- 收稿日期:
2. 内蒙古大学 交通学院, 内蒙古 呼和浩特 010070 ;
3. 烟台南山学院, 山东 烟台 265700 ;
4. 山东交通学院, 山东 济南 250037
2. College of Transportation, Inner Mongolia University, Hohhot Inner Mongolia 010070, China ;
3. Yantai Nanshan University, Yantai Shandong 265700, China ;
4. Shandong Jiaotong University, Jinan Shandong 250037, China
乳品冷链物流是食品物流行业中重要的组成部分。中国乳制品工业协会的研究显示:2020年前中国乳品人均占有量可望赶上当下亚洲人均占有量的平均水平,即每人每年40 kg,我国乳品总产量将居世界第3位。由此可见,我国乳品市场具有十分广阔的发展空间。
乳品在加工、储藏、运输及销售过程中,都必须始终处于受控的低温状态,一旦某一环节出现问题后果不堪设想。乳品冷链物流的运作情况直接影响到人民群众的营养、健康和安全。近些年来,国内外有许多学者都针对冷链物流展开了研究。国外研究冷链物流的重点是冷链的技术环节,即对冷藏和冷冻技术方法的研究。Hallie Forcinio和Carol Casper等认为冷链运输可以改善供应链效率,而温度控制是冷链运输中最棘手的问题[1-2];James等对食品运输模型进行了总结回顾,并提出温度是保持食品品质新鲜的关键[3];Ju-Chia Kuo等构建了考虑多温度控制节点的食品冷链物流分派模型[4];Victoria等人构建了将食品运输到发展中国家的冷链物流系统[5]。中国的冷链物流始于20世纪中叶,目前已取得了丰富的成果。刘海波认为冷链物流对保障食品品质、提高食品安全具有重要作用[6] ;何明柯设计了冷链系统框架结构的评估程序,并界定了冷链系统的基础结构[7];汪旭晖和张其林研究了基于物联网的生鲜农产品冷链物流体系[8];崔忠付回顾了2015年中国冷链物流的发展情况,并认为2016年中国的冷链物流将继续走高[9];姚乐对乳品冷链物流外包的意义和风险进行了分析[10];王瑞霞以我国内蒙古自治区为例介绍了生鲜乳及其制品冷链物流的现状,并提出了改进措施,包括应健全关于冷链物流的法律法规标准和加快完善第三方冷链物流业的建设体系[11]。由文献分析可知,虽然冷链物流研究成果丰富,但是对乳品冷链物流的研究还很少(以“乳品”和“冷链物流”为关键字在CNKI中搜索,仅能搜到5篇文章),尚没有文献对冷链物流系统进行系统的建模研究。
因此本文将以乳品冷链物流为研究对象,系统地对乳品冷链物流系统进行建模研究。该研究是制订乳品冷链物流行业操作技术规范的理论基础,具有重要的理论价值,也对提高乳品冷链物流服务水平、保证乳品的高度新鲜和品质营养安全有重要的指导作用,具有重要的现实意义。
1 乳品冷链物流系统的界定所谓乳品冷链物流是指:乳品在生产、加工、储藏、运输配送、销售、消费等各个环节中始终处于规定的低温环境下,以保证乳品品质新鲜,减少乳品损耗的一项系统工程。乳品种类繁多(如图 1所示),不同学者对乳品有不同的定义和分类。本文所指乳品冷链物流重点是指嗜酸乳和巴氏杀菌乳等乳制品的冷链物流,不包括冰淇淋类和干酪类,也不包含常温乳品(如乳粉类)。
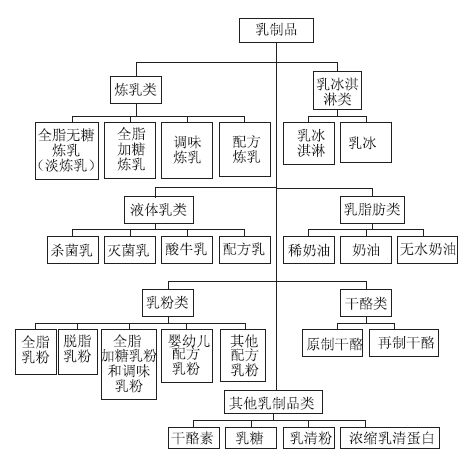
|
| 图 1 乳品分类 Fig. 1 Classification of dairy products |
| |
乳品的最终质量主要取决于在冷藏链中储藏和流通的时间(Time)、温度(Temperature)、及产品耐藏性(Tolerance),因此乳品冷链物流需遵循 “3T原则”。“3T原则”指出了乳品的品质维持所允许的时间和温度之间存在一定的关系,并且还指出了乳品在流通中因时间-温度的变化会引起品质降低的累积和品质降低的不可逆。因此对时间-温度之间微妙关系的研究是本文构建乳品冷链物流系统模型的主要目标。乳品冷链物流的体系结构包含生产、加工、储藏、运输配送、销售、消费等环节,如图 2所示。该体系结构可抽象为如图 3所示的乳品冷链物流系统基本流程。本文对乳品冷链物流系统的建模即以图 3所示流程为基础。在模型构建过程中,本文用i表示研究对象(乳品)的类别,n表示该类乳品的数量,节点j表示中间环节的处理器。所谓处理器就是指对研究对象进行加工处理的系统,如冷藏仓库系统、运输系统、以及销售单元系统。
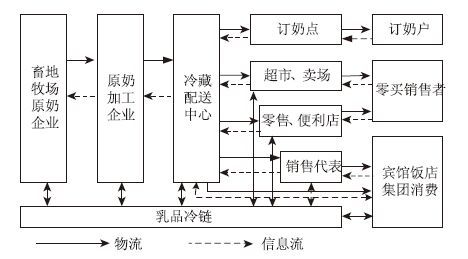
|
| 图 2 乳品冷链物流系统体系结构 Fig. 2 Dairy product cold chain logistics system architecture |
| |
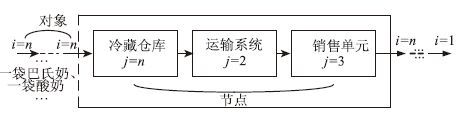
|
| 图 3 乳品冷链物流系统基本流程 Fig. 3 Basic flowchart of dairy product cold chain logistics system |
| |
2 基本假设
(1) n个对象遵循一定的随机概率分布依次进入节点j=1。
(2) n个对象在节点j=2和节点j=3中的运行时间遵循一定的随机概率分布。
(3) 每个节点在容量允许的范围内可同时有序处理多个对象。
(4) 每个节点遵循先进先出原则。
(5) 因为冷链中乳品的温度比较低,所以每个节点中对象之间的热传递可以忽略不计。
(6) 因为冷链中乳品的温度比较低,所以对象进出节点时造成的热量损失可以忽略不计。
3 乳品冷链物流系统模型构建本文将采用多目标随机规划的方法来构建乳品冷链物流系统模型,主要内容包括4方面:决策变量的选取、目标函数的设定、系统运行的描述和约束条件的建立。
3.1 选取决策变量根据乳品冷链物流系统的运行条件,模型的决策变量基于系统节点的物理属性和乳品在系统运行中的物流属性选出,有关物理属性的决策变量用 ω表示,有关物流属性的决策变量用π表示。因此可将决策变量θ表示为:
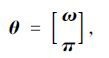
|
(1) |
式中根据物理属性选取出的决策变量是对物流成本和乳品的新鲜程度有重大影响力的节点制冷力Φj;根据乳品在系统运行中的物流属性选取出的决策变量是对象到达节点的时间ti和对象在节点中的运行时间Tij。具体表示如下:
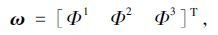
|
(2) |
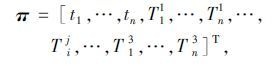
|
(3) |
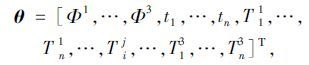
|
(4) |
式中,Φj为节点j的制冷力;ti为对象i进入系统的时间;Tij为对象i在节点j中运行的时间。
根据决策变量里的确定性因素和不确定性因素,可以把决策变量θ分为确定性决策变量θc和不确定性决策变量θuc。确定性决策变量θc又称可控决策变量,是指在系统运行过程中管理人员可以直接控制的变量,如每个节点j的制冷力Φj和冷藏仓库系统节点内每个对象的运行时间Ti1。不确定性决策变量θuc又称不可控变量,是指在系统运行过程中管理人员不可以直接控制的变量或不能直接访问得到的变量,如对象i进入系统的时间ti、运输系统节点内对象i的运行时间Ti2以及销售单元系统节点内对象i的运行时间Ti3。一般来说,对象i进入系统的时间间隔服从均匀分布,对象i在运输系统和销售单元系统中的运行时间服从高斯分布。具体表示如下:
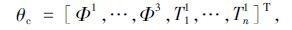
|
(5) |
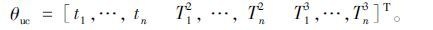
|
(6) |
乳品冷链物流系统的目标函数主要有:乳品质量Q(θ)最高,即对象i的温度尽量控制在保障乳品品质最优的温度范围内;物流成本C(θ)最少,即节点j中因制冷所花费的成本尽量少;运行时间T(θ)最短,即实际交货时间最短,也就是说对象i离开销售单元节点j=3的时间尽量短。具体表示如下:
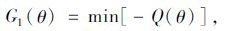
|
(7) |
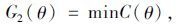
|
(8) |
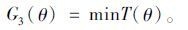
|
(9) |
在该目标函数中,T(θ)与Q(θ)是相互有利的,因为当交货时间最短时,乳品的品质也会最新鲜;而C(θ)与Q(θ)是相互制约的,因为要想实现高质量,制冷成本不可能最低。为便于求解,可将该多目标决策问题转化为单目标决策问题,如式(10)所示:
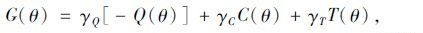
|
(10) |
式中,γQ,γC,γT分别为函数Q(θ),C(θ),T(θ)的加权系数。为了让3个目标在目标函数中占有合理的比重,可以取加权系数γQ,γC,γT分别设为函数Q(θ),C(θ),T(θ)期望值的倒数。
3.3 描述系统运行乳品冷链物流系统是一个混合的动态系统,所谓的混合是指它同时包含离散事件系统和连续时间系统两种状态[12-14]。
3.3.1 离散事件系统在乳品冷链物流系统中,系统的任意对象离开所在节点时,对象与节点的物流属性都随时间发生了跳跃性间断的状态变化,因此它属于离散事件系统状态变量。每一个对象i和节点j的状态发生改变时都会对应着一个事件时间点,本文设这个时间点集为τ。因为本系统中对象个数为n,节点个数为3,所以这是一个n×4的向量矩阵,表示如下:

|
(11) |
式中,每个事件时间点τij代表对象i离开节点j的时间。由此易知:
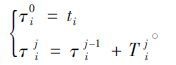
|
(12) |
离散的对象状态pi(a),即a时刻对象i所在的节点,表示如下:
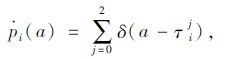
|
(13) |
式中狄拉克δ函数,当自变量≥0时,函数值为1,否则函数值为0。
离散的节点状态nj(a),即a时刻节点j中的对象数量,表示如下:
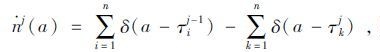
|
(14) |
式中狄拉克δ函数,当自变量≥0时,函数值为1,否则函数值为0。
显然,以上两个变量pi(a)和nj(a)的值都是整数,并且pi(a)是个单调非减的时间函数。nj(a)表示当对象i进入该节点j时,该节点j中的对象数量即增加;同理,当任意对象k离开该节点j时,该节点j中的对象数量即减少。
3.3.2 连续时间系统在乳品冷链物流系统中,对象与节点的物理属性——温度一直在随着时间做连续变化,因此它属于连续时间系统状态变量。设对象i的连续时间状态变量为yi(a),它表示a时刻对象i的温度;设节点j的连续时间状态变量为uj(a),它表示a时刻节点j的温度。对象i的温度函数yi(a)用二阶状态空间模型可表示为:
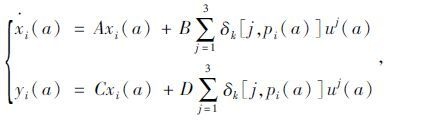
|
(15) |
式中,A,B,C,D均为方程参数。xi(a)表示对象i与节点环境相互作用的状态变量,是中间变量。δk[j,pi(a)]表示克罗内克δ函数:当a时刻对象i在节点j时,函数值为1,否则函数值为0。
节点j的温度函数uj(a), 用热传递方程表示如下:
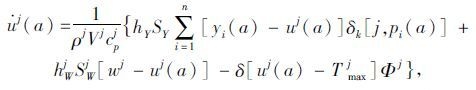
|
(16) |
式中,ρj为节点j内空气密度;Vj为节点j内空气体积;cpj为节点j内空气比热容;hY为对象表面热传递系数,考虑周围空气流动和速度产生的影响;SY为对象的平均表面积;hWj为节点j外表面热对流传递系数;SWj为节点j的外表面积;wj为节点j的外部温度,是一个不确定性因素;Tmaxj为节点j内温度的临界值。
3.4 建立约束条件在实际的乳品冷链物流系统中,冷藏仓库系统、运输系统、销售单元系统的容量都是有限的。设节点j的容量为Cj,则Cj>0且有限。如果对象i已经完成了在节点j中的活动,但是节点j+1中对象的数量已经达到了节点j+1的最大容量,那么对象i就必须得在节点j中继续等待,直到等到节点j+1中有了空余位置,对象i方可进入。为了更好地表达这样的约束条件,定义了一个实际运行时间函数Sij,具体表示如下:
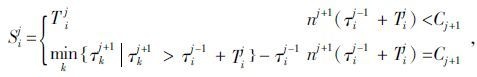
|
(17) |
式中,Sij表示对象i在节点j内的停留时间。由上述公式易知,当对象i已经完成了在节点j中的活动,如果节点j+1中对象的数量仍然未处于饱和状态,那么对象i就可以顺利进入下一节点即节点j+1内,此时Sij=Tij。
约束条件(一)质量函数:Q(θ)函数是从乳品的品质出发来衡量系统目标。设乳品质量允许的最高温度为TH,乳品质量允许的最低温度为TL。对于乳品来说,温度偏高和温度偏低都不利于乳品质量的保证,但是温度偏高比温度偏低更能使乳品的质量下降。设Γ(x)表示对象i的温度与质量之间的函数关系,设交货时的乳品温度yi(τi3)表示乳品的最终质量,则:
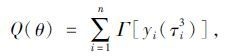
|
(18) |
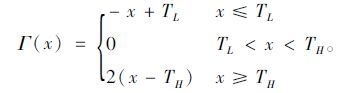
|
(19) |
约束条件(二)成本函数:C(θ)函数是从成本出发来衡量系统目标。在本文的乳品冷链物流系统中,节点j的制冷力Φj是成本的唯一决定因素。式中φj表示预期的制冷力:
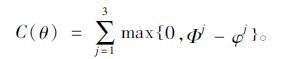
|
(20) |
约束条件(三)时间函数:T(θ)函数是从乳品的实际交货期与预期交货期之间的差距出发来衡量系统目标。在本文的乳品冷链物流系统中,事件时间点τi3即是乳品的实际交货期,它决定着整个系统的运行时间,式中di表示预期交货期,则
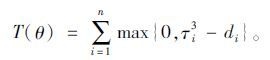
|
(21) |
综上可得出本文乳品冷链物流系统的多目标随机规划模型为式(22):
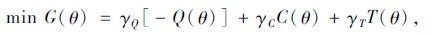
|
(22) |
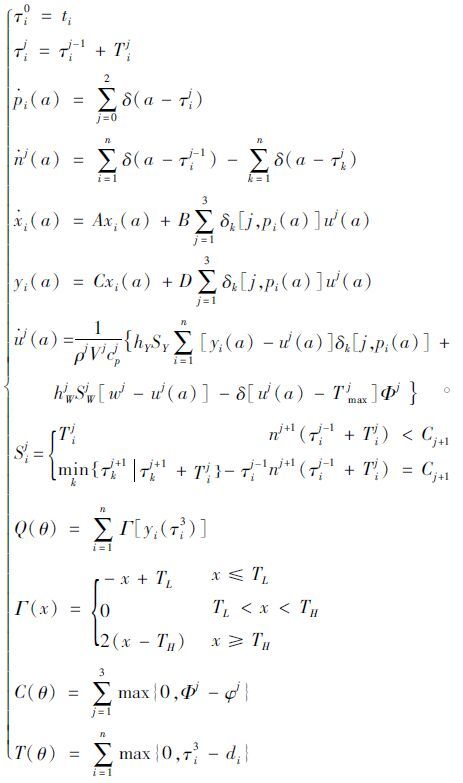
|
乳品冷链物流在我国还处于起步阶段,无论是设备设施、技术标准还是管理体制、服务水平等方面都需要进一步完善和发展。本文首先界定了乳品冷链物流的研究范畴,即酸乳和巴氏杀菌乳等乳制品的冷链物流;然后分析了乳品冷链物流系统的体系结构,该体系结构包含生产、加工、储藏、运输配送、销售、消费等环节,并在此基础上抽象出了乳品冷链物流系统基本流程;最后基于混合动态系统的建模方式,构建了乳品冷链物流系统随机规划模型,该模型以质量最高、物流成本最低、运行时间最短为目标函数,以物理属性和物流属性为决策变量,以节点容量为约束条件,能够平衡乳品冷链物流成本、交货期和质量三者的关系,帮助企业提供低成本、高水平的乳品冷链物流服务。乳品冷链物流是冷链物流的重要分支,然而目前我国有关该领域的研究还非常少,而对其进行定量研究的几乎没有,希望有更多的专家学者能开展这方面的研究,为我国乳品冷链物流的发展贡献智慧,为我国人民食品安全提供保障。
| [1] | FORCINIO H, WRIGHT C. Cold Chain Concerns[J]. Pharmaceutical Technology, 2005, (5) : 44–50 . |
| [2] | CASPER C. Safety Starts with Temperature Control[J]. Food Logistics, 2007, (12) : 16–20 . |
| [3] | JAMES S J, JAMES C, EVANS J A. Modeling of Food Transportation Systems: a Review[J]. International Journal of Refrigeration, 2006, 29 (6) : 947–957 . |
| [4] | KUO J C, CHEN M C. Developing an Advanced Multi-temperature Joint Distribution System for the Food Cold Chain[J]. Food Control, 2010, 21 (4) : 559–566 . |
| [5] | SALIN V. A Cold Chain Network for Food Exports to Developing Countries[J]. International Journal of Physical Distribution & Logistics Management, 2003, 33 (10) : 918–933 . |
| [6] | 刘海波. 北京市食品冷链物流配送研究[J]. 冷藏技术,2009, (4) :11–14. LIU Hai-bo. Research of Food Cold Chain Logistics Distribution in Beijing[J]. Cold Storage Technology, 2009, (4) : 11–14 . |
| [7] | 何明坷. 冷链系统基础结构评价指标体系研究[J]. 北京商学院学报,2001,16 (2) :46–50. HE Ming-ke. Research of Cold Chain System Infrastructure Evaluation Index System[J]. Journal of Beijing Institute of Business, 2001, 16 (2) : 46–50 . |
| [8] | 汪旭晖, 张其林. 基于物联网的生鲜农产品冷链物流体系构建:框架、机理与路径[J]. 南京农业大学学报:社会科学版,2016,16 (1) :31–41. WANG Xu-hui, ZHANG Qi-lin. Construction of Cold Chain Logistics System for Fresh Agricultural Products Based on Internet of Things: Framework,Mechanism and Path[J]. Journal of Nanjing Agricultural University:Social Sciences Edition, 2016, 16 (1) : 31–41 . |
| [9] | 崔忠付. 新常态下的冷链物流[J]. 中国物流与采购,2016, (4) :38–39. CUI Zhong-fu. Cold Chain Logistics under the New Normal Condition[J]. China Logistics & Purchasing, 2016, (4) : 38–39 . |
| [10] | 姚乐. 乳品冷链物流外包运作的探讨[J]. 物流科技,2008,31 (9) :51–53. YAO Le. The Discussion on Outsource Operation of Diary Industry Cold China[J]. Logistics Sci-Tech, 2008, 31 (9) : 51–53 . |
| [11] | 王瑞霞.内蒙古生鲜乳及其制品冷链物流研究[D]. 呼和浩特:内蒙古农业大学,2012. WANG Rui-xia. Study on Cold Chain Logistics of Fresh Milk and Its Products in Inner Mongolia[D]. Hohhot:Inner Mongolia Agricultural University,2012. |
| [12] | 陈向勇, 井元伟, 李春吉. 基于Lanchester方程的作战混合动态系统最优控制[J]. 系统工程理论与实践,2013,33 (10) :2631–2638. CHEN Xiang-yong, JING Yuan-wei, LI Chun-ji. Optimal Control of Warfare Hybrid Dynamic System Based on Lanchester Equation[J]. Systems Engineering-Theory & Practice, 2013, 33 (10) : 2631–2638 . |
| [13] | 莫以为, 萧德云. 混合动态系统及其应用综述[J]. 控制理论与应用,2002,19 (1) :1–8. MO Yi-wei, XIAO De-yun. Overview of Hybrid Dynamic System and Its Application[J]. Control Theory and Applications, 2002, 19 (1) : 1–8 . |
| [14] | 杨莹, 陈国培, 李俊民. 随机混合动态系统的状态反馈控制[J]. 数学的实践与认识,2010,40 (14) :132–136. YANG Ying, CHEN Guo-pei, LI Jun-min. State Feedback Control of Stochastic Hybrid Systems[J]. Mathematics in Practice and Theory, 2010, 40 (14) : 132–136 . |
 2016, Vol. 33
2016, Vol. 33
