扩展功能
文章信息
- 王海波, 余志, 蔡铭
- WANG Hai-bo, YU Zhi, CAI Ming
- 不同顶端形态声屏障菲涅尔半波带衍射研究
- Study on Diffraction of Different Top Shaped Noise Barriers with Fresnel Half-wave Zone Method
- 公路交通科技, 2016, 33(5): 147-152,158
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 147-152,158
- 10.3969/j.issn.1002-0268.2016.05.023
-
文章历史
- 收稿日期:2014-09-09
2. 广东省智能交通系统重点实验室, 广东 广州 510006
2. Guangdong Provincial Key Laboratory of ITS, Guangzhou Guangdong 510006, China
近年来,道路交通环境问题日益严重,其中交通噪声问题因其严重影响人们日常生活和工作而广受关注。目前,对于交通噪声的防护,声屏障成为城区内公路铁路两侧普遍采用的降噪设施[1-2]。声屏障在噪声经过时对声音衍射衰减,从而降低声影区声场。对于不同顶端形态的声屏障,声音传播路径不同,声插入损失也不同。因此,研究不同顶端形态声屏障衍射规律,可为探究如何提高声屏障降噪效果提供依据。
国内外学者们已对声屏障进行了很多研究。目前研究方法方面主要有数值模拟[3-5]、缩尺模型[6]和实地测量[7-8]等方法。其中,因能快速模拟不同情况下声屏障声波衍射,声屏障数值模拟应用最为广泛[9]。在研究内容方面,已有的研究极为丰富。Chevret[10]对硬质声屏障对点声源的衍射衰减问题进行试验测量,试验结果反映了衍射衰减和波长、声屏障高度、衍射角的关系;郭萍[11]等考虑了侧边绕障的声压简化算法;Miki[12]研究了吸声材料对声屏障声学性能的影响。诸多研究中,声屏障顶端形状是极为重要的部分。张晓排[13]等通过缩尺模型试验研究了不同倾斜角度声屏障降噪效果;Shinichi[14]等通过在竖直屏障顶端加增简单几何结构来增加屏障隔声性能;陈永光[15]等应用计算机仿真技术对声屏障进行声学设计和衰减模拟。上述研究在特殊场景下对声屏障提出了改进,大多应用边界元或缩尺模型进行声屏障衰减模拟。
本文着力于研究不同顶端形态声屏障声插入损失规律。用菲涅尔半波带法[16],对竖直型、T型、Y型和折角型4种不同顶端形态的声屏障的插入损失进行计算。通过交通噪声算例,研究了4种屏障下插入损失垂直和水平变化规律。通过计算结果,对4种屏障的降噪效果做出了评价。
1 菲涅尔半波带衍射计算 1.1 声波方程的基本解点声源在三维全空间自由传播,声场方程可用极坐标形式表示:
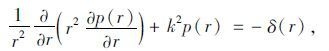
|
(1) |
式中,r为声源辐射半径;k为波数;p(r)为接收点声压级大小;δ(r)为声源特性。
不考虑遮挡情况下,声场中某点R的声压级p0(R)仅与该点到声源的距离d有关,其基本解为:
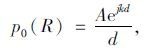
|
(2) |
式中,A为比例系数;j为虚数单位。
1.2 次级扰动带来的半波带声能贡献在遇到障碍物时,声波发生衍射现象。考虑到次级扰动带来的影响,本文对菲涅尔半波带的声能贡献进行计算。
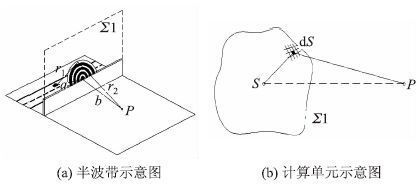
图 1为菲涅尔半波带衍射示意图。对于衍射所在立面的Σ1中任意微小单元dS,其对接收点R的影响满足方程:
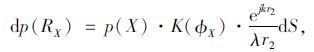
|
(3) |
式中,$p\left( X \right) = \frac{{A{e^{jk{r_1}}}}}{{{r_1}}}$,表示面元dS所在点X在自由场的基本解;K(φX)为倾斜因子。
接收点R第n阶半波带影响下声场为:
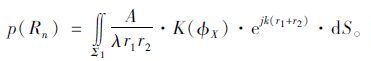
|
(4) |
对于任意阶数n的半波带,其长度满足:
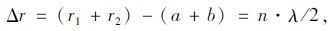
|
(5) |
式中,r1,r2分别为声源点和接收点到任意阶半波带的距离;a,b分别为声源点和接收点到屏障顶端的距离。
次级扰动下接收点的声场可表示为所有半波带影响的总和,即:
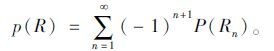
|
(6) |
对式(6)进行化简可得:
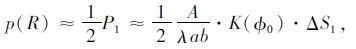
|
(7) |
式中,ΔS1为第一半波带面积;λ为波长。
|
| 图 1 菲涅尔半波带衍射图 Fig. 1 Noise diffraction of Fresnel half-wave zone |
| |
1.3 声屏障衍射计算
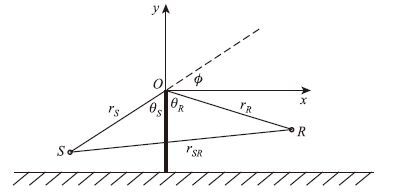
在实际声屏障场景下,如图 2所示。假设声源点S的坐标为(xS,yS,zS),接收点R的坐标为(xR,yR,zR),第一半波带面积可以表示为:
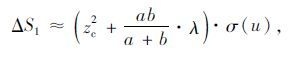
|
(8) |
式中,过渡函数σ(u)为随u增加而单调减小的递减函数;u和zc为过渡参数。各部分可通过式(9)~式(11)详细求解:
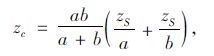
|
(9) |
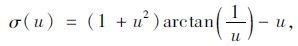
|
(10) |
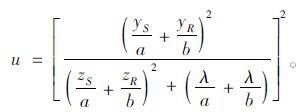
|
(11) |
衍射区域的声场p(R)可以用描述为:
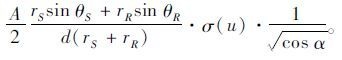
|
(12) |
式中,rS,rR分别为声源点和接收点到屏障顶端的距离;θS,θR为声源点到衍射点以及衍射点到接收点声音传播路径和声屏障的夹角。
声学中使用声插入损失来描述障碍物对声波的衰减影响,可由无障碍物的直达声与有屏障的绕射声的能量比值计算得到。文章方法下声屏障带来的插入损失可用表示为:
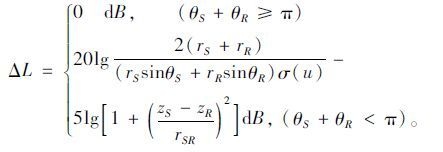
|
(13) |
|
| 图 2 声屏障噪声衍射衰减示意图 Fig. 2 Schematic diagram of noise barrier noise diffraction attenuation |
| |
2 声屏障交通噪声衍射衰减 2.1 不同顶端形态声屏障模型
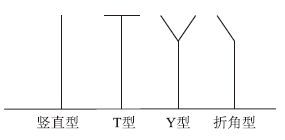
文章对竖直型、T型、Y型和折角型4种不同顶端形态的声屏障的声衍射衰减进行研究。4种类型的声屏障示意如图 3所示。
|
| 图 3 不同顶端形态声屏障 Fig. 3 Noise barriers with different top shapes |
| |
本文考虑次级扰动在声衍射中的作用,模型在三维空间中建立。在实际道路交通场景中,声屏障沿道路方向延伸长度远大于其高度和厚度尺寸,也远大于交通噪声(频率通常可视为500 Hz)的波长,并且道路交通噪声可以视为平行于声屏障的无限长线声源,故文章在道路交通噪声声场模拟中,将场景简化为垂直于道路平面的二维场景。
对于竖直型和折角型两种类型的声屏障,声音只在声屏障顶端发生一次衍射,相对于竖直型屏障,折角型屏障在计算过程中倾斜因子K(φX)不同,亦即通过式(13)在计算声屏障插入损失时,相关角度θS,θR以及长度参数不同。
对于T型和Y型两种类型的声屏障,空间区域可以划分成直达区、一次衍射区和双衍射区。在一次衍射区域,声衰减计算与上述3种类型屏障相同。当接收点位于双衍射区域时,其声屏障的插入损失可以表示为:
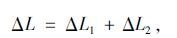
|
(14) |
式中,ΔL1为一次衍射带来的声音衰减;ΔL2为第二次衍射带来的声音衰减。
对于ΔL2,在计算过程中其积分面上各点X都在一次衍射区域内,所以可以取r1为从声源点绕过第一次衍射屏障到X的最短折线。其他计算与一次衍射相仿。
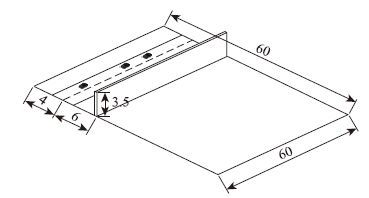
2.2 声屏障下交通噪声传播衰减模拟如图 4所示,本文设定了60 m×60 m的算例区域为研究对象,道路及声屏障位置如图所示。在计算中,选取与道路交通噪声最为相符的500 Hz声音。
|
| 图 4 交通噪声声屏障算例示意图(单位:m) Fig. 4 Schematic diagram of a computation case for traffic noise barrier(unit:m) |
| |
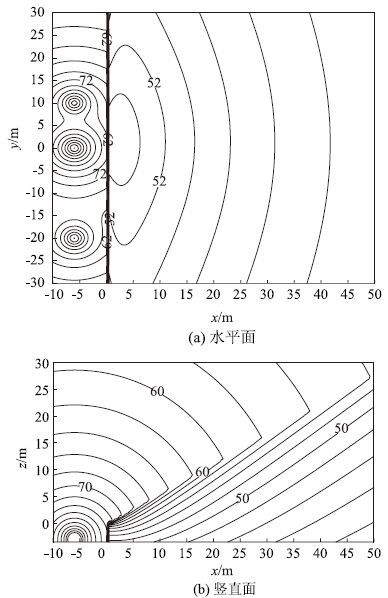
图 5为竖直型声屏障3 m高度水平面以及垂直于道路竖平面的声场分布图。从图中可以看出,菲涅尔半波带衍射计算能很好地模拟交通噪声在声屏障区域的衍射衰减。
|
| 图 5 声屏障区域交通噪声分布图(单位:dB) Fig. 5 Distribution of traffic noise in noise barrier area(unit:dB) |
| |
3 不同顶端形态声屏障降噪分析与讨论 3.1 声屏障插入损失
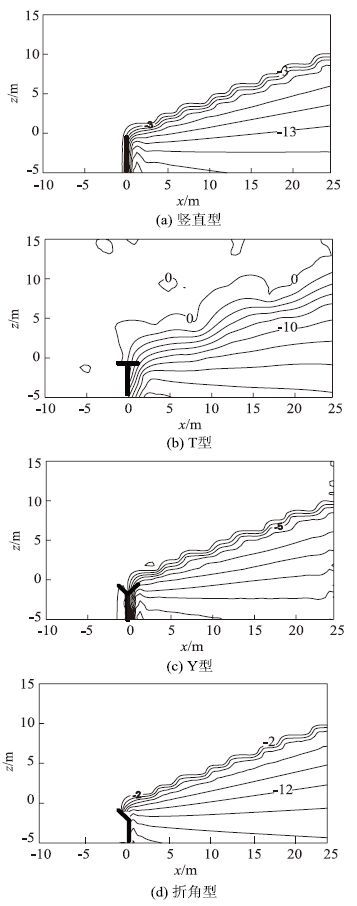
在不考虑声屏障长度影响,以及交通噪声源频率固定为500 Hz的前提下,本文从不同顶端形状方面出发分析声屏障的降噪效果。图 6为同一竖直参考面(y=0 m)下4种类型的声屏障的插入损失。
|
| 图 6 不同类型声屏障下噪声声场分布(单位:dB) Fig. 6 Distribution of noise field of different shaped noise barriers(unit:dB) |
| |
统计各种情况下计算区域内所有接收点的平均噪声值,不同顶端形态声屏障所呈现的声能插入损失,如表 1所示。
| 声压级 | 计算立面 | 衍射区域 | 最大值 |
| 竖直型 | 4.72 | 12.59 | 32.15 |
| T型 | 5.77 | 14.07 | 34.91 |
| Y型 | 5.37 | 14.21 | 33.27 |
| 折角型 | 5.09 | 13.54 | 33.12 |
从图 6及表 1中可以看出,4种结构声屏障对噪声均有明显的遮挡作用。其中T型和Y型声屏障对声音遮挡最为明显,其次为折角型屏障,在4种声屏障中,竖直型屏障的声插入损失最小。4种屏障下,对噪声遮挡最大的区域出现声影区最靠近屏障的区域,4种屏障的最大声插入损失均在33 dB左右。
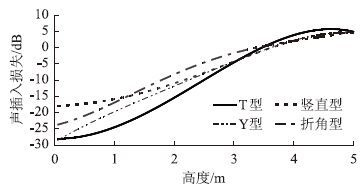
3.2 声插入损失垂直变化规律计算得到距声屏障5 m处声插入损失的垂直分布,如图 7所示。可以看出:在声影区(高度小于3.5 m),声屏障对声音衰减作用明显,最大衰减达到18~28 dB,4种屏障的声插入损失随高度增大而减少,其插入损失由大到小依次为T型、Y型、折角型和竖直型;在高度大于3.5 m时,声屏障的插入损失约等于0 dB,接收点声音可直达,声屏障对声场影响并不明显。
|
| 图 7 4种声屏障声插入损失垂直变化规律 Fig. 7 Vertical variation regularity of insertion loss of 4 shaped noise barriers |
| |
3.3 声插入损失水平变化规律
选取高度为1.5 m的水平面研究声屏障声插入损失的水平变化规律,4种屏障的插入损失如图 8所示。4种声屏障的声插入损失随着远离声屏障而减少,且趋势趋于平缓。对比4种声屏障结构,插入损失规律和垂直面相同,由大到小依次为T型、Y型、折角型和竖直型。
为避免真实道路场景中不同交通量、不同道路结构属性以及不同周边环境等对试验结果带来的不确定性,本文通过点声源试验的方式验证不同顶端形态声屏障的声音衰减特性。
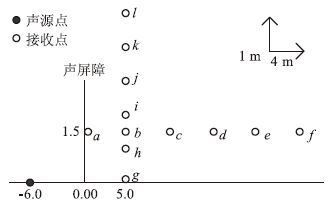
选取广州中山大学东校区罗马广场为试验场地,实测背景噪声为38 dB。发生器为单点定频率声源,选取与道路交通噪声最为相符的500 Hz声音作为测试声源,由发声装置发出,无声源指向性,在空旷空间7.5 m处测得声压级为84.5 dB,高度为0 m,距离声屏障6 m。声屏障由18 mm厚的实木胶合板组成,前后由5 mm厚高密集聚苯乙烯粘合,尺寸为10 m×3 m。测量时段平均风速为1.94 m/s,矢量变化小于1 m/s。本文选取了12个典型的声音接收点(编号为a-l)的声插入损失来评价不同顶端形态声屏障的降噪效果,接收点的位置如图 9所示。
|
| 图 9 声屏障测量试验点位选取(单位:m) Fig. 9 Selection of measuring points for testing noise barriers(unit:m) |
| |
4.2 试验结果分析
对于4种不同顶端形态的声屏障,分别测量其无声屏障时和加装声屏障时的声压级,并计算得到其在声音接收点所对应的声插入损失。测量结果如表 2所示。
| 测点 | 位置坐标/m | 插入损失/dB | ||||
| (距声屏障距离,高度) | 竖直型 | T型 | Y型 | 折角型 | ||
| a | 0,1.5 | 16.09 | 23.58 | 23.09 | 20.18 | |
| b | 5,1.5 | 14.65 | 21.68 | 19.24 | 17.65 | |
| c | 10,1.5 | 14.92 | 19.08 | 17.39 | 16.52 | |
| d | 15,1.5 | 13.98 | 18.24 | 17.23 | 16.09 | |
| e | 20,1.5 | 14.38 | 18.31 | 17.51 | 15.98 | |
| f | 25,1.5 | 14.64 | 18.34 | 17.34 | 16.34 | |
| g | 5,0 | 17.96 | 28.68 | 29.08 | 23.94 | |
| h | 5,1 | 15.84 | 25.31 | 21.64 | 17.92 | |
| i | 5,2 | 11.09 | 18.49 | 13.56 | 10.67 | |
| j | 5,3 | 8.06 | 7.56 | 7.49 | 7.31 | |
| k | 5,4 | 3.21 | 0.91 | 0.35 | 2.64 | |
| l | 5,5 | 0.29 | -0.68 | 0.47 | 1.27 | |
| 注: | ||||||
从表中可以看出,4种声屏障对声音有很大的遮挡作用,在声影区内,声屏障的插入损失表现为T型和Y型屏障最为明显。但当接收点到达一定高度以后,由于声波在声屏障边界区域的衍射作用,声音遮挡减弱,4种类型的声屏障遮挡效果趋于一致。
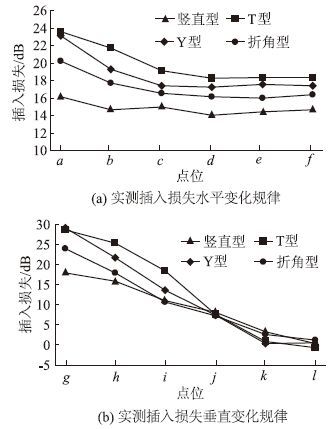
4种屏障的实测插入损失呈现的水平和竖直变化规律如图 10所示,可以看出其规律与上文相一致。声屏障的插入损失随着高度和离声屏障的距离的增加而减小,4种声屏障的降噪效果以此为T型、Y型、折角型和竖直型。
|
| 图 10 实测插入损失变化规律 Fig. 10 Variation regularity of measured insertion loss |
| |
综上所述,4种不同顶端形态声屏障表现出来的降噪效果不同。折角型声屏障面向声源弯折,相对于竖直型屏障,其形成的声影区的面积更大,对于靠近声屏障的声影区,其声音的路径也变大,故降噪效果比竖直型屏障好;而T型声屏障和Y型声屏障因为具有多重绕射边界,使得声音到达声影区的过程中必须经过2次明显衰减,造成其更明显的降噪效果。本文算例和实测场景下,大部分区域下T型屏障降噪效果略好于Y型屏障。
5 结论(1) 应用菲涅尔半波衍射研究声屏障的插入损失。文章算例下,4种屏障对噪声遮挡最大的区域出现声影区最靠近屏障的区域,声插入损失在33 dB左右。
(2) 算例和试验均表明,声屏障对声影区声场有明显的衍射作用,在声影区,声屏障的插入损失随着高度和离声屏障的距离的增加而减小。
(3) 文章所研究的4种结构声屏障对噪声均有明显的遮挡作用。声屏障几何形状对降噪效果的表现为T型和Y型对声音遮挡最为明显,其次为折角型屏障,竖直型屏障降噪效果最差。
| [1] | 蒋红梅, 张兰军. 国内外公路交通声屏障研究进展[J]. 公路交通技术,2007, (S1) :128–130. JIANG Hong-mei, ZHANG Lan-jun. Advances in Study on Acoustic Shielding in Expressway Traffic[J]. Technology of Highway and Transport, 2007, (S1) : 128–130 . |
| [2] | 洪宗辉, 潘仲麟. 环境噪声控制工程[J]. 北京:高等教育出版社,2002 . HONG Zong-hui, PAN Zhong-lin. Environmental Noise Control Engineering[J]. Beijing: Higher Education Press, 2002 . |
| [3] | LI K M, WONG H Y. A Review of Commonly used Analytical and Empirical Formulae for Predicting Sound Diffracted by a Thin Screen[J]. Applied Acoustics, 2005, 66 (1) : 45–76 . |
| [4] | 吴文高, 蔡俊, 刘玲. 顶端结构为声扩散体的声屏障降噪性能研究[J]. 噪声与振动控制,2012,32 (4) :121–125. WU Wen-gao, CAI Jun, LIU Ling. Study on Noise Reduction Performance of Sound Barrier with Acoustic Diffusers[J]. Noise and Vibration Control, 2012, 32 (4) : 121–125 . |
| [5] | OUIS D. Noise Attenuation by a Hard Wedge Shaped Barrier[J]. Journal of Sound and Vibration, 2003, 262 (2) : 347–364 . |
| [6] | 董华新, 刘岩, 杨冰, 等. 降噪声屏障及其缩尺模型试验方法研究[J]. 内燃机车,2011, (1) :18–20. DONG Hua-xin, LIU Yan, YANG Bing, et al. Noise Barrier and Its Scale Model Test Method[J]. Diesel Locomotives, 2011, (1) : 18–20 . |
| [7] | 王伟利. 公路交通噪声在声影区降噪量的计算探讨[J]. 环境科学与技术,2005,28 (1) :26–27. WANG Wei-li. Calculation of Road Traffic Noise Attenuation in Acoustic Shadow Zone[J]. Environmental Science and Technology, 2005, 28 (1) : 26–27 . |
| [8] | WATTS G R, GODFREY N S. Effects on Roadside Noise Levels of Sound Absorptive Materials in Noise Barriers[J]. Applied Acoustics, 1999, 58 (4) : 385–402 . |
| [9] | ISHIZUKA T, FUJIWARA K. Performance of Noise Barriers with Various Edge Shapes and Acoustical Conditions[J]. Applied Acoustics, 2004, 65 (2) : 125–141 . |
| [10] | CHEVRET P, CHATILLON J. Implementation of Diffraction in a Ray-tracing Model for the Prediction of Noise in Open-plan Offices[J]. The Journal of the Acoustical Society of America, 2012, 132 (5) : 3125–3137 . |
| [11] | 郭萍, 文桂林, 王艳广, 等. 三维有限长声屏障声压简化算法[J]. 公路交通科技,2012,29 (8) :153–158. GUO Ping, WEN Gui-lin, WANG Yan-guang, et al. A Simplified Method for Calculating Acoustic Pressure of 3D Finite Length Noise Barriers[J]. Journal of Highway and Transportation Research and Development, 2012, 29 (8) : 153–158 . |
| [12] | MIKI Y. Acoustical Properties of Porous Materials: Modification of Delany-Bazley Models[J]. Journal of the Acoustical Society of Japan, 1990, 11 (1) : 19–24 . |
| [13] | 张晓排, 刘岩, 钟志方. 不同倾斜角度声屏障降噪效果对比研究[J]. 噪声与振动控制,2009,29 (3) :73–74. ZHANG Xiao-pai, LIU Yan, ZHONG Zhi-fang. Comparison of Noise Reduction Effects for Different Inclinations of Sound Barrier[J]. Noise and Vibration Control, 2009, 29 (3) : 73–74 . |
| [14] | SHINICHI S, HIDEKI T. FDTD Analysis of Diffraction over Various Types of Noise Barriers[C]//Proceedings of 18 International Congress on Acoustics. Kyoto: Technical Acoustics,2004:252-254. |
| [15] | 陈永光, 袁启慧, 蔡伟明, 等. 声屏障声学设计与计算机仿真应用[J]. 噪声与振动控制,2013, (4) :182–184. CHEN Yong-guang, YUAN Qi-hui, CAI Wei-ming, et al. Acoustic Design of Sound Barriers and Simulation of Their Noise Control Performance[J]. Noise and Vibration Control, 2013, (4) : 182–184 . |
| [16] | 章力, 郑长聚. 用菲涅耳半波带法计算屏障的声插入损失[J]. 声学学报,1988,13 (5) :329–335. ZHANG Li, ZHENG Chang-ju. Calculating Sound Insertion Loss of a Barrier with Fresnel Zone Method[J]. Acta Acustica, 1988, 13 (5) : 329–335 . |
 2016, Vol. 33
2016, Vol. 33
