扩展功能
文章信息
- 刘志强, 刘恒, 汪澎, 倪捷, 周桂良
- LIU Zhi-qiang, LIU Heng, WANG Peng, NI Jie, ZHOU Gui-liang
- 基于不确定度理论的汽车与二轮车碰撞车速计算及验证方法研究
- Study on Calculation and Verification Methods of Collision Velocity between Vehicle and Two-wheelers Based on Uncertainty Theory
- 公路交通科技, 2016, 33(5): 135-140
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 135-140
- 10.3969/j.issn.1002-0268.2016.05.021
-
文章历史
- 收稿日期:2015-05-04
汽车与二轮车碰撞事故统计分析表明[1],转弯碰撞是二轮车事故中最普遍、最常见的碰撞类型,占总事故比例的一半以上。汽车行驶方向与二轮车运动方向之间的夹角绝对值在90°±20°范围内的二轮车事故占整个二轮车事故比例的70%,且碰撞位置大部分发生在汽车前部[2]。这类事故有一个共同点:碰撞后二轮车或者骑乘人员很容易被抛出,且人员的伤亡率很高。
碰撞车速是交通事故鉴定和责任认定过程中的重要依据。然而,在实际交通事故案例现场勘查过程中,现场采集的许多参数不是唯一的准确值,碰撞瞬时速度的取值一般依经验判定,这导致了事故责任认定的不可靠性[3]。本文引入不确定度评定方法、数值校验及软件模拟仿真的验证方法,以期提高碰撞车速计算精度和事故再现结果的可靠性。
1 不确定度理论 1.1 多元函数的相对不确定度评定不确定度理论可对理论真实值进行估算,并相应地给出一个用于表示被测量结果不确定性的合理取值范围[4]。对于多元函数y=f(x1,x2,x3,…,xn),y受到若干个具有不确定因素输入量xi(i=1,2,…,n)的影响,即目标函数y的相对标准不确定度分量u′yi取决于每个不相关输入量xi的相对标准不确定度u′xi。相对合成标准不确定度u′y扩展后,可得到最佳函数目标y的取值范围[5],评定流程如图 1所示。

|
| 图 1 不确定度评定方法流程图 Fig. 1 Flowchart of uncertainty evaluation method |
| |
1.2 不确定度方法在事故车速鉴定中的应用
在汽车与二轮车碰撞事故鉴定中,事故车速计算流程如图 2所示。基本流程:数据采集→建立碰撞过程模型→车速计算及不确定度评定→数值校核及模拟仿真验证。在此过程中,不确定度理论应用于建模前的参数输入过程以及建模后结果部分的精度分析[6],以此提高参数的准确性和结果的可靠性。

|
| 图 2 事故车速计算流程图 Fig. 2 Flowchart of calculation of accident speed |
| |
2 骑车人和二轮车抛距-碰撞车速模型
轿车与二轮车发生碰撞时,一般骑车人的重心高度高于轿车前端,则碰撞后的人体运动可分为加载行驶、空中飞行和地面运动3个阶段。由于碰撞接触时间非常短,可视为在瞬间完成,即人体或二轮车的水平输送距离可以忽略,则二轮车骑乘人员抛距由空中自由飞行距离Lf和地面滑移距离Ls两部分组成,汽车与二轮车碰撞过程及最终停止位置如图 3所示[7]。

|
| 图 3 人体、二轮车抛距-碰撞车速模型 Fig. 3 Throwing distance vs. collision speed model of human and two-wheeler |
| |
二轮车或乘员的质量与汽车质量相差悬殊,且以小角度碰撞时,二轮车质量在汽车运动方向上的分量较小,因此,可以忽略汽车与二轮车碰撞时人、二轮车系统对汽车速度的影响。由于两者之间的碰撞不是完全非弹性碰撞,因此,设骑乘人抛出速度Vp是汽车碰撞速度V的k倍,k也称为抛射系数或碰撞因子[9],即:
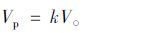
|
(1) |
在自由飞行阶段,设骑乘人员被抛出时的等效质心高度为hp,抛射角度为θp,骑乘人员在空中的飞行时间为tf,则骑乘人员在空中抛出直至第1次落点之间的水平距离Lf为:

|
(2) |
式中,Vpfy为骑乘人员落地瞬间速度在垂直方向上的分量;g为重力加速度,取值9.8 m/s2。
由动能定理可得骑乘人员落地瞬间的垂直速度Vpfy为:
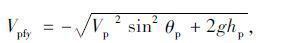
|
(3) |
骑乘人员落地瞬间的水平速度Vpfx为:

|
(4) |
在地面滑行距离Ls落地后,骑乘人员在垂直方向的速度V′pfy近似为0,即V′pfy=0。设路面对人体向上的作用力为F,作用时间为t,同时考虑到垂直冲量对水平速度的影响,假设骑乘人员的质量为mp,人体初始滑移速度为V′pfx,人体在地面滑动的摩擦系数为μp,则在平行和垂直路面的方向上,根据冲量定理得:

|
(5) |
最终静止时,人体速度Vps=0,滑移距离Ls为:

|
(6) |
综合式(1)~(6),可得骑乘人员抛距L与碰撞车速V的关系为:

|
(7) |
变换式(7),将其表示为V=f(L)的形式[10]:
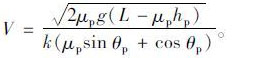
|
(8) |
同理,二轮车抛距-碰撞车速模型的推导与骑乘人员-车速碰撞模型推导过程相同,可得二轮车抛距L与碰撞车速V′的关系为:
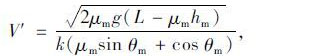
|
(9) |
式中,θm为二轮车被撞后抛射角;μm为二轮车在地面上滑动的摩擦系数;hm为二轮车被抛出时等效质心高度。
3 案例分析某轿车沿104国道由东向西行驶,行至104国道1 165.2 km处附近时,与沿乡村道路由南向北驶入104国道实施左转弯的某电动自行车发生碰撞,事故后轿车向西偏北方向滑行15.5 m后停下;骑车人被撞到离撞击点前方17.5 m处,电动自行车则停在距撞击点以西约25 m处。该轿车的整备质量为1 275 kg,总质量为1 785 kg,外廓尺寸为4 454 mm×1 765 mm×1 460 mm,电动车质量为40 kg,外廓尺寸为1 800 mm×660 mm×1 090 mm。
3.1 碰撞过程建模及车速计算在上述案例中,现场采集的数据资料包括准确参数、测量数据和经验参数。由于测量数据的近似性和经验参数的不确定性,因此车速计算过程引入了不确定性。根据骑乘人员及电动自行车抛距,建立了骑乘人员抛距模型和电动自行车抛距模型。
3.1.1 由骑乘人员抛距模型获取等效车速骑乘人员在碰撞发生后被抛出距离L约为17.5 m,被抛出时的等效质心高度hp近似为0.8 m,以骑乘人员与地面间的滑动摩擦系数μp和抛射角度θp为不确定因子[11],μp=0.64~0.7,即μp=0.67±0.03。根据I.Han和R. M. Brach进行的相关试验研究[12],对于汽车与电动车(摩托车)或骑乘人员之间的抛射系数k以及抛射角度θ的推荐取值为:对于斜抛运动,k=1.0,θ∈[5°,10°];对于平抛运动,k=1.0,θ=0°。因此,此案例中针对人体抛距建立的模型抛射系数k=1.0,抛射角度θp=5°~10°,即θp=7.5°±2.5°。根据式(8)计算出等效碰撞车速: V1=13.83 m/s=49.80 km/h。
3.1.2 由电动自行车抛距模型获取等效车速碰撞发生后,电动自行车抛出距离L约为25 m,以电动自行车在地面上滑动的摩擦系数μm和发生碰撞时的等效质心高度hm为不确定因子,即μm=0.55~0.7=0.625±0.075,hm=0.3H~0.4H=0.38±0.055 m (H为车体高度)。在汽车与二轮车碰撞事故中,绝大部分二轮车的抛出形式为平抛运动,故抛射系数k=1.2,抛射角度θm=0°。同理,根据式(9)计算出等效碰撞车速: V2=14.51 m/s=52.25 km/h。
3.2 不确定度评定(1) 根据骑乘人员抛距模型计算碰撞车速时,可知影响车速的不确定因子包括滑动摩擦系数μp和抛射角度θp,两个参数的偏导数形式为:
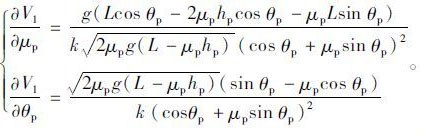
|
(10) |
针对骑乘人员抛距模型中的不确定因子μp和θp进行不确定度理论评定,其结果如表 1所示。估算车速的相对合成标准不确定度u′(V1)=1.41%,可得相对扩展不确定度为: U′=2×1.41%=2.82%。
因此,碰撞车速V1的取值范围为: V1=(13.83±13.83×2.82%)m/s= 48.40~51.2 km/h。
(2) 根据电动自行车抛距模型计算碰撞车速时,可知影响车速的不确定因子包括滑动摩擦系数μm和等效质心高度hm,两个参数的偏导数形式为:
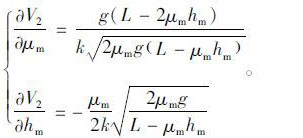
|
(11) |
针对电动自行车抛距模型中的不确定因子μm和hm进行不确定度理论评定,其结果如表 2所示。估算车速的相对合成标准不确定度u′(V2)=2.97%,可得相对扩展不确定度为: U′=2×2.97%=5.94%。
因此,碰撞车速V2的取值范围为: V2=(14.51±14.51×5.94%)m/s= 49.15~55.35 km/h。
| 输入分量 xi | xi变化半范 围ai | 包含因子 ki | 标准不确 定度u(xi) | 相对标准不确定度u′(xi) |
不确定度传递系数 | 相对标准不确定度分量u′(Vi) |
| μm | 0.075 | 2 | 0.037 5 | 0.06 | 11.50 | 0.029 7 |
| hm | 0.055 | 2 | 0.027 5 | 0.072 4 | 0.183 2 | 0.000 3 |
| 相对合成标准不确定度u′(V2) | 0.029 7 | |||||
综合比较骑乘人员抛距模型和电动自行车抛距模型的评定结果与涉及的相关不确定性因子,对于95%的置信概率[14],骑乘人员抛距模型的相对扩展不确定度未超过5%,而电动自行车抛距模型的相对扩展不确定度超过5%,并且前者所得的瞬时碰撞车速几乎是后者瞬时碰撞车速的一个子区间,可以有效地控制结果的误差度,故针对此案例骑乘人员抛距建模所得的车速作为最终理论计算的结论比较合适。
4 验证 4.1 数值校核利用MATLAB中的Meshgrid函数[15]对骑乘人员抛距模型所涉及的参数及所得结果进行数值校核。在不确定因子μp和θp的影响下,碰撞车速V的取值变化情况如图 4所示。其中最大车速为51.91 km/h,最小车速为47.95 km/h,平均值为49.93 km/h。与不确定度评定结果比较,不确定度评定的车速最佳取值范围全部落在MATLAB校核的车速三维变化区间内,不确定度评定的车速平均值与数值校核的平均值相比误差度为0.27%。因此不确定度理论的评定方法在事故车速鉴定中可以有效地控制计算精度。
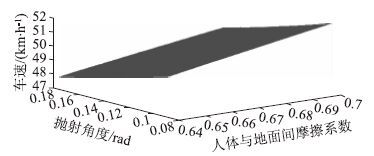
|
| 图 4 车速三维变化区间图 Fig. 4 Three-dimensional graph of speed range |
| |
4.2 仿真验证
使用PC-Crash[16]模拟整个碰撞事故过程,并针对骑乘人员抛距模型的车速计算,并对不确定度评定结果进行仿真和对比验证。将在事故现场采集到的车辆、骑乘人员及电动自行车的数据输入到PC-Crash模型中,设轿车以-2.28°的车偏角与20 km/h的速度[17]与骑乘朝向为-83.2°的电动自行车在国道交叉口发生碰撞,经0.8 s的反应时间后,轿车采取紧急制动,其减速度约为6.17 m/s2。假设仿真过程中,保持其他设置参数不变,以轿车、骑乘人员及电动自行车的最终落点位置为目标函数,以碰撞车速为自变量进行模拟优化。当在PC-Crash中设置汽车碰撞瞬时速度为47~53 km/h时,碰撞后的车辆滑行距离、骑乘人及电动自行车的抛距比较接近实际案例,如表 3所示。
| 试验号 | 碰撞前车速/ (km·h-1) | 碰撞后轿车 滑行距离/m | 骑车人 抛距/m | 电动自行车抛距/m |
| 1 | 47 | 12.9 | 15.4 | 19.6 |
| 2 | 48 | 12.9 | 15.6 | 21.1 |
| 3 | 49 | 13.8 | 16.9 | 22.6 |
| 4 | 50 | 14.2 | 16.7 | 25.3 |
| 5 | 51 | 14.7 | 17.4 | 24.8 |
| 6 | 52 | 14.9 | 17.2 | 25.7 |
| 7 | 53 | 15.2 | 17.7 | 26.2 |
根据模拟仿真结果可知,轿车碰撞前的瞬时车速为V=51 km/h时,最接近上述碰撞中轿车、骑车人及电动自行车的最终停止位置,如图 5所示。在3D仿真视图中,骑车人的头部与轿车前挡风玻璃左前下方进行第1次接触,与实际挡风玻璃凹陷裂纹情况吻合。模拟仿真的结果证明了骑乘人员抛距-碰撞车速模型和不确定度评定的结果是有效的。
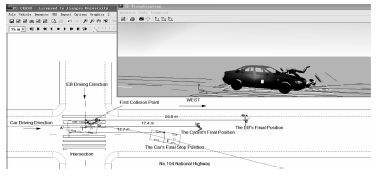
|
| 图 5 PC-Crash仿真界面 Fig. 5 PC-Crash simulation interface |
| |
4.3 行驶记录仪分析
因为轿车装有GPS视频行驶记录仪(Video Drive Recorder,VDR),可以有效地记录碰撞发生前20 s内的车辆速度变化情况和驾驶员采取的措施情况[18]。根据VDR的历史数据记录可知,在碰撞发生前一刻,驾驶员已采取了紧急制动,使车速急剧下降到40 km/h以下,经2 s后汽车停止滑行。因此,通过VDR获取的碰撞时刻车速变化信息也间接证明了骑乘人员抛距模型和不确定度评定的可靠性。
5 结论(1) 针对一起轿车与电动行车碰撞事故案例,建立了骑乘人员和电动自行车抛距-碰撞车速模型,运用不确定度评定方法,提高了事故鉴定中车速计算的精度。
(2) 通过MATLAB数值校核、PC-Crash模拟仿真和行驶记录仪分析验证,证明了模型和不确定度评定理论的有效性和可靠性。
| [1] | 公安部交通管理局. 中华人民共和国道路交通事故统计年报(2013年度). 无锡:公安部交通管理研究所[M]. 2013 . Traffic Management Bureau of Ministry of Public Security. Road Traffic Accident Statistics Annual Report (2013) of the People's Republic of China. Wuxi: Traffic Management Institute of Ministry of Public Security[M]. 2013 . |
| [2] | 袁泉, 李一兵, 郭榕. 用于统计与分析的汽车碰撞行人事故深入数据源[J]. 公路交通科技,2008,25 (5) :121–129. YUAN Quan, LI Yi-bing, GUO Rong. In-depth Data Source of Vehicle-to-pedestrian Accidents Used in the Statistic and Analysis of Accidents[J]. Journal of Highway and Transportation Research and Development, 2008, 25 (5) : 121–129 . |
| [3] | 刘志强, 汪澎, 张建华. 交通事故再现技术研究现状与发展趋势[J]. 中国安全科学学报,2007,17 (4) :16–20. LIU Zhi-qiang, WANG Peng, ZHANG Jian-hua. Review of Traffic Accident Reproduction Technology and Its Developing Trend[J]. China Safety Science Journal, 2007, 17 (4) : 16–20 . |
| [4] | 费业泰. 误差理论与数据处理. 北京:机械工业出版社[M]. 2010 . FEI Ye-tai. Error Theory and Data Processing. Beijing: China Machine Press[M]. 2010 . |
| [5] | 李一兵, 袁泉, 陈理. 车辆碰撞行人交通事故事故的不确定因素研究[J]. 中国公路学报,2004,17 (1) :82–85. LI Yi-bing, YUAN Quan, CHEN Li. Study of Uncertain Factors in Traffic Accidents of Vehicle Impacting Pedestrian[J]. China Journal of Highway and Transport, 2004, 17 (1) : 82–85 . |
| [6] | 袁泉, 张高强, 李一兵, 等. 交通事故车速分析理论方法的研究进展[J]. 交通运输工程与信息,2009,7 (2) :21–27. YUAN Quan, ZHANG Gao-qiang, LI Yi-bing, et al. Research Evolution on the Theory Methods of Vehicle-speed Analysis of Traffic Accidents[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 7 (2) : 21–27 . |
| [7] | 林庆峰, 许洪国, 成波. 交通事故行人,骑车人和自行车抛距模型[J]. 交通运输系统工程与信息,2006,6 (6) :73–78. LIN Qing-feng, XU Hong-guo, CHENG Bo. Throw Model of Pedestrian,Bicyclist and Bicycle in Traffic Accident[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6 (6) : 73–78 . |
| [8] | 许骏, 李一兵. 人车碰撞事故再现技术综述[J]. 汽车工程,2009,31 (11) :1029–1033. XU Jun, LI Yi-bing. An Overview on the Technique of Accident Reconstruction for Pedestrian-vehicle Crash[J]. Automotive Engineering, 2009, 31 (11) : 1029–1033 . |
| [9] | TOOR A. Theoretical Versus Empirical Solutions for Vehicle/Pedestrian Collisions[C]//Crash Reconstruction Research: 20 Years of Progress (1988-2007). Warrendale, PA: SAE, 2008. |
| [10] | DEPRIESTER J P, PERRIN C, SERRE T, et al. Comparison of Several Methods for Real Pedestrian Accident Reconstruction[C]//Proceedings of 19th International Technical Conference on the Enhanced Safety of Vehicle. Washington, D.C.: National Highway Traffic Safety Administration, 2005:05-0333. |
| [11] | 袁泉, 李一兵, 裴剑平. 交通事故车速估算的不确定因子方法[J]. 交通运输工程学报,2001,1 (4) :71–74. YUAN Quan, LI Yi-bing, PEI Jian-ping. The Uncertain Factor Method for Vehicle-velocity Estimate in Traffic Accident[J]. Journal of Traffic and Transportation Engineering, 2001, 1 (4) : 71–74 . |
| [12] | HAN I, BRACH R M. Impact Throw Model for Vehicle-Pedestrian Collision Reconstruction[J]. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, 2002, 216 (6) : 443–453 . |
| [13] | 薛大伟, 白竹, 孙云霞. 基于不确定度评定的交通事故车速估计方法[J]. 黑龙江工程学院学报,2009,23 (4) :36–40. XUE Da-wei, BAI Zu, SUN Yun-xia. Evaluation Method of Traffic Accident Velocity Based on Uncertainty[J]. Journal of Heilongjiang Institute of Technology, 2009, 23 (4) : 36–40 . |
| [14] | 上海市计量测试技术研究院. 常用测量不确定度评定方法及应用实例. 北京:中国计量出版社[M]. 2001 . Shanghai Institute of Measurement and Testing Technology. Uncertainty Evaluation Methods and Application Examples of Commonly Used Measurement. Beijing: China Measurement Press[M]. 2001 . |
| [15] | ATTAWAY S. MATLAB: A Practical Introduction to Programming and Problem Solving. 3rd ed. Boston: Elsevier[M]. 2013 . |
| [16] | 金先龙, 张晓云. 交通事故数字化重构理论与实践. 北京:人民交通出版社[M]. 2007 . JIN Xian-long, ZHANG Xiao-yun. Theory and Practice of Digital Reconstruction of Traffic Accident. Beijing: China Communications Press[M]. 2007 . |
| [17] | 徐雪梦, 林庆峰, 王伟. 轿车-电动自行车侧面碰撞事故再现分析[J]. 长安大学学报:自然版,2013,33 (1) :85–88. XU Xue-meng, LIN Qing-feng, WANG Wei. Reconstruc-tion Analysis of Car-electric Bicycle Side Impact Accident Based on Pc-Crash[J]. Journal of Chang'an University: Natural Science Edition, 2013, 33 (1) : 85–88 . |
| [18] | 赖俊科, 成波, 林庆峰, 等. 图像式汽车行驶记录仪在交通冲突成因分析中的应用[J]. 中国农业大学学报,2008,13 (5) :97–102. LAI Jun-ke, CHENG Bo, LIN Qing-feng, et al. Application of Video Drive Recorder in the Cause Analysis of Traffic Conflicts[J]. Journal of China Agricultural University, 2008, 13 (5) : 97–102 . |
 2016, Vol. 33
2016, Vol. 33
