扩展功能
文章信息
- 龙雪琴, 宋嘉骐, 王建军, 关宏志
- LONG Xue-qin, SONG Jia-qi, WANG Jian-jun, GUAN Hong-zhi
- 面向有限理性决策的出行者行为研究
- Study on Traveler's Behavior for Bounded-rational Decision-making
- 公路交通科技, 2016, 33(5): 105-110
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 105-110
- 10.3969/j.issn.1002-0268.2016.5.017
-
文章历史
- 收稿日期:2015-03-30
2. 北京工业大学 交通工程北京市重点实验室,北京 100124
2. Beijing Key Lab of Traffic Engineering,Beijing University of Technology,Beijing 100124,China
近年来,随着社会经济的发展,交通流量增大,突发交通事故时有发生,严重影响路网的整体效率。因此研究突发交通事故下出行者的路径选择行为,对于制订交通诱导方案非常必要。
传统的路径选择行为理论是在期望效用理论的框架下进行的。但是研究发现,即使在最理想的环境下,决策者的行为也会表现出明显的背离期望效用理论的现象。
经济学家Simon最早提出了有限理性的概念[1],1979年Kahneman和Tversky在有限理性的基础上提出了前景理论,又提出了修正版的累积前景理论[2]。此后,大批学者[3-7]采用前景理论对出行者路径选择进行建模,分析了前景理论和期望效用理论在描述出行行为方面的差异性。
Connors[4]、张波[5]、徐红利等[6]基于累积前景理论建立了固定需求条件下的用户平衡模型,对路网均衡配流进行了研究。刘玉印[7]以累积前景理论为基础,建立了出行者感知效用模型,对比分析了分别应用期望效用理论和累积前景理论时,出行者路径选择行为的差异。Wang[8]、Song等[9]研究了出行者在面对风险情况下的逐日路径选择行为,并对比试验结果,发现累计前景理论比期望效用理论更符合出行者实际出行行为。夏金娇[10]在前景理论框架下,研究了通勤出行者路径选择模型中参考点的设置,探究了出发时刻对通勤者路径选择的影响。胡晓伟[11]将前景理论引入方式选择决策中,分析了有限理性下出行者的方式选择行为,对比分析结果与期望效用理论,发现前景理论更依赖于决策权重函数的变化。
以上研究说明,出行者行为选择中存在有限理性,且有限理性更符合出行者真实的出行行为。目前出行者有限理性研究已较成熟,完全可以应用于出行行为分析。
但是,目前在突发交通事故后出行者的行为研究中,并没有考虑出行者的有限理性。 Erke[12]、Guattari[13]研究了VMS的位置、提示信息与出行行为的关系,结果显示约1/5的车根据提示信息改变了原有路径。Ma等[14]设计了调查问卷,建立了多项logit模型,分析了出行者个人和家庭、社会属性等因素与出行行为之间的关系。以上研究更多关注了VMS信息发布对路径选择的影响,忽略了事故本身特征的影响,没有更深层次地揭露事故与出行行为之间的相互影响关系。
本文以有限理性理论为基础,建立出行效用连续随机分布的路径选择模型,揭示不同事故持续时间下出行者的有限理性决策过程,进一步研究出行行为选择规律。
1 路径动态决策 1.1 场景假设路网中存在多条路径,路径j的正常出行时间tj服从正态分布tj~N(μj,σj2),μj和σj分别为路径j正常出行时间的均值和标准差。路径j的正常通行能力为cj。假设路径1的正常通行能力为c1,路径1上突发交通事故,通行能力降为c,事故消散时间r服从正态分布r~N(μ0,σ02),μ0和σ0分别为事故路径(路径1)事故消散时间的均值和标准差。事故上游交叉口处设置有可变信息版VMS,VMS与事故点之间的间距为L1,事故点到下一出口的距离为L2。事故T1小时后被发现,VMS第1次告知出行者交通事故信息,根据初始交通流率预测并发布交通消散时间r(即道路上排队长度为0,交通恢复正常的时间)的均值为μ0,1;此后,每隔Δt的时间间隔,VMS根据上次出行者的选择结果持续更新时间信息,第k次发布事故消散时间的均值为μ0,k,出行者始终根据上次信息发布的时间进行路径选择,并作为下一时间间隔计算事故持续时间的依据。
事故发生前,道路上的车头间距为hd。假设救援车辆在T1时刻到达VMS处,0-T1时间范围内,交通流仍按照原来的流率进入,救援车辆从VMS处到达事故点所需时间T2为:
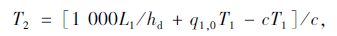
|
(1) |
式中q1,0为事故路径1的初始交通流率。
设事故处理时间为T3(它与事故的类型和严重程度有关),则事故持续时间d为:
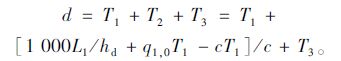
|
(2) |
美国FHWA《交通控制系统手册》中给出了不同类型紧急事件下的道路有效通行能力系数,具体见文献[15]。
1.2 动态决策过程对于事故路径,k=1时,VMS第1次发布事故消散时间r0,1的均值μ0,1。排队长度Q0,1为:
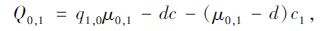
|
(3) |
则第1次发布事故消散时间的均值μ0,1为:
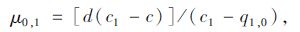
|
(4) |
此时,路径1的正常出行时间t1,1的均值为:
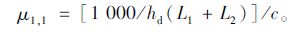
|
(5) |
k>1时,第k次发布事故消散时间的均值μ0,k为:
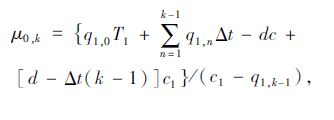
|
(6) |
式中,q1,n为第n个时间间隔进入事故路径1的流量;q1,k-1同理。
当(k-1)Δt≤d时,路径1的正常出行时间t1,k的均值μ1,k为:
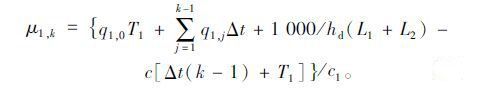
|
(7) |
当(k-1)Δt>d时,说明事故已被清理,通行能力恢复,路径1的正常出行时间均值μ1,k为:
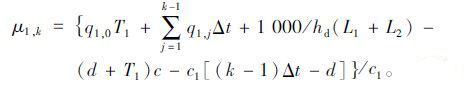
|
(8) |
对于其他路径j(j≠1),出行时间的均值μj,k为:
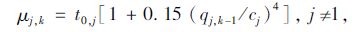
|
(9) |
式中,t0,j为路径j(j≠1)的自由流出行时间;qj,k-1为在上一时间间隔k-1时进入路径j的流量。
根据概率论统计知识,正态分布密度函数中的方差可近似取均值和最小值之差的1/3[16],则第k个时间间隔,路径j出行时间的方差σj,k、事故路径(路径1)出行时间的方差σ0,k分别为:
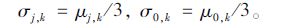
|
(10) |
每隔Δt时间,出行者根据上次信息发布的内容,更新所有路径的出行时间均值μj,k和事故消散时间均值μ0,k。然后,出行者按前情景理论,判断各条路径的“收益”与“损失”,选择具有最大前景值的路径出行,路径选择结果qj,k作为下次信息发布的依据。
2 前景理论前景理论放弃了原有的效用最大化理论,基于有限理论的基础,认为个体在面临收益时会规避风险,面临损失时会追求风险,且个体对风险的敏感性大于对收益的敏感性,是有限理性理论的代表理论。
2.1 效用函数设路径的效用为x,参考点为x0,出行者的主观效用可以分为收益(x≥x0)和损(x≤x0),失Tversky等[17]提出的主观效用函数v(x)为:
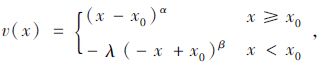
|
(11) |
式中,α,β,λ均为参数。α,β取值为0~1之间,其值越大表明决策者越倾向于冒险。λ取值大于1,表明决策者对损失的敏感性较大。
当发生交通事故并导致交通拥挤后,交通流将形成排队现象。设t0为期望出行时间,t1为事故路径正常出行时间,tj(j≠1)为其他路径正常出行时间,r为事故消散时间,认为只要总的出行时间大于期望出行时间,路径的效用为负,出行者面临损失;反之,路径的效用为正,出行者面临收益,即参考点x0=0。u0和uj分别为事故路径和其他路径j出行时间的均值,σ0和σj分别为事故路径和其他路径j出行时间的方差。以下分别讨论事故路径和正常路径(未发生交通事故的路径)的出行效用。
(1) 对于事故路径
选择路径1,出行者的盈余(超过)时间为T=t0-t1-r。假设路径的效用为盈余(超过)时间的eT,那么:
① 出行者面临收益(t0≥t1+r)时,效用为:
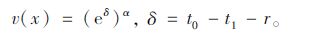
|
(12) |
出行者效用v(x)服从参数为α(-μ0+t0-μ1)和(ασ0σ1)2的对数正态分布。
② 面临损失(t0≤t1+r)时,效用为:
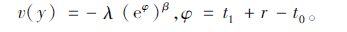
|
(13) |
出行者效用v(y)服从参数为β(μ0-t0+μ1)+ln λ和(βσ0σ1)2的对数正态分布。
(2) 对于正常路径
正常路径不存在事故消散时间,因此选择路径j,出行者的盈余(超过)时间T=t0-tj,假设路径的效用为盈余(超过)时间的eT,那么:
① 出行者面临收益(t0>tj)时,效用为:
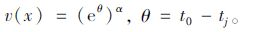
|
(14) |
出行者效用v(x)服从参数为α(t0-μj)和(ασj)2的对数正态分布。
② 面临损失(t0<|<tj)时,效用为:
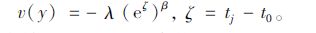
|
(15) |
出行者效用v(y)服从参数为(-t0+μj)β+ln λ和(βσj)2的对数正态分布。
2.2 主观概率函数Tversky 等提出了主观概率函数的形式[18]:
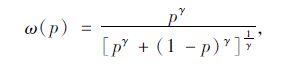
|
(16) |
式中,p为选择概率;ω(p)为主观概率函数;γ为参数。Kahneman经过试验标定,在面临收益时,γ=0.61;面临损失时,γ=0.69。
2.3 备选路径的前景值设一条路径的效用是有限离散的,将效用x按从小到大的顺序进行排列,xi=(x-m,x-m+1,…,xn-1,xn),对应的选择概率为pi=(p-m,p-m+1,…,pn-1,pn),该条路径感知效用(即前景值)为:v=v++v-。且有[7]:
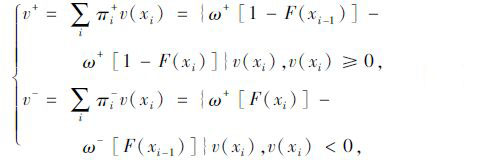
|
(17) |
式中, v+,v-分别为出行者感知效用的收益和损失;π+i,π-i分别为感知效用的收益和损失概率;ω+(),ω-()分别为收益、损失的概率权重函数;F(xi)为路径效用xi的累积概率函数,F(xi-1)同理。
2.4 连续函数离散化根据上述分析可得,出行者感知效用服从对数正态分布。本文采用连续函数离散化的方法,以Δx为间隔,将出行者感知效用划分为若干个小区间,计算任意第i个小区间的出行者效用xi。
假设以99.8%的置信度来判断事故持续时间r和路径j出行时间tj的分布范围,可认为事故延误时间的最大值max r=u0+3.09σ0,最小值min r=max(0,u0-3.09σ0);路径j的出行时间最大值maxtj=uj+3.09σj,出行时间最小值mintj=max(0,uj-3.09σj)。
(1) 对于事故路径
面临收益时,收益x的最大值xn、最小值x1分别为:
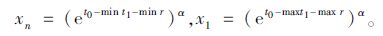
|
(18) |
第i个收益中间值xi为:
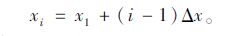
|
(19) |
xi的概率密度函数为:
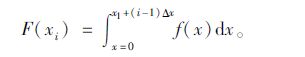
|
(20) |
面临损失时,损失y的最大值x-1、最小值x-m分别为:
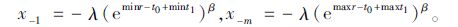
|
(21) |
第i个损失中间值xi为:
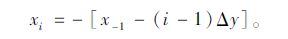
|
(22) |
xi的概率密度函数为:
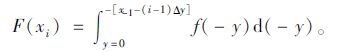
|
(23) |
(2) 对于正常路径
面临收益时,收益x的最大值xn、最小值x1分别为:
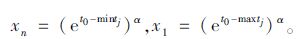
|
(24) |
第i个收益中间值xi为:
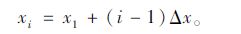
|
(25) |
xi的概率密度函数为:
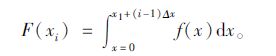
|
(26) |
面临损失时,损失y的最大值x-1、最小值x-m分别为:
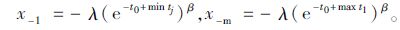
|
(27) |
第i个损失中间值xi为:

|
(28) |
xi的概率密度函数为:
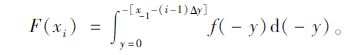
|
(29) |
在每个时间间隔k,出行者比较两条路径的前景值,并最终选择前景值较大的路径,得到每条路径的流量qj,k。VMS据此发布下一时间间隔的事故消散时间,并作为出行者选择依据,直至最终事故完全消散。
3 算例如图 1所示,路径1上发生了一起交通事故。
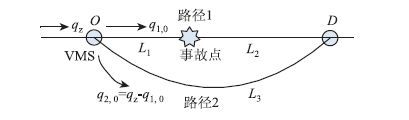
|
| 图 1 场景假设 Fig. 1 Scene hypothesis |
| |
(1) 仿真试验
参数取值如下表 1所示。
| T1/h | T3/h | c1/(pcu·h-1) | c2/(pcu·h-1) | c/(pcu·h-1) | Δt/h | L1/km | L2/km | L3/km | hd/m | t0,1/h | t0,2/h |
| 0.1 | 0.2 | 3 000 | 2 500 | 1 225 | 0.1 | 1.5 | 2 | 4 | 40 | 0.15 | 0.30 |
进入节点O的交通总量qz=4 000 pcu/h,事故发生前每条路径的流量分别为q1,0=2 500 pcu/h,q2,0=1 500 pcu/h。假设每个出行者对收益和损失的敏感性不同,α和β在0~1之间随机取值,λ在1~5之间随机取值。
① t0=0.4 h。当k=1时,由于路径1(事故路径)延误时间长,其前景值远远小于路径2,因此所有出行者均选择路径2出行;当k=2时,上一阶段路径2的流量为4 000 pcu/h,道路异常拥堵,前景值下降,而路径1上未出现出行者,其前景值增加,对部分出行者而言,路径1的前景值比路径2大,因此路径1上出现出行者。此后,这种此消彼长的现象一直持续,且随着事故的逐渐消散,两条路径之间的流量差逐渐减小,直至k=8(48 min),事故完全消散。此时,路径1的流量大于路径2,因为路径1的通行能力较路径2大。
当k>9时,各条路径的流量基本保持不变,由于出行者对收益和损失的敏感性不同(α,β,λ取值不同),两条路径的前景值有所差异。具体见图 2所示。
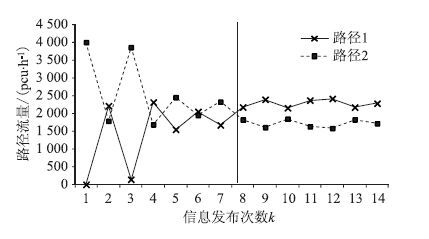
|
| 图 2 t0=0.4 h各路径的流量 Fig. 2 Traffic flow on each route when t0=0.4 h |
| |
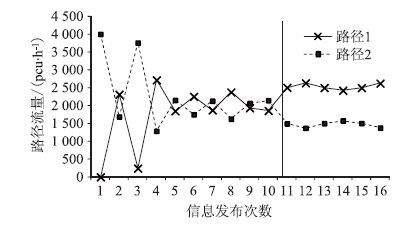
|
| 图 3 t0=0.5 h各路径的流量 Fig. 3 Traffic flow on each route when t0=0.5 h |
| |
② t0=0.5 h,路径的流量变化情况如图 3所示,与图 2比较相似。但是,事故消散持续时间增加,当k=11时(66 min),事故完全消散。期望出行时间t0增大,则出行者所受约束更小,路径1的选择概率增加。相比图 2,图 3中路径1的流量比图 2中路径1的流量大,则事故消散更长。事故消散后,两条路径的流量基本趋于稳定,由于各出行者的α,β,λ取值不同,导致流量有轻微的波动。
(2) 试验对比
试验对象:30名年龄为22~35岁之间的被试者。
试验过程:首先给出两条路径的基本信息,然后模拟VMS信息板计算并第1次发布事故消散时间,请被试者做出选择;统计被试者的选择结果,告知被试者两条路径的选择结果,并第2次计算事故还需的消散时间,请被试者做出选择。
试验结束:直到两条路径流量波动较小,且稳定在同一趋势。
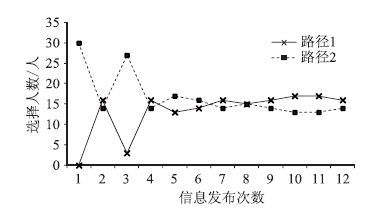
|
| 图 4 t0=0.4 h各路径的选择人数 Fig. 4 Persons on each route when |
| |
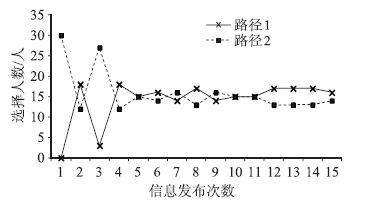
|
| 图 5 t0=0.5 h各路径的选择人数 Fig. 5 Persons on each route when t0=0.5 h |
| |
对比图 2、图 3和图 4、图 5,可以发现计算机仿真与试验结果的趋势基本一致。从试验结果来看,事故发生的初期,两条路径的流量变化较大,随着事故的消散,两条道路之间的流量差逐渐减小,其中在某一个或两个时间间隔出现了两者之间流量相等的现象,然后趋势基本稳定在路径1的流量大于路径2 的流量。与仿真结果稍有差异的是,试验结果得到的事故消散时间(流量趋势基本稳定的时间)均比计算机仿真结果得到的事故消散时间长,分别为54 min(t0=0.4 h)、72 min(t0=0.5 h)。主要原因在于计算机仿真时假设每个人对收益或风险的敏感性是相同的,但是实际上出行者之间各有差异,导致试验结果与仿真有所差异。下一步的研究重点在于出行者有限理性程度的量化建模,以更加准确地衡量出行者的有限理性。
4 结论出行者行为建模一直是交通领域研究的热点,从行为经济学角度提出的前景理论考虑了不同出行者对收益和损失具有不同的敏感性,对路径的效用度量更加符合实际。本文研究了突发交通事故时出行者的路径选择行为,采用连续离散的方式计算其前景值,并设计了一个场景进行实例分析。研究发现,出行者在路径选择中会根据其他出行者的选择结果调整自己的方案,事故消散时间不仅与交通量大小有关,也与出行者的期望出行时间有关,将出行心理与事故延误联系起来,可很好地刻画出行者的路径选择决策过程。
| [1] | SIMON H A. A Behavioral Model of Rational Choice[J]. Quarterly Journal of Economics, 1955, 69 (1) : 99–118 . |
| [2] | KAHNEMAN D, TVERSKY A. Prospect Theory: An Analysis of Decision under Risk[J]. Econometrica: Journal of the Econometric Society, 1979, 47 (2) : 263–292 . |
| [3] | AVINERI E. The Effect of Reference Point on Stochastic Network Equilibrium[J]. Transportation Science, 2006, 40 (4) : 409–420 . |
| [4] | CONNORS R D, SUMALEE A. A Network Equilibrium Model with Travellers' Perception of Stochastic Travel Times[J]. Transportation Research Part B: Methodological, 2009, 43 (6) : 614–624 . |
| [5] | 张波, 隽志才, 林徐勋. 基于累积前景理论的随机用户均衡交通分配模型[J]. 西南交通大学学报,2011,46 (5) :868–874. 868-874. ZHANG Bo,JUAN Zhi-cai,LIN Xu-xun[J]. Stochastic User Equilibrium Model Based on Cumulative Prospect Theory, 2011, 46 (5) : 868–874 . |
| [6] | 徐红利, 周晶, 徐薇. 考虑参考点依赖的随机网络用户均衡与系统演化[J]. 系统工程理论与实践,2010,30 (12) :2283–2289. XU Hong-li, ZHOU Jing, XU Wei. Stochastic Network User Equilibrium and System Evolution with Dependence on Reference Point[J]. Systems Engineering-Theory & Practice, 2010, 30 (12) : 2283–2289 . |
| [7] | 刘玉印, 刘伟铭, 田世艳. 出行者有限理性条件下混合策略网络均衡模型[J]. 公路交通科技,2011,28 (7) :136–141. LIU Yu-yin, LIU Wei-ming, TIAN Shi-yan. Network Equilibrium Model with Mixed Strategies under Bounded Rationality[J]. Journal of Highway and Transportation Research and Development, 2011, 28 (7) : 136–141 . |
| [8] | WANG G C, MA S F, JIA N. A Combined Framework for Modeling the Evolution of Traveler Route Choice under Risk[J]. Transportation Research Part C: Emerging Technologies, 2013 : 156–179 . |
| [9] | SONG G, EMMA F, MOSHE B A. Adaptive Route Choices in Risky Traffic Networks: A Prospect Theory Approach[J]. Transportation Research Part C: Emerging Technologies, 2010, 18 (5) : 727–740 . |
| [10] | 夏金娇, 隽志才, 高晶鑫. 基于前景理论的出行路径选择行为[J]. 公路交通科技,2012,29 (4) :126–131. XIA Jin-jiao, JUN Zhi-cai, GAO Jing-xin. Travel Routing Behaviors Based on Prospect Theory[J]. Journal of Highway and Transportation Research and Development, 2012, 29 (4) : 126–131 . |
| [11] | 胡晓伟, 王健, 孙广林. 有限理性下出行者方式选择行为[J]. 哈尔滨工业大学学报,2011,43 (12) :114–118. HU Xiao-wei, WANG Jian, SUN Guang-lin. Travel's Model Choice Behavior Analysis under Bounded Rational[J]. Journal of Harbin Institute of Technology, 2011, 43 (12) : 114–118 . |
| [12] | ERKE A, SAGBERG F, HAGMAN R. Effects of Route Guidance Variable Message Signs (VMS) on Driver Behavior[J]. Transportation Research Part F: Traffic Psychology and Behavior, 2007, 10 (6) : 447–457 . |
| [13] | GUATTARI C, DE BLASIIS M R, CALVI A. The Effectiveness of Variable Message Signs Information: A Driving Simulation Study[J]. Procedia-Social and Behavioral Sciences, 2012 : 692–702 . |
| [14] | MA Z L, SHAO C F, SONG Y, et al. Driver Response to Information Provided by Variable Message Signs in Beijing[J]. Transportation Research Part F: Traffic Psychology and Behavior, 2014 : 199–209 . |
| [15] | QIN L, SMITH B. Characterization of Accident Capacity Reduction[R]. Charlottesville, VA: Center for Transportation Studies, University of Virginia, 2001. |
| [16] | 陈艳艳, 王光远. 考虑供需随机性的道路交通系统震害引发损失期望评估[J]. 世界地震工程,2003,19 (1) :25–30. CHEN Yan-yan, WANG Guang-yuan. The Estimation of Indirect Loss Expectation after Earthquake Considering Randomness of Traffic Demand and Supply[J]. World Earthquake Engineering, 2003, 19 (1) : 25–30 . |
| [17] | TVERSKY A, KAHNEMAN D. Advances in Prospect Theory: Cumulative Representation of Uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5 (4) : 297–323 . |
| [18] | NEILSON W, STOWE J. A Further Examination of Cumulative Prospect Theory Parameterizations[J]. Journal of Risk and Uncertainty, 2002, 24 (1) : 31–46 . |
 2016, Vol. 33
2016, Vol. 33
