扩展功能
文章信息
- 丁闪闪, 王维锋, 季锦章, 党倩
- DING Shan-shan, WANG Wei-feng, JI Jin-zhang, DANG Qian
- 基于时空关联和BP_Adaboost的短时交通参数预测
- Short-term Traffic Parameter Prediction Based on Spatio-temporal Correlation and BP_Adaboost
- 公路交通科技, 2016, 33(5): 98-104
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 98-104
- 10.3969/j.issn.1002-0268.2016.05.016
-
文章历史
- 收稿日期:2015-03-19
2. 交通运输部智能交通技术和设备行业研发中心, 江苏 南京 210014
2. Intelligent Transport Technology and Equipment Research and Development Center, Ministry of Transport, Nanjing Jiangsu 210014, China
先进的交通控制系统、路径诱导系统和出行者信息系统是交通运营和管理的重要组成部分,而实时准确的短时交通参数预测是实现交通控制、诱导和提供实时交通信息服务的前提和关键[1]。
目前,国内外关于短时交通参数预测的研究成果较多,传统的预测方法大多是基于交通参数的时间关联性开展的,随着数据处理和分析能力的加强,人们逐渐将更多的影响因素引入交通参数的预测中,以提高预测精度,其中考虑最多的是交通参数的空间关联性。Wanli等[2]根据预测时间间隔内车辆的可达性确定空间关联路段,然后将这些路段的历史交通参数数据加入预测模型中;Wu等[3]采用时空随机效应模型进行城市道路路段交通流量的预测,不仅考虑了目标路段的历史交通参数,还考虑了多个参考点的交通参数;于滨等[4]考虑目标路段上下游的历史交通参数数据,构建了时空参数模型进行交通参数预测;邱敦国等[5]采用SARIMA模型通过历史数据预测下一时刻的交通流,然后将预测值与该点上下游关联的交通流数据结合,作为预测模型的输入。对空间关联性的考虑在一定程度上提高了预测精度,但同时也增加了计算复杂度,因此如何合理选择影响因素是平衡该问题的关键,在以往的研究中对这方面考虑较少。
交通参数预测模型主要可以分为两类:统计模型和人工智能模型[6]。在人工智能模型中,前馈神经网络由于具有良好的适应性和较高的精度,因此得到了广泛的应用[7]。针对常规的BP神经网络具有容易陷入局部极小值和收敛速度慢的缺点,部分学者提出采用优化算法对其进行改进,主要包括遗传算法、粒子群算法、蚁群算法、Adaboost算法等[8-12]。其中Adaboost算法是Boosting算法的典型应用之一,其核心思想是针对同一个训练集训练不同的分类器,即弱分类器,然后把这些弱分类器集合起来,构造一个更强的最终分类器。Adaboost算法早期主要用于解决分类和回归问题,近年来开始逐渐应用于预测领域。本文中采用Adaboost算法对BP神经网络进行优化,构建BP_Adaboost预测模型。
本文首先通过时空关联性分析得到对预测值产生影响的因素;然后采用主成分分析法对影响因素进行预处理,选取主成分;接着构建BP_Adaboost预测模型,以选取的主成分作为模型输入,得到交通参数预测值;最后进行试验分析,对提出的方法进行验证。
1 理论方法 1.1 影响因素分析以交通流量发生较大变化的位置为节点,可以将路网中的道路分为多个路段,在城市路网中,通常以较大的交叉口为节点进行路段划分。由于交通需求的周期性变化和交通系统的动态流动性,使得路段上的交通参数具有可预测的特征。不同时段的交通参数存在一定的时间关联性,而不同路段的交通参数又存在一定的空间关联性。交通参数的时间关联性主要体现在两个方面:(1) 当前时段的交通流在某种程度上可以看作是上一时段交通流的延续;(2) 当前时段的交通流在某种程度上可以看作是相似模式下历史交通流的周期性重复。交通参数的空间关联性主要体现在:交通流同时受到其上游路段交通流产生的正向冲击波和下游路段交通流产生的反向冲击波的影响。
基于此,本文根据时空关联性,选取3类要素因子来标定影响因素,分别命名为时间要素因子(相邻时段的影响)、周期要素因子(周期性重复的影响)和空间要素因子(相邻路段的影响)。以xs,t表示目标路段s在t时段的交通参数值;${\tilde x_{s,t + 1}}$表示下一时段(即t+1时段)该路段该参数的预测值;xs,t(i,j,k)表示影响因素,其中i表示与时段t具有时间关联性的第i个时段,即第i个时间要素因子,i=0,1,2,…,M,这里以i=0表示预测时段,即t+1时段;j表示与当前日具有相似模式的第j个历史日(含当前日),即第j个周期要素因子,j=1,2,…,N,这里以j=1表示当前日;k表示与路段s具有空间关联性的第k条路段,即第k个空间要素因子,k=1,2,…,P。当j=1时,t+1时段各路段的数据尚未获取,因此无法利用,当j≠1时,t+1时段的数据可以利用。因此,初步确定的影响因素为MNP+P(N-1)个,如图1所示。
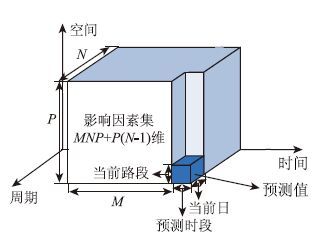
|
| 图 1 影响因素集 Fig. 1 Influencing factor set |
| |
在城市道路中,上游和下游路段的交通流都可能会对目标路段的交通流产生影响,因此,本文选择目标路段以及与其相邻的所有上下游路段作为空间要素因子,如图2所示,该目标路段的空间要素因子有6个。
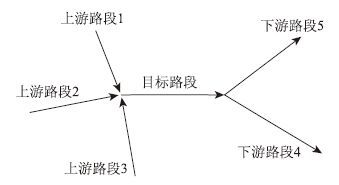
|
| 图 2 空间要素因子示意图 Fig. 2 Schematic diagram of space factors |
| |
1.2 基于主成分分析的影响因素预处理
主成分分析法(Primary Component Analysis,PCA)是通过降维过程,将多个相关联的数值指标转化为少数几个互不相关的综合指标的统计方法[13]。令m=MNP+P(N-1), 为便于表达,以yi表示第i个样本对应的交通参数预测值,以yi(j)表示第i个样本的第j个影响因素,i=1,2,…,n,j=1,2,…,m,则采用主成分分析法进行影响因素降维的步骤如下:
(1) 构建影响因素矩阵:
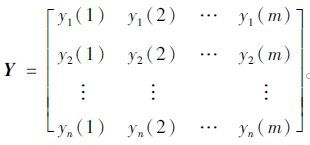
|
(1) |
(2) 影响因素矩阵标准化。标准化公式为:
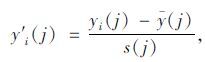
|
(2) |
式中,y′i(j)为yi(j)标准化后得到的值;$\bar y(j)$和s(j)分别为第j个影响因素的平均值和标准差。
标准化后得到新的矩阵为:
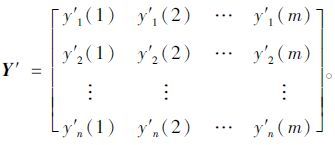
|
(3) |
(3) 计算矩阵Y′的相关系数矩阵:
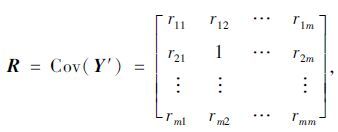
|
(4) |
式中rij为相关系数,rij
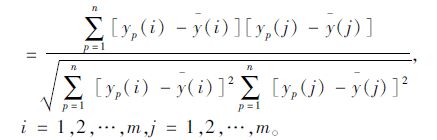
|
(4) 计算R的特征值和特征值对应的特征向量,计算各成分。得到m个非负特征值λj(j=1,2,…,m)及其对应的特征向量lji=[lj1,lj2,…,ljm]T,其中,λ1≥λ2≥…≥λm≥0,从而得到第k(1≤k≤m)个成分zk为:
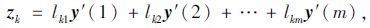
|
(5) |
式中y′(j)=[y′1(j),y′2(j),…,y′n(j)]T。
(5) 计算成分的累积方差贡献率ck。计算公式为:
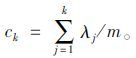
|
(6) |
一般来说,可以根据特征值的大小(以大于等于1为准则)或者累积方差贡献率(大于70%)来选取主成分。在进行预测模型构建时,可以将两种方法相结合,以同时确保预测精度和减少计算复杂度。
1.3 BP_Adaboost交通参数预测模型构建基于BP_Adaboost的短时交通参数预测模型,预测流程如图3所示。
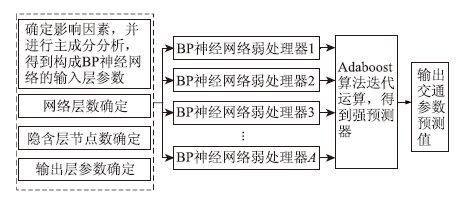
|
| 图 3 基于BP_Adaboost的短时交通参数预测流程 Fig. 3 Short-term traffic parameter prediction process based on BP_Adaboost |
| |
具体实现步骤如下:
(1) 确定单一BP神经网络的结构。包括输入层参数的确定、网络层数选取、隐含层节点数确定和输出层参数确定。其中输入层参数即采用主成分分析法对影响因素进行预处理后得到的主成分,在1.2节介绍其确定方法。对于网络层数,常用的为3层结构,即输入、隐含、输出层均为1层,3层BP神经网络应用最为广泛,且大部分情况下均能满足要求,因此,本文中网络层数选取3层。对于隐含层节点数的确定,根据前人的研究,迄今为止尚未找到一个很好的解析式可以有效解决这一问题[14],本文根据使用较为广泛的Kolmogorov定理,设定隐含层节点数为(2q+1)(q为输入层节点个数),输出层节点数为1,即预测的交通参数值。
(2) 对于样本个数为n的训练集,以Da(i)表示在第a次迭代中样本i的权值,a=1,2,…,A,i=1,2,…,n, 初始化n个样本的分布权值D1(i)=1/n。
(3) 在Da(i)的概率分布下,训练弱预测器ha,计算该弱学习器在各样本下的误差εa(i)。
(4) 设置一个阈值$\hat \varepsilon $,令ea为所有${\varepsilon _a}(i) > \hat \varepsilon $的Da(i)(i=1,2,…,n)之和,计算弱学习器的权值,计算公式为:
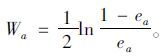
|
(7) |
(5) 更新样本权重:
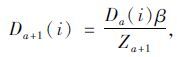
|
(8) |
式中,当${\varepsilon _a}(i) > \hat \varepsilon $时,β>1;当${\varepsilon _a}(i) \leqslant \hat \varepsilon $时, β=1,从而对预测误差较大的样本赋予较大的权重;${Z_{a + 1}} = \sum\limits_{i = 1}^n {{D_{a + 1}}} (i)$。
(6) 跳到步骤(3),进行下一次迭代,直到a=A时结束。
(7) 利用得到的A个弱学习器组合形成强学习器:
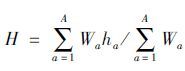
|
(9) |
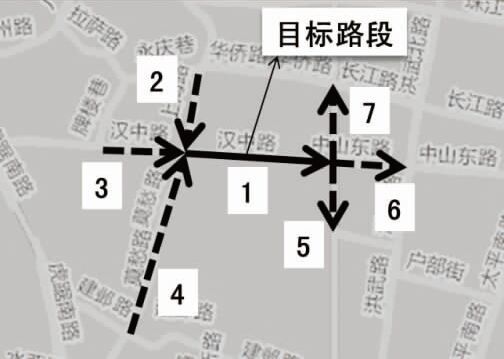
选择南京市汉中路(上海路—中山路路段)作为研究路段,如图4所示。可以看出,与该路段直接相接的有3个上游路段和3个下游路段,对各路段进行编号,如图4中1~7所示,各编号对应影响因素xs,t(i,j,k)中的k值,因此P=7。
|
| 图 4 研究路段 Fig. 4 Research link |
| |
根据从南京市客管处获取的浮动车数据(安装GPS的出租车,以30 s时间间隔上传的经纬度、瞬时速度和方向等数据),可以计算得到每条路段的车辆行驶速度(简称路段速度),采用小波分析法对原始数据进行预处理。以5 min为一个时段,即一个统计时间间隔,进行数据统计和短时交通参数预测。取影响因素集中的M=4(即i=0,1,2,3,4),N=2(即j=1,2),其中i=0,1,2,3,4,分别为预测时段、预测时段的前1个时段、预测时段的前2个时段、预测时段的前3个时段和预测时段的前4个时段;j=1,2,分别为当前日和具有相似交通模式的最近一个历史日。因此考虑时空关联性的影响因素为63个(7×4×2+7×(2-1)=63)。研究表明,交通参数具有较强的星期相似性[15],因此本文以2014年6月份的星期一数据作为试验数据,由于6月2日为端午节,而节假日的交通模式与普通日差别较大,予以剔除,总共得到6月9日、6月16日、6月23日和6月30日4天总共1 152(288×4=1152)组数据。将数据分为两类:由于在试验数据里,6月9日没有历史日的数据可以利用,而6月16日前4组数据没有完整历史时段的数据可以利用,因此总共可以得到860(288×3-4=860)组数据,每组数据中包含64个数据,前63个为影响因素,最后1个为预测值。为了考察在不同交通状态下预测模型的性能,选取每10组数据的最后1组作为测试数据,其他作为训练数据,最后共得到774组训练数据和86组测试数据。
2.2 影响因素预处理以774组训练数据构成影响因素矩阵,按照1.2节中的步骤进行主成分分析,得到各成分的特征值和累积方差贡献率,如表1所示。
| 成分 | 特征值 | 累积方差贡献率/% | 成分 | 特征值 | 累积方差贡献率/% | 成分 | 特征值 | 累积方差贡献率/% | 成分 | 特征值 | 累积方差贡献率/% | |||
| 1 | 47.194 | 27.747 2 | 17 | 0.079 9 | 81.048 6 | 33 | 0.012 9 | 92.330 4 | 49 | 0.003 6 | 97.624 0 | |||
| 2 | 5.081 | 36.852 0 | 18 | 0.071 7 | 82.130 3 | 34 | 0.011 0 | 92.753 5 | 50 | 0.003 5 | 97.861 7 | |||
| 3 | 2.564 | 43.319 5 | 19 | 0.067 1 | 83.176 4 | 35 | 0.010 7 | 93.170 4 | 51 | 0.003 2 | 98.089 7 | |||
| 4 | 1.546 | 48.342 1 | 20 | 0.061 3 | 84.176 2 | 36 | 0.009 2 | 93.558 3 | 52 | 0.003 0 | 98.309 7 | |||
| 5 | 1.241 | 52.841 7 | 21 | 0.053 4 | 85.109 2 | 37 | 0.009 2 | 93.945 7 | 53 | 0.002 4 | 98.508 5 | |||
| 6 | 1.017 | 56.915 8 | 22 | 0.045 3 | 85.968 6 | 38 | 0.009 0 | 94.328 5 | 54 | 0.002 3 | 98.703 2 | |||
| 7 | 0.791 | 60.509 0 | 23 | 0.033 9 | 86.711 8 | 39 | 0.008 3 | 94.696 9 | 55 | 0.002 3 | 98.895 6 | |||
| 8 | 0.663 | 63.797 1 | 24 | 0.030 1 | 87.412 6 | 40 | 0.007 2 | 95.040 3 | 56 | 0.002 2 | 99.083 0 | |||
| 9 | 0.571 | 66.850 3 | 25 | 0.029 0 | 88.100 1 | 41 | 0.007 1 | 95.381 1 | 57 | 0.001 8 | 99.255 6 | |||
| 10 | 0.428 | 69.493 7 | 26 | 0.023 0 | 88.713 2 | 42 | 0.006 3 | 95.702 0 | 58 | 0.001 5 | 99.413 5 | |||
| 11 | 0.329 | 71.811 4 | 27 | 0.020 9 | 89.297 0 | 43 | 0.006 0 | 96.015 8 | 59 | 0.001 5 | 99.569 8 | |||
| 12 | 0.271 | 73.914 5 | 28 | 0.019 4 | 89.859 6 | 44 | 0.005 4 | 96.311 3 | 60 | 0.001 2 | 99.709 3 | |||
| 13 | 0.179 8 | 75.627 2 | 29 | 0.016 9 | 90.385 5 | 45 | 0.005 2 | 96.601 6 | 61 | 0.000 8 | 99.821 7 | |||
| 14 | 0.135 4 | 77.113 5 | 30 | 0.016 3 | 90.901 9 | 46 | 0.004 7 | 96.878 1 | 62 | 0.000 6 | 99.918 9 | |||
| 15 | 0.125 8 | 78.546 2 | 31 | 0.014 7 | 91.391 0 | 47 | 0.004 0 | 97.132 7 | 63 | 0.000 4 | 100.000 0 | |||
| 16 | 0.113 5 | 79.907 2 | 32 | 0.014 1 | 91.870 9 | 48 | 0.003 8 | 97.380 4 |
从表1中可以看出,各成分的特征值呈迅速衰减的趋势,同时累积方差贡献率的增加幅度也迅速减缓。前6个特征值数值大于1,根据特征值的大小可以选取前6项作为主成分;而前11项成分的累积方差贡献率大于70%,根据累积方差贡献率的大小可以选取前11项作为主成分。因此后续预测模型中输入参数的个数可取6~11个。
2.3 预测模型参数设置与结果分析为考察输入参数及预测模型的变化对预测性能的影响,设置以下几种情况:(1) 以前6项主成分为输入,采用BP_Adaboost预测模型;(2) 以前7项主成分为输入,采用BP_Adaboost预测模型;(3) 以前8项主成分为输入,采用BP_Adaboost预测模型;(4) 以前9项主成分为输入,采用BP_Adaboost预测模型;(5) 以前10项主成分为输入,采用BP_Adaboost预测模型;(6) 以前11项主成分为输入,采用BP_Adaboost预测模型;(7) 以仅考虑时间关联性的9个影响因素为输入(此时,P=1,因此输入参数个数为9个(4×2+1),采用BP_Adaboost预测模型;(8) 以前9项主成分为输入,采用传统BP神经网络预测模型。
设置前6种情况是为了考察以不同的主成分作为输入时对预测性能的影响。设置情况(7)是为了与情况(4)进行对比,以考察在预测模型计算复杂度相同条件下,本文提出的方法与传统的仅考虑时间关联性的方法比较,是否能改善预测性能;设置情况(8)是为了与情况(4)进行对比,以考察本文采用的BP_Adaboost预测模型与传统的BP神经网络预测模型比较,是否能改善预测性能。
按照1.3节中的介绍进行隐含层节点数的选取。在神经网络模型中,采用sigmoid函数(trainsig)作为输入层到隐含层的传递函数,采用线性函数(purelin)作为隐含层到输出层的传递函数,采用带动量的梯度下降法(traingdm)作为神经网络的训练函数,神经网络的学习速率设置为0.1,最大训练次数设置为1 000,误差目标值设置为0.001。在BP_Adaboost模型中,取步骤(4)中的阈值$\hat \varepsilon = 0.1$,在步骤(5)中,当${\varepsilon _a}(i) > \hat \varepsilon $时,β=1.1,在式(9)中,A=10。
采用如下指标对预测结果进行评价,分别为平均绝对误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)。前两项用以评价模型的准确性,最后一项用以评价模型的稳定性。各指标的计算公式如下:
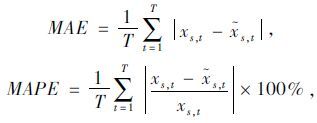
|
(10) |
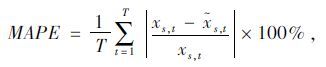
|
(11) |
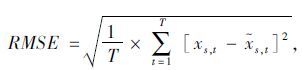
|
(12) |
式中,T为样本数;${{\tilde x}_{s,t}}$为目标路段s在t时段的交通参数预测值。
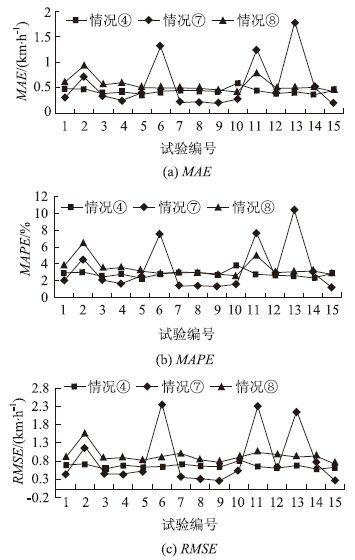
考虑到神经网络模型的预测结果存在一定的不稳定性,因此对于设置的8种情况中的每一种均进行15次试验,取平均值作为最后的结果,如表2所示。情况(4)、(7)、(8)对应的各试验下3个性能指标的变化情况如图5所示。
| 设置情况 | MAE/(km·h-1) | MAPE/% | RMSE/(km·h-1) |
| (1) | 0.662 4 | 4.09 | 0.880 0 |
| (2) | 0.561 6 | 3.39 | 0.800 2 |
| (3) | 0.508 8 | 3.13 | 0.725 1 |
| (4) | 0.435 3 | 2.73 | 0.663 2 |
| (5) | 0.407 0 | 2.57 | 0.667 8 |
| (6) | 0.436 3 | 2.78 | 0.703 3 |
| (7) | 0.554 5 | 3.28 | 0.854 6 |
| (8) | 0.552 5 | 3.36 | 0.935 8 |
|
| 图 5 三种情况下的预测性能变化 Fig. 5 Prediction performance changes in 3 situations |
| |
(1) 选择不同的主成分作为输入时,预测性能有所差异,当选取的主成分个数为10个左右时,预测性能最好。
(2) 在保证预测模型计算复杂度相同的情况下,情况(4)比情况(7)的MAE,MAPE,RMSE分别降低了0.119 2 km/h,0.55%,0.191 4 km/h左右。从图5中可以发现,在多次试验中,情况(4)的各项性能指标值变化波动较小,而情况(7)的各项性能指标值变化波动剧烈。由此可见,本文提出的方法不仅能够在一定程度上提高预测精度,更重要的是能极大地增加预测结果的稳定性。
(3) 在采用同样的输入参数的情况下,情况(4)比情况(8)的MAE,MAPE,RMSE分别降低了0.117 2 km/h,0.63%,0.272 6 km/h左右。从图5中可以发现,在多次试验中,两种情况下的各项性能指标值变化波动均较小,但是除极少数外,几乎在所有的试验中,情况(4)的各项性能指标值都优于情况(8)。
3 结论传统的预测方法多是仅考虑交通参数的时间关联性,部分对时空关联性进行考虑的方法中也未能对影响因素进行预处理和选择,以降低计算复杂度。本文提出了一种基于时空关联分析和BP_Adaboost的短时交通参数预测方法,通过主成分分析法对影响因素进行综合和主成分选取,将得到的主成分输入BP_Adaboost模型中进行参数预测。试验结果表明,该方法可以在一定程度上提高预测精度,并极大地增加预测结果的稳定性,与仅考虑时间关联性以及传统的BP神经网络方法比较,该方法具有一定的优势。
| [1] | 张晓利, 陆化普. 非参数回归方法在短时交通流预测中的应用[J]. 清华大学学报:自然科学版,2009,49 (9) :1471–1475. ZHANG Xiao-li, LU Hua-pu. Non-parametric Regression and Application for Short-term Traffic Flow Forecasting[J]. Journal of Tsinghua University: Science and Technology Edition, 2009, 49 (9) : 1471–1475 . |
| [2] | MIN W, WYNTER L. Real-time Road Traffic Prediction with Spatio-temporal Correlations[J]. Transportation Research Part C, 2011, 19 (4) : 606–616 . |
| [3] | WU Y J, CHEN F, LU C T, et al. Traffic Flow Prediction for Urban Network Using Spatio-temporal Random Effects Model[C]//91st Annual Meeting of the Transportation Research Board(TRB). [S. l.]: TRB, 2012. |
| [4] | 于滨, 邬珊华, 王明华, 等. K近邻短时交通流预测模型[J]. 交通运输工程学报,2012,12 (2) :105–111. YU Bin, WU Shan-hua, WANG Ming-hua, et al. K-nearest Neighbor Model of Short-term Traffic Flow Forecast[J]. Journal of Traffic and Transportation Engineering, 2012, 12 (2) : 105–111 . |
| [5] | 邱敦国, 兰时勇, 杨红雨. 基于时空特性的短时交通流预测模型[J]. 华南理工大学学报: 自然科学版,2014,42 (7) :49–54. QIU Dun-guo, LAN Shi-yong, YANG Hong-yu. Short-Term Traffic Flow Forecast Model Based on Temporal-Spatial Characteristics[J]. Journal of South China University of Technology: Natural Science Edition, 2014, 42 (7) : 49–54 . |
| [6] | 聂庆慧, 夏井新, 钱振东. 城市道路交通流短时预测及可靠性分析[J]. 西南交通大学学报,2013,48 (5) :955–960. NIE Qing-hui, XIA Jing-xin, QIAN Zhen-dong. Short-term Traffic Flow Forecasting and Reliability Analysis of Urban Road[J]. Journal of Southwest Jiaotong University, 2013, 48 (5) : 955–960 . |
| [7] | KARLAFITIS M G, VLAHOGIANNI E I. Statistical Methods versus Neural Networks in Transportation Research: Difference, Similarities and Some Insights[J]. Transportation Research Part C: Emerging Technologies, 2011, 19 (3) : 387–399 . |
| [8] | VLAHOGIANNI E I, KARLAFTIS M G, GOLIAS J C. Optimized and Meta-optimized Neural Networks for Short-term Traffic Flow Prediction: A Genetic Approach[J]. Transportation Research Part C: Emerging Technologies, 2005, 13 (3) : 211–234 . |
| [9] | ZHONG M, SHARMA S, LINGRAS P. Short-term Traffic Prediction on Different Types of Roads with Genetically Designed Regression and Time Delay Neural Network Models[J]. Journal of Computing in Civil Engineering, 2005, 19 (1) : 94–103 . |
| [10] | 李松, 刘力军, 翟曼. 改进粒子群算法优化BP神经网络的短时交通流预测[J]. 系统工程理论与实践,2012,32 (9) :2045–2049. LI Song, LIU Li-jun, ZHAI Man. Prediction for Short-term Traffic Flow Based on Modified PSO Optimized BP Neural Network[J]. Systems Engineering-Theory & Practice, 2012, 32 (9) : 2045–2049 . |
| [11] | 闫伟, 刘云岗, 王桂华, 等. 基于数据挖掘的交通流预测模型[J]. 系统工程理论与实践,2010,30 (7) :1320–1325. YAN Wei, LIU Yun-gang, WANG Gui-hua, et al. Data Mining Using in a Novel Traffic Flow Forecasting Model[J]. Systems Engineering-Theory & Practice, 2010, 30 (7) : 1320–1325 . |
| [12] | 陈淑燕, 王炜, 瞿高峰, 等. 交通量预测的神经网络集成方法[J]. 公路交通科技,2004,21 (12) :80–83. CHEN Shu-yan, WANG Wei, QU Gao-feng, et al. Traffic Flow Forecast Based on Neural Network Ensemble[J]. Journal of Highway and Transportation Research and Development, 2004, 21 (12) : 80–83 . |
| [13] | 林杰斌, 刘明德. SPSS10与统计模式建构. 北京: 中国统计出版社[M]. 2001 : 185 -190. LIN Jie-bin, LIU Ming-de. SPSS10.0 and Construction of Statistics Model. Beijing: China Statistics Press[M]. 2001 : 185 -190. |
| [14] | 李瑞敏, 陈熙怡. 多源数据融合的道路旅行时间估计方法研究[J]. 公路交通科技,2014,31 (2) :99–103. LI Rui-min, CHEN Xi-yi. Study on Methods of Travel Time Estimation Based on Multi-source Data Fusion[J]. Journal of Highway and Transportation Research and Development, 2014, 31 (2) : 99–103 . |
| [15] | WILLIAMS B M. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal Stochastic Time Series Process[D]. Charlottesville, VA: University of Virginia, 1999. |
 2016, Vol. 33
2016, Vol. 33
