扩展功能
文章信息
- 柴生波, 王秀兰, 任翔
- CHAI Sheng-bo, WANG Xiu-lan, REN Xiang
- 三塔两跨悬索桥中塔位移及跨中挠度简化计算方法
- A Simplified Calculation Method for Middle Pylon Deformation and Mid-span Deflection in Three-pylon and Two-span Suspension Bridge
- 公路交通科技, 2016, 33(5): 85-91
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 85-91
- 10.3969/j.issn.1002-0268.2016.05.014
-
文章历史
- 收稿日期:2015-06-08
2. 长安大学 公路学院, 陕西 西安 710061
2. School of Highway, Chang'an University, Xi'an Shaanxi 710061, China
多跨悬索桥在跨越宽阔河流、海峡时具有明显优势,泰州长江大桥和马鞍山大桥的建造标志着多塔连跨悬索桥这一新型桥梁结构的崛起。然而,由于多塔体系桥梁中间桥塔缺乏边跨主缆的有效约束,不平衡活载作用下,加劲梁的竖向挠度较大,加劲梁竖向挠跨比成为控制多塔悬索桥设计的重要技术指标。随着计算手段的进步,采用有限元等数值计算方法可以较为准确地计算桥梁变形与受力,但是多塔悬索桥的设计参数较多,初步设计阶段采用数值模拟来优化设计参数往往需要进行大量计算,若能够采用解析方法对结构变形进行估算,既可以避免复杂的参数分析,提高工作效率,又可以使设计者更好地了解其力学特性,简化设计流程,因此,研究多塔悬索桥的简化计算方法十分必要[1-3]。
对于大跨度悬索桥,主缆的力学行为决定着整个结构的力学行为。国内外许多学者对主缆在活载作用下的变形和受力进行了研究[1-6]。Clemente[1]研究了大跨度悬索桥主要设计参数对结构力学性能的影响,研究发现,随着跨径的增大,悬索桥的力学特性越来越接近主缆的力学特性。Jennings[2]以线性挠度理论为基础,忽略活载对主缆内力的影响,研究了集中荷载及均布荷载下主缆的变形,但未考虑桥塔刚度的影响。Wollmann[3]以挠度理论为基础,提出了一套计算加劲梁挠度及弯矩的实用方法。Gimsing[4]对均布荷载及集中荷载下的主缆变形进行了数值研究,探讨了活载作用下主缆变形的规律。也有学者对悬索桥的重力刚度进行了研究,得到了集中荷载下主缆竖向变形的解析计算公式[5-6]。以上研究主要针对传统两塔悬索桥,由于多跨悬索桥存在“中塔效应”,其力学特性与传统两塔悬索桥有明显差异,以上成果直接用于对多跨悬索桥的分析。
悬索桥主缆对桥塔的约束效应是影响结构变形的重要因素,许多学者对此进行了研究[7-10]。Yoshida[7]研究了多塔悬索桥中跨主缆对桥塔的约束,给出了中跨主缆对桥塔约束的公式。柴生波等[8]运用能量法研究了缆塔约束,给出了缆塔约束解析计算公式。Kiureghian和Sackman等[9]假定索的线形为抛物线,忽略索的弹性伸缩,推导了倾斜索在自重作用下沿各个方向的切线几何刚度。Choi Dong-ho[10]通过假定悬索桥主缆线形为抛物线,通过变分原理推导了倾斜拉索的纵桥向刚度,提出用于分析多塔悬索桥桥塔变形及受力的简化力学模型。以上针对缆塔约束效应的研究成果有助于对悬索桥力学特性的理解,同时也为多跨悬索桥变形解析计算方法的研究奠定了理论基础。
本文综合研究活载下的主缆变形及缆塔约束效应,推导单个主跨满布均布荷载时三塔悬索桥的最大挠度及塔顶位移解析计算公式,并通过有限元模型对公式的准确性进行验证。
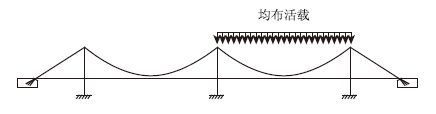
1 主缆变形的解析方法三塔悬索桥变形的最不利加载模式是一个主跨满布活载,其余各跨空载[11-12](如图 1所示),此时中塔承受的不平衡水平力最大,塔顶位移及加劲梁挠度均达到最大。我国现有规范中尚没有针对大跨度多塔悬索桥设计荷载的明确规定,目前国外的研究者对多跨悬索桥的研究中采用均布荷载的加载模式[10, 12-13],这种加载方式是合理的,因为大跨度多跨悬索桥中,仅对其中一个主跨满跨布载已是一种极端工况,因此施加均布荷载后,不必再在其最不利位置施加集中力。本文研究中将沿用这种加载方式。
|
| 图 1 三塔两跨悬索桥最大变形加载工况 Fig. 1 Load condition for maximum deflection of 3-pylon and 2-span suspension bridge |
| |
本文分析时,采用如下假定:
(1) 恒载状态下,主缆线形为抛物线;
(2) 吊杆沿纵桥向密布,忽略吊杆的弹性伸缩,并且吊杆在恒载及活载作用下均保持竖直;
(3) 大跨度悬索桥中,加劲梁刚度对结构变形的影响远小于重力刚度的影响,因此研究中忽略加劲梁的刚度对结构变形的影响;
(4) 边跨主缆对边塔的纵向约束较强,活载作用下,边塔位移远小于中塔位移,假定活载作用下边塔位移为0。
忽略吊杆的伸缩,单个桥跨满布均布活载时,加劲梁竖向挠度与主缆竖向变形相等,通过求解主缆垂度改变即可得到加劲梁竖向挠度。活载q作用下(图 1),加载跨主缆垂度改变主要由两部分构成:一部分是由均布活载作用导致主缆弹性伸长引起的垂度改变δf1;另一部分是由中塔纵向位移引起的垂度改变δf2,故加劲梁总的挠度δf可表示为:
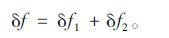
|
(1) |
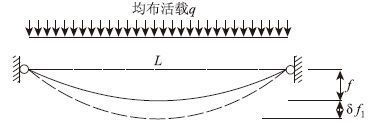
恒载状态下,主缆跨度为L,垂度为f,所受恒载集度为Q,沿跨长施加均布活载q,均布活载q引起的垂度改变为δf1(图 2所示)。
|
| 图 2 满跨均布荷载下主缆变形 Fig. 2 Deformation of main cable under uniform live load acting on full span |
| |
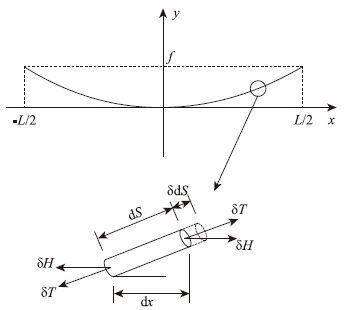
主缆总体线形为抛物线,坐标系如图 3选取,主缆线形可表示为:
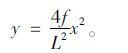
|
(2) |
|
| 图 3 主缆线形及微段 Fig. 3 Cable shape and its micro-sagment |
| |
施加均布荷载后,沿桥跨方向取长度为dx的主缆微段进行研究(见图 3),dx对应的主缆长度dS可表示为:
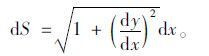
|
(3) |
恒载作用下,主缆水平力H为H=QL2/8f。活载q引起的主缆水平力增量δH为:
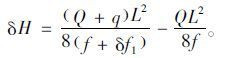
|
(4) |
图 3中主缆微段的内力增量δT与其水平分力增量δH的关系可表示为:
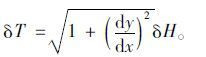
|
(5) |
由主缆内力增加引起的微段伸长量δdS为:
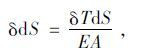
|
(6) |
式中,E,A
将式(3)、(5)代入式(6)中,得
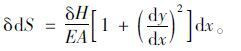
|
(7) |
δdS为微段主缆伸长量,沿跨长积分可得主缆总伸长量dS,即:
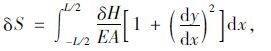
|
(8) |
式中,δH,EA均为常量,因此有:
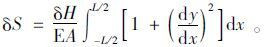
|
(9) |
由式(2)得
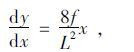
|
(10) |
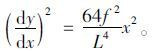
|
(11) |
根据文献[14],主缆变形较小时,主缆伸长量与垂度改变的关系近似为:
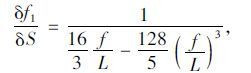
|
(12) |
即
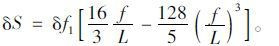
|
(13) |
由式(9)(13),得:
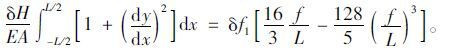
|
(14) |
式(4)代入式(14),得:
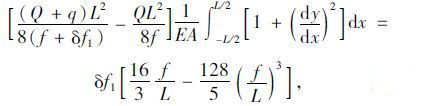
|
(15) |
式中,
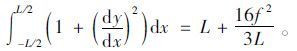
|
(16) |
将式(16)代入式(15),得:
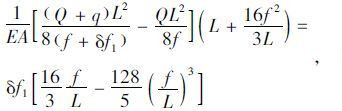
|
(17) |
化简,得:
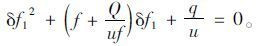
|
(18) |
式中,
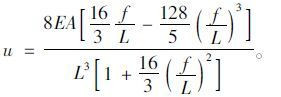
|
(19) |
L,f,E,A,Q等设计参数确定后,根据式(18)和式(19)即可求得均布活载q引起的主缆垂度改变。
式(18)中含恒载Q,计入了恒载对均布活载作用下主缆变形的影响。
1.2.2 未考虑恒载影响的求解方法由于恒载作用下主缆总体线形近似为抛物线,施加均布活载后,主缆线形依然为抛物线,因此,沿跨长施加均布活载时,恒载对主缆线形的稳定作用影响较小。下面推导不考虑恒载作用时,均布活载引起的主缆变形。
在沿跨长的均布荷载作用下,主缆发生弹性伸长,但其线形仍保持为抛物线,文献[14]推导了主缆弹性伸长与垂度改变量的近似关系:
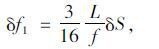
|
(20) |
式中,δS为主缆弹性伸长。
由式(9)、(11)可得,主缆的弹性伸长δS为
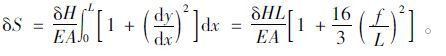
|
(21) |
将式(21)代入式(20),得
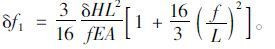
|
(22) |
式(22)是在已知水平力增量δH的情况下求解由主缆弹性伸长引起的垂度增量公式。活载作用引起的主缆水平力增量可近似表示为
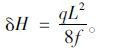
|
(23) |
式(22) 未考虑恒载对均布荷载作用下主缆变形的影响。
1.2.3 公式验证为验证以上公式在求解均布荷载作用下主梁变形的准确性,根据实际悬索桥(长寿长江二桥)建立有限元模型。主缆跨长L=739 m,主缆垂度f=82.1 m,垂跨比为1/9,主缆的弹性模量E=210 000 MPa,面积A=0.404 m2,恒载Q=250 kN/m,均布荷载q=10 kN/m。将以上参数代入式(19)中,计算得u=879.55 N/m3,将以上参数代入式(18),得
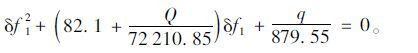
|
(24) |
解式(24),得δf1=0.133 m。有限元计算值为δf1=0.132 m,将L,f,E,A,n,q=10 kN/m代入式(22)中得δf1=0.130 m,式(24)的误差主要来自于主缆水平力增量的计算。
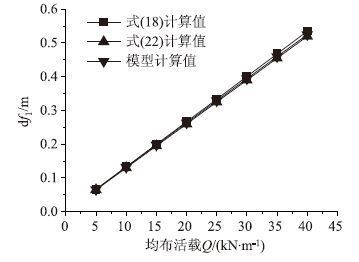
按照以上参数建立主缆有限元模型,初始恒载取为Q=250 kN/m,在沿跨长的均布活载作用下,式(18)、(22)与有限元模型计算值计算结果如图 4所示。
|
| 图 4 均布荷载引起的主缆挠度 Fig. 4 Deflection of cable caused by uniform live load |
| |
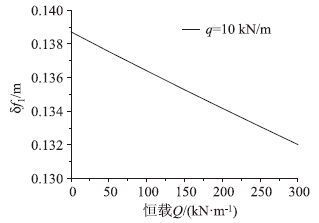
恒载从0增加到250 kN/m,式(18)解得的主缆变形从0.139 m减小到0.133 m,仅减小了4.3%(如图 5所示)。
|
| 图 5 主缆垂度增量随恒载的变化 Fig. 5 Increment of cable sag varying with dead load |
| |
图 4可知,式(18)、(22)计算结果均与有限元模型计算结果较接近,均可较为精确地计算均布活载作用下主缆的变形,由公式的表达形式可知,主缆的变形量主要取决于跨长、垂跨比及主缆的轴向刚度。由图 5可以看出,在满跨均布荷活载作用下,恒载对于主缆变形的影响较小,主缆初始内力对主缆变形的影响可忽略不计。
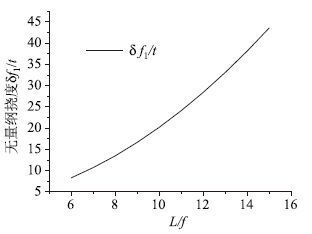
对此可作如下解释,主缆在恒载作用下总体线形为抛物线,沿跨长施加均布活载之后,主缆线形仍为抛物线,主缆变形主要由主缆的弹性伸长所引起,取决于主缆的轴向刚度,而主缆的重力刚度对这种工况下主缆变形影响较小。由式(22)可以看出,在跨长一定的情况下,均布荷载引起的主缆垂度增量主要与主缆的弹性刚度EA以及主缆的垂跨f/L有关。式(22)中,在q,L,EA均确定的情况下,可令qL2/8EA=t,则主缆无量纲挠度δf1/t与L/f的关系如图 6所示
|
| 图 6 均布荷载下主缆无量纲挠度与L/f关系 Fig. 6 Relation of dimensionless deflection of cable and L/f under uniform live load |
| |
由图 6可以看出,沿跨长满布均布荷载作用下,主缆挠度随着跨长垂度比值的增大而增大,即跨长L一定的情况下,主缆垂度f越小,均布荷载引起的主缆挠度越大。
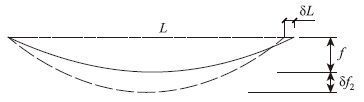
1.3 中塔位移引起的主缆变形三塔两跨悬索桥中其中一个主跨施加均布荷载后,加载跨主缆内力增大,中塔塔顶发生纵向位移δL,塔顶位移导致主缆垂度改变δf2,(图 7)。
|
| 图 7 塔顶位移引起的主缆垂度改变 Fig. 7 Change of cable sag caused by pylon top displacement |
| |
根据文献[15],塔顶位移与主缆垂度改变的关系为
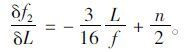
|
(25) |
由于悬索桥垂跨比n较小,式(25)可进一步简化为:
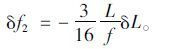
|
(26) |
δL与δf2符号相反,塔顶位移使桥跨增大时,此时主缆垂度减小。
2 三塔两跨悬索桥跨中挠度、中塔位移求解将式(22)、(26)代入式(1)得到活载作用下加劲梁的最大挠度δf,即
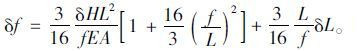
|
(27) |
为方便计算,式(27)中,加劲梁挠度δf以及塔顶位移δL均取正值。式中塔顶位移δH、δL为未知量,下面分别求解。
根据加载跨主缆水平力增量与非加载跨平衡,得
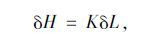
|
(28) |
式中,K为主缆纵向约束刚度Kc及桥塔纵向抗推刚度Kt之和,Kc可近似用式(29)估算[8]
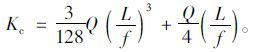
|
(29) |
考虑塔顶位移及垂度改变,加载跨主缆水平力增量为
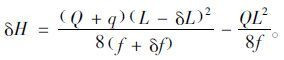
|
(30) |
主缆垂度与桥跨长度相差约一个数量级,但主缆垂度改变量δf大于δL,由于塔顶位移与桥跨长度相比极小,为计算方便,式(30)中可忽略跨长的改变量δL,而δf则不可忽略,由此,式(30)变为
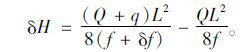
|
(31) |
将式(31)代入式(28)中,可得
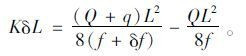
|
(32) |
将式(27)化简,可得
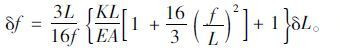
|
(33) |
式(32)、(33)可联立成方程组(34),求解方程组(34)可得加劲梁挠度δf以及塔顶位移δL。
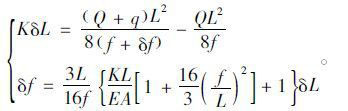
|
(34) |
方程组(34)即为三塔两跨悬索桥其中一跨加载时,塔顶位移及跨中挠度的估算公式,在已知各主要设计参数后,式(34)中,仅δf及δL为未知数,K为主缆纵向刚度Kc(可由式(29)求得)与桥塔抗推刚度Kt之和。
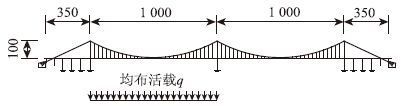
3 模型验证为验证本文公式的准确性,建立三塔两跨悬索桥模型,两个主跨均为1 000 m,主缆垂跨比为1/10,桥塔高度为160 m,桥跨布置如图 8所示,主要构件参数如表 1所示,对其中一个主跨施加均布荷载如图 8所示。
| 主要参数 | 符号 | 数值 |
| 主缆截面积/m2 | A | 2×0.306 8 |
| 中跨主缆垂度/m | f | 100 |
| 主缆、吊索钢箱梁弹模/GPa | Eg | 200 |
| 桥塔混凝土弹模/GPa | Et | 34.5 |
| 加劲梁抗弯惯性矩/m4 | Ig | 2.879 |
| 桥塔抗弯惯性矩/m4 | It | 2×92.7 |
| 桥塔高度/m | h | 160 |
| 桥面系重量(含主缆、吊索)/(kN·m-1) | Q | 279.6 |
|
| 图 8 三塔两跨悬索桥布置图及加载工况(单位:m) Fig. 8 Layout of 3-pylon and 2-span bridge and loading case(unit:m) |
| |
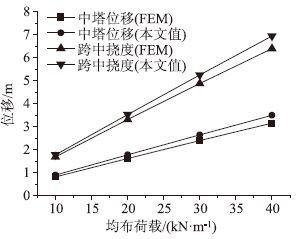
将各参数代入式(29)可得,K=6 884 kN/m,均布荷载q取10 kN/m时,将f=100,L=1 000 m,EA=122 720 000 kN/m,Q=279.6 kN/m代入式(34)可得δf=1.780 m,δL=0.896 m,同理可求得均布荷载为20,30,40 kN/m时的塔顶位移与跨中挠度。图 8加载模式下,中塔位移与加载跨挠度的有限元模型求解值与本文理论值绘于图 9中。为忽略桥塔纵向抗推刚度的影响,模型中释放主缆在塔顶处纵向约束。
|
| 图 9 中塔及跨中挠度(未计桥塔刚度) Fig. 9 Deflections of middle pylon and mid-span (pylon stiffness is omitted) |
| |
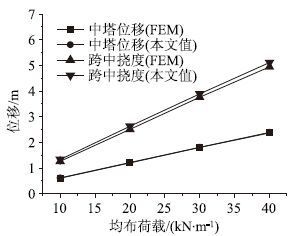
在本模型中,若考虑中塔抗推刚度,单独计算中塔抗推刚度可得中塔刚度为Kt=4 673 kN/m,考虑桥塔的抗推刚度后,K=6 884+6 273=13 157 kN/m。将各参数代入后可得,q=10 kN/m时,δf=1.265 m,δL=0.606 m。同理可得均布荷载为20,30,40 kN/m时的塔顶位移与跨中挠度,本文理论值与有限元模型值如图 10所示。
|
| 图 10 中塔及跨中变形(计入桥塔刚度) Fig. 10 Deformation of middle pylon and mid-span (pylon stiffness is considered) |
| |
图 9表明,加载跨挠度与中塔位移的理论值均与有限元求解值较接近,本文理论值略大,并且误差随着均布荷载的增大而有所增大。当均布荷载取40 kN/m时,跨中挠度的理论值为6.943 m,有限元计算值为6.397 m,误差约为8%,误差来自与本文计算所采用的假定以及推导过程中的简化。同时,在计算主缆纵向约束时,式(29)也会产生一定的误差。
图 10可见,在考虑了桥塔抗推刚度后,跨中挠度与塔顶位移的理论值均与有限元模型值更为接近,均布荷载增大至40 kN/m时,跨中挠度的理论值为4.945 m,模型计算值为5.116 m,误差仅为3%,这是因为考虑桥塔刚度后,边桥塔的位移更加接近于0,与本文的假定更加接近。
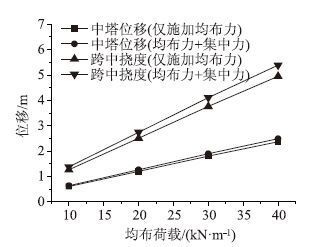
本文为考虑集中力引起的结构变形,若在施加均布荷载的同时,在跨中施加一个集中力(均布荷载取10,20,30,40 kN/m时,集中力分别取360,720,1 080,1 440 kN),则加载跨与中塔最大位移如图 11所示。
|
| 图 11 均布力与集中力引起的中塔及跨中变形(计入桥塔刚度) Fig. 11 Deformations of middle pylon and mid-span under uniform force and concentrated force (pylon stiffness is considered ) |
| |
由图 11可见,考虑集中力后,中塔位移与跨中挠度均有所增大,但二者差别不大。考虑集中力后,中塔位移约增大5%,跨中挠度增大约9%。因此,仅考虑均布荷载基本能够反映三塔两跨悬索桥的变形情况。
在确定了三塔两跨悬索桥的跨长、主缆垂度、单位桥长恒载重量、桥塔抗推刚度等主要设计参数的情况下,式(34)可以估算塔顶位移以及加劲梁最大挠度。进行初步设计时,在确定了最大容许挠度的情况下,式(34)还可以用于反推各主要参数的取值范围。
4 结论本文研究了沿跨长的均布荷载作用下悬索桥主缆的变形,在此基础上推导了均布荷载作用下三塔两跨悬索桥的中塔位移及加劲梁挠度的解析计算公式,通过建立有限元模型对公式精度进行了验证,本文主要获得以下结论:
(1) 在沿跨长的均布荷载作用下,恒载对于减小主缆变形的影响极为有限,主缆垂度的改变主要取决于主缆的轴向刚度以及垂跨比,垂跨比越小,均布荷载引起的主缆挠度就越大。
(2) 三塔两跨悬索桥在单个主跨受到均布荷载作用时,加劲梁(主缆)的变形可分解为塔顶位移引起的变形及主缆弹性伸长引起的变形。在确定了跨长、主缆垂度、恒载集度等主要设计参数之后,通过本文公式可估算塔顶位移及加劲梁的最大挠度。
(3) 本文提供的用于求解三塔两跨悬索桥加劲梁及中塔塔顶位移的解析公式可计入桥塔抗推刚度的影响,本文公式有较高精度,可用于指导初步设计阶段参数的合理取值。
| [1] | CLEMENTE P, NICOLOSI G, RAITHEL A. Preliminary Design of Very Long-span Suspension Bridges[J]. Engineering Structure, 2000, 22 (12) : 1699–1706 . |
| [2] | JENNINGS A. Gravity Stiffness of Classical Suspension Bridges[J]. Journal of Structure Engineering, 1983, 109 (1) : 16–36 . |
| [3] | WOLLMANN G P. Preliminary Analysis of Suspension Bridge[J]. Journal of Bridge Engineering, 2005, 6 (4) : 227–233 . |
| [4] | GIMSING N J. Cable Supported Bridges: Concept and Design [M]. 2nd ed. New York: Wiley, 1997. |
| [5] | 刘钊, 刘厚军. 悬索桥主缆变形及重力刚度新算法[J]. 工程力学,2009,26 (6) :127–132. LIU Zhao, LIU Hou-jun. New Arithmetic for Cable Deflection and Gravity Stiffness of Suspension Bridges[J]. Engineering Mechanics, 2009, 26 (6) : 127–132 . |
| [6] | IRVINE H M. Cable Structures[J]. Cambridge: MIT University Press, 1981 . |
| [7] | YOSHIDA O, OKUDA M, MORIYA T. Structural Characteristics and Applicability of Four-span Suspension Bridge[J]. Journal of Bridge Engineering, 2004, 9 (5) : 453–463 . |
| [8] | 柴生波, 肖汝诚, 张学义, 等. 多跨悬索桥中塔纵向刚度研究[J]. 中国公路学报,2012,25 (2) :67–71. CHAI Sheng-bo, XIAO Ru-cheng, ZHANG Xue-yi, et al. Study of Longitudinal Stiffness of Middle Pylon in Multi-span Suspension Bridge[J]. China Journal of Highway and Transport, 2012, 25 (2) : 67–71 . |
| [9] | KIUREGHIAN A D, SACKMAN J L. Tangent Geometric Stiffness of Inclined Cables Under Self-weight[J]. Journal of Structural Engineering, 2005, 131 (6) : 941–945 . |
| [10] | CHOI D H, GWON S G, NA H S. Simplified Analysis for Preliminary Design of Towers in Suspension Bridge[J]. Journal of Bridge Engineering, 2014, 19 (3) : 165–184 . |
| [12] | 杨进. 多塔多跨悬索桥应用于海峡长桥建设的技术可行性与技术优势[J]. 桥梁建设,2009, (2) :36–39. YANG Jin. Technical Feasibility and Advantages of Applying Multi-tower and Multi-span Suspension Bridge to Construction of Long Bridge across Straits[J]. Bridge Construction, 2009, (2) : 36–39 . |
| [13] | THAI H T, CHOI D H. Advanced Analysis of Multi-span Suspension Bridges[J]. Journal of Constructional Steel Research, 2013, 90 (5) : 29–41 . |
| [14] | CHOI D H, GWON S G, YOO H, et al. Nonlinear Static Analysis of Continuous Multi-span Suspension Bridges[J]. International Journal of Steel Structure, 2013, 13 (1) : 103–115 . |
| [15] | 柴生波, 肖汝诚, 孙斌. 活载下悬索桥主缆变形特性[J]. 同济大学学报:自然科学版,2012,40 (10) :1452–1457. CHAI Sheng-bo, XIAO Ru-cheng, SUN Bin. Deformation Characteristics of Main Cable in Suspension Bridge Caused by Live Load[J]. Journal of Tongji University:Natural Science Edition, 2012, 40 (10) : 1452–1457 . |
 2016, Vol. 33
2016, Vol. 33
