扩展功能
文章信息
- 吕毅刚, 韩伟威, 吕健鸣, 刘云峰
- LÜ Yi-gang, HAN Wei-wei, LÜ Jian-ming, LIU Yun-feng
- 基于暴露试验的桥梁混凝土长期弹性模量试验研究
- Experimental Study on Long-term Elastic Modulus of Bridge Concrete Based on Exposure Experiment
- 公路交通科技, 2016, 33(5): 78-84
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(5): 78-84
- 10.3969/j.issn.1002-0268.2016.05.013
-
文章历史
- 收稿日期:2015-04-20
2. 长沙理工大学 交通运输工程学院, 湖南 长沙 410114
2. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha Hunan 410114, China
近年来,许多国家和地区相继发生了一些严重的混凝土桥梁垮塌灾难性事故,使得桥梁混凝土的长期力学性能问题逐渐引起重视[1-3]。目前对长期力学性能中的弹性模量进行跟踪观测时,主要采用在混凝土试件表面上粘贴应变片,进行静弹性模量测试,其受自身质量及天气的影响较明显,试验工作量很大,费时费力[4],同时受地理条件及自然环境的限制,一般只能在实验室内进行,方便性很差。
混凝土的性质也可采用动弹性模量描述,各国学者开始探索混凝土的动弹性模量研究[5-7]。Sang-Hun Han、Jin-Keun Kim[8]通过试验研究,发现水泥种类对混凝土动、静弹性模量之间的关系影响不显著。施士昇[9]通过大量的试验研究,发现高强混凝土的动、静弹性模量关系与普通混凝土之间的两者关系接近。郑永来、周澄、黄炜等[10-11]基于不同悬臂梁结构振动试验的试验结果,构建了动态弹性模量随频率变化的理论模型。刘宏伟、谢丽、吴胜兴等[12]进行了混凝土的早龄期动弹性模量研究,发现相对于混凝土自身密度和泊松比而言,超声波波速对动弹性模量的影响较大。张建仁、唐腾、彭晖等[13]利用了一种采用纵波换能器检测混凝土的纵波及表面波的波速,从而测量其动弹模量的技术。此外,孙丛涛、牛荻涛、元成方等[14]通过试验研究,建立了混凝土动弹性模量与超声声速的相互关系。目前对28 d标准龄期的桥梁混凝土动弹性模量的相关研究较多,且骨料组成成分较为单一,而对桥梁混凝土的长期弹性模量研究非常少。由于长期力学性能是一个与环境相关的不确定变量,而实际混凝土桥梁结构处于复杂的自然环境之中,与室内环境条件相差甚远。在以后研究中,如何扩大骨料的应用范围,更进一步建立桥梁混凝土动、静态弹性模量之间的换算关系,并对实际桥梁构件的长期弹性模量进行无损跟踪观测,是一个迫切需要解决的课题。为此,本研究建立暴露试验站,对一批碎石混凝土试件和钢筋混凝土构件进行长期跟踪观测,采用超声波平测法,开展桥梁混凝土长期动、静弹性模量试验研究。
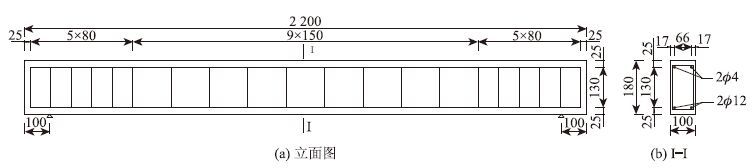
1 暴露试验站简介在一般桥梁生存环境中建立了暴露试验站。首先制作了一批5~20 mm和5~30 mm两种连续级配的C40,C55和C70碎石混凝土棱柱体试件,采用425#硅酸盐水泥、湘江河砂和长沙县莲花桥碎石场的玄武岩碎石,配合比分别为:水∶水泥∶砂∶碎石=0.420∶1∶1.186∶2.304,0.405∶1∶1.849∶2.555和0.360∶1∶1.458∶2.520。在不同测试龄期,用各强度等级和级配相同的混凝土分别制作6个150 mm×150 mm×300 mm标准混凝土棱柱体试件和1个200 mm×200 mm×500 mm大尺寸混凝土棱柱体试件。其次制作了4片2.2 m长的C50钢筋混凝土矩形构件,编号分别为L-A,L-B,L-C和L-D。各片构件的计算跨径为2.0 m,横截面尺寸为b×h=100 mm×180 mm,下缘配置2根直径为12 mm的HRB335纵向钢筋,上缘配置2根直径为4 mm的R235架立钢筋,箍筋采用直径为4 mm的R235钢筋,见图1。采用525#普通硅酸盐水泥,L-A和L-C构件的骨料采用5~20 mm连续级配碎石;L-B和L-D构件的骨料采用5~30 mm连续级配碎石。配合比均为:水∶水泥∶砂∶碎石=0.505∶1∶1.272∶2.554。同时,按照相同的配合比,分别制作了一批5~20 mm 和5~30 mm两种连续级配粒径的150 mm×150 mm×300 mm 素混凝土棱柱体试件。混凝土试件及钢筋混凝土构件都置于暴露试验站中自然养护,见图2。
|
| 图 1 钢筋混凝土矩形构件的尺寸及配筋(单位:mm) Fig. 1 Dimensions and bars of reinforced concrete rectangular members(unit:mm) |
| |

|
| 图 2 混凝土试件及构件自然养护 Fig. 2 Curing of concrete specimens and members in natural environment |
| |
2 混凝土试件长期弹性模量试验研究 2.1 超声测试混凝土动弹性模量的依据
根据国内外科学研究,超声波声速不可避免地受到混凝土材料组分与结构状况差异等综合因素的影响[15]。混凝土的动弹性模量Ed与泊松比μ等参数之间存在以下关系:
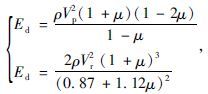
|
(1) |
式中,ρ为混凝土的密度;Vp,Vr分别为超声波在混凝土中传播的纵波速度和表面波速度。
把式(1)进行转换,可得:
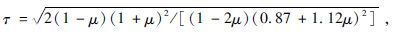
|
(2) |
式中,τ为纵波波速Vp与表面波波速Vr的比值。
据式(1)和式(2)可知,只需在混凝土表面获得超声波传播的Vp和Vr,或者两者的比值τ,即可求解混凝土的动弹性模量Ed及泊松比μ。
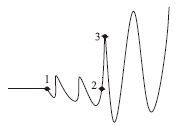
将RS-ST01C非金属超声检测仪的一对纵波收、发换能器以一定间距置于混凝土表面,进行超声波平测法测试,可获得如图3所示的波形[16]。因纵波的波速最大及对应的振幅很小,波形的前部分为纵波,且特征点1为纵波的初至点,而表面波的信号强及能量大,随着表面波的到达,波形的振幅会随之突然增大,特征点2和3分别为表面波的到达点和第一个峰值点。
|
| 图 3 超声波平测法波形及特征点 Fig. 3 Waveform and characteristic points of ultrasonic method |
| |
为了消除仪器读数并减少固体材料不均匀性的影响,在混凝土表面,采用多点平测法分别测试50,100,150,200,250,300 mm等6个不同测距的声时值。测试的可能波形特征点如图4所示,根据各测距下所测试的声时数据,绘制A,B,C,D各特征点的测距-声时散点图,用不同测距-声时散点的回归计算方程式,可获得Vp,Vr的大小。
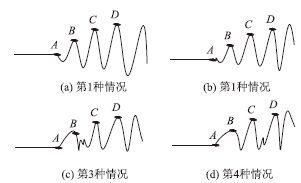
|
| 图 4 超声波平测法可能的波形特征点 Fig. 4 Possible characteristic points of ultrasonic plane testing method |
| |
2.2 混凝土试件长期动静弹性模量试验
(1) 静弹性模量试验结果
在不同测试龄期,相同粒径和相同强度等级的标准混凝土棱柱体试件各取6个,进行静弹性模量测试[17]。碎石混凝土试件的静弹性模量Es试验结果见表1。
| 粒径/mm | 测试龄期/d | C40 | C55 | C70 |
| 5~20 | 28 | 33.27 | 36.80 | 38.80 |
| 90 | 35.08 | 38.67 | 40.88 | |
| 180 | 35.70 | 39.57 | 41.69 | |
| 790 | 36.62 | 40.53 | 42.71 | |
| 5~30 | 28 | 35.47 | 37.62 | 38.52 |
| 90 | 37.39 | 39.63 | 40.57 | |
| 180 | 38.14 | 40.42 | 41.36 | |
| 790 | 39.05 | 41.41 | 42.39 |
(2) 动弹性模量试验结果
在各测试龄期,采用RS-ST01C非金属超声检测仪测试200 mm×200 mm×500 mm大尺寸混凝土棱柱体试件的Vp和Vr,并采用电子称对其称重,得到密度ρ。以下只列举了28 d龄期的碎石混凝土试件的测距与声时之间关系和ρ,Vp,Vr的试验结果。
1) 密度试验结果
28 d龄期的各大尺寸碎石混凝土棱柱体试件的密度试验结果见表2。
| 5~20 mm粒径 | 5~30 mm粒径 | ||||
| C40 | C55 | C70 | C40 | C55 | C70 |
| 2 387 | 2 429 | 2 466 | 2 432 | 2 473 | 2 487 |
2) 波速试验结果
28 d龄期的大尺寸碎石混凝土棱柱体试件的测距-声时散点图见图5。
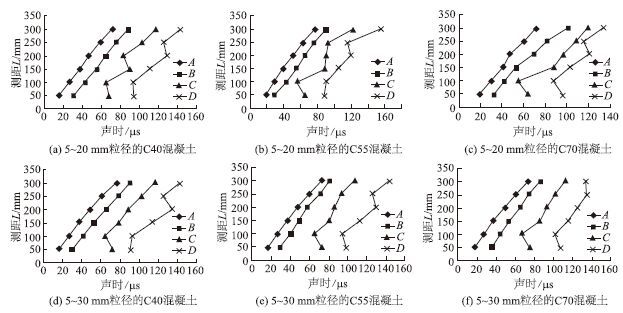
|
| 图 5 28 d龄期的碎石混凝土试件的测距-声时散点图 Fig. 5 Range-sound diagram of gravel concrete specimens at 28 d age |
| |
在图5(a)中,A特征点的各散点相连,几乎为一条直线。运用最小二乘法,进行直线(方程L=a+bt)回归,该直线方程的斜率即为纵波声速Vp。而由于表面波的滞后到达,波形的振幅会突然增大,在B~C特征点、C~D特征点之间产生了畸变,从而导致C,D两特征点的各散点连线为曲线。生成的畸变分支波在以后的各测距中会逐渐变大,并逐步成为独立的波峰,就成为一个新的波峰读数测点。试用一根直线去串联相关测点,如串联图5(a)中的C特征点的第1点与D特征点的第2~4点,将这些被连接测点的测距和声时数据以最小二乘法回归成直线方程L=a+b′t后,方程的斜率即为疑似表面波传播速度Vr[16]。以相同的方式可获得其他粒径和强度等级下的波速结果,28 d龄期的碎石混凝土试件的Vp和Vr试验结果见表3。
| 粒径/mm | 项目 | C40 | C55 | C70 |
| 5~20 | Vp /(m·s-1) | 4 559 | 4 623 | 4 833 |
| Vr /(m·s-1) | 2 261 | 2 366 | 2 433 | |
| 5~30 | Vp /(m·s-1) | 4 733 | 4 826 | 4 899 |
| Vr /(m·s-1) | 2 418 | 2 437 | 2 439 |
根据上述试验结果,结合式(1)和式(2),可计算28 d龄期的碎石混凝土试件的动弹性模量Ed,同理可得其他龄期的试验结果,碎石混凝土试件的长期动弹性模量Ed的试验结果见表4和图6。
| 粒径/mm | 测试龄期/d | C40 | C55 | C70 |
| 5~20 | 28 | 36.89 | 40.39 | 43.92 |
| 90 | 38.91 | 43.11 | 45.50 | |
| 180 | 39.81 | 43.76 | 45.85 | |
| 790 | 40.53 | 45.11 | 47.33 | |
| 5~30 | 28 | 42.59 | 43.75 | 44.59 |
| 90 | 43.64 | 46.28 | 47.35 | |
| 180 | 44.60 | 46.57 | 48.20 | |
| 790 | 45.53 | 48.13 | 49.38 |
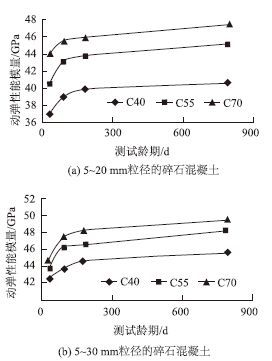
|
| 图 6 碎石混凝土试件的长期动弹性模量曲线 Fig. 6 Curves of long-term dynamic elastic modulus of gravel concrete specimens |
| |
碎石混凝土试件的动弹性模量随着时间的增长逐渐增大,且在前期增长迅速,后期增长缓慢,增长速率随时间增长而逐渐减缓。
2.3 混凝土试件长期动静弹性模量相关性研究基于最小二乘法,将各强度等级的碎石混凝土试件的静、动弹性模量试验值进行曲线拟合,见图7。拟合曲线的最小相关系数为0.957 5,回归精度较高。
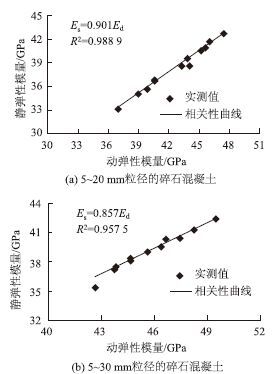
|
| 图 7 碎石混凝土试件的静-动弹性模量相关性曲线 Fig. 7 Curves of relativity of static-dynamic elastic moduli of gravel concrete specimens |
| |
碎石混凝土试件的静、动弹性模量之间存在以下的换算关系:
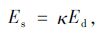
|
(3) |
式中,κ为换算系数。当粒径为5~20 mm时,κ=0.901;当粒径为5~30 mm时,κ=0.857。
3 钢筋混凝土构件长期弹性模量试验研究(1) 静弹性模量试验结果
在不同测试龄期,取与钢筋混凝土构件相同配比的标准混凝土棱柱体试件各6个,进行静弹性模量测试,试验结果作为相应龄期的钢筋混凝土构件的静弹性模量。钢筋混凝土构件的静弹性模量Es试验结果见表5。
| 粒径/mm | 测试龄期/d | |||
| 28 | 90 | 180 | 790 | |
| 5-20 | 35.49 | 37.19 | 38.23 | 38.85 |
| 5-30 | 36.67 | 38.47 | 39.29 | 39.73 |
(2) 动弹性模量试验结果
在各测试龄期,采用RS-ST01C非金属超声检测仪测试L-A和L-B构件的Vp和Vr,并采用电子称对相同龄期的L-C和L-D构件进行称重,得到密度ρ。以下只列举了28 d龄期的L-A或L-B构件的测距与声时之间关系和Vp,Vr,以及相同龄期ρ的试验结果。
1) 密度试验结果
28 d龄期的L-C和L-D构件的密度大小分别为2 595 kg/m3和2 623 kg/m3。
2) 波速试验结果
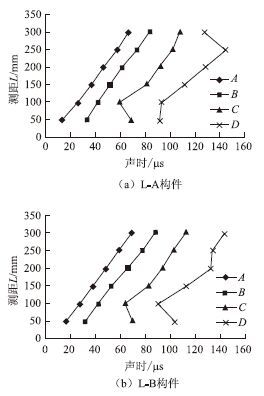
28 d龄期的L-A和L-B构件的测距-声时散点图见图8。
|
| 图 8 28 d龄期的钢筋混凝土构件的测距-声时散点图 Fig. 8 Range-sound diagram of reinforced concrete members at 28 d age |
| |
根据钢筋混凝土构件的测距-声时散点图,可获得28 d龄期的L-A和L-B构件的Vp和Vr,见表6。
| 编号 | 粒径/mm | Vp /(m·s-1) | Vr /(m·s-1) |
| L-A | 5-20 | 4 532 | 2 237 |
| L-B | 5-30 | 4 697 | 2 332 |
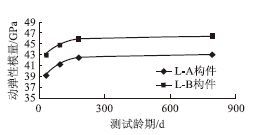
根据上述试验结果,结合式(1)和式(2),可计算28 d龄期的L-A和L-B构件的动弹性模量Ed,同理可得其他龄期的试验结果,L-A和L-B构件的长期动弹性模量Ed的试验结果见表7和图9。
| 梁号 | 粒径大小/mm | 测试龄期/d | |||
| 28 | 90 | 180 | 790 | ||
| L-A | 5-20 | 39.29 | 39.29 | 41.19 | 42.48 |
| L-B | 5-30 | 43.07 | 43.07 | 44.80 | 45.92 |
|
| 图 9 L-A和L-B构件的长期动弹性模量曲线 Fig. 9 Curves of long-term dynamic elastic modulus of L-A and L-B members |
| |
L-A和L-B构件的动弹性模量随时间变化律与混凝土试件的变化规律相同,前期增长迅速,后期增长缓慢,增长速率随时间增长而逐渐减缓。
(3) 长期弹性模量误差分析
根据式(3)和表7,可计算出L-A和L-B构件的换算静弹性模量Esh,将其与表5的实测静弹性模量Es进行比较,见表8。
| 编号 | 测试龄期/d | |||||||||||
| 28 | 90 | 180 | 790 | |||||||||
| Es/GPa | Esh/GPa | 误差/% | Es/GPa | Esh/GPa | 误差/% | Es/GPa | Esh/GPa | 误差/% | Es/GPa | Esh/GPa | 误差/% | |
| L-A | 35.49 | 35.40 | 0.25 | 37.19 | 37.11 | 0.22 | 38.23 | 38.27 | 0.10 | 38.85 | 38.79 | 0.15 |
| L-B | 36.67 | 36.91 | 0.65 | 38.47 | 38.39 | 0.21 | 39.29 | 39.35 | 0.15 | 39.73 | 39.70 | 0.08 |
| 注:误差=|Es-Esh|/Es×100%。 | ||||||||||||
L-A和L-B构件的长期换算静弹性模量的最大误差分别为0.25%和0.65%,误差较小。结果表明用式(3)进行5~20 mm和5~30 mm两种连续级配碎石混凝土构件的长期静、动弹性模量换算时,精度较高。
4 结论(1) 在进行桥梁混凝土长期弹性模量测试时,为弥补传统方法的不足,采用了超声波平测法测试桥梁混凝土在不同测距下的纵波波速及表面波波速,据此计算出混凝土的动弹性模量。
(2) 基于一批暴露试验的5~20 mm和5~30 mm 两种连续级配的碎石混凝土试件,开展了混凝土试件的长期静、动弹性模量试验研究。混凝土的动弹性模量随着时间的增长而逐渐增大,前期增长迅速,后期增长缓慢,增长速率随时间增长而逐渐减缓。
(3) 骨料的粒径大小会影响声波在混凝土中传播的速度,基于混凝土试件的长期静、动弹性模量试验研究成果,构建了5~20 mm和5~30 mm两种连续级配碎石混凝土试件的静、动弹性模量换算公式。
(4) 对自然暴露环境下的钢筋混凝土构件的长期静、动弹性模量进行了试验研究。将混凝土试件的静、动弹性模量换算公式应用于钢筋混凝土构件的长期静、动弹性模量计算时,精度较高。
| [1] | 彭晖, 张建仁, 郝海霞, 等. 锈蚀光圆钢筋混凝土受弯构件受力性能试验研究[J]. 公路交通科技,2015,32 (1) :83–89. PENG Hui, ZHANG Jian-ren, HAO Hai-xia, et al. Experimental Research on Mechanical Behavior of RC Flexural Members with Corroded Plain Steel Bars[J]. Journal of Highway and Transportation Research and Development, 2015, 32 (1) : 83–89 . |
| [2] | 孙晓燕, 董伟伟, 王海龙, 等. 侵蚀性环境下桥梁CFRP/BFRP加固后的长期性能试验[J]. 中国公路学报,2013,26 (2) :77–84. SUN Xiao-yan, DONG Wei-wei, WANG Hai-long, et al. Experiment for Long-term Performance of Bridge Girders Strengthened with CFRP/BFRP Sheets and Subjected to Erosion Environment[J]. China Journal of Highway and Transport, 2013, 26 (2) : 77–84 . |
| [3] | 唐国斌, 王统宁, 项贻强. 混凝土桥梁服役过程中荷载与锈蚀的耦合作用[J]. 公路交通科技,2013,30 (11) :62–67. TANG Guo-bin, WANG Tong-ning, XIANG Yi-qiang. Couple Effect of Loading and Corrosion of Concrete Bridge in Service Life[J]. Journal of Highway and Transportation Research and Development, 2013, 30 (11) : 62–67 . |
| [4] | 杨成学, 杨文礼, 杨露. 现场测试混凝土弹性模量的方法研究[J]. 四川理工学院学报:自然科学版,2010,23 (5) :504–507. YANG Cheng-xue, YANG Wen-li, YANG Lu. Field Testing Method for Elastic Modulus of Concrete[J]. Journal of Sichuan University of Science & Engineering:Natural Science Edition, 2010, 23 (5) : 504–507 . |
| [5] | SAWPAN M A, MAMUN A A, HOLDSWORTH P G, et al. Quasi-static and Dynamic Mechanical Elastic Moduli of Alkaline Aged Pultruded Fibre Reinforced Polymer Composite Rebar[J]. Materials and Design, 2013, (46) : 277–284 . |
| [6] | 蒋敏强, 陈建康, 杨鼎宜. 硫酸盐侵蚀水泥砂浆动弹性模量的超声检测[J]. 硅酸盐学报,2005,33 (1) :126–132. JIANG Min-qiang, CHEN Jian-kang, YANG Ding-yi. Dynamic Modulus of Cement Mortar in Sulphate Erosion Measured by Ultrasonic Checking[J]. Journal of the Chinese Ceramic Society, 2005, 33 (1) : 126–132 . |
| [7] | 屈锋, 牛荻涛, 杨宇曦. 盐冻循环作用下粉煤灰混凝土性能试验研究[J]. 工业建筑,2014,44 (6) :77–80. QU Feng, NIU Di-tao, YANG Yu-xi. Experimental Study of Performance of Fly Ash Fiber Concrete under the Action of Salt Frost[J]. Industrial Construction, 2014, 44 (6) : 77–80 . |
| [8] | HAN S H, KIM J K. Effect of Temperature and Age on the Relationship between Dynamic and Static Elastic Modulus of Concrete[J]. Cement and Concrete Research, 2004, 34 (7) : 1219–1227 . |
| [9] | 施士昇. 混凝土的抗剪强度、剪切模量和弹性模量[J]. 土木工程学报,1999,32 (2) :47–52. SHI Shi-sheng. Shear Strength, Modulus of Rigidity and Young's Modulus of Concrete[J]. China Civil Engineering Journal, 1999, 32 (2) : 47–52 . |
| [10] | 郑永来, 周澄, 黄炜, 等. 动态弹性模量的实验研究[J]. 河海大学学报,1998,26 (2) :31–35. ZHENG Yong-lai, ZHOU Cheng, HUANG Wei, et al. Experimental Study on Dynamic Elastic Modulus[J]. Journal of Hohai University, 1998, 26 (2) : 31–35 . |
| [11] | 郑永来, 周澄, 黄炜, 等. 动态弹性模量随频率变化的理论模型及机理[J]. 河海大学学报,1999,27 (3) :84–86. ZHENG Yong-lai, ZHOU Cheng, HUANG Wei, et al. Theoretical Model and Mechanism of Dynamic Modulus of Elasticity with Frequency Change[J]. Journal of Hohai University, 1999, 27 (3) : 84–86 . |
| [12] | 刘宏伟, 谢丽, 吴胜兴. 混凝土早龄期弹性模量无损检测初探[J]. 混凝土,2008, (6) :36–38. LIU Hong-wei, XIE Li, WU Sheng-xing. Tentative Research on Non-destructive Detection of Early-age Elastic Modulus of Concrete[J]. Concrete, 2008, (6) : 36–38 . |
| [13] | 张建仁, 唐腾, 彭晖, 等. 混凝土动、静弹性模量相关试验研究[J]. 中外公路,2010,30 (5) :256–260. ZHANG Jian-ren, TANG Teng, PENG Hui, et al. Experimental Research on Relevance between Static and Dynamic Elastic Moduli of Concrete[J]. Journal of China & Foreign Highway, 2010, 30 (5) : 256–260 . |
| [14] | 孙丛涛, 牛荻涛, 元成方, 等. 混凝土动弹性模量与超声声速及抗压强度的关系研究[J]. 混凝土,2010, (4) :14–16. SUN Cong-tao, NIU Di-tao, YUAN Cheng-fang, et al. Study on Relation between Dynamic Modulus of Elasticity and Velocity of Ultrasonic Sound and Compressive Strength for Concrete[J]. Concrete, 2010, (4) : 14–16 . |
| [15] | 李祝龙, 申爱琴, 李志波. 超声波在公路工程土工材料研究中的应用[J]. 公路交通科技,2000,17 (6) :30–33. LI Zhu-long, SHEN Ai-qin, LI Zhi-bo. Application of Ultrasonic Wave in Highway Engineering Material Study[J]. Journal of Highway and Transportation Research and Development, 2000, 17 (6) : 30–33 . |
| [16] | 尹健, 童寿兴. 用超声纵波换能器测量混凝土动弹模量[J]. 建筑材料学报,2006,9 (4) :404–407. YIN Jian, TONG Shou-xing. Determination of Dynamic Elastic Modulus of Concrete Using Ultrasonic P-Wave Transducer[J]. Journal of Building Materials, 2006, 9 (4) : 404–407 . |
| [17] | GB/T 50081-2002,普通混凝土力学性能试验方法标准[S]. GB/T 50081-2002,Standard for Test Method of Mechanical Properties on Ordinary Concrete[S]. |
 2016, Vol. 33
2016, Vol. 33
