公路交通科技  2016, Vol. 31 Issue (4): 149-152,158

扩展功能

文章信息

张禄, 纪威, 李文亮, 任春晓
ZHANG Lu, JI Wei, LI Wen-liang, REN Chun-xiao
汽车驱动桥半轴时变可靠性设计
Time-dependent Reliability Design of Vehicle Driving Axle
公路交通科技, 2016, Vol. 31 (4): 149-152,158
Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 149-152,158
10.3969/j.issn.1002-0268.2016.04.023

文章历史

收稿日期: 2014-11-26
引用本文 0
张禄, 纪威, 李文亮, 任春晓. 汽车驱动桥半轴时变可靠性设计[J]. 公路交通科技, 2016, Vol. 31 (4): 149-152,158.
ZHANG Lu, JI Wei, LI Wen-liang, REN Chun-xiao. Time-dependent Reliability Design of Vehicle Driving Axle[J]. Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 149-152,158.
汽车驱动桥半轴时变可靠性设计
张禄1,2 , 纪威1, 李文亮2,3, 任春晓2    
1. 中国农业大学 工学院, 北京 100083;
2. 交通运输部公路科学研究院 北京 100088;
3. 北京理工大学 机械与车辆工程学院, 北京 100081
收稿日期: 2014-11-26;
作者简介: 张禄(1987-),男,福建永泰人,博士.
摘要: 针对汽车驱动桥半轴的初始参数不确定性及其在使用过程不确定性的影响,研究在此条件下半轴可靠性设计的问题。推导了一种考虑初始参数不确定性的一维布朗微分方程,并构建了时变模型。结合应力-强度干涉理论,提出了一种考虑驱动桥半轴初始参数不确定条件下结构参数、载荷及强度随时间演变的可靠性设计方法。结果表明:不考虑驱动桥半轴初始参数不确定性与使用过程不确定性的可靠性设计偏向于不安全,采用本文方法计算得到驱动桥半轴直径的均值为64.78 mm时满足时变可靠性设计要求。
关键词: 汽车工程     时变可靠性设计     应力-强度干涉法     驱动桥半轴     初始参数不确定性     实际使用     一维布朗运动方程    
Time-dependent Reliability Design of Vehicle Driving Axle
ZHANG Lu1,2 , JI Wei1, LI Wen-liang2,3, REN Chun-xiao2    
1. School of Engineering, China Agriculture University, Beijing 100083, China;
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
3. School of Mechanical and Vehicular Engineering, Beijing Institute of Technology, Beijing 100081, China
Abstract: Aiming at the influence under uncertainties of initial parameters and actual use of vehicle driving axle, the reliability design of driving axle under this condition is discussed. A time-dependent model is established based on deriving the stochastic differential equation of 1D Brownian movement considering uncertainty of initial parameters. A time-dependent reliability design method considers dynamic evolution of structure parameters, load and strength under the uncertainty of initial parameters is established by stress-strength interference theory. The result shows that reliability design without consideringthe uncertainties of initial parameters and its actual use tend to be unsafe,while it can meet the time-dependent reliability requirements when the mean value of driving axle's diameter calculated by the presented method is 64.78 mm.
Key words: automobile engineering     time-dependent reliability design     stress-strength interference method     driving axle     uncertainty of initial parameter     actual use     1D Brownian movement equation    
0 引言

可靠性设计是保证机械产品及其零部件满足给定的可靠性指标的一种机械设计方法。汽车在工作时其零部件的可靠度随时间不断变化, 即时变可靠性, 其设计远比静态可靠性设计复杂得多, 是实时反映汽车零部件的重要指标之一, 而越来越受到关注。

SALVATORE等[1, 2]针对动载荷对零部件的作用而进行的可靠性分析, 但没有考虑强度和载荷与时间的关系。石博强等[3, 4]研究了初始结构参数及强度确定的机械零部件在使用过程中结构参数、强度及载荷受到不确定因素影响的时变可靠性。王新刚等[5]建立了变幅随机载荷和强度退化下的机械零部件动态可靠性模型。ANDRIEU-RENAUD等[6]基于体系可靠性分析技术提出了一种求解时变可靠性的高效方法。DER KIUREGHIAN等[7, 8]对非线性动态可靠性问题进行了研究。Shinozuka[9]给出了在时间区间内可靠度上下界的计算公式。Savage等[10, 11, 12, 13]把时变可靠性优化设计运用到产品寿命周期设计中。王正等[14, 15]运用泊松随机过程描述载荷的作用过程, 分别建立强度不退化和强度退化时的零件动态可靠性模型。黄新萍等[16, 17]针对时变结构可靠度分析方法开展了研究。龙进[18]分析转向机构的时变可靠性与综合设计。孙鸿宾等[19]提出一种基于动态Bayes网络的结构时变可靠性分析模型。石少卿[20]建立了基于马尔可夫链系统的时变可靠性分析方法。

本文主要基于文献[4]作进一步讨论, 将初始结构参数及强度的不确定与一维布朗运动随机微分方程相结合构建了时变模型, 并结合应力-强度干涉理论, 建立考虑汽车驱动桥半轴初始结构参数不确定条件下载荷和结构参数的时变设计数学模型。提出了一种考虑驱动桥半轴初始参数不确定性与使用过程中随时间变化的时变可靠性设计方法。

1 时变计算模型

汽车零部件的特性参数随时间而逐渐变化, 例如疲劳导致强度退化、磨损导致尺寸减小、工况恶劣导致载荷增大等, 因此必须将其处理为随机过程。

设(Ω,F,P)是一个概率空间, Ω为概率空间中的非空集合, F为Ω上的σ代数, P为Ω上的一个概率测度。假如, 随机变量X满足：

式中, t为时间变量；{B(t),t≥0}为一维标准布朗运动；λ和δ为常系数。

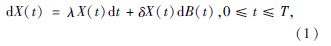
实际中在时间历程下载荷s、结构参数x及强度r受到确定性和不确定性因素共同作用, 三者的耦合效应为概率演化模式[4], 其方程为：

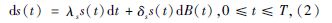
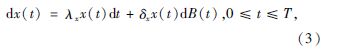
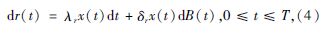
式中, λs, λx及λr分别为载荷、结构参数及强度的漂移率, 为确定性因素产生的变化效应；δs, δx及δr分别为载荷、结构参数及强度的波动率, 为不确定性因素产生的随机波动。其中漂移率和波动率均与时间无关。

同时, ln[s(t)], ln[x(t)]及ln[r(t)]服从正太分布[3], 即

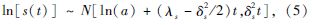
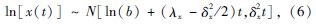
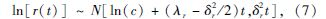
式中, a=s(0),b=x(0),c=r(0), 其中波动率和漂移率基于实际测试得到, 具体计算可参考文献[3]。

由于驱动桥半轴初始结构参数b与初始强度c存在不确定性, 假设二者相互独立, 并且b与c的概率分布函数为F1(b)与F2(c), 则在时变条件下ln[x(t)]的分布是由不同的b时变后的分布加权而得, 其中b对应的权重为概率分布F1(b), 得ln[x(t)]=F1(b)×N[ln(b)+(λx－12δ2x)t,δ2xt], 假设结构参数的波动率和漂移率为独立变量, 因此时变条件下结构参数的对数ln[x(t)]时变分布为：

即
同理, 可得考虑初始强度不确定性条件下强度的对数ln[r(t)]时变分布为：

2 时变可靠性模型

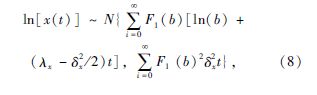
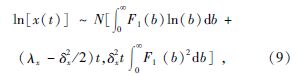
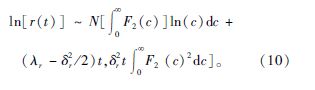
根据应力-强度干涉理论, 令时变条件下汽车零部件可靠性的状态方程为：

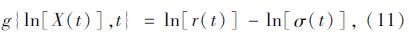
式中, ln[X(t)]为基本随机参数矢量的对数, g{ln[X(t)],t}服从正太分布N[μln(r)(t)－μln(σ)(t),σln(r)(t)2+σln(σ)(t)2], 因此零部件的可靠度为R(t)=P(g{ln[X(t)],t}>0)。

可靠性指标为：

则可靠度为：
3 驱动桥半轴可靠性设计 (1)已知条件

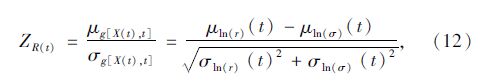
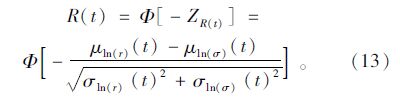
驱动桥半轴材料为45#钢, 其扭转剪切应力计算公式为：

式中, Tb为驱动桥半轴所受到的转矩;D为驱动桥半轴直径。

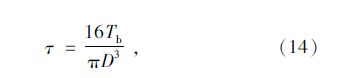
已知实测初始值为1.7×104N·m, 转矩时变的漂移率为λT=10－4, 波动率为δT=8×10-3；由于制造工艺的差异性, 假设驱动桥半轴直径D(0)服从：D(0)～N[D0,(D0v)2], 其中变异系数v为0.005, 直径时变的漂移率为λD=-2×10－5, 波动率为δD=2×10-3；扭转破坏试验得到驱动桥半轴的初始抗扭强度服从c～N(600,152), 其漂移率为λr=-1.8×10－4, 波动率为δr=3×10-3。要求该类汽车工作1年后驱动桥半轴的可靠度不低于0.995。以上主要数据来自于参考文献[3, 4]。

驱动桥半轴的应力主要取决于载荷与结构参数, 对式(14)两边取对数ln(τ)=ln(16/π)+ln(Tb)－3ln(D), 由于驱动桥半轴初始参数D(0)的不确定性, 时变条件下驱动桥半轴直径的对数ln[D(t)]分布函数为：

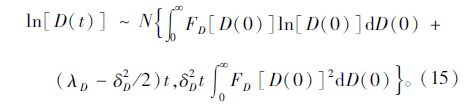
时变条件下应力的对数ln[τ(t)]均值和方差分别为：

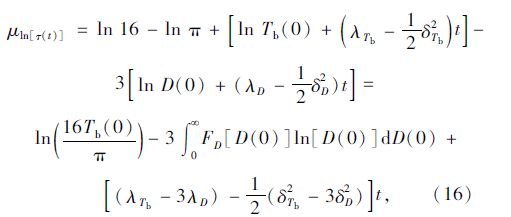
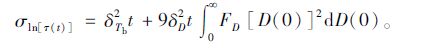
由式(15)可知, 驱动桥半轴受到应力的分散性除了与初始载荷、时变的载荷波动率有关, 还与驱动桥半轴初始直径的分散性及时变的波动率有关。结合式(10)、(12)及式(13)可求得驱动桥半轴的时变可靠性指标为：

(2)结果

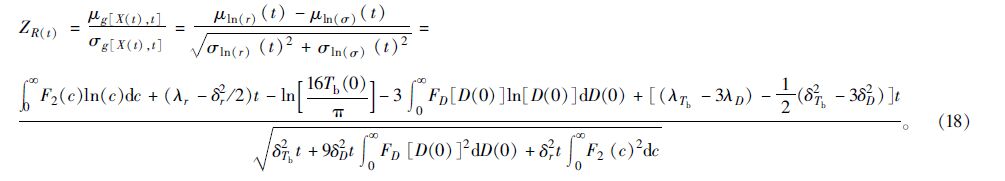
根据设计要求, 该类汽车工作1年后驱动桥半轴的可靠度不低于0.995, 即可靠性指标Z不低于2.575。

采用牛顿迭代算法, 迭代初始值可设置为：

D0=316Tbπμ(c), 迭代函数f=ZR(t)[D(0),v]－2.575。

计算得到满足可靠性设计要求的驱动桥半轴直径的变异系数为0.005时, 直径的均值μD(0)=64.87, 方差σD(0)=0.322。与文献[4]进行对比, 其未考虑驱动桥半轴初始结构参数的分散性, 得到驱动桥半轴直径的均值为60.24 mm, 低于本文考虑驱动桥半轴初始结构参数不确定性的计算结果。因此, 不考虑初始参数不确定性与使用过程不确定性的可靠性设计偏向于不安全。

4 结论

针对汽车驱动桥半轴的设计, 从其实际工况和载荷实际作用效果出发, 推导了一种考虑初始不确定性基于一维布朗运动随机微分方程的时变模型, 提出了一种驱动桥半轴时变可靠性设计方法。该方法不仅考虑了驱动桥半轴初始结构参数及强度的不确定性, 也考虑了结构参数、强度退化及工作应力变化的动态演化, 对驱动桥半轴时变可靠性的影响。结果分析表明, 不考虑初始参数不确定性及使用过程中随时间变化的可靠性设计偏向于不安全, 采用本文方法设计得到驱动桥半轴直径的均值为64.78 mm 时满足要求。该方法可为汽车零部件, 为实际使用时变可靠性设计提供了一种新思路。

参考文献
[1] BENFRATELLO S, CIRONE L, GIAMBANCO F. A Multicriterion Design of Steel Frames with Shakedown Constraints[J]. Computers and Structures, 2006,84(5):269-282.
[2] CHAUDHURI A, CHAKRABORTY S. Reliability Evaluations of 3-d Frame Subjected to Non-stationary Earthquake[J]. Journal of Sound and Vibration, 2003, 295(4):797-808.
[3] 石博强,唐歌腾. 井下车用零件多裂纹扩展的时变可靠性分析[J].东北大学学报:自然科学版,2014,35(1):97-100. SHI Bo-qiang, TANG Ge-teng. Time-dependent Reliability Analysis of Underground Vehicle's Parts Based on Multi-crack Propagation[J]. Journal of Northeastern University:Natural Science Edition,2014,35(1):97-100.
[4] 唐歌腾,石博强,赵志国,等.驱动桥半轴时变不确定性设计[J].北京理工大学学报,2011,31(7):785-789. TANG Ge-teng, SHI Bo-qiang, ZHAO Zhi-guo, et al. Driving Axle's Time-dependent Design Under Uncertainty[J]. Transactions of Beijing Institute of Technology,2011,31(7):785-789.
[5] 王新刚,张义民,王宝艳.机械零部件的动态可靠性分析[J].兵工学报,2009,30(11):1510-1514. WANG Xin-gang, ZHANG Yi-min, WANG Bao-yan. Dynamic Reliability Analysis of Mechanical Components[J]. Acta Armamentarii, 2009,30(11):1510-1514.
[6] ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M. The PHI2 Method:A Way to Compute Time-variant Reliability[J]. Reliability Engineering and System Safety, 2004, 84(1):75-86.
[7] DER KIUREGHIAN A. The Geometry of Random Vibrations and Solutions by Form and Sorm[J]. Probabilistic Engineering Mechanics, 2000, 15(1):81-90.
[8] DER K A, LI C C. Nonlinear Random Vibration Analysis Through Optimization[C]//Proceedings of the Seventh IFIP WG 7.5 Working Conference on Reliability and Optimization of Structural Systems. London:Pergamon Press, 1996:197-206.
[9] SHINOZUKA M. Probability of Structural Failure under Random Loading[J]. Journal of Engineering Mechanics Division,1964, 90(1):147-171.
[10] CAZUGUEL M, RENAUD C, COGNARD J Y. Time-variant Reliability of Nonlinear Structures: Application to a Representative Part of a Plate Floor[J]. Quality and Reliability Engineering International, 2006, 22(1): 101-118.
[11] SINGH A, MOURELATOS Z P, LI J. Design for Lifecycle Cost Using Time Dependent Reliability[J]. Journal of Mechanical Design, 2010, 132(9): 1-11.
[12] ROYSET J O, DER KIUREGHIAN A, POLAK E. Optimal Design with Probabilistic Objectives and Constraints[J]. Journal of Engineering Mechanics, 2006, 132(1): 110-118.
[13] SREICHER H, RACKWITZ R. Time-variant Reliability-oriented Structural Optimization and a Renewal Model for Life-cycle Costing[J]. Probabilistic Engineering Mechanics, 2004,19:171-183.
[14] 王正,谢里阳,李兵. 随机载荷作用下的零件动态可靠性模型[J]. 机械工程学报,2007,43(12):20-25. WANG Zheng, XIE Li-yang, LI Bing. Time-dependent Reliability Model of Component under Random Load[J]. Chinese Journal of Mechanical Engineering,2007,43(12):20-25.
[15] 王正,谢里阳.不确定性载荷作用下的零件时变可靠性模型[J].航空学报,2009,30(7):1243-1247. WANG Zheng,XIE Li-yang.Time-variant Reliability Model of Components Under Uncertain Loads[J].Acta Aeronautica et Astronautica Sinica,2009,30(7):1243-1247.
[16] 黄新萍,姜潮,韩旭. 针对非线性极限状态方程的时变可靠度分析[J].力学学报,2014,46(2):264-272. HUANG Xin-ping, JIANG Chao,HAN Xu. A Time-variant Reliability Analysis Method for Non-linear Limit-state Functions[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014,46(2):264-272.
[17] 姜潮,黄新萍,韩旭,等. 含区间不确定性的结构时变可靠度分析方法[J].机械工程学报,2013,49(10):186-193. JIANG Chao, HUANG Xin-ping, HAN Xu, et al. Time-dependent Structural Reliability Analysis Method with Interval Uncertainty[J]. Journal of Mechanical Engineering,2013,49(10):186-193.
[18] 龙进.转向机构的时变可靠性分析与综合[D].成都:西华大学,2012. LONG Jin. Analysis and Synthesis of Time-dependent Reliability of Steering Mechanisms[D]. Chengdu:Xihua University,2012.
[19] 孙鸿宾,吴子燕,刘书奎.基于动态Bayes网络的结构时变可靠性分析[J].应用数学和力学,2014,35(1):102-110. SUN Hong-bin, WU Zi-yan, LIU Shu-kui. A Dynamic Bayesian Network Model for Structural Time-dependent Reliability Analysis of Resistance Deterioration[J]. Applied Mathematics and Mechanics,2014,35(1):102-110.
[20] 石少卿,姜节胜. 基于马尔可夫链的系统时变可靠性分析[J]. 机械强度,1998,3(9):189-192. SHI Shao-qing,JIANG Jie-sheng. Time-Variant System Reliability Analysis Based on the Markov Chain[J]. Journal of Mechanical Strength,1998,3(9):189-192.