扩展功能
文章信息
- 黄粉莲, 纪威, 申立中
- HUANG Fen-lian, JI Wei, SHEN Li-zhong
- 基于行驶工况的货车动力传动系统优化
- Optimization of Truck Powertrain Based on Driving Condition
- 公路交通科技, 2016, Vol. 31 (4): 142-148
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 142-148
- 10.3969/j.issn.1002-0268.2016.04.022
-
文章历史
- 收稿日期: 2014-10-29
2. 中国农业大学 工学院, 北京 100083
2. School of Engineering, China Agricultural University, Beijing 100083, China
汽车动力传动系统参数及控制规律是影响汽车动力性、燃油经济性和排放性能最重要的因素,而行驶工况是汽车动力传动系统优化设计的参考依据[1, 2]。行驶工况是车辆实际道路行驶状况的反映,是考察某类车辆在某一特定地区的能源消耗量以及污染物排放的评价标准和检测依据[3]。行驶工况对营运货车的污染物排放和燃油经济性影响很大,完成不同循环时发动机的工作区域和工作状况不同,燃烧和做功效率不同,导致燃油消耗和污染物的生成有较大差异[4, 5]。基于行驶工况对动力传动系统进行优化设计,使车辆在实际运行过程中,较多地工作于高效率区,对改善动力传动系统的匹配、提高车辆的燃油经济性、控制污染物排放都具有重要意义[6, 7]。
1 行驶工况下车辆性能仿真分析 1.1 行驶工况国家标准GB 18352.5—2013《轻型汽车污染物排放限值及测量方法(中国第五阶段)》规定轻型柴油载货汽车排放测试必须在带有负荷和惯量模拟的底盘测功机上进行Ⅰ型试验(常温下冷起动后排气污染物排放试验)。试验共持续19分40秒,由两部分(1部和2部)组成。试验1部由4个城区循环组成,每个城区循环包含15个工况(怠速、加速、匀速、减速等);试验2部由1个城郊循环组成,该循环包含13个工况(怠速、加速、匀速、减速等)[8]。
1.2 仿真模型验证根据样本车辆(基本参数见表 1)发动机台架试验数据及车辆动力传动系统动力学关系[9],利用MATLAB平台建立货车动力传动系统仿真程序,在行驶工况下对车辆循环百公里燃油消耗、碳烟(PM)排放、氮氧化物(NOx)排放特性进行仿真,结果如图 1~3所示。
| 参数 | 数值 | 参数 | 数值 |
| 发动机额定功率/kW | 120 | 主减速器传动比 | 3.762 |
|
发动机额定转速/ (r·min-1) | 3600 | 车轮滚动半径/m | 0.388 |
| 空气阻力系数 | 0.465 | ||
| 发动机最大转矩/(N·m-1) | 360 | 迎风面积/m2 | 2.23 |
| 发动机BSFC/ [g·(kW·h-1)] | ≤205 | 最高车速/(km·h-1) | 150 |
| 整车起步加速时间/s | 14 | ||
| 汽车整备质量/kg | 1 860 | 最大爬坡度/% | ≥60 |
| 汽车总质量/kg | 2 885 | 综合燃油消耗[L·(100km)-1] | 8.1 |
| 6.495∶4.007∶ | [L·(100 km)-1] | ||
| 变速器传动比 | 2.316∶1.426∶ | ||
| 1:0.807 |
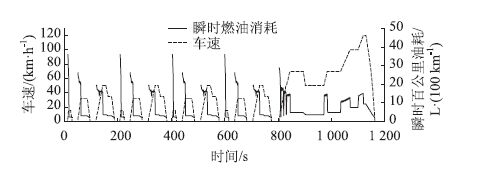
图 1为行驶工况下车辆循环百公里燃油消耗随车速变化的关系。由图可见,行驶工况变化对车辆循环百公里燃油消耗影响显著,每个循环车辆起步加速、急加速阶段瞬时百公里燃油消耗均很高,且波动范围较大,在低速加速区域达到峰值。车辆处于匀速行驶状态时,瞬时百公里燃油消耗量与车速呈正线性相关。整个循环的平均燃油消耗为8.004 L/(100 km),与试验结果的相对误差仅为1.23%
|
| 图 1 行驶工况下百公里油耗特性 Fig. 1 Fuel consumption per 100 km under driving condition |
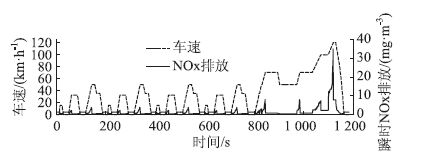
图 1为行驶工况下NOx瞬时质量排放浓度随车速变化的关系。由图可见:NOx瞬时质量排放浓度随工况变化关系明显,车辆怠速时排放浓度稳定;车辆加速时,NOx排放浓度显著增大;加速结束或车辆减速会导致NOx排放浓度迅速降低,并有较大幅度波动。车辆处于匀速行驶状态时,NOx排放量基本与车速成正比关系,这与文献[10, 11]中的研究结果一致。NOx排放随车速和加速度的增大而升高,城郊循环工况的车速高于城区循环工况车速,故城郊循环工况的NOx排放量明显高于城区循环工况,其峰值也更高。
|
| 图 2 行驶工况下瞬时NOx排放特性 Fig. 2 NOx instantaneous emission under driving |
|
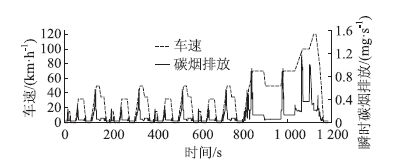
| 图 3 行驶工况下瞬时颗粒物排放特性 Fig. 3 PM instant emission under driving condition |
敏感性是指由于特定因素变动而引起的评价指标的变动幅度或极限变化[12]。为了研究主减速比及变速器各档传动比变化对车辆循环百公里燃油消耗、NOx排放、PM排放的影响程度。在车辆其余参数保持不变的情况下,分别将每个变量变化±10%后对模型进行仿真,单一变量相对敏感性按下式计算:
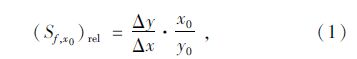
图 4为行驶工况下车辆百公里燃油消耗对主减速比与变速器各档传动比的相对敏感性。由图可见,百公里燃油消耗对传动比变化均不敏感,其中Ⅵ档传动比与主减速比对油耗的影响较大,Ⅵ档传动比增加10%,百公里油耗会增加1.17%;主减速比增加10%,则油耗增加0.89%。Ⅰ,Ⅱ,Ⅲ档传动比对百公里燃油消耗的敏感性系数较小,说明油耗对Ⅰ,Ⅱ,Ⅲ档传动比的变化均不敏感。Ⅳ,Ⅴ档传动比对百公里油耗的相对敏感性系数为负值,即其与百公里油耗的关系为负相关,Ⅳ,Ⅴ档传动比增加10%,则百公里燃油消耗分别降低0.14%,0.26%。

|
| 图 4 传动比对燃油消耗的相对敏感性 Fig. 4 Sensitivity of transmission ratio to fuel consumption |
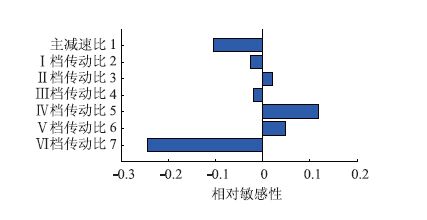
|
| 图 5 传动比对NOx排放的相对敏感性 Fig. 5 Sensitivity of transmission ratio to NOx emission |

|
| 图 6 传动比对颗粒物排放的相对敏感性 Fig. 6 Sensitivity of transmission ratio to PM emission |
在不改变整车主要配置的条件下,对传动系统的传动比进行优化设计是较为简单、可行的优化方案。本文以主减速比及变速器各档传动比为优化变量,行驶工况下百公里燃油消耗、PM排放及NOx排放量为优化目标,对传动系统进行多目标、多属性优化设计。样本车型配备的6 档自动变速器的Ⅴ档为直接档,其传动比为1,无需进行优化,则优化设计变量的矩阵为:
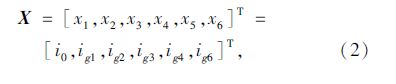
式中,i0为主减速比;igk为变速器第k档传动比。
3.2 优化目标函数对主减速比及变速器各档传动比进行优化设计的目标是从传动比分配组合的可行解集中求出最优解,优化问题可描述为:令Ω={X1,X2,…,Xn}为所有满足约束条件的传动比组合构成的解空间,F(Xj)为组合Xj对应的目标函数值,要求寻找最优解X*,使得对于所有的Xj=Ω,有F(X*)=minF(Xj)。
由于优化指标中行驶工况下百公里燃油消耗量、NOx排放及PM排放存在量纲、数量级不统一的问题,需将各分目标函数转化为无量纲、等量级的目标函数。
假设Qs(X)为传动比分配组合的可行解集Ω中任意传动比组合X对应的循环百公里燃油消耗量,存在最优解X^,使得对于所有的Xj=Ω,有Qs(X^)minQs(X)。则此时车辆的循环百公里燃油消耗量最小,即燃油经济性最佳。将Qs( X^)记为Qs,min,建立汽车循环百公里燃油消耗分目标函数表达式为:

由fQs(X)的定义可知,当车辆动力传动系统达到循环百公里燃油消耗最低的配置时,其百公里油耗等于汽车最佳燃油经济性时的油耗,即:Qs(X)=Qs,min,百公里燃油消耗分目标函数fQs(X)=1。其余情况下百公里燃油消耗油耗均大于最佳燃油经济性时的油耗,即Qs(X)>Qs,min、 fQs,则此时汽车的燃油经济性差一些。因此,FQs(X)值越小,且越接近于1,说明汽车的综合百公里燃油消耗越低、燃油经济性越好。
同理,对NOx排放和PM排放分目标进行归一化处理,得到NOx排放分目标函数:
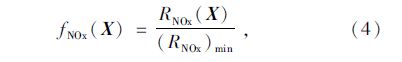
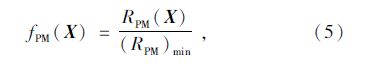
结合上述对经济性与排放性分目标函数的处理,将3个优化设计分目标函数按照其值的数量级和在整体设计中的重要程度相应地给出一组加权因子(权重系数)ωi,取fi(X)与ωj的线性组合,构成一个统一的目标函数F(X),即:
 式中,w1为经济性权重系数;w2为NOx排放权重系数;w3为PM排放权重系数。
式中,w1为经济性权重系数;w2为NOx排放权重系数;w3为PM排放权重系数。
在多属性决策分析中,通常采用权重来表示属性的相对重要性[13]。确定权重系数的方法很多,如主观赋权法、特征向量法、最小平方和法、熵值法、层次分析法、主成分分析法等[14],每种方法各有优缺点,需根据具体优化问题选用。本文优化指标关系复杂、指标之间的重要性难于科学定性,因此从各指标对目标模型的效应出发,根据变量对指标的敏感性分析结果确定各指标的权重系数。
敏感性系数的大小和符号反映变量变化对指标变化的影响程度和方向,敏感性系数为正表示设计变量与指标的关系为正相关,即设计变量增大指标也相应增大;敏感性系数为负则表示负相关,即设计变量增大,指标减小。敏感性系数绝对值越大的参数变化会造成指标越大幅度的变化,属于敏感变量,则目标变化时允许该参数变化的幅度要小[15]。对各参数允许升降幅度的分析,实质上是各变量对指标影响程度分析的反向推算,在计算上表现为敏感性系数绝对值的倒数[16]。
假设指标i(i=1,2,3分别对应Qs,NOx,PM)允许设计变量xk变化的幅度为:
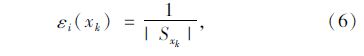
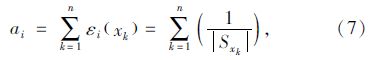
将ai归一化处理,可得权重系数:
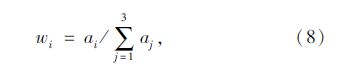
单个设计变量xk对指标的敏感性系数Sxk越大,则指标允许该设计变量变化的幅度越小。各设计变量对指标的综合效应值越大,则该指标在综合目标中的重要程度越大(例如:若X使百公里燃油消耗FQs(X)降低的程度越大,则fQs(X)对综合目标函数F(X)降低的贡献越大,则可对fQs(X)赋予较大权重)。
将各优化设计变量对指标的敏感性系数代入式(7)计算设计变量对各指标的效应值ai,再将结果代入式(8)计算可得各指标的权重系数如表 2所示。
| 指标 | 综合效应值 | 权重系数 |
| 百公里油耗 | a1=8.576 0 | w1=0.654 2 |
| NOx排放 | a2=4.081 6 | w2=0.311 4 |
| PM排放 | a3=0.451 1 | w3=0.034 4 |
在优化设计过程中,优化目标的实现通常受到实际情况或设计变量间的相互关系和取值边界限制,这种限值称为约束条件。本文的燃油经济性和排放性综合目标函数约束条件包括[9]:各档间速比的间隔要求、直接档最大动力因数约束、最大传动比要求、最大爬坡度的要求、道路附着条件、最高车速要求、发动机转速及转矩范围限制等。
3.5 优化计算本文研究的是一个具有6个设计变量,12个约束条件的最优化问题,其数学模型如下:
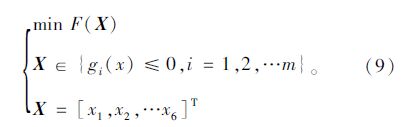
该模型是多属性非线性约束优化问题,优化的目标是求函数F(X)的最小值,且函数值越小,优化效果越好。根据优化模型的特点,本文选择信赖域算法[17,18]求解优化问题。
3.5.1 单目标优化基于上述优化变量、优化目标函数、指标权重及优化算法选择的理论分析与研究,利用Matlab编程对优化问题进行求解。首先对各评价指标进行单一目标优化,以确定指标的最优解及参数优化极限,优化结果如表 3所示。
由表 3可知,对车辆百公里燃油消耗进行单目标优化时,经济性权重系数w1=1,w2,w3=0。优化结果表明:在整车其余部件配置不变的条件下,通过调整传动系统传动比,该车型标准行驶工况下能达到的最低综合燃油消耗为Qs min7.8542L/(100 km)。同理,对 NOx与PM排放进行单目标优化,可得最低NOx排放(RNOx)min=0.360 8 g/km,最低PM排放(RPM)min=0.010 63 g/km。
| 目标及变量优化结果 | w1 w2 w3 | w1 w2 w3 | w1 w2 w3 |
| 1 0 0 | 0 1 0 | 0 0 1 | |
| 燃油消耗/[L·(100 km -1)] | 7.845 2 | 7.951 9 | 8.168 8 |
| NOx排放/(g·km-1) | 0.380 27 | 0.360 84 | 0.446 75 |
| PM排放/(g·km-1) | 0.011 21 | 0.011 650 | 0.010 629 |
| 最大爬坡度/% | 68.94 | 63.28 | 77.38 |
| 最高车速/(km·h-1) | 186.16 | 179.89 | 143.98 |
由单一目标优化确定Qs min,(RNOx)min,(RPM)min后,可知综合优化目标函数表达式为:
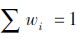
根据表 2中已确定的指标权重系数w1,w2,w3及选取的优化算法进行多次迭代即可求出使综合目标函数最小的百公里燃油消耗量Qs、NOx排放量RNOx及PM排放量RPM。利用Matlab编程求解上述优化问题,优化前后目标的对比如表 4所示。
| 指标 | 优化前 | 优化后 | 相对变化量/% |
| 燃油消耗/[L·(100 km -1)] | 8.004 | 7.995 | -0.112 4 |
| NOx排放/(g·km-1) | 0.378 1 | 0.377 5 | -0.158 7 |
| PM排放/(g·km-1) | 0.012 4 | 0.011 2 | -9.677 |
| 最大爬坡度/% | 71.03 | 73.10 | 2.916 |
| 最高车速/(km·h-1) | 168.97 | 167.64 | 0.79 |
由表 4可知,优化后综合百公里油耗降低0.1124%,NOx排放降低0.1587%,PM排放降低9.677%,百公里油耗与NOx排放略有改善,PM排放有较大幅度的降低。鉴于我国目前大范围内的雾霾重度污染,严格控制汽车PM排放以改善空气质量刻不容缓。该优化结果能在大幅降低PM排放的同时,对燃油经济性和NOx排放略有改善的,优化设计合理、可行。由于优化后主减速比有较大幅度增加(3.3%),最大传动比i0ig1及最小传动比i0ig6均增大,优化后车辆动力性有明显提高,最大爬坡度增加2.916%,最高车速降低0.79%,这对于提高货车动力性能具有重要现实意义。
4 结论本文通过研究车辆在标准行驶工况下的百公里燃油消耗、NOx和PM排放性能,分析传动系速比变化对目标的影响程度,提出一种基于敏感性分析结果确定指标权重系数的方法,以标准行驶工况下车辆最低燃油消耗、最低NOx和PM排放为目标,对传动系统主减速比、变速器各档传动比进行优化设计,确定了使目标较优的动力传动系统配置。主要结论如下:
(1)车辆综合百公里燃油消耗、NOx及PM排放对行驶工况的变化敏感影响显著,其值与车速、加速度密切相关。车辆加速、急加速阶段燃油消耗与污染物排放均急剧增加,且在加速区域达到峰值。
(2)百公里燃油消耗、NOx和PM排放,3个指标相互影响,彼此牵制,权重系数分配不同,优化结果差异很大。本文提出的优化方案能在3个优化指标中取得较好的折衷,优化后燃油消耗、NOx排放有所改善,PM排放则有较大幅度降低。
(3)不同货车消费者对车辆使用性能需求不同、且不同地区的排放法规要求各异,因此可根据专家经验或车辆具体性能要求,对各指标的权重系数进行调整,以满足车辆的多样化、个性化需求。
| [1] | BAGLIONE M L, DUTY M J. Development of Reverse Dynamic Optimization Methodology for Optimal Powertrain Integration and Control Design[C]//Proceedings of the ASME 2008 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Brooklyn: ASME, 2008: 1-10. |
| [2] | MARIA I. Fuel Optimal Powertrain Control for Heavy Trucks Utilizing Look Ahead[D]. Linköping:Linköpings University, 2009: 3-10. |
| [3] | 李忠剑,张俊智,卢青春,等. 运用特征参数对汽车驾驶循环的研究[J]. 汽车技术,2001(7):13-16. LI Zhong-jian, ZHANG Jun-zhi, LU qing-chun, et al. Study on Automotive Driving Cycle by Using Characteristic Parameters[J]. Automobile Technology,2001(7):13-16. |
| [4] | 孙宏图.基于循环工况的城市公交客车动力传动系统参数研究[D]. 大连:大连理工大学,2009:2-8. SUN Hong-tu. Study on Parameters of Power Train for Urban Bus Based on Driving Cycles[D]. Dalian: Dalian University of Technology, 2009: 2-8. |
| [5] | KULKARNI N C, JADHAV N, NANDKEOLYAR K. Drive Cycle for Commercial Vehicles for Selection of Power Train to get Optimum Fuel Efficiency[EB/OL].[2014-10-20].http://papers.sae.org/2009-01-2886. |
| [6] | BAGLIONE M L, DUTY M J. Reverse Dynamic Optimization of Variable Displacement Engine Operation and System Integration[C]//Proceedings of 2008 ASME Dynamic Systems and Control Conference. Ann Arbor: ASME, 2008: 1-8. |
| [7] | HUAJIE D, XIUMIN Y, JUNJIE L. et al. Study on Effects of Driving Style on Vehicle Performance for Econopower Competition[EB/OL].[2014-10-20].http://papers.sae.org/2008-01-1781. |
| [8] | GB 18352.5—2013,轻型汽车污染物排放限值及测量方法[S]. GB 18352.5—2013, Limits and Measurement Methods for Emissions from Light-duty Vehicles[S]. |
| [9] | 黄粉莲. 营运货车动力传动系统仿真优化[D]. 北京:中国农业大学,2014:98-100. HUANG Fen-lian. Simulation and Optimization of Commercial Truck Powertrain System[D]. Beijing:China Agricultural University, 2014:98-100. |
| [10] | 高继东,秦孔建,梁荣亮. 北京道路工况下公交车PM和NOx排放特性试验研究[J]. 汽车工程,2011,33(9):757-760. GAO Ji-dong, QIN Kong-jian, LIANG Rong-liang. An Experimental Study on the PM and NOx Emission Characteristics of Public Bus in Real Driving Condition in Beijing[J]. Automotive Engineering, 2011, 33(9): 757-760. |
| [11] | 陈晓明,宁智,宋云超,等. 重型柴油车道路循环工况下排放特性的仿真分析[J]. 环境科学学报,2012,32(1):109-115. CHEN Xiao-ming, NING Zhi, SONG Yun-chao, et al. Simulation on the Emission Characteristics of Heavy-duty Diesel Vehicle under Transient Driving Cycle[J]. Acta Scientiae Circumstantiae,2012,32(1):109-115. |
| [12] | 蒋艳,向学军,李宁. 多目标决策中的权重敏感性分析[J]. 三峡大学学报:自然科学版,2004,26(5):447-449. JIANG Yan, XIANG Xue-jun, LI Ning. Study on Weights Sensitivity of Multi-Objective Decision-making[J]. Journal of China Three Gorges University:Natural Sciences Edition,2004,26(5):447-449. |
| [13] | 杨保安,张科静. 多目标决策分析:理论、方法与应用研究[M]. 上海:东华大学出版社,2008:19-31. YANG Bao-an, ZHANG Ke-jing. Multi Objective Decision-making Analysis: Theory,Method and Application[M]. Shanghai:Donghua University Press,2008:19-31. |
| [14] | 王清. 多属性评价的权重敏感性度量及分析[D]. 武汉:华中科技大学,2006:8-14. WANG Qing. Weight Sensitivity Measurement and Analysis of Multi-criteria Evaluations[D].Wuhan: Huazhong University of Science and Technology, 2006:8-14. |
| [15] | 蒋艳, 陈荣秋. 基于权重最小变化量的参数敏感性分析[J]. 武汉理工大学学报,信息与管理工程版,2005,27(1):165-167. JIANG Yan, CHEN Rong-qiu. Parameter Sensitivity Analysis Based on the Least Variance of Weights[J]. Journal of Wuhan University of Technology: Information & Management Engineering Edition, 2005, 27(1): 165-167. |
| [16] | 蒋根谋,刘荣自. 基于敏感性分析的房地产风险投资多目标决策[J]. 商场现代化,2011,635(2):117-118. JIANG Gen-mou, LIU Rong-zi. Multi Objective Decision-making of Risk for Real Estate Investment Based on Sensitivity Analysis[J]. Market Modernization, 2011, 635(2):117-118. |
| [17] | 龚纯,王正林. 精通MATLAB最优化计算[M]. 北京:电子工业出版社,2012:94-206. GONG Chun, WANG Zheng-lin. Proficient in MATLAB Optimization Calculation[M]. Beijing: Publishing House of Electronics Industry, 2012:94-206. |
| [18] | 陈宝林. 最优化理论与算法[M]. 北京:清华大学出版社,2005:315-320. CHEN Bao-lin. Optimization Theory and Algorithm[M]. Beijing: Tsinghua University Press, 2005: 315-320. |
 2016, Vol. 31
2016, Vol. 31
