扩展功能
文章信息
- 王福建, 孙凌涛, 钱伟
- WANG Fu-jian, SUN Ling-tao, QIAN Wei
- 基于改进后冲击波剖面模型的宏观基本图特性研究
- Characteristics of Macroscopic Fundamental Diagram Based on SPM
- 公路交通科技, 2016, Vol. 31 (4): 127-133
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 127-133
- 10.3969/j.issn.1002-0268.2016.04.020
-
文章历史
- 收稿日期:2015-5-14
2. 杭州华龙交通勘察设计有限公司, 浙江 杭州 310058
2. Hangzhou Hualong Traffic Survey and Design Co., Ltd., Hangzhou Zhejiang 310058, China
随着社会经济的发展和人民生活水平的提高,逐渐增加的汽车使用量使得交通状态从交通拥挤不断向交通拥堵演化,使其成为亟待解决的关键问题之一。交通堵塞现象往往在某些敏感交叉口或路段反映出来,其原因就是在某一时段的大多数周期内,交通需求大于交通供给,导致车辆在绿灯时间内未能完全释放且不断累积,最终排队上溯导致上游交叉口发生堵塞,从而形成连锁反应,以致断面和基本路段的交通流特性无法适用。因此需要建立合适的能准确快速描述车辆排队现象的排队模型,并以此来研究路网的宏观交通流特性(即宏观基本图)。
1 研究现状 1.1 排队模型研究现状排队模型大致可分为3类:概率论方法[1, 2]、累积曲线法[3, 4]和冲击波法[5, 6, 7, 8, 9]。其中概率方法因为其无法满足任何一种概率分布的假设,无法适用于交通状态变化复杂的情况。当到达率和离开率变化复杂时,累积曲线法较难构建累计曲线,且存在一定的累计误差。因此本文选择在宏观上可以看做稳定流情形的、有较好描述效果的冲击波法进行研究。
在冲击波法应用于信号交叉口分析的研究中,Michalopoulos 等[5]将冲击波分析应用于信号交叉口,针对单个交叉口和交叉口群分别研究了具有排队长度约束的过饱和信号系统,特别关注了排队的动态变化和信号控制效果。Stephanopoulos 等[6]进一步运用冲击波方法探讨了信号交叉口交通排队动力学的建模和分析。隽志才等[7]以交通流流体力学理论为基础,采用准冲击波的方法对冲击波在交叉口的传递情况以及排队过程进行了模拟,并利用仿真结果计算得到了交叉口最大排队长度、最远排队点、交叉口平均受阻距离、停车率等指标。但以上方法都不适用于过饱和的情形。Wu等[8]基于冲击波理论,提出了一种基于段落的干线交通流动态性的建模方法,称为冲击波剖面模型,以拥有不变饱和流率的相同类型路段作为一个段落,追踪一个段落内或相邻两个段落内的主要冲击波,以此来描述交叉口动态排队过程,并用实际数据进行了验证。付凤杰等[9]应用冲击波法对信号交叉口排队长度最远点进行了分析研究,并建立了最大周期的优化模型。
1.2 宏观基本图研究现状Smeed[10]于1966年提出了能够进入城市中心区的车辆数是城市区域面积的函数,并与该城市的路网面积与道路可利用率相关。Herman[11]提出了二流模型,将路网上的车辆假设为自由流行驶和停止两种状态,得到单位距离车辆平均停车时间与平均行程时间的函数关系。在以上研究的基础上,Daganzo和Geroliminis[12, 13]得到了路网空间流量、密度等基本交通参数的固定关系,并将此定义为宏观基本图。此后,围绕宏观基本图的研究不断展开[14, 15, 16, 17],研究内容主要集中在其存在性、形状、影响因素及运用方向,且大多数研究都是基于Vissim仿真或以往的历史数据,Vissim仿真中参数标定的准确性直接影响结果的可靠性,而历史数据又存在一定的滞后性,因此本文旨在研究一种能快速准确得到宏观基本图的方法,为后续研究提供一定的理论基础[18, 19]。
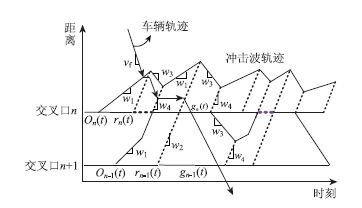
2 冲击波剖面模型介绍及改进冲击波剖面模型(Shockwave Profile Model,SPM)[8]是冲击波法在交叉口的具体应用,模型基于以下假设:(1)车辆在到达排队队尾前都以自由流速度行驶;(2)排队车辆以饱和流率释放;(3)消散冲击波波速已知。如图 1所示,该模型合理地将冲击波简化为红灯起亮初期形成排队的排队冲击波w1、绿灯起亮后形成的由停车线向后传播的消散冲击波w2、排队波和消散波相遇时形成的离去波w3和周期内有剩余排队形成的压缩波w4这4种主要的波,可方便地追踪信号交叉口间排队形成与消散的过程。
|
| 图 1 信号交叉口冲击波剖面图 Fig. 1 Profile of shockwave at signalized intersection |
SPM模型依据流量守恒定律和LWR模型中的波速公式,推导出4种冲击波的波速公式:
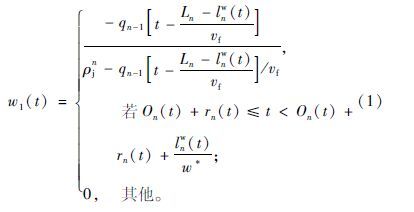
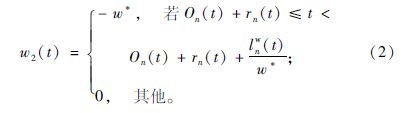
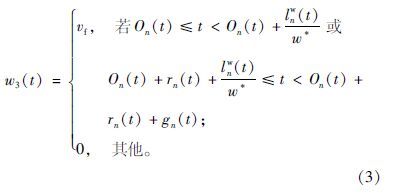
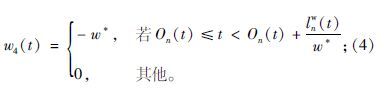
上述式中,Ln为交叉口n-1和交叉口n之间的路段长度; qn-1(t),lnw(t),vf,Sn,ρjn,ρsn,On(t),rn(t),gn(t)分别为路段Ln在t时刻的输入流率、排队长度、自由流速度、饱和流率、阻塞密度、饱和密度、所属周期的起始点、所属周期的红灯区间以及有效绿灯区间;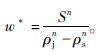
考虑在绿灯开始初期,车辆的释放流率会小于在自由流情况下最大的到达率,称之为通行能力下降,因此离去波波速w3(t)并非等于自由流速度,修正为如下公式:
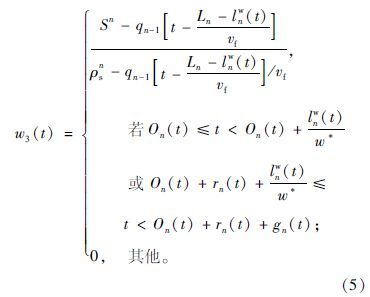
基于排队冲击波w1(t)和离去波w3(t)及当前排队长度lnw(t),可以更新下一个仿真时长(t+Δt)的排队长度lnw(t+Δt),其更新公式如下所示:
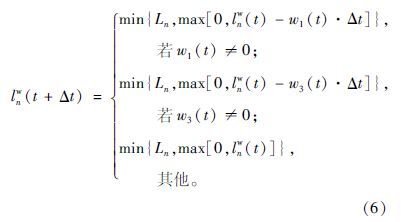
同理,基于排队冲击波w2(t)和压缩波w4(t)及当前存在波的波阵面的位置,可以更新下一个仿真时长(t+Δt)的波阵面位置lnw2(t+Δt)和lnw4(t+Δt),其更新公式如下:
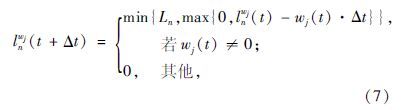
当冲击波位置得到更新后,就能构建冲击波模型,从而计算得到离开交叉口的流量,其结果如下:
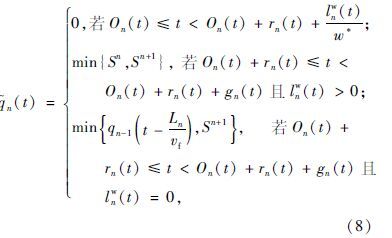
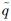 n(t)为交叉口n在t时刻的输出流率。
n(t)为交叉口n在t时刻的输出流率。
但对于无保护相位的信号交叉口来说,左转车流利用可接受间隙通过交叉口,因此其输出流量还受到冲突流可接受间隙的影响,引入参数γ(γ=0表示无可接受间隙来放行冲突车流;γ=1则相反)对式(8)进行如下修正:
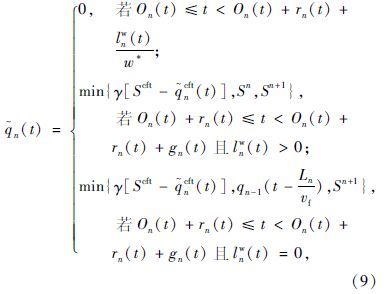
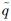 ncft(t)分别为存在冲突流时交叉口的饱和流率和离开流率。
ncft(t)分别为存在冲突流时交叉口的饱和流率和离开流率。
对于未保护相位交叉口,由于冲突流的存在,其实际饱和流率会小于理论饱和流率,因此需要修正,修正公式如下:
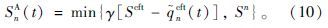
在得到上游交叉口的输出流率后,只要给出一个转弯比例就能知道下游交叉口直行的交通量,计算公如下:
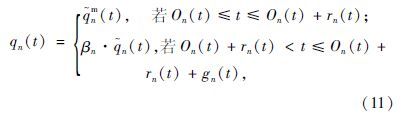
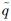 nm(t)是支路的离开率(包括左转和右转)。
nm(t)是支路的离开率(包括左转和右转)。
以上讨论的都是下游交叉口未溢出的情形,但现实中常常出现下游排队上溯的情形,因此还需对此情形进行讨论。由于溢出的不确定性和随机性(溢出何时发生、溢出状态持续的时间等)使情况变得相当复杂,但SPM模型能将其简单归纳成两种情况:
情况1:增加一个红灯相位,该情况适用于下游交叉口在上游交叉口是红灯时下游交叉口溢出且溢出状态持续到信号灯变绿;
情况2:创建一个新周期,其适用于上游交叉口是绿灯时下游交叉口溢出的情况。
由于排队溢出的情形能简单地被上述两种情况表示,因此对于排队溢出情形的处理就可以简化为在以下时段更新交叉口信号的时间:(1)下游交叉口排队上溯至上游交叉口;(2)下游交叉口的消散波传到上游交叉口。然而,SPM模型在每个时刻t内更新交通状态,当溢出发生时,无法知道溢出持续的时间。为了建模简便,将溢出发生时周期内剩余的时间作为红灯时间,将溢出消散时周期内剩余的时间作为绿灯时间,更新时间公式如下:
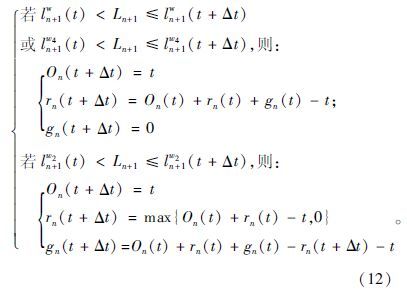
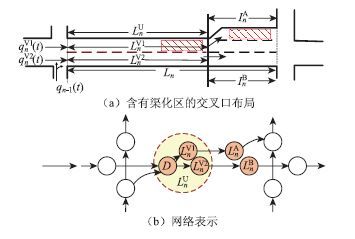
SPM模型采用基于段落的路网建模方法,把拥有不变饱和流率的相同类型路段归为一个段落,一个段落或两个相邻段落产生的主要冲击波会被明确地追踪。如图 2所示,以节点表示段落,以箭头表示方向,其中节点包括段落长度、阻塞密度、饱和流率、信号配时等大部分数据。
|
| LnU-路段未渠化段长度; LnA-左转渠化段长度; LnB-直行渠化段长度; LnV1-堵塞的车道长度;LnV2-未堵塞的车道长度;-虚拟节点。 图 2 含有渠化区的交叉口建模 Fig. 2 Modeling of an intersection with channelized area |
基于段落的建模方法是现实交通的近似模拟,因此假设车道事先已分配好,无换道行为,进入各路段的流量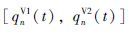 由转弯比例决定,其公式如下:
由转弯比例决定,其公式如下:
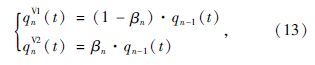
从式(13)可以看出,原模型将最内侧车道完全作为左转车辆的专用车道,这不仅大大降低了交叉口的通行能力,还与实际完全不符,因此需要对其进行改进。
2.3 模型的改进按实际情况常规设置,将最内侧车道作为直行车辆和左转车辆的共用车道,外侧车道作为直行车辆和右转车辆的共用车道,故其流量分配按下式进行改进
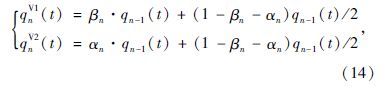
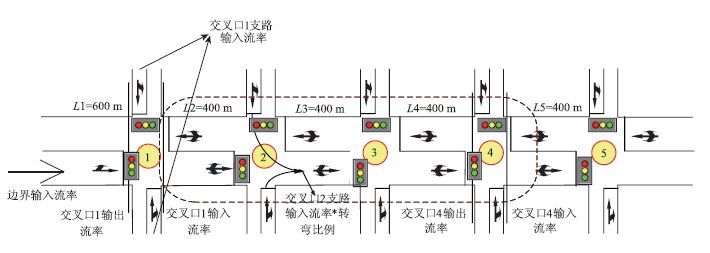
根据上一章的介绍和改进后的SPM算法,对其进行编程实现。以单车道干线5个交叉口为研究对象,路段长度均为300 m,研究对象如图 3所示。
|
| 图 3 试验对象的仿真设置 Fig. 3 Experimental object configuration for simulation |
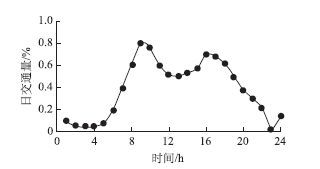
路段的自由流速度为36 km/h,饱和流率均为1 800 veh/h,饱和密度(临界密度)为65 veh/km,阻塞密度为130 veh/km,交叉口内的车辆初始排队数为0,在交叉口边界输入双峰流量,其中主路最大流量为1 000 veh/h,支路最大流量为600 veh/h,其双峰变化如图 4所示。
|
| 图 4 日交通量变化图 Fig. 4 Changes of daily traffic volume |
各交叉口均为两相位放行,周期为100 s,绿信比为0.55,交叉口3的相位差为10 s,交叉口4的相位差为20 s,其余交叉口无相位差。
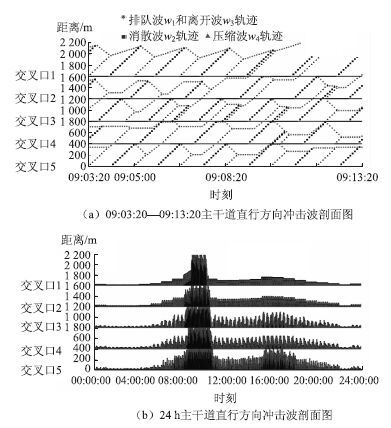
3.2 仿真结果及分析对1天24 h进行数值仿真,得到主干道各交叉口1天由左向右直行的冲击波图,结果如图 5所示。
|
| 图 5 主干道直行方向24 h冲击波剖面图 Fig. 5 Profiles of shockwave on arterial road in straight direction(24 hours) |
从图 5可以看出,在7:30以后各交叉口均出现拥挤现象。以交叉口5为例,8:00以后交叉口5出现排队上溯现象,影响交叉口4的车流运行,从而使整个交叉口都出现上溯,若为路网,则会出现锁死现象。
对路网进行1天24 h仿真,得到仿真时间段内每个仿真时刻进出各交叉口的车辆数,然后以5 min为时间间隔进行统计(部分数据如表 1所示),得到每个统计时间间隔内路段上的累计车辆数。为了防止无边界交叉口对结果造成影响,只取路段L2,L3,L4进行分析,计算每个时间段内的平均路网累积车辆数,然后根据各路段平均长度,得到路网加权平均密度。
| 时刻 | 5分钟序列 |
交叉口1 输入流量 |
交叉口2 输出流量 |
交叉口2 输入流量 |
交叉口3 输出流量 |
交叉口3 输入流量 |
交叉口4 输出流量 |
交叉口4 输入流量 |
交叉口5 输出流量 |
| 6:00—7:00 | 78 | 45.79 | 50.71 | 53.21 | 44.60 | 48.35 | 58.90 | 61.65 | 48.40 |
| 6:00—7:00 | 79 | 45.79 | 42.20 | 45.95 | 50.91 | 54.41 | 51.97 | 55.47 | 65.98 |
| 6:00—7:00 | 80 | 45.79 | 50.71 | 53.21 | 48.60 | 51.60 | 54.15 | 56.90 | 53.15 |
| 6:00—7:00 | 81 | 45.79 | 42.20 | 45.95 | 53.40 | 56.90 | 47.70 | 51.20 | 56.95 |
| 6:00—7:00 | 82 | 45.79 | 50.71 | 53.21 | 39.85 | 43.60 | 57.47 | 60.22 | 46.97 |
| 6:00—7:00 | 83 | 45.79 | 42.20 | 45.95 | 56.76 | 60.01 | 52.92 | 56.42 | 65.98 |
| 6:00—7:00 | 84 | 45.79 | 50.71 | 53.21 | 52.59 | 55.59 | 54.62 | 57.37 | 54.10 |
| 7:00—8:00 | 85 | 63.35 | 52.23 | 57.86 | 54.19 | 59.81 | 58.14 | 63.39 | 64.36 |
| 7:00—8:00 | 86 | 67.44 | 72.23 | 75.98 | 59.28 | 64.90 | 78.81 | 82.94 | 69.45 |
| 7:00—8:00 | 87 | 67.44 | 62.79 | 68.42 | 90.00 | 94.50 | 67.05 | 72.30 | 74.08 |
| 7:00—8:00 | 88 | 67.44 | 72.23 | 75.98 | 70.66 | 75.54 | 80.00 | 83.08 | 75.00 |
| 7:00—8:00 | 89 | 67.44 | 62.79 | 68.42 | 63.49 | 68.59 | 71.00 | 74.75 | 75.00 |
| 7:00—8:00 | 90 | 67.44 | 72.00 | 75.75 | 51.00 | 52.58 | 71.50 | 74.43 | 75.00 |
| 7:00—8:00 | 91 | 67.44 | 55.00 | 58.98 | 59.00 | 63.05 | 71.00 | 74.75 | 75.00 |
| 7:00—8:00 | 92 | 23.19 | 20.00 | 21.58 | 48.50 | 53.75 | 71.50 | 74.43 | 75.00 |
| 7:00—8:00 | 93 | 31.29 | 47.00 | 51.91 | 72.00 | 77.44 | 71.00 | 74.75 | 75.00 |
| 7:00—8:00 | 94 | 57.08 | 60.50 | 62.38 | 50.50 | 52.83 | 71.50 | 74.43 | 75.00 |
| 7:00—8:00 | 95 | 64.06 | 54.00 | 59.59 | 59.00 | 61.74 | 71.00 | 74.75 | 75.00 |
| 7:00—8:00 | 96 | 15.00 | 14.00 | 14.83 | 48.00 | 53.63 | 71.50 | 74.43 | 75.00 |
| 8:00—9:00 | 97 | 30.55 | 39.50 | 44.90 | 73.00 | 79.05 | 70.00 | 75.00 | 75.00 |
| | | | | | | | | | |
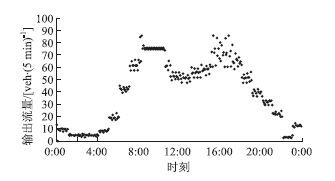
从图 6可以得出边界输出流量随时间的变化趋势:在低峰时输出流量随着交通需求的增加而变大,到早高峰8:00以后,路网达到临界饱和状态,输出流量达到最大值,状态一直持续到晚高峰结束,符合实际情况。
|
| 图 6 边界输出流量随时间变化图 Fig. 6 Boundary output traffic volume varying with time |
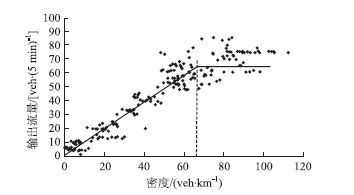
从图 7可以发现,干线输出流量与干线内累计车辆数(即密度)存在一定的关系,在密度小于65 veh/h 时,输出流量与密度呈线性相关,交通流达到临界饱和状态,个别或多个交叉口出现排队上溯现象。当密度大于65 veh/h时,交通流达到饱和状态,表现为输出流量最大。
|
| 图 7 输出流量和密度关系图 Fig. 7 Relationship between output traffic volume,density |
由上述分析可见,宏观基本图能清楚地描述干线从通畅到拥挤直至拥堵的全过程。由此可见,可以利用宏观基本图来确定路网车辆总数,使其不会导致网络交通到达锁死状态,同时,确保网络车辆总数达到最大值附近。
4 结论本文利用改进后的SPM模型快速准确地追踪了过饱和交叉口的动态排队过程,并以此得到了交通需求不断变化情况下的路网输出流量和累积车辆数。利用该数据,得出输出流量和累积车辆数之间存在确定的关系,验证了宏观基本图的存在性,为后续宏观基本图的应用提供了一定的理论基础。
| [1] | KIMBER R, HOLLIS E. Traffic Queues and Delays at Road Junctions[R]. Berkshire: Transport and Road Research Laboratory, 1979. |
| [2] | NEWELL G F. Applications of Queuing Theory[M]. New York: Chapman and Hall, 1982. |
| [3] | MAY A D. Traffic Flow Fundamentals[M]. New Jersey: Prentice-Hall, Inc, 1990. |
| [4] | DAGANZO C F. Fundamentals of Transportation and Traffic Operations[M]. Oxford:Pergamon Press, 1997. |
| [5] | MICHALOPOULOS P G, STEPHANOPOULOS G. Oversaturated Signal Systems with Queue Length Constraints[J]. |
| [6] | STEPHANOPOULOS G, MICHALOPOULOS P G, STEPHANOPOULOS G. Modelling and Analysis of Traffic Queue Dynamics at Signalized Intersections[J]. |
| [7] | 隽志才,魏丽英,李江. 信号交叉口排队长度宏观模拟的自适应分析法[J]. 中国公路学报,2000,13(1): 77-80. JUAN Zhi-cai, WEI Li-ying, LI Jiang. An Adaptive Macro-simulation Method on Queuing Length at Signalized Intersection[J]. China Journal of Highway and Transport, 2000, 13(1):77-80. |
| [8] | WU X, LIU H X. A Shockwave Profile Model for Traffic Flow on Congested Urban Arterials[J]. |
| [9] | 王殿海,付凤杰,蔡正义,等. 基于排队最远点约束的最大周期时长优化方法[J]. 华南理工大学学报:自然科学版,2014,42(5):67-74. WANG Dian-hai, FU Feng-jie, CAI Zheng-yi, et al. Optimization Method of Maximum Cycle Length Based on Back of Queue[J]. Journal of South China University of Technology: Natural Science Edition,2014,42(5):67-74. |
| [10] | SMEED R J. The Road Capacity of City Centers[J]. Highway Research Record, 1967(169):22-29. |
| [11] | HERMAN R, PRIGOGINE I. A Two-fluid Approach to Town Traffic[J]. |
| [12] | DAGANZO C F. Urban Gridlock: Macroscopic Modeling and Mitigation Approaches[J]. |
| [13] | GEROLIMINIS N, DAGANZO C F. Macroscopic Modeling of Traffic in Cities[C]//Transportation Research Board 86th Annual Meeting. Washington, D.C.: TRB, 2007. |
| [14] | 姬杨蓓蓓. 基于仿真实验验证宏观基本图的存在性[J]. 武汉理工大学学报: 交通科学与工程版,2013,37(5):929-933. JIYANG Bei-bei. Existence Verification of Macroscopic Fundamental Diagram(MFD) Based on Simulation Method[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering Edition, 2013,37(5):929-933. |
| [15] | GEROLIMINIS N, SUN J. Properties of a Well-defined Macroscopic Fundamental Diagram for Urban Traffic[J]. |
| [16] | KNOOP V L, HOOGENDOORN S P, VAN LINT J W C. The Impact of Traffic Dynamics on Macroscopic Fundamental Diagram[C]//Transportation Research Board 92nd Annual Meeting. Washington, D.C.: TRB, 2013. |
| [17] | 朱琳,于雷,宋国华. 基于 MFD 的路网宏观交通状态及影响因素研究[J]. 华南理工大学学报:自然科学版, 2012, 40(11):138-146. ZHU Lin, YU Lei, SONG Guo-hua. MFD-based Investigation into Macroscopic Traffic Status of Urban Networks and Its Influencing Factors[J]. Journal of South China University of Technology: Natural Science Edition, 2012, 40(11):138-146. |
| [18] | GEROLIMINIS N, DAGANZO C F. Existence of Urban-scale Macroscopic Fundamental Diagrams: Some Experimental Findings[J]. |
| [19] | DAGANZO C F. Urban Gridlock: Macroscopic Modeling and Mitigation Approaches[J]. |
 2016, Vol. 31
2016, Vol. 31
