扩展功能
文章信息
- 王浩, 包林基, 云美萍
- WANG Hao, BAO Lin-ji, YUN Mei-ping
- 交叉口直行待行区的车辆延迟启动策略分析
- Analysis of Delayed Starting Strategy for Through Vehicles at Intersection Waiting-zone
- 公路交通科技, 2016, Vol. 31 (4): 108-112
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 108-112
- 10.3969/j.issn.1002-0268.2016.04.017
-
文章历史
- 收稿日期: 2015-05-25
2. 同济大学 交通运输工程学院, 上海 201804
2. School of Transportation Engineering, Tongji University, Shanghai 201804, China
在城市道路车流高峰时段,车道容量将会趋于饱和,为了增加车道容量,可以考虑将车道的停车线提前,在交叉口内部设置机动车待行区[1]。机动车待行区是提高城市道路交叉口通行能力的重要手段之一,如何合理设置并利用待行区来控制车辆通行,成为众多学者研究的目标。国内学者对机动车待行区进行了一些探索。倪颖[2]和金勇等[3]以交通流理论为基础,通过停车线法等分析了设置左转待转区对交叉口通行能力的影响;王殿海等[4]利用累计曲线及交通流理论计算出左转待转区设置的临界条件;李小帅[5]和杨明等[6]提出设置直行待行区可缓解交叉口内部各交通流对空间资源的争夺。基于上述理论研究,国内部分城市已经设置了机动车待行区。研究表明,在有条件的路口设置左转与直行待行区,路口的通行能力平均提高8%~10%[6]。
现有的研究主要针对设置机动车待行区对交叉口通行能力的作用和影响及其设置的临界条件等,并未考虑如何合理利用机动车待行区来控制交叉口车流的通行。传统的直行待行区控制策略从异向左转绿灯开始,本向车辆立即进入直行待行区[7],这种控制策略导致了车辆停车次数增加,通过采用相应的交通诱导手段(如信息指示牌等)可抑制其增加。
因此,本文以降低直行车辆停车次数为目标,建立车辆延迟进入直行待行区的时间优化模型,根据不同的车流到达率,给出合理的待行区控制策略。结合上海市徐汇区宜山路-虹梅路交叉路口的调研数据,利用VISSIM软件分析优化后平均停车次数及延误等交通运行参数。
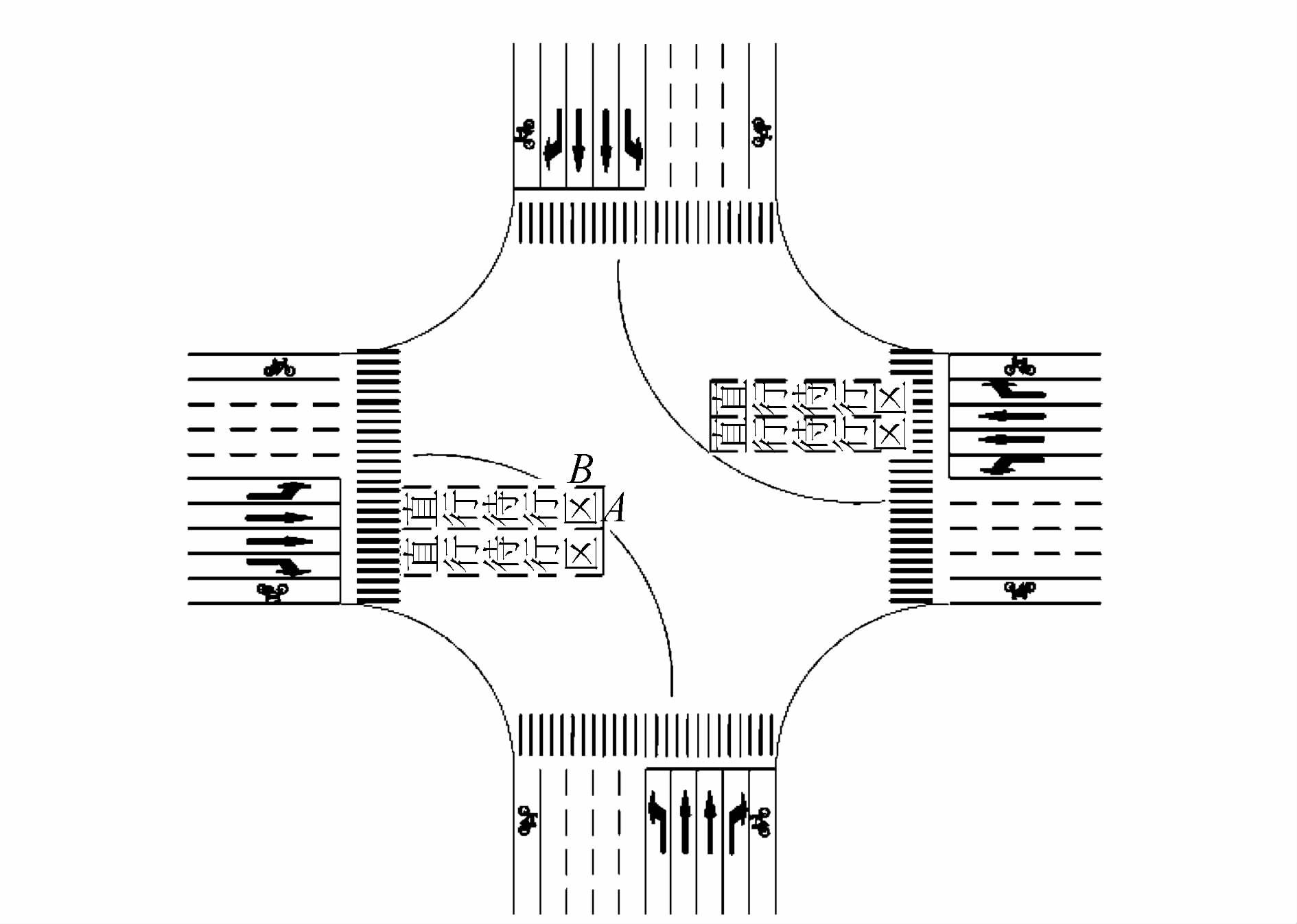
1 路段车流集散波分析 1.1 路段车辆状态描述道路车辆从上游交叉口进入下游开始到离开下游交叉口的过程如下:从车辆在道路交叉口遇到红灯后,陆续在交叉口停车线处停车结成高密度排队,形成一次集结波[8, 9];在异向左转绿灯开启后,车辆陆续驶入直行待行区,形成一次疏散波;然后车辆在待行区停车线处停车,形成二次集结波;待直行绿灯开启后,车辆离开待行区,形成二次疏散波。直行待行区如图 1所示。
|
| 图 1 直行待行区示意图 Fig. 1 Schematic diagram of through waiting-zone |
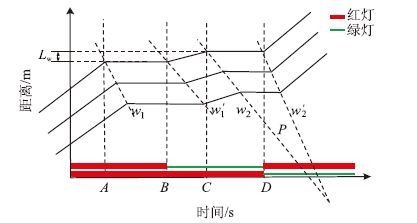
图 2是交叉口间路段车辆的时空轨迹图。每条曲线表示每辆车的状态。A点表示车辆在交叉口停车线处停车,其虚线表示车辆从运动到停止的分界,沿车队向后传播形成的集结波,其斜率即为波速w1;B点表示车辆启动,其虚线表示车辆从停止到运动的分界,沿车队向后传播形成的疏散波,其斜率即为波速w′1;C点表示车辆在待行区停车线,其虚线表示二次集结波开始形成,其斜率即为波速w2;D点表示车辆离开待行区,其虚线表示二次疏散波开始形成,其斜率即为波速w′2(下同);Lw表示待行区的长度。车辆从C点开始产生二次停车,当D点产生的疏散波开始与C点产生的集结波交汇时,车辆排队完全消散(图 3),其中由二次集结波与二次疏散波形成的区域P面积的大小表示二次停车的影响。
|
| 图 2 车辆时空轨迹图 Fig. 2 Vehicle spatio-temporal trajectories |
|
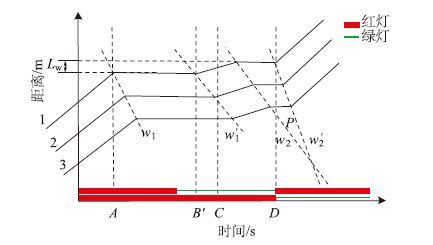
| 图 3 车辆延迟启动轨迹图 Fig. 3 Vehicle delayed starting trajectories |
机动车待行区的基本思想是车队前端车辆提前进入待行区,以增加车辆停车次数为代价为车队末端增加车辆容纳空间[10]。传统的待行区车辆控制策略是信号灯跳变为可进入待行区的相位时,车辆就立即进入待行区。当绿灯启动时,车队前端的车辆开始从待行区离开交叉口,由于排队长度较长,车队前端进入待行区时产生的第1次疏散波还未传播至车队末端,这既增加了车辆的停车次数也未能及时疏散车队末端的车辆。因此,可以结合上游车辆到达率和原始排队长度来考虑车辆延迟进入待行区的时间以减少车辆停车次数,即所谓的车辆延迟启动策略。如图 3所示,将启动点B延迟至B′,那么区域P的面积将减小,这表示停车次数与时间将减少。但同时要考虑到,延迟车队前端车辆进入待行区,亦可能造成车辆排队溢出。
2.1.1 车辆排队溢出约束在道路车辆控制过程中,要求车道不能发生溢出,以保证上游交叉口不会发生锁死。设车道长度为L,那么交叉口间路段的车辆最大排队长度Lmax必须满足:

在交通流控制中,若上游交叉口向下游释放交通流的能力大于下游交叉口的疏散能力,那么下游交叉口就会发生溢出。因此,本文假设上、下游交叉口的通行能力匹配[11],以避免不可抗力的排队溢出对系统稳定性造成破坏。
2.1.3 车辆速度均衡在车辆排队运动过程中,车辆状态可分为:停车排队、排队等待、排队前进、离开排队,其中汽车停车排队与离开排队的速度要大于排队等待与排队前进的速度。
假设停车排队与离开排队的速度相等,设为v1,排队前进的速度为v2,则有车速约束条件:v1>v2。
2.2 模型求解 2.2.1 集散波波速计算由文献[12, 13, 14]可知,集结波与疏散波(均为w)的计算公式为:
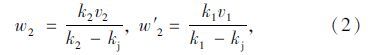
根据式(2)可计算出二次集结波w2与二次疏散波w′2:
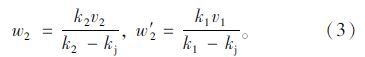
有学者通过实际交通调查数据验证发现,格林伯速度-密度模型适合描述高密度交通流状态[15],其模型如下:
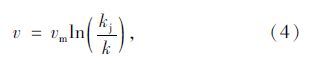
结合式(3)、式(4),则有:
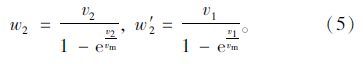
由于v1>v2,所以二次疏散波的传播速度大于二次集结波的传播速度。
2.3.2 延迟启动时间Δτ求解在交叉口直行红灯时,车辆在停车线上依次排队停车,随着红灯时间延长,排队长度不断增长,直到车辆开始进入直行待行区时,排队长度

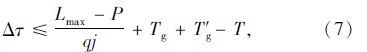
|
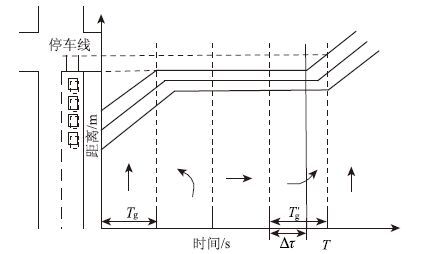
| 图 4 策略1图解 Fig. 4 Graphic of strategy 1 |
由于需要保证Δτ≤T′g-$\frac{{{L_w}}}{{{v_2}}}$,即当车辆经过待行区恰好不停车离开时有临界条件。由式(5)得,当$\frac{{{L_{\max }} - P}}{{qj}}$+Tg+T′g-T=T′g-$\frac{{{L_w}}}{{{v_2}}}$时到达率临界点,则有:
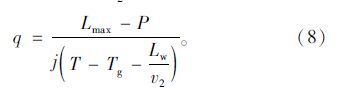
因此,可根据车辆到达率与延迟启动时间的关系分为两种控制策略:
策略1:当到达率q小于临界条件时,车道在红灯时间内不会发生排队溢出,那么可以通过延迟车辆启动时间,使车辆不停车离开交叉口,如图 4所示,即:

策略2:当到达率q大于临界条件时,应该考虑车排队溢出的情况,此时有:
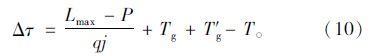
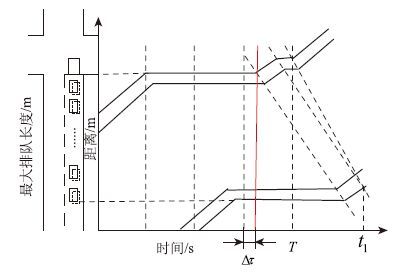
设二次疏散波与二次停车波相交的时间为t1,从图 5可知:
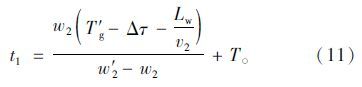
|
| 图 5 策略2图解 Fig. 5 Graphic of strategy 2 |
相交的位置H为:
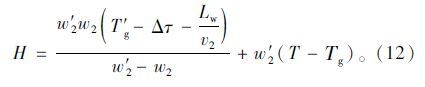
由于车辆排队不能溢出,则H≤L,可计算出到达率q的控制区间:
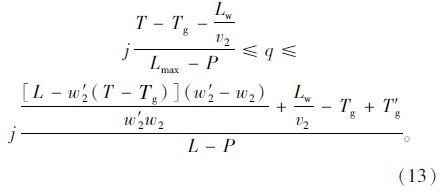
本文通过交通调查获取上海市徐汇区宜山路-虹梅路交叉路口的各项交通数据,并运用VISSIM仿真软件对上述控制策略展开实例验证,交叉口示意图以及仿真界面见图 6。图中标识A点即表示直行待行区。

|
| 图 6 交叉口示意图及仿真界面 Fig. 6 Schematic diagram of Intersection and simulation interface |
交通调查所得的交叉路口车流高峰期与平峰期的各项数据如表 1所示。
| 交通数据 | 高峰期 | 平峰期 |
| 车流到达率/(veh·h-1) | 2 400 | 900 |
| 信号周期/s | 240 | 240 |
| 本向直行绿灯/s | 53 | 53 |
| 异向左转绿灯/s | 46 | 46 |
| 初始排队长度/m | 30 | 0 |
研究假设车辆占据长度j=5 m/veh,已测得车道长度为300 m,待行区长度为20 m,车辆启动速度v1=5 m/s,车辆排队前进速度v2=2 m/s。
步骤1:由式(6)可计算到达率临界条件:q=0.31 veh/s。
步骤2:在平峰期宜用策略1控制交叉口车辆通行。由式(7)可得平峰期延迟启动时间:Δτ=36 s。
步骤3:在高峰期宜用策略2控制交叉口车辆通行。由式(4),(8),(9)可得高峰期延迟启动时间与到达率控制区间:Δτ=18 s,0.31≤q≤0.73。
3.3 仿真结果表 2为使用车流延迟启动控制策略与传统控制策略的仿真对比结果。可以看出,在平峰期通过策略1控制车辆可降低平均停车次数35.2%,在高峰期使用控制策略2可降低平均停车次数19%,并且不造成延误增加。从中可得出,随着到达率的不断增加,可延迟的时间递减,导致停车次数不断增加。
| 交通数据 | 车流高峰期 | 车流平峰期 | ||
| 传统控制策略 | 延迟启动策略 | 传统控制策略 | 延迟启动策略 | |
| 停车次数 | 2.45 | 1.98 | 1.25 | 0.81 |
| 延误/s | 45.3 | 45.9 | 18.9 | 19.1 |
本文通过分析设有直行待行区的信号交叉口停车线前的车辆集散波状态,以减少路段间车辆平均停车次数为目标,建立了车辆延迟启动模型。通过分析不同车流到达率下的车辆集散波状态,根据车流到达率的不同,给出了两种控制策略,指出了两种车辆控制策略下车流到达率的临界条件,并给出了相应的延迟时间求解过程。
经实例研究与VISSIM仿真试验,利用本文提出的策略分析得出,在不同的车辆到达率下,采用相应的控制策略可优化平均停车次数,且随着到达率的不断增加,可优化的延迟启动时间递减,从而降低停车次数的比率。文中的控制策略易于实现,且对控制左转车辆进出左转待行区也有较大参考价值。
| [1] | 左天福. 关于设置平面交叉口直行待行区的思考与实践[J]. 交通与运输,2011(增1):21-25. ZUO Tian-fu. Study and Practice on Waiting-area for Through Vehicles at Grade Intersection[J]. Traffic & Transportation,2011(S1):21-25. |
| [2] | 倪颖,李克平,徐洪峰.信号交叉口机动车左转待行区的设置研究[J].交通与运输,2006(2):32-36. NI Ying, LI Ke-ping, XU Hong-feng. Research on Waiting-area for Left-turning Vehicles in Signalized Intersections[J]. Traffic & Transportation, 2006 (2):32-36. |
| [3] | 金勇.平面交叉口转弯车流交通组织优化方法研究[D].长春:吉林大学,2006. JIN Yong. Research on Traffic Organization Optimization Methods of Turning Vehicle Flows at Grade Intersections[D].Changchun: Jilin University, 2006. |
| [4] | 王殿海, 李丽丽, 陈永恒. 机动车左弯待转区设置的临界条件[J].公路交通科技,2009, 26(11):132-135. WANG Dian-hai, LI Li-li, CHEN Yong-heng. Critical Condition for Setting Left-turn Waiting Area[J]. Journal of Highway and Transportation Research and Development, 2009,26(11):132-135. |
| [5] | 李小帅,贾顺平,孙海瑞.机动车待行区设置方法的实证研究[J]. 交通运输系统工程与信息,2011,11(增1):195-199. LI Xiao-shuai, JIA Shun-ping, SUN Hai-rui. Study on the Methods of Establishing Waiting Areas for Auto-vehicles Turning Left and Going Straight at Signalized Intersections[J]. Journal of Transportation Systems Engineering and Information Technology,2011,11(S1):195-199. |
| [6] | 杨明. 直行待行区平面交叉口交通组织及通行能力研究[D]. 武汉:武汉工业学院, 2009. YANG Ming. Research on Traffic Organization and Capacity of Intersection Straight Way Waiting-area[D]. Wuhan: Wuhan Polytechnic University,2009. |
| [7] | 周沛. 待行区交通信号控制策略及方法研究[D]. 广州:华南理工大学,2014. ZHOU Pei. Research on Traffic Signal Control Strategy and Method for Waiting Area[J].Guangzhou: South China University of Technology,2014. |
| [8] | 王进,白玉,杨晓光. 关联信号交叉口排队长度计算模型[J]. 同济大学学报,2012,40(11):1635-1640. WANG Jin, BAI Yu, YANG Xiao-guang. Queue Length Calculation Model at Adjacent Signal Intersections[J]. Journal of Tongji University,2012,40(11):1635-1640. |
| [9] | 熊烈强,王富, 李杰. 路段交通流的动力学模型及其仿真[J].中国公路学报,2006,19(2):91-94. XIONG Lie-qiang, WANG Fu, LI Jie. Dynamical Model of Traffic Flow on Segment and Its Simulation[J]. China Journal of Highway and Transport,2006,19(2):91-94. |
| [10] | 成卫, 别一鸣, 刘志远.基于机动车延误的Hook-turn交叉口信号控制方案优化方法[J].中国公路学报,2015,28(3):94-101. CHENG Wei, BIE Yi-ming, LIU Zhi-yuan. Signal Control Scheme Optimization Method for Intersection with Hook-turn Based on Motor Vehicle Delay[J]. China Journal of Highway and Transport,2015,28(3):94-101. |
| [11] | 王浩, 吴翱翔, 杨晓光. 过饱和条件下信号交叉口协调控制可靠性优化[J].公路交通科技, 2012,29(11):87-91. WANG Hao, WU Ao-xiang, YANG Xiao-guang. Reliability Optimization of Signalized Intersection Coordinated Control under Oversaturated Condition[J]. Journal of Highway and Transportation Research and Development, 2012,29(11):87-91. |
| [12] | 王殿海.交通流理论[M].北京:人民交通出版社,2002. WANG Dian-hai. Traffic Flow Theory[M]. Beijing:China Communications Press, 2002. |
| [13] | DAGANZO C F. Fundamentals of Transportation and Traffic Operations[M] . Washington D. C.:Library of Congress Cataloging-in-Publication Data,1997. |
| [14] | GARTNER N H. Monograph on Traffic Flow Theory[M]. Washington D.C.: Federal Highway Administration, 1996. |
| [15] | 姚荣涵,曲大义,王殿海. 基于运动学方程的停车波模型[J]. 吉林大学学报: 工学版, 2007,37(5):1049-1052. YAO Rong-han, Qu Da-yi, WANG Dian-hai. Stop-wave Model Based on Kinematic Equation[J]. Journal of Jilin University: Engineering and Technology Edition,2007,37(5):1049-1052. |
 2016, Vol. 31
2016, Vol. 31
