扩展功能
文章信息
- 蒋阳升, 罗孝羚, 刘媛, 姚志洪, 陈标
- JIANG Yang-sheng, LUO Xiao-ling, LIU Yuan, YAO Zhi-hong, CHEN Biao
- 公交线网空间可达性优化研究
- Study of Optimizing Transit Network Spatial Accessibility
- 公路交通科技, 2016, Vol. 31 (4): 102-107
- Journal of Highway and Transportation Research and Denelopment, 2016, Vol. 31 (4): 102-107
- 10.3969/j.issn.1002-0268.2016.04.016
-
文章历史
- 收稿日期: 2015-05-19
2. 中国建筑第八工程局有限公司上海分公司, 上海 200082
2. Shanhai Branch of China Construction Eighth Engineering Division Co., Ltd., Shanghai 200082, China
进行公交线网规划时,首先依据各种因素,率先确定区域内需要设置的公交站点和规划线路数量[1],在此基础上,确定如何将合适的站点组合到合适的线路中去,从而完成公交线路的网络布局[2]。许多学者的研究指出,空间可达性是衡量规划阶段公交线网布局合理性的最关键指标之一[3],它反映了公交线网站点与站点之间的连通性能[4]。遗憾的是现有的研究主要停留在对已经生成的公交线网站点可达性的计算与评价[3, 5, 6],对如何调整站点组合,实现公交线网空间可达性的优化,并获得对应的最佳线网布局方案缺乏深入的量化研究。本文在讨论公交线网空间可达性概念的基础上,建立公交线网可达性优化模型及相应的算法来解决上述问题。
1 相关概念与问题描述 1.1 公交线网可达性的相关概念文献[7]首度提出可达性概念,文献[6]指出公交线网可达性是站点间相互到达难易程度的描述,文献[8]提出空间可达性和时间可达性是度量公交线网可达性的主要方式,空间可达性主要用在线网的规划布局的合理性,时间可达性主要用来衡量确定线网条件下运营方案的合理性。文献[2]则指出公交线网规划对站点间距离以及单条线路长度做出的约束本质上也体现了对公交时间可达性的要求。本文主要考虑公交线网的规划布局,因此,重点考虑空间可达性的优化,而将时间可达性列为约束条件。
文献[6, 9, 10, 11]将公交可达细化为直达和换乘可达两种形式,并指出公交线网规划要以减少换乘次数为重要目标。文献[10]量化研究了公交规划中换乘次数的界限,指出换乘次数小于或等于1时其公交线网结构性能才是良好的。据此,本文将规划布局阶段的公交网络空间可达性量化理解为直达或1次换乘可达,对于超过1次换乘的到达视为不可达。
文献[12, 13, 14, 15]提出公交线网规划要以直达最大化或换乘最小化为主要目标,但公交线网规划时公交直达、换乘可达及不可达是公交线网可达性的整体描述,单一目标的优化会导致其他目标不合理。针对该问题文献[2, 9, 10]指出公交线网布局要尽量减少不可达,在此基础上实现直达最大化。据此,本文拟构建包含直达、换乘和不可达3者目标函数的加权值,作为模型目标函数。
1.2 公交线网空间可达性优化问题及求解思路描述本文所指的公交线网空间可达性优化是指在规划区域内,依据已经形成的规划站点和已知的公交线路条数,通过变化线路的站点组合,使整个公交线网空间可达性达到最佳的过程。本文将构建优化模型,设计有效算法,并通过算例进行验证分析,给出一套适合公交线网布局规划与调整的空间可达性优化计算的实用方法。
1.3 模型假设根据1.1节对相关概念的讨论分析,对模型做如下假设:
(1)假设规划区域内站点及站间距离等相关数据已知;
(2)假设公交线网规划线路数量及线路站点数量通过前期工作已经确定;
(3)假设只存在公交直达或换乘1次到达目的站点的行为才为可达,换乘两次或以上认为不可达;
(4)假设两站点存在直达和换乘可达时,即使换乘可达路径更短,出行者会选择直达出行方式。
1.4 可达性度量函数设计(1)直达可达性度量函数
站点直达可达是指出行者不需要通过换乘,可以经由某条公交线路直接从某起始公交站点到达目的站点的出行过程。
直达可达性度量函数描述如下:
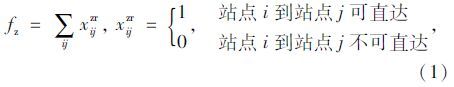
(2)换乘可达性度量函数
换乘可达是指出行者通过一条线路到达某个中间站再通过一次换乘到达另外一条线路目的地的出行过程。
换乘可达性度量函数描述如下:

(3)不可达性度量函数
不可达是除了直达及换乘可达的其他站点关系的描述。
不可达度量函数描述如下:
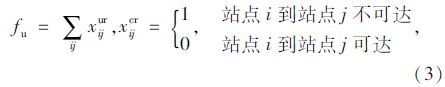
显然,直达、换乘可达及不可达对于公交线网布局规划具有不同的效果,如何衡量其对公交线网整体可达性的贡献需要合理确定它们的权重系数。如果以直达目标函数权重系数Kzr为参照标准,将其取值为1;换乘可达的系数Kcr应介于0~1之间;而目标函数要使不可达最小化。因此,不可达系数Kur取值小于0。但不可达权重系数绝对值不能过大也不能过小,过大会使目标函数值在初期过小,且进化缓慢甚至无法进化,过小则最终线网会出现不可达的情况。
1.6 公交线网空间可达性优化模型在上述分析的基础上,本文构建如下公交线网空间可达性优化模型:

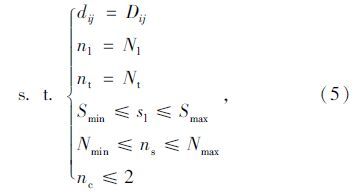
模型目标函数为直达、换乘可达及不可达子目标函数值加权求和的最大化。模型中约束分别是根据规划区域已知的规划条件和对线网规划的相关约束,即已知站点间距离、站点规划数量、规划线路条数、保证相邻站间距离约束、每条线路的站点数量约束和换乘次数约束,据此构建公交线网规划可达性优化模型。
2 基于遗传算法的可达性模型求解过程传统的可达性计算评价仅仅需要对候选方案的可达性数值进行计算,而不进行最优方案寻找,且主要是针对两站点间及单一源点。本文基于现有的可达性模型构建及计算,构建公交可达性模型,并利用遗传算法迭代优化的特点[16, 17, 18]对模型进行求解,实现公交线网空间可达性优化。
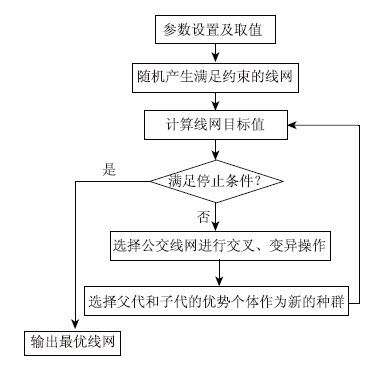
公交线网空间可达性优化遗传算法求解流程如图 1所示。
|
| 图 1 遗传算法求解流程图 Fig. 1 Flowchart of solution by genetic algorithm |
Step 1 参数设定及取值:对模型中直达目标函数系数Kzr、换乘可达目标函数系数Kcr和不可达目标函数系数Kur依据本文分析原则进行参数取值设定;通过前期工作确定规划区域站点数量nt、线路条数nl和站点间距离矩阵dij等相关数据;将交叉概率记为Pc、变异概率记为Pm、种群规模大小记为P、最大遗传代数记为G,并依据遗传算法取值原则确定取值。
Step 2 生成满足约束的公交线网:随机生成与设定的种群规模G大小一致且满足站间距离sl、线路条数nl和每条线路站点数量ns的约束公交线网。
Step 3 计算每个公交线网的目标函数值:根据优化模型(1)目标函数计算公式,计算种群的每个公交线网的目标函数值。
Step 4 对算法是否停止做出判断:如果停止,则输出优化结果;如果未停止,则进行下一步。
Step 5 选择两个公交线网进行交叉变异操作:依据选择规则和设定的交叉变异概率,选择公交线网进行相关的交叉变异操作,得到与原种群规模一致的新公交线网。
Step 6 选择新种群:对公交线网子代及其父代按目标函数值大小进行排序,取目标函数值大的作为新种群,并转至Step 3。
3 算例分析 3.1 算例求解(1)初始条件及数据:应用本模型和算法对一规划区域进行规划,首先对规划区域初始数据做出相关设定,计划在区域内规划10个公交站点,站点间距离见表 1,并对其进行标号为1~10,通过启发式算法得出计划规划线路数为6条,每条线路站点数为3~4个;对模型中目标函数的权重系数Kzr,Kcr,Kur依据本文分析的取值原则分别取1,0.7,-0.2;对遗传算法中的交叉变异Pc,Pm分别取值为0.90,0.09,种群规模及最大遗传代数分别取50,50。
| 站点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0 | 350 | 500 | 600 | 650 | 750 | 900 | 1 200 | 1 500 | 1 700 |
| 2 | 350 | 0 | 350 | 500 | 600 | 650 | 750 | 900 | 1 200 | 1 500 |
| 3 | 500 | 350 | 0 | 350 | 500 | 600 | 650 | 750 | 900 | 1 200 |
| 4 | 600 | 500 | 350 | 0 | 350 | 500 | 600 | 650 | 750 | 900 |
| 5 | 650 | 600 | 500 | 350 | 0 | 350 | 500 | 600 | 650 | 750 |
| 6 | 750 | 650 | 600 | 500 | 350 | 0 | 350 | 500 | 600 | 650 |
| 7 | 900 | 750 | 650 | 600 | 500 | 350 | 0 | 350 | 500 | 600 |
| 8 | 1 200 | 900 | 750 | 650 | 600 | 500 | 350 | 0 | 350 | 500 |
| 9 | 1 500 | 1200 | 900 | 750 | 650 | 600 | 500 | 350 | 0 | 350 |
| 10 | 1 700 | 1 500 | 1 200 | 900 | 750 | 650 | 600 | 500 | 350 | 0 |
(2)计算过程及相关数据:根据算例设定的初始条件,应用前述优化模型与遗传算法,采用Matlab编程实现优化方案的求解,取初始代线网、中间代线网及最终线网进行计算过程验证及对比。
①计算过程中第1代、第10代、第50代公交线网线路及其对应的子目标函数值,分别如表 2和表 3所示。
| 标号 | 第1代 | 第10代 | 第50代 |
| 1 | 6-2-1-3 | 8-10-7-5 | 10-9-8-4 |
| 2 | 5-6-8-4 | 3-5-6-10 | 8-7-6-2 |
| 3 | 5-1-3-4 | 9-6-5-1 | 9-6-3-1 |
| 4 | 6-7-8 | 1-5-8-7 | 3-5-7-10 |
| 5 | 8-7-5-6 | 8-4-5-6 | 8-4-5-1 |
| 6 | 6-2-1-3 | 6-2-1-3 | 4-2-1-3 |
| 代数 | 直达累加值 | 换乘累加值 | 不可达累加值 | 种群编号 |
| 第1代 | 42 | 14 | 34 | 7 |
| 第10代 | 52 | 34 | 4 | 49 |
| 第50代 | 66 | 24 | 0 | 4 |
按照上文对模型中的直达目标函数系数Kzr、换乘可达目标函数系数Kcr、不可达目标函数系数Kur的权重系数分析,取Kzr=1,Kcr=0.7,Kur=-0.2,按照式(4)可以分别得出第1代、第10代、第50代目标函数值为45,75,82.8。同样可以得到所有代的目标函数值,如表 4所示。
| 代数 | 1 | 2 | 3-4 | 5 | 6-7 | 8 | 9 | 10 |
| 最大适应度值 | 45 | 53.4 | 60.6 | 67.8 | 70.2 | 72.6 | 73.2 | 75 |
|
代数 | 11-13 | 14-15 | 16-19 | 20 | 21-25 | 26-32 | 33-50 | |
| 最大适应度值 | 77.4 | 78.6 | 79.2 | 81 | 81.6 | 82.2 | 82.8 |
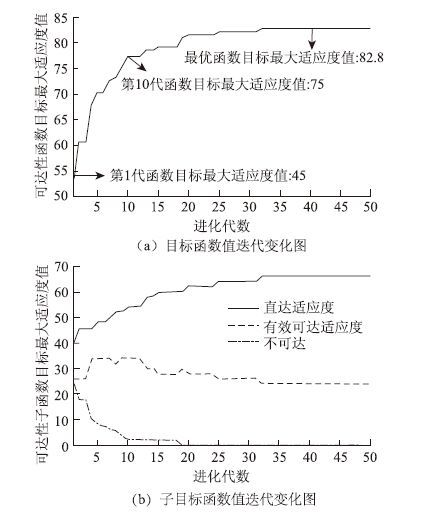
②算例目标函数值及子目标函数值迭代变化图像如图 2所示。
|
| 图 2 目标函数及子目标函数值 Fig. 2 Values of objective function and sub-objective functions |
③通过迭代最优可以得到最终优化公交线网,如表 5所示。
| 标号 | 线路 | 目标函数值 |
| 1 | 10-9-8-4 | |
| 2 | 8-7-6-2 | |
| 3 | 9-6-3-1 | 82.8 |
| 4 | 3-5-7-10 | |
| 5 | 8-4-5-1 | |
| 6 | 4-2-1-3 |
(1)迭代优化过程分析:通过表 2、表 3中第1代、第10代、第50代线网及对应目标函数值的计算,验证了计算过程的准确性,并通过线网对比,可知线网结构实现了逐步优化。
(2)可达性目标分析:通过图 2及图 3目标函数值变化图像可知,求解至第33代结果达到最大,可达性目标函数值由最初的45经过逐步优化最后达到最优为82.8。这说明通过遗传算法实现了逐步寻优,最终得到规划区域空间可达性优化方案。
(3)直达、换乘及不可达分析:在可达性目标达到最优的过程中,不可达目标函数值逐渐变小,线网可达性逐步优化。当不可达目标函数值为0时,说明整个区域通过假设的可达规则实现了任意两点都可达。在第33代时,直达目标函数值和换乘可达目标函数值的变化,表明优化线网在满足可达性的前提下优先选择直达方式的公交线网,符合公交线网直达最大化的规划原则。
(4)优化线网分析:依据可达性优化模型及遗传算法,可以得到优化线网(表 4),该公交线网方案中各子目标直达函数分别为:目标值为66,换乘目标函数值为24,不可达目标函数值为0。最终目标函数为82.8。优化线网在设定的可达性原则下,满足所有站间可达,并在此基础上形成直达最大化的线网布局。
(5)模型权重系数取值分析:模型目标函数将直达权重系数设为1作为参考标准,根据1.5节中的系数分析,本算例中换乘权重系数取0.7,不可达权重系数为-0.2,可以得到很好的计算效果。在其他规划方案中,可以根据分析的取值原则及范围结合实际情况取值。
(6)遗传算法中参数取值分析:遗传算法中主要参数有种群规模大小、最大遗传代数及交叉变异概率。种群规模过小,易出现早熟现象,种群规模过大,遗传算法计算代价较高[19];小交叉和变异率可能不能保证收敛于全局最优解,大交叉和变异率会增加迭代次数[20]。根据上述分析并结合本算例,取种群规模大小为50,交叉变异概率分别为0.90,0.09。
4 结论本文针对公交线网规划可达性优化问题,建立了以空间可达性为目标,以时间可达性为约束的优化模型。描述了公交线网规划的可达性优化模型,通过设计遗传算法对模型求解,找出了规划区域可达性最优的线路组合方式,并结合算例验证了算法的正确性和有效性。其中通过对直达、换乘可达子目标函数权重系数差异化处理,在保证可达的基础上实现了直达目标函数值最大化,使求解方案更加合理。
| [1] | 刘好德,杨晓光.基于路线优选的公交线网优化设计方法研究[J].交通与计算机,2007,25(2):14-18. LIU Hao-de,YANG Xiao-guang. Transit Routes Network Optimal Design Based on Routes Optimal Choice[J]. Computer and Communications, 2007,25(2):14-18. |
| [2] | CENDER A. Public Transit Planning and Operation[M]. London: Butterworth-Heinemann, 2007, 407-452. |
| [3] | 左盼盼.城市公共交通可达性优化模型及评价研究[D]. 兰州:兰州交通大学,2014. ZUO Pan-pan. Study on Accessibility Optimization Model and Evaluation of Urban Public Transit[D].Lanzhou: Lanzhou Jiaotong University,2014. |
| [4] | 李平华,陆玉麒.可达性研究的回顾与展望[J]. 地理科学进展,2005, 25(3):69-77. LI Ping-hua, LU Yu-qi. Review and Prospectation of Accessibility Research[J]. Progress in Geography, 2005,25(3):69-77. |
| [5] | 张学梅.基于GIS的公共交通可达性研究:以泸州市为例[D].成都:西南交通大学,2014. ZHANG Xue-mei. Research of Public Transport Accessibility on GIS: A Case Study of Luzhou[D]. Chengdu: Southwest Jiaotong University,2014. |
| [6] | 韩彪,聂伟,王卫平,等.基于公交车站的可达性度量模型[J].深圳大学学报:理工版,2013, 30(1):98-102. HAN Biao,NIE Wei,WANG Wei-ping, et al. Accessibility Measurement Model Based on Bus Stop[J].Journal of Shenzhen University: Science and Engineering Edition, 2013, 30(1):98-102. |
| [7] | HANSEN W G. How Accessibility Shapes Land-use[J]. |
| [8] | KWAN M P, MURRAY A T, OKELLY M E, et al. Recent Advances in Accessibility Research: Representation, Methodology and Applications[J]. |
| [9] | 赵巧霞,马志强,张发. 以最小换乘次数和站数为目标的公交出行算法[J].计算机应用, 2004, 24(12): 136-137,146. ZHAO Qiao-xia, MA Zhi-qiang, ZHANG Fa. Algorithms for Public Transit Trip with Minimal Transfer Times and Stops[J]. Journal of Computer Applications,2004,24(12): 136-137,146. |
| [10] | 师桂兰,邓卫,葛亮. 基于平均换乘的城市公交线网性能评价[J].洛阳大学学报,2003, 18(4):26-31. SHI Gui-lan,DENG Wei,GE Liang. Public-transit Evaluation Based on Average Transfer Times[J]. Journal of Luoyang University,2003,18(4):26-31. |
| [11] | 安健,刘好德,滕靖,等.快速公交路径优化设计模型及算法研究[J].公路交通科技,2010,27(3):147-153. AN Jian, LIU Hao-de, TENG Jing, et al. Research on Model and Algorithm of BRT Route Optimal Design[J]. Journal of Highway and Transportation Research and Development,2010,27(3):147-153. |
| [12] | 高小林.常规公交线网优化方法研究[D]. 西安:长安大学,2013. GAO Xiao-lin. Research on Conventional Transit Route Network Optimization Method[D].Xi'an:Chang'an University,2013. |
| [13] | 刘好德.公交线网优化设计理论及实现方法研究[D].上海:同济大学,2008. LIU Hao-de. Research on Bus Transit Route Network Design Theory and Implement Method[D].Shanghai: Tongji University,2008. |
| [14] | 胡开桥.公交线网评价指标体系研究[J]. 公路与汽运, 2009(6):36-41. HU Kai-qiao. Research on Evaluation Index System of Transit Network[J].Highways & Automotive Applications, 2009(6):36-41. |
| [15] | 韩传峰,胡志伟.城市公交路网性能评估的网络图方法[J].系统工程, 2003, 21(3):58-61. HAN Chuan-feng,HU Zhi-wei. The Figure Method in City Traffic Net Evaluation[J]. Systems Engineering, 2003, 21(3):58-61. |
| [16] | 卓金武. Matlab在数学建模中的应用[M].北京:北京航空航天大学出版社,2011:37-59. ZHUO Jin-wu. Application of Matlab in Mathematical Modeling[M].Beijing: Beihang University Press, 2011:37-59. |
| [17] | 葛继科,邱玉辉,吴春明,等.遗传算法研究综述[J].计算机应用研究,2008, 25(10):2912-2916. GE Ji-ke,QIU Yu-hui,WU Chun-ming, et al. Summary of Genetic Algorithms Research[J]. Application Research of Computers,2008, 25(10): 2912-2916. |
| [18] | 陈秋莲,王成栋.基于Matlab遗传算法工具箱的优化计算实现[J]. 现代电子技术,2007,30(2):124-126,129. CHEN Qiu-lian,WANG Cheng-dong. Optimization of Genetic Algorithm Toolbox Based on Matlab[J]. Modern Electronics Technique, 2007, 30(2):124-126,129. |
| [19] | 徐晓华,陈崚,陈宏建.可变种群规模的遗传算法[J].系统仿真学报, 2006, 18(4):870-872,876. XU Xiao-hua,CHEN Ling,CHEN Hong-jian. Genetic Algorithm with Variable Population Size[J]. Journal of System Simulation, 2006, 18(4):870-872,876. |
| [20] | 唐世浩,朱启疆.遗传算法中初始种群与交叉、变异率对解的影响及其解决方案[J].科技通报,2001,17(3):1-7. TANG Shi-hao, ZHU Qi-jiang. Effects of the Initial Population,Crossover and Mutation Rate to the Results of Genetic Algorithms and a Possible Solution Scheme[J]. Bulletin of Science and Technology,2001,17(3):1-7. |
 2016, Vol. 31
2016, Vol. 31
